6.5 正态分布(教学课件)__高二数学北师大(2019)选择性必修第一册(共31页PPT)
文档属性
| 名称 | 6.5 正态分布(教学课件)__高二数学北师大(2019)选择性必修第一册(共31页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 20:38:03 | ||
图片预览










文档简介
(共31张PPT)
6.5 正态分布
学习目标
1.通过实例了解正态分布密度曲线及其特点,体现逻辑推理能力(重点)
2.理解正态分布的意义,并且会用图象和函数的观点分析随机变量的分布情况,体会正态分布在实际应用中的广泛性,体现数学计算能力(重难点)
新课导入
思考下面的问题:
前面讨论了离散型随机变量,它们的取值是可以一一列举的.但在实际问题中,还有许多随机变量可以取某一区间中的所有值.例如:
1.某一自动装置无故障运转的时间X是一个随机变量,它可以取区间(0,+∞)内的所有值.
2.某种产品的寿命(使用时间)X是一个随机变量,它可以取区间[0,b]或[0,+∞)内的所有值.
怎样描述这样的随机变量的分布情况呢
新课学习
分析上面的问题:
我们先看一个例子
设X表示某产品的寿命(单位: h).假设人们对该产品有如下了解:寿命小于500h的概率为0.71,寿命在500h~800h的概率为0.22,寿命在800h~1000h的概率为0.07,如何用直观的方式呈现其概率分布
可以用直方图表示概率分布,如下图.
这个直方图的缺点是比较粗糙,没有告诉我们寿命在200h~400h的概率是多少.
新课学习
思考一下:假设人们对该产品有进一步的了解:寿命在0~200h的概率为0.2,寿命在200h~400h的概率为0.32,寿命在400h~600h的概率为0.25,寿命在600h~800h的概率为0.16,寿命在800h~1000h的概率为0.07,如何用直观的方式呈现其概率分布?
可以用直方图表示概率分布,如下图.
新课学习
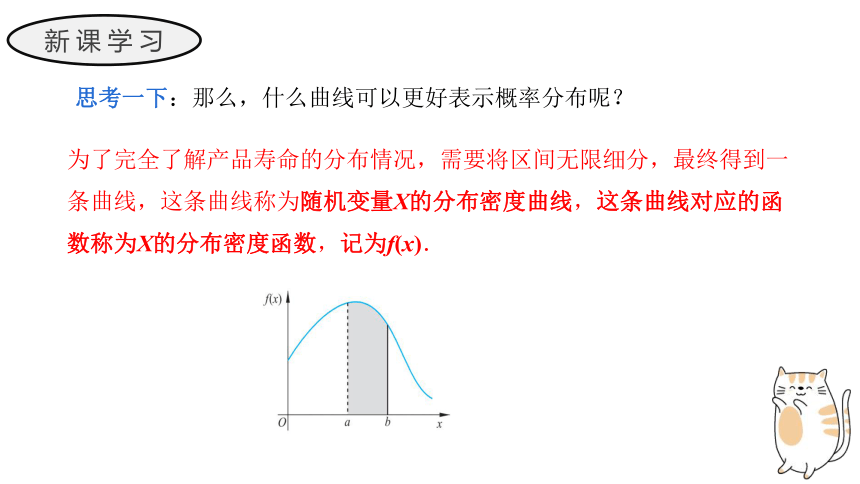
思考一下:那么,什么曲线可以更好表示概率分布呢?
为了完全了解产品寿命的分布情况,需要将区间无限细分,最终得到一条曲线,这条曲线称为随机变量X的分布密度曲线,这条曲线对应的函数称为X的分布密度函数,记为f(x).
新课学习
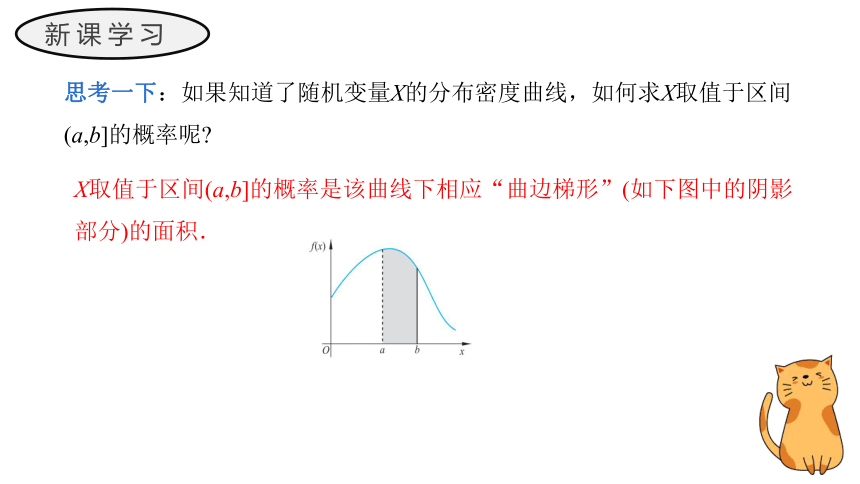
思考一下:如果知道了随机变量X的分布密度曲线,如何求X取值于区间(a,b]的概率呢
X取值于区间(a,b]的概率是该曲线下相应“曲边梯形”(如下图中的阴影部分)的面积.
新课学习
思考一下:根据上图中的分布密度的图象,思考一下分布密度有什么性质?
1.误差在0附近的概率大,远离0的概率小,误差大于0的概率与小于0的概率相同,即误差分析具有对称性
2.连续随机变量X的分布密度函数曲线一般是形状像“钟”的光滑曲线
新课学习
正态分布的概念
由误差引起的连续型随机变量其分布密度函数图象如图, 对应的分布密度函数解析式为
其中实数μ,σ(σ>0)为参数, 这一类随机变量X的分布密度 (函数) 称为正态分布密度 (函数), 简称正态分布, 对应的图象为正态分布密度曲线, 简称为正态曲线.
新课学习
思考一下:正态分布有什么特点?
1.如果一个随机变量X服从正态分布,那么对于任何一个实数a,b(a2.如果随机变量X服从正态分布,那么这个正态分布完全由参数μ,σ(σ>0)确定,记作X~N(μ,σ2),其中EX=μ,DX=σ2.
新课学习
思考一下:根据数形结合,可以发现正态曲线有哪些特点和性质?
(1)曲线在x轴的上方,与x轴不相交;(非负性)
(2)曲线是单峰的,关于直线x=μ对称;(对称性)
(3)曲线的最高点位于x=μ处;(集中性)
(4)当x<μ时,曲线上升;当x>μ时,曲线下降;当曲线向左、右两边无限延伸时,以x轴为渐近线.(单调性)
新课学习
思考一下:观察当μ或者σ一定时,正态曲线的变化情况
2.当μ一定时,曲线的形状σ由确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“高瘦”,表示总体的分布越集中.
1.当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
参数μ的含义:参数μ反映了随机变量取值的平均水平.
正态分布随机变量X在区间(μ-σ,μ+σ](σ>0)上取值的概率为阴影部分面积.
新课学习
3σ原则的概念
特别地,
P(μ-σP(μ-2σP(μ-3σ因此,随机变量X在区间(μ-σ,μ+σ],(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]上取值的概率分别为68.3%,95.4%,99.7%.
新课学习
3σ原则的概念
而随机变量X在区间(μ-3σ,μ+3σ]外取值概率只有约0.3%,通常认为这种情况在一次试验中不可能发生.因此,在实际应用中,通常认为服从正态分布X~N(μ,σ2)的随机变量X只取区间(μ-3σ,μ+3σ]之间的值,并称之为3σ原则.
新课学习
例1:根据正态曲线的函数解析式,找出其均值μ和标准差σ.
将函数解析式与正态分布密度函数的解析式对照可得:
(1)μ=0,σ =1;
(2)μ=1,σ = .
新课学习
例2:某设备在正常运行时,产品的质量服从正态分布,其参数分别为:μ=500g,σ=lg.为了检查设备运行是否正常,质量检查员需要随机地抽取产品,测量其质量.当检查员随机地抽取一个产品,测得其质量为504 g时,他立即要求停止生产,检查设备,他的决定是否有道理
检查员是有道理的,理由如下:
当该设备正常运行,产品的质量服从正态分布,其参数分别为μ=500 g,σ=1 g,所以根据正态分布的性质可知产品的质量在区间(μ-3σ,μ+3σ],即(497,503]之间的概率约为99.7%,而产品的质量超出这个范围的概率只有0.3%,这是一个几乎不可能发生的事件.
新课学习
但是,检查员随机抽取的产品为504 g,这说明设备的运行可能不正常,因此检查员的决定是有道理的.
例2:某设备在正常运行时,产品的质量服从正态分布,其参数分别为:μ=500g,σ=lg.为了检查设备运行是否正常,质量检查员需要随机地抽取产品,测量其质量.当检查员随机地抽取一个产品,测得其质量为504 g时,他立即要求停止生产,检查设备,他的决定是否有道理
新课学习
思考一下:上面的例子反映了质量控制的基本思想,那么什么是质量控制呢?
在产品生产过程中,假设生产过程是稳定的,则产品质量指标X~N(μ,σ2).
当生产正常时,产品质量指标观测值应在区间(μ-3σ,μ+3σ]内,而一旦观测值取值于区间(μ-3σ,μ+3σ]外,则属于小概率事件,由小概率事件在一次试验中几乎是不可能发生的原理,我们有理由拒绝“生产过程稳定”的假设,即认为生产过程的稳定性遭到破坏,须采取措施,以确保生产正常进行,此即为质量控制的基本思想,其实质是一个假设检验问题.
在产品质量处于稳定的条件下,可利用质量控制及时发现问题,在生产实践中,通常使用既直观又简单的控制图去实施质量控制.
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
0.75
课堂总结
1.正态分布的概念
2.3σ原则
THANK YOU
6.5 正态分布
学习目标
1.通过实例了解正态分布密度曲线及其特点,体现逻辑推理能力(重点)
2.理解正态分布的意义,并且会用图象和函数的观点分析随机变量的分布情况,体会正态分布在实际应用中的广泛性,体现数学计算能力(重难点)
新课导入
思考下面的问题:
前面讨论了离散型随机变量,它们的取值是可以一一列举的.但在实际问题中,还有许多随机变量可以取某一区间中的所有值.例如:
1.某一自动装置无故障运转的时间X是一个随机变量,它可以取区间(0,+∞)内的所有值.
2.某种产品的寿命(使用时间)X是一个随机变量,它可以取区间[0,b]或[0,+∞)内的所有值.
怎样描述这样的随机变量的分布情况呢
新课学习
分析上面的问题:
我们先看一个例子
设X表示某产品的寿命(单位: h).假设人们对该产品有如下了解:寿命小于500h的概率为0.71,寿命在500h~800h的概率为0.22,寿命在800h~1000h的概率为0.07,如何用直观的方式呈现其概率分布
可以用直方图表示概率分布,如下图.
这个直方图的缺点是比较粗糙,没有告诉我们寿命在200h~400h的概率是多少.
新课学习
思考一下:假设人们对该产品有进一步的了解:寿命在0~200h的概率为0.2,寿命在200h~400h的概率为0.32,寿命在400h~600h的概率为0.25,寿命在600h~800h的概率为0.16,寿命在800h~1000h的概率为0.07,如何用直观的方式呈现其概率分布?
可以用直方图表示概率分布,如下图.
新课学习
思考一下:那么,什么曲线可以更好表示概率分布呢?
为了完全了解产品寿命的分布情况,需要将区间无限细分,最终得到一条曲线,这条曲线称为随机变量X的分布密度曲线,这条曲线对应的函数称为X的分布密度函数,记为f(x).
新课学习
思考一下:如果知道了随机变量X的分布密度曲线,如何求X取值于区间(a,b]的概率呢
X取值于区间(a,b]的概率是该曲线下相应“曲边梯形”(如下图中的阴影部分)的面积.
新课学习
思考一下:根据上图中的分布密度的图象,思考一下分布密度有什么性质?
1.误差在0附近的概率大,远离0的概率小,误差大于0的概率与小于0的概率相同,即误差分析具有对称性
2.连续随机变量X的分布密度函数曲线一般是形状像“钟”的光滑曲线
新课学习
正态分布的概念
由误差引起的连续型随机变量其分布密度函数图象如图, 对应的分布密度函数解析式为
其中实数μ,σ(σ>0)为参数, 这一类随机变量X的分布密度 (函数) 称为正态分布密度 (函数), 简称正态分布, 对应的图象为正态分布密度曲线, 简称为正态曲线.
新课学习
思考一下:正态分布有什么特点?
1.如果一个随机变量X服从正态分布,那么对于任何一个实数a,b(a
新课学习
思考一下:根据数形结合,可以发现正态曲线有哪些特点和性质?
(1)曲线在x轴的上方,与x轴不相交;(非负性)
(2)曲线是单峰的,关于直线x=μ对称;(对称性)
(3)曲线的最高点位于x=μ处;(集中性)
(4)当x<μ时,曲线上升;当x>μ时,曲线下降;当曲线向左、右两边无限延伸时,以x轴为渐近线.(单调性)
新课学习
思考一下:观察当μ或者σ一定时,正态曲线的变化情况
2.当μ一定时,曲线的形状σ由确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“高瘦”,表示总体的分布越集中.
1.当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
参数μ的含义:参数μ反映了随机变量取值的平均水平.
正态分布随机变量X在区间(μ-σ,μ+σ](σ>0)上取值的概率为阴影部分面积.
新课学习
3σ原则的概念
特别地,
P(μ-σ
新课学习
3σ原则的概念
而随机变量X在区间(μ-3σ,μ+3σ]外取值概率只有约0.3%,通常认为这种情况在一次试验中不可能发生.因此,在实际应用中,通常认为服从正态分布X~N(μ,σ2)的随机变量X只取区间(μ-3σ,μ+3σ]之间的值,并称之为3σ原则.
新课学习
例1:根据正态曲线的函数解析式,找出其均值μ和标准差σ.
将函数解析式与正态分布密度函数的解析式对照可得:
(1)μ=0,σ =1;
(2)μ=1,σ = .
新课学习
例2:某设备在正常运行时,产品的质量服从正态分布,其参数分别为:μ=500g,σ=lg.为了检查设备运行是否正常,质量检查员需要随机地抽取产品,测量其质量.当检查员随机地抽取一个产品,测得其质量为504 g时,他立即要求停止生产,检查设备,他的决定是否有道理
检查员是有道理的,理由如下:
当该设备正常运行,产品的质量服从正态分布,其参数分别为μ=500 g,σ=1 g,所以根据正态分布的性质可知产品的质量在区间(μ-3σ,μ+3σ],即(497,503]之间的概率约为99.7%,而产品的质量超出这个范围的概率只有0.3%,这是一个几乎不可能发生的事件.
新课学习
但是,检查员随机抽取的产品为504 g,这说明设备的运行可能不正常,因此检查员的决定是有道理的.
例2:某设备在正常运行时,产品的质量服从正态分布,其参数分别为:μ=500g,σ=lg.为了检查设备运行是否正常,质量检查员需要随机地抽取产品,测量其质量.当检查员随机地抽取一个产品,测得其质量为504 g时,他立即要求停止生产,检查设备,他的决定是否有道理
新课学习
思考一下:上面的例子反映了质量控制的基本思想,那么什么是质量控制呢?
在产品生产过程中,假设生产过程是稳定的,则产品质量指标X~N(μ,σ2).
当生产正常时,产品质量指标观测值应在区间(μ-3σ,μ+3σ]内,而一旦观测值取值于区间(μ-3σ,μ+3σ]外,则属于小概率事件,由小概率事件在一次试验中几乎是不可能发生的原理,我们有理由拒绝“生产过程稳定”的假设,即认为生产过程的稳定性遭到破坏,须采取措施,以确保生产正常进行,此即为质量控制的基本思想,其实质是一个假设检验问题.
在产品质量处于稳定的条件下,可利用质量控制及时发现问题,在生产实践中,通常使用既直观又简单的控制图去实施质量控制.
课堂巩固
B
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
0.75
课堂总结
1.正态分布的概念
2.3σ原则
THANK YOU
同课章节目录
