人教版六年级下册数学四则运算和估算课件(共22张PPT)
文档属性
| 名称 | 人教版六年级下册数学四则运算和估算课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 601.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
四则运算和估算
知识点1
四则运算的意义
类别 意义 要点提示
加法 把两个或几个数合并成一个数的运算 (1)加法和减法互为逆运算,乘法和除法互为逆运算。
(2)除和除以都表示除法运算,a除以b表示a÷b,a除b表示b÷a
减法 已知两个数的和与其中的一个加数,求另一个加数的运算 乘 法 整数乘法 求几个相同加数和的简便运算 小数乘法 一个数与小数相乘,就是求这个数的十分之几、百分之几……是多少 分数乘法 一个数与分数相乘,就是求这个数的几分之几是多少 除法 已知两个因数的积与其中的一个因数,求另一个因数的运算 知识点2
四则运算的法则
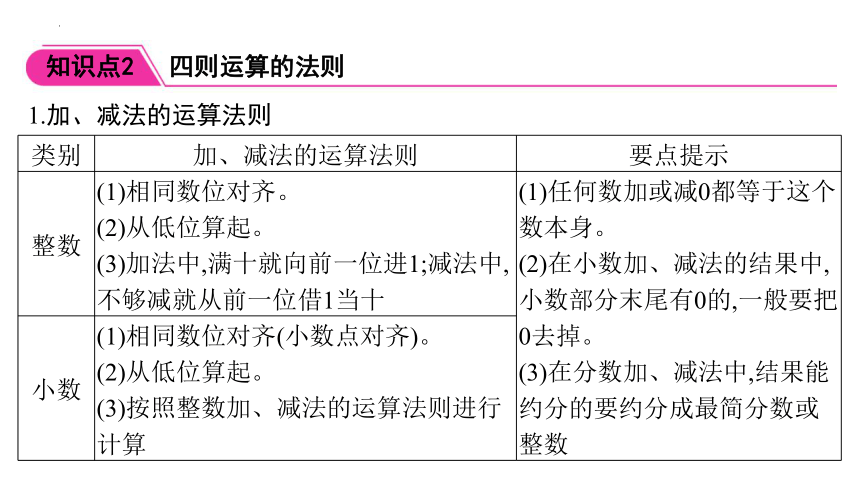
1.加、减法的运算法则
类别 加、减法的运算法则 要点提示
整数 (1)相同数位对齐。 (2)从低位算起。 (3)加法中,满十就向前一位进1;减法中,不够减就从前一位借1当十 (1)任何数加或减0都等于这个数本身。
(2)在小数加、减法的结果中,小数部分末尾有0的,一般要把0去掉。
(3)在分数加、减法中,结果能约分的要约分成最简分数或整数
小数 (1)相同数位对齐(小数点对齐)。 (2)从低位算起。 (3)按照整数加、减法的运算法则进行计算 类别 加、减法的运算法则 要点提示
分数 (1)同分母分数相加、减,分母不变,分子相加、减。 (2)异分母分数相加、减,先通分,再计算。 (3)带分数相加、减,一般先将带分数化成假分数,再将假分数相加、减 (1)任何数加或减0都等于这个数本身。
(2)在小数加、减法的结果中,小数部分末尾有0的,一般要把0去掉。
(3)在分数加、减法中,结果能约分的要约分成最简分数或整数
2.乘、除法的运算法则
(1)乘法的运算法则
类别 乘法的运算法则 要点提示
整数 ①从个位乘起,依次用第二个因数每一位上的数字去乘第一个因数。 ②用第二个因数哪一位上的数字去乘,得数的末位就和第二个因数的那一位对齐。 ③把几次乘得的数加起来。 ④因数末尾有几个0,就在乘得的数的末尾添上几个0 任何数乘0都等于0;任何数乘1都等于这个数本身
类别 乘法的运算法则 要点提示
小数 ①按照整数乘法的法则求出积。 ②看因数中一共有几位小数,就从积的右边起,数出几位(位数不够的用0补足),点上小数点。 ③积的小数部分末尾有0的,一般要把0去掉 任何数乘0都等于0;任何数乘1都等于这个数本身
分数 ①分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。 ②有整数的,把整数看作分母是1的假分数。 ③有带分数的,通常需要把带分数化成假分数 (2)除法的运算法则
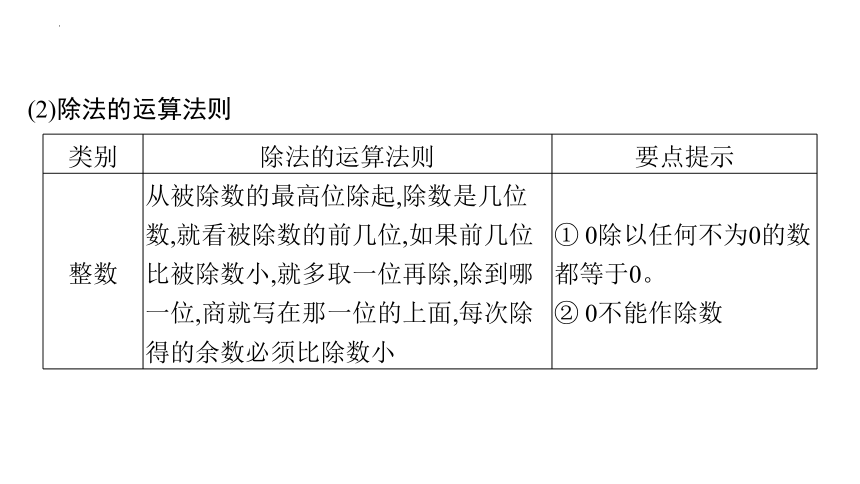
类别 除法的运算法则 要点提示
整数 从被除数的最高位除起,除数是几位数,就看被除数的前几位,如果前几位比被除数小,就多取一位再除,除到哪一位,商就写在那一位的上面,每次除得的余数必须比除数小 ① 0除以任何不为0的数都等于0。
② 0不能作除数
类别 除法的运算法则 要点提示
小数 ①当除数是整数时,按照整数除法的运算法则进行计算,商的小数点要与被除数的小数点对齐。 ②当除数是小数时,要先移动除数的小数点,把它变成整数,再把被除数的小数点向右移动相同的位数(位数不够的用0补足),最后按照除数是整数的除法运算法则进行计算 ① 0除以任何不为0的数都等于0。
② 0不能作除数
分数 ①一个数除以分数,等于乘这个分数的倒数。 ②有整数的,把整数看作分母是1的假分数。 ③有带分数的,通常需要把带分数化成假分数 知识点3
四则运算各部分之间的关系
类别 各部分之间的等量关系 要点提示
加法 加数+加数=和 一个加数=和-另一个加数 利用这些等量关系可以对加、减、乘、除法进行验算
减法 被减数-减数=差 被减数-差=减数 差+减数=被减数 乘法 因数×因数=积 一个因数=积÷另一个因数 类别 各部分之间的等量关系 要点提示
除法 没有余数的除法 被除数÷除数=商 除数×商=被除数 被除数÷商=除数 利用这些等量关系可以对加、减、乘、除法进行验算
有余数的除法 被除数÷除数=商……余数 除数×商+余数=被除数 (被除数-余数)÷商=除数 (被除数-余数)÷除数=商 知识点4
和、差、积、商的变化规律
类别 变化规律 易错警示
和 (1)如果一个加数增加(或减少)一个数,另一个加数不变,那么它们的和也增加(或减少)同一个数。 (2)如果一个加数增加(或减少)一个数,另一个加数反而减少(或增加)同一个数,那么它们的和不变 在有余数的除法中,如果被除数和除数同时乘(或除以)同一个数(0除外),那么它们的商不变,但余数也要乘(或除以)这个数
差 (1)如果被减数增加(或减少)一个数,减数不变,那么它们的差也增加(或减少)同一个数。 (2)如果被减数不变,减数增加(或减少)一个数,那么它们的差反而减少(或增加)同一个数。 (3)如果被减数和减数都增加(或减少)同一个数,那么它们的差不变 类别 变化规律 易错警示
积 (1)如果一个因数乘(或除以)一个数(0除外),另一个因数不变,那么它们的积也乘(或除以)同一个数。 (2)如果一个因数乘(或除以)一个数(0除外),另一个因数除以(或乘)同一个数,那么它们的积不变 在有余数的除法中,如果被除数和除数同时乘(或除以)同一个数(0除外),那么它们的商不变,但余数也要乘(或除以)这个数
商 (1)如果被除数乘(或除以)一个数(0除外),除数不变,那么它们的商也乘(或除以)同一个数。 (2)如果被除数不变,除数乘(或除以)一个数(0除外),那么它们的商除以(或乘)同一个数。 (3)如果被除数和除数都乘(或除以)同一个数(0除外),那么它们的商不变 知识点5
估算
估算时根据实际问题的需要,按照近似值的取值方法与加、减、乘、除法的计算方法,粗略地口算出结果。估算的结果要用“≈”连接,通常有两种估算方法,即大估法(进一法)和小估法(去尾法)。
用竖式计算。
考 点
四则运算的法则(★★★★☆)
1
例1
54×25= 840÷7= 15.8+3.9=
1350
120
19.7
18.7-9.8= 3.48×2.7= 382.5÷45=
8.9
9.396
8.5
【分析】54×25按照整数乘法的运算法则进行计算;840÷7按照整数除法的运算法则进行计算;15.8+3.9按照小数加法的运算法则进行计算;18.7-9.8按照小数减法的运算法则进行计算;3.48×2.7按照小数乘法的运算法则进行计算;382.5÷45按照小数除法的运算法则进行计算。
1.直接写出得数。
0.25+= ÷=
0÷13= 7-0.28=
5.6×= 12×30%=
268+346= 5-=
0.85
0
6.72
4.9
3.6
614
4
2.用竖式计算。
0.94×1.6= 2.1÷0.24≈ (得数保留一位小数)
1.504
8.8
1.5÷9.9= (用循环小数表示)
0.
在一道有余数的除法里,被除数、除数、商、余数的和是118,已知商是12,余数是1,被除数是( ),除数是( )。
【解析】根据“被除数=除数×商+余数”可知,被除数=除数×12+1。由“被除数、除数、商、余数的和是118”列出等量关系“被除数+除数+商+余数=118”,即除数×12+1+除数+12+1=118,解得除数=8,则被除数=8×12+1=97。
考 点
四则运算各部分之间的关系(★★★☆☆)
2
例2
97
8
3.在一道减法算式中,被减数、减数、差的和是390,被减数是( )。
4.小宇计算一道乘法算式时,把其中一个乘数22看成了2,结果得到的积是576,正确的积是( )。
195
6336
甲数除以乙数,商6余5,如果甲、乙两数都乘10,那么商( )余( )。
【解析】在有余数的除法中,如果被除数和除数同时乘10,那么它们的商不变,但余数也要乘10。
考 点
和、差、积、商的变化规律(★★★☆☆)
3
例3
6
50
5.两个数相加,一个加数增加2.5,另一个加数减少1.8,和( )。
A.减少0.7 B.增加0.7
C.减少4.3 D.增加4.3
B
四则运算和估算
知识点1
四则运算的意义
类别 意义 要点提示
加法 把两个或几个数合并成一个数的运算 (1)加法和减法互为逆运算,乘法和除法互为逆运算。
(2)除和除以都表示除法运算,a除以b表示a÷b,a除b表示b÷a
减法 已知两个数的和与其中的一个加数,求另一个加数的运算 乘 法 整数乘法 求几个相同加数和的简便运算 小数乘法 一个数与小数相乘,就是求这个数的十分之几、百分之几……是多少 分数乘法 一个数与分数相乘,就是求这个数的几分之几是多少 除法 已知两个因数的积与其中的一个因数,求另一个因数的运算 知识点2
四则运算的法则
1.加、减法的运算法则
类别 加、减法的运算法则 要点提示
整数 (1)相同数位对齐。 (2)从低位算起。 (3)加法中,满十就向前一位进1;减法中,不够减就从前一位借1当十 (1)任何数加或减0都等于这个数本身。
(2)在小数加、减法的结果中,小数部分末尾有0的,一般要把0去掉。
(3)在分数加、减法中,结果能约分的要约分成最简分数或整数
小数 (1)相同数位对齐(小数点对齐)。 (2)从低位算起。 (3)按照整数加、减法的运算法则进行计算 类别 加、减法的运算法则 要点提示
分数 (1)同分母分数相加、减,分母不变,分子相加、减。 (2)异分母分数相加、减,先通分,再计算。 (3)带分数相加、减,一般先将带分数化成假分数,再将假分数相加、减 (1)任何数加或减0都等于这个数本身。
(2)在小数加、减法的结果中,小数部分末尾有0的,一般要把0去掉。
(3)在分数加、减法中,结果能约分的要约分成最简分数或整数
2.乘、除法的运算法则
(1)乘法的运算法则
类别 乘法的运算法则 要点提示
整数 ①从个位乘起,依次用第二个因数每一位上的数字去乘第一个因数。 ②用第二个因数哪一位上的数字去乘,得数的末位就和第二个因数的那一位对齐。 ③把几次乘得的数加起来。 ④因数末尾有几个0,就在乘得的数的末尾添上几个0 任何数乘0都等于0;任何数乘1都等于这个数本身
类别 乘法的运算法则 要点提示
小数 ①按照整数乘法的法则求出积。 ②看因数中一共有几位小数,就从积的右边起,数出几位(位数不够的用0补足),点上小数点。 ③积的小数部分末尾有0的,一般要把0去掉 任何数乘0都等于0;任何数乘1都等于这个数本身
分数 ①分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。 ②有整数的,把整数看作分母是1的假分数。 ③有带分数的,通常需要把带分数化成假分数 (2)除法的运算法则
类别 除法的运算法则 要点提示
整数 从被除数的最高位除起,除数是几位数,就看被除数的前几位,如果前几位比被除数小,就多取一位再除,除到哪一位,商就写在那一位的上面,每次除得的余数必须比除数小 ① 0除以任何不为0的数都等于0。
② 0不能作除数
类别 除法的运算法则 要点提示
小数 ①当除数是整数时,按照整数除法的运算法则进行计算,商的小数点要与被除数的小数点对齐。 ②当除数是小数时,要先移动除数的小数点,把它变成整数,再把被除数的小数点向右移动相同的位数(位数不够的用0补足),最后按照除数是整数的除法运算法则进行计算 ① 0除以任何不为0的数都等于0。
② 0不能作除数
分数 ①一个数除以分数,等于乘这个分数的倒数。 ②有整数的,把整数看作分母是1的假分数。 ③有带分数的,通常需要把带分数化成假分数 知识点3
四则运算各部分之间的关系
类别 各部分之间的等量关系 要点提示
加法 加数+加数=和 一个加数=和-另一个加数 利用这些等量关系可以对加、减、乘、除法进行验算
减法 被减数-减数=差 被减数-差=减数 差+减数=被减数 乘法 因数×因数=积 一个因数=积÷另一个因数 类别 各部分之间的等量关系 要点提示
除法 没有余数的除法 被除数÷除数=商 除数×商=被除数 被除数÷商=除数 利用这些等量关系可以对加、减、乘、除法进行验算
有余数的除法 被除数÷除数=商……余数 除数×商+余数=被除数 (被除数-余数)÷商=除数 (被除数-余数)÷除数=商 知识点4
和、差、积、商的变化规律
类别 变化规律 易错警示
和 (1)如果一个加数增加(或减少)一个数,另一个加数不变,那么它们的和也增加(或减少)同一个数。 (2)如果一个加数增加(或减少)一个数,另一个加数反而减少(或增加)同一个数,那么它们的和不变 在有余数的除法中,如果被除数和除数同时乘(或除以)同一个数(0除外),那么它们的商不变,但余数也要乘(或除以)这个数
差 (1)如果被减数增加(或减少)一个数,减数不变,那么它们的差也增加(或减少)同一个数。 (2)如果被减数不变,减数增加(或减少)一个数,那么它们的差反而减少(或增加)同一个数。 (3)如果被减数和减数都增加(或减少)同一个数,那么它们的差不变 类别 变化规律 易错警示
积 (1)如果一个因数乘(或除以)一个数(0除外),另一个因数不变,那么它们的积也乘(或除以)同一个数。 (2)如果一个因数乘(或除以)一个数(0除外),另一个因数除以(或乘)同一个数,那么它们的积不变 在有余数的除法中,如果被除数和除数同时乘(或除以)同一个数(0除外),那么它们的商不变,但余数也要乘(或除以)这个数
商 (1)如果被除数乘(或除以)一个数(0除外),除数不变,那么它们的商也乘(或除以)同一个数。 (2)如果被除数不变,除数乘(或除以)一个数(0除外),那么它们的商除以(或乘)同一个数。 (3)如果被除数和除数都乘(或除以)同一个数(0除外),那么它们的商不变 知识点5
估算
估算时根据实际问题的需要,按照近似值的取值方法与加、减、乘、除法的计算方法,粗略地口算出结果。估算的结果要用“≈”连接,通常有两种估算方法,即大估法(进一法)和小估法(去尾法)。
用竖式计算。
考 点
四则运算的法则(★★★★☆)
1
例1
54×25= 840÷7= 15.8+3.9=
1350
120
19.7
18.7-9.8= 3.48×2.7= 382.5÷45=
8.9
9.396
8.5
【分析】54×25按照整数乘法的运算法则进行计算;840÷7按照整数除法的运算法则进行计算;15.8+3.9按照小数加法的运算法则进行计算;18.7-9.8按照小数减法的运算法则进行计算;3.48×2.7按照小数乘法的运算法则进行计算;382.5÷45按照小数除法的运算法则进行计算。
1.直接写出得数。
0.25+= ÷=
0÷13= 7-0.28=
5.6×= 12×30%=
268+346= 5-=
0.85
0
6.72
4.9
3.6
614
4
2.用竖式计算。
0.94×1.6= 2.1÷0.24≈ (得数保留一位小数)
1.504
8.8
1.5÷9.9= (用循环小数表示)
0.
在一道有余数的除法里,被除数、除数、商、余数的和是118,已知商是12,余数是1,被除数是( ),除数是( )。
【解析】根据“被除数=除数×商+余数”可知,被除数=除数×12+1。由“被除数、除数、商、余数的和是118”列出等量关系“被除数+除数+商+余数=118”,即除数×12+1+除数+12+1=118,解得除数=8,则被除数=8×12+1=97。
考 点
四则运算各部分之间的关系(★★★☆☆)
2
例2
97
8
3.在一道减法算式中,被减数、减数、差的和是390,被减数是( )。
4.小宇计算一道乘法算式时,把其中一个乘数22看成了2,结果得到的积是576,正确的积是( )。
195
6336
甲数除以乙数,商6余5,如果甲、乙两数都乘10,那么商( )余( )。
【解析】在有余数的除法中,如果被除数和除数同时乘10,那么它们的商不变,但余数也要乘10。
考 点
和、差、积、商的变化规律(★★★☆☆)
3
例3
6
50
5.两个数相加,一个加数增加2.5,另一个加数减少1.8,和( )。
A.减少0.7 B.增加0.7
C.减少4.3 D.增加4.3
B
