人教版四年级下册数学数学广角--鸡兔同笼课件(共31张PPT)
文档属性
| 名称 | 人教版四年级下册数学数学广角--鸡兔同笼课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
人教版四年级数学(下)册第九单元
数学广角——鸡兔同笼
情景导入
顶上红冠戴,身披五彩衣,能测天亮时,呼得众人醒。
(猜一动物)
耳朵长、尾巴短,爱吃萝卜爱吃菜,蹦蹦跳跳真可爱。(猜一动物)
猜一猜
笼子里装有鸡和兔,从上面数,共有2个头,从下面数,共有6只脚,想一想笼子里有多少只鸡?多少只兔子?
猜对了!
大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——鸡兔同笼。
创设情境,引入新课。
今有雉兔同笼,上总有六个头,下总有十六足,问雉兔各几何?
zhì
笼子里有若干只鸡和兔,从上面数,有6个头,从下面数,有16条腿。鸡和兔各有几只?
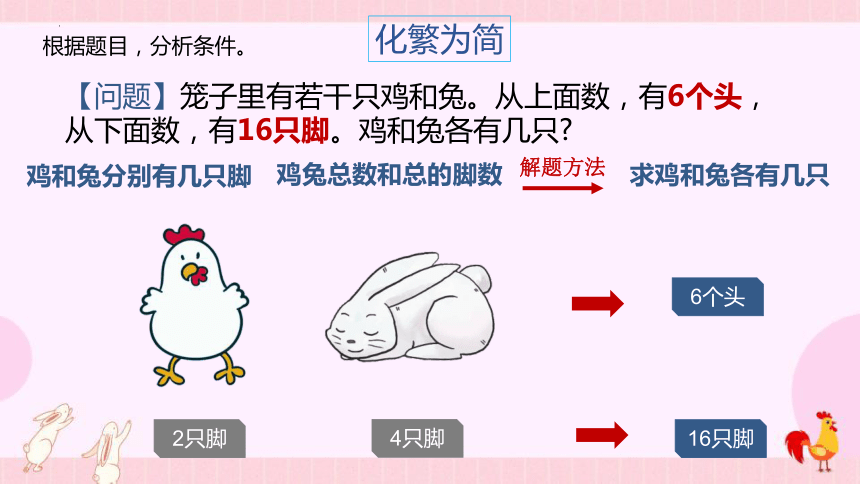
根据题目,分析条件。
6个头
16只脚
2只脚
4只脚
【问题】笼子里有若干只鸡和兔。从上面数,有6个头,从下面数,有16只脚。鸡和兔各有几只
鸡兔总数和总的脚数
求鸡和兔各有几只
解题方法
鸡和兔分别有几只脚
化繁为简
运用方法,解决例题。
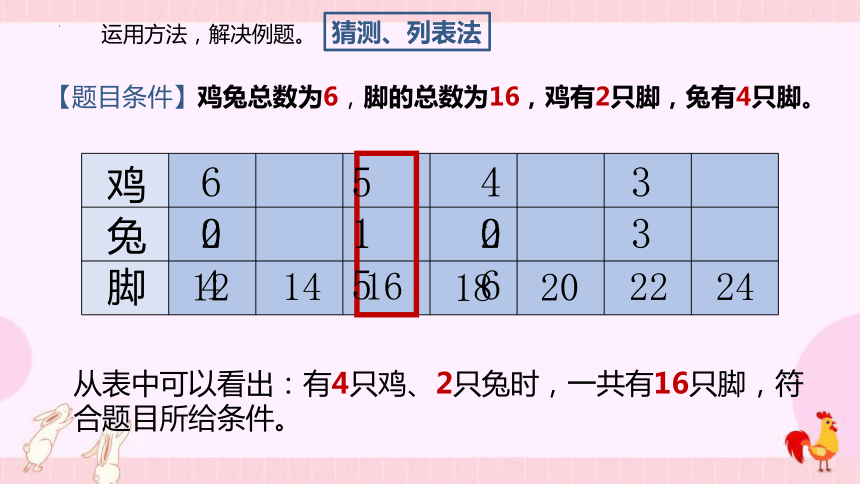
【题目条件】鸡兔总数为6,脚的总数为16,鸡有2只脚,兔有4只脚。
从表中可以看出:有4只鸡、2只兔时,一共有16只脚,符合题目所给条件。
猜测、列表法
鸡 兔 脚
6 5 4 3 2 1 0
0 1 2 3 4 5 6
12
14
16
18
20
22
24
运用方法,解决例题。
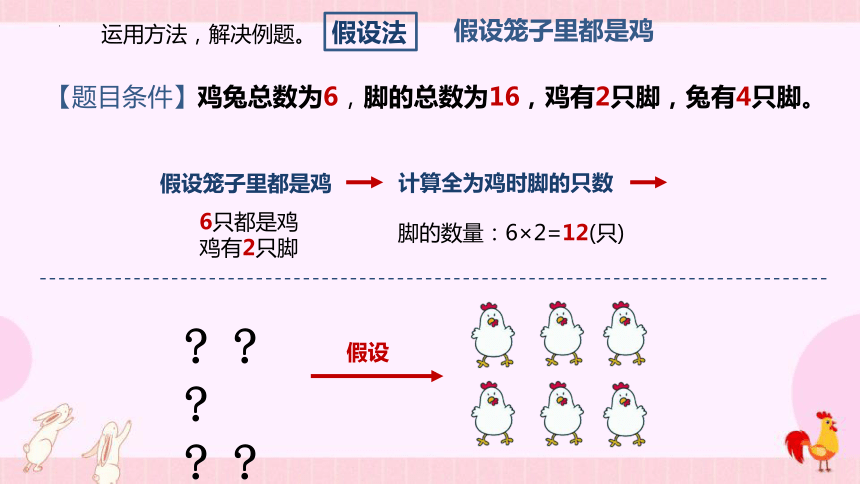
假设法
假设笼子里都是鸡
计算全为鸡时脚的只数
脚的数量:6×2=12(只)
6只都是鸡
鸡有2只脚
假设笼子里都是鸡
假设
【题目条件】鸡兔总数为6,脚的总数为16,鸡有2只脚,兔有4只脚。
运用方法,解决例题。
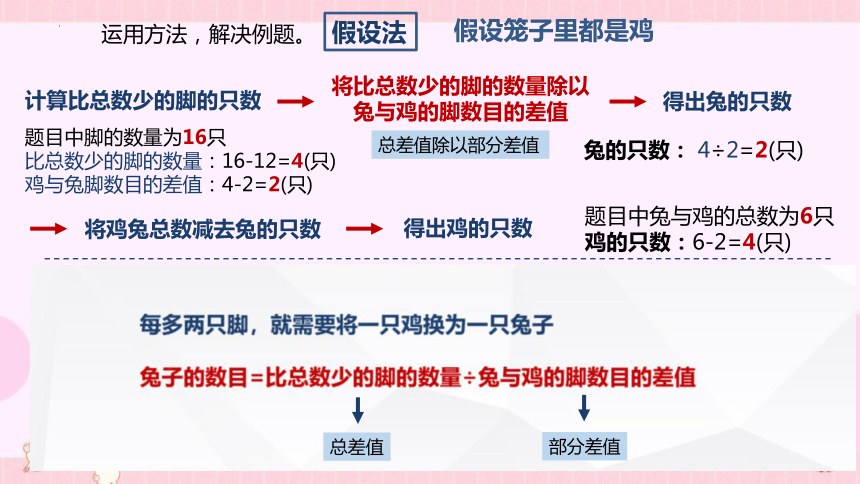
假设法
假设笼子里都是鸡
将比总数少的脚的数量除以兔与鸡的脚数目的差值
得出兔的只数
兔的只数: 4÷2=2(只)
更换
更换
6×2=12(只)
5×2+1×4=14(只)
4×2+2×4=16(只)
计算比总数少的脚的只数
题目中脚的数量为16只
比总数少的脚的数量:16-12=4(只)
鸡与兔脚数目的差值:4-2=2(只)
将鸡兔总数减去兔的只数
题目中兔与鸡的总数为6只
鸡的只数:6-2=4(只)
得出鸡的只数
总差值除以部分差值
总差值
部分差值
根据解析,规范解答。
兔的只数:( 16 – 6 × 2 )÷( 4 – 2 )
假设法
【规范解答】假设笼子里都是鸡
兔与鸡的脚数目的差值
脚的总数
全为鸡时脚的数量
鸡的只数:6 – 2
鸡兔总数
兔的只数
兔的只数
鸡的只数
=(16 – 12)÷ ( 4 – 2 )
=(16 – 12)÷ 2
= 4 ÷ 2
= 2 (只)
= 4 (只)
答:鸡有4只,兔有2只。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
从题中你能知道哪些信息?
鸡和兔共8个头,鸡和兔共有26只脚
鸡的只数×2+兔的只数×4=26
鸡 8 7 6 5 4 2 1 0
兔 0 1 2 3 4 6 7 8
脚 16 18 20 22 24 28 30 32
鸡 8 7 6 5
兔 0 1
脚 16 18
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
5
26
3
3
5
26
列表法
鸡的只数×2+兔的只数×4=26
鸡 8 7 6 5 4 3 2 1 0
兔 0 1 2 3 4 5 6 7 8
脚 16 18 20 22 24 26 28 30 32
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
将一只 换成一只 。
脚的数量增加2。
将一只 换成一只 。
脚的数量减少2。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
假设全是鸡
8×2=16(只)
26-16=10(只)
10÷2=5(只)
8-5=3(只)
(少算兔的脚)
兔:
鸡:
假设法:
4-2=2(只)
假设全是兔:
8×4=32(只)
32-26=6(只)
4-2=2(只)
鸡:6÷2=3(只)
兔:8-3=5(只)
(多算的脚是鸡的)
答:笼子里鸡有3只;兔有5只。
鸡和兔各有多少只?
我猜鸡有10只,兔有12只。
不对,那才有68条腿。
它们一共有22个头,70条腿。猜一猜吧!
2条腿
4条腿
检验:10×2+12×4=
68(条)
鸡(只)
兔(只)
腿(条)
1
21
86
2
20
84
3
19
82
4
18
80
5
17
78
6
16
76
7
15
74
8
14
72
9
13
70
它们一共有22个头,70条腿。猜一猜吧!
列表法
它们一共有22个头,70条腿。猜一猜吧!
假设这22只都是鸡,
22只鸡的腿数:22×2=44(条)
比实际少的腿数:70-44=26(条)
一只鸡比一只兔少的腿数:4-2=2(条)
拿鸡换兔,需要兔的只数:26÷2=13(只)
鸡的只数:22-13=9(只)
假设法
假设这22只都是鸡,
22×2=44(条)
70-44=26(条)
4-2=2(条)
26÷2=13(只)
22-13=9(只)
它们一共有22个头,70条腿。猜一猜吧!
假设这22只都是兔,
22只兔的腿数:22×4=88(条)
比实际多的腿数:88-70=18(条)
一只兔比一只鸡多的腿数:4-2=2(条)
拿兔换鸡,需要鸡的只数:18÷2=9(只)
兔的只数:22-9=13(只)
假设法
假设这22只都是兔,
22×4=88(条)
88-70=18(条)
4-2=2(条)
18÷2=9(只)
22-9=13(只)
列表法
假设法
你更喜欢哪种方法?为什么?
用假设法解决“鸡兔同笼”问题时,要注意假设前后的两个量之间相差的数。假设全部是其中一个量,先求出的是另一个量。
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94条腿。鸡和兔各有几只?
假设这35只都是兔。
35只兔的腿数:35×4=140(条)
比实际多的腿数:140-94=46(条)
一只兔比一只鸡多的腿数:4-2=2(条)
拿兔换鸡,需要鸡的只数:46÷2=23(只)
兔的只数:35-23=12(只)
解决课前问题
兔的只数:( – × )÷( – )
假设法
兔与鸡的脚数目的差值
脚的总数
全为鸡时脚的数量
鸡的只数:35 –12
鸡兔总数
兔的只数
兔的只数
鸡的只数
=(94 – 70)÷ ( 4 – 2 )
=(94 – 70)÷ 2
= 24 ÷ 2
= 12 (只)
= 23 (只)
答:鸡有23只,兔有12只。
运用综合算式方法,解决问题。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只
94
35
2
4
2
大船条数:( – × )÷( – )
假设法
大船小船载人数量差值
人的总数
全为小船时载人数量
大船条数
=(38 – 32)÷ ( 6 – 4 )
=(38 – 32)÷ 2
= 6 ÷ 2
= 3 (条)
38
8
4
6
4
全班共38人,共租了8条船,每条船都坐满了。大小船各租了几条?(大船6人,小船4人。)
小船条数:8 – 3
船的总数
大船条数
小船条数
= 5 (条)
答:大船3条,小船5条。
运用综合算式方法,解决问题。
随堂练习
1.池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
4条腿
2条腿
假设这23只都是龟,
23×4=92(条)
92-60=32(条)
4-2=2(条)
32÷2=16(只)
23-16=7(只)
答:龟有7只,鸭有16只。
2. 用100元钱购买下面两种洗涤液。(用列表法解答)
12元/瓶
8元/瓶
要正好花完100元,可以有几种买法,各买多少瓶?
12元的洗涤液(瓶)
8元的洗涤液(瓶)
总价
1
11
100
2
9
96
3
8
100
4
6
96
5
5
100
6
3
96
7
2
100
12元的洗涤液(瓶)
8元的洗涤液(瓶)
总价
1
11
100
2
9
96
3
8
100
4
6
96
5
5
100
6
3
96
7
2
100
要正好花完100元,可以有4种买法,分别是买。
1瓶12元的洗涤液,11瓶8元的洗涤液;
3瓶12元的洗涤液,8瓶8元的洗涤液;
5瓶12元的洗涤液,5瓶8元的洗涤液;
7瓶12元的洗涤液,2瓶8元的洗涤液。
3.有龟和鹤共40只,龟的脚和鹤的脚共112条。龟、鹤各有几只?
解:
假设全是鹤
假设全是龟
40×4=160(只)
160-112=48(只)
鹤:
48÷2=24(只)
龟:
40-24=16(只)
40×2=80(只)
112-80=32(只)
32÷2=16(只)
40-16=24(只)
鹤:
龟:
答:龟有16只,鹤有24只。
4-2=2(只)
4-2=2(只)
日本的“龟鹤算”问题就是从我国的“鸡兔同笼”问题演变来的。
课堂小结,强化记忆。
1. 猜测、列表法
2. 假设法:假设笼子里都是鸡
题目特点
解题方法
总差值除以部分差值
鸡兔总数和总的脚数
求鸡和兔各有几只
解题方法
兔与鸡的脚数目的差值
脚的总数
全为鸡时脚的数量
兔的只数
鸡兔总数
兔的只数
鸡的只数
鸡和兔分别有几只脚
再见
人教版四年级数学(下)册第九单元
数学广角——鸡兔同笼
情景导入
顶上红冠戴,身披五彩衣,能测天亮时,呼得众人醒。
(猜一动物)
耳朵长、尾巴短,爱吃萝卜爱吃菜,蹦蹦跳跳真可爱。(猜一动物)
猜一猜
笼子里装有鸡和兔,从上面数,共有2个头,从下面数,共有6只脚,想一想笼子里有多少只鸡?多少只兔子?
猜对了!
大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题——鸡兔同笼。
创设情境,引入新课。
今有雉兔同笼,上总有六个头,下总有十六足,问雉兔各几何?
zhì
笼子里有若干只鸡和兔,从上面数,有6个头,从下面数,有16条腿。鸡和兔各有几只?
根据题目,分析条件。
6个头
16只脚
2只脚
4只脚
【问题】笼子里有若干只鸡和兔。从上面数,有6个头,从下面数,有16只脚。鸡和兔各有几只
鸡兔总数和总的脚数
求鸡和兔各有几只
解题方法
鸡和兔分别有几只脚
化繁为简
运用方法,解决例题。
【题目条件】鸡兔总数为6,脚的总数为16,鸡有2只脚,兔有4只脚。
从表中可以看出:有4只鸡、2只兔时,一共有16只脚,符合题目所给条件。
猜测、列表法
鸡 兔 脚
6 5 4 3 2 1 0
0 1 2 3 4 5 6
12
14
16
18
20
22
24
运用方法,解决例题。
假设法
假设笼子里都是鸡
计算全为鸡时脚的只数
脚的数量:6×2=12(只)
6只都是鸡
鸡有2只脚
假设笼子里都是鸡
假设
【题目条件】鸡兔总数为6,脚的总数为16,鸡有2只脚,兔有4只脚。
运用方法,解决例题。
假设法
假设笼子里都是鸡
将比总数少的脚的数量除以兔与鸡的脚数目的差值
得出兔的只数
兔的只数: 4÷2=2(只)
更换
更换
6×2=12(只)
5×2+1×4=14(只)
4×2+2×4=16(只)
计算比总数少的脚的只数
题目中脚的数量为16只
比总数少的脚的数量:16-12=4(只)
鸡与兔脚数目的差值:4-2=2(只)
将鸡兔总数减去兔的只数
题目中兔与鸡的总数为6只
鸡的只数:6-2=4(只)
得出鸡的只数
总差值除以部分差值
总差值
部分差值
根据解析,规范解答。
兔的只数:( 16 – 6 × 2 )÷( 4 – 2 )
假设法
【规范解答】假设笼子里都是鸡
兔与鸡的脚数目的差值
脚的总数
全为鸡时脚的数量
鸡的只数:6 – 2
鸡兔总数
兔的只数
兔的只数
鸡的只数
=(16 – 12)÷ ( 4 – 2 )
=(16 – 12)÷ 2
= 4 ÷ 2
= 2 (只)
= 4 (只)
答:鸡有4只,兔有2只。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
从题中你能知道哪些信息?
鸡和兔共8个头,鸡和兔共有26只脚
鸡的只数×2+兔的只数×4=26
鸡 8 7 6 5 4 2 1 0
兔 0 1 2 3 4 6 7 8
脚 16 18 20 22 24 28 30 32
鸡 8 7 6 5
兔 0 1
脚 16 18
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
5
26
3
3
5
26
列表法
鸡的只数×2+兔的只数×4=26
鸡 8 7 6 5 4 3 2 1 0
兔 0 1 2 3 4 5 6 7 8
脚 16 18 20 22 24 26 28 30 32
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
将一只 换成一只 。
脚的数量增加2。
将一只 换成一只 。
脚的数量减少2。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
假设全是鸡
8×2=16(只)
26-16=10(只)
10÷2=5(只)
8-5=3(只)
(少算兔的脚)
兔:
鸡:
假设法:
4-2=2(只)
假设全是兔:
8×4=32(只)
32-26=6(只)
4-2=2(只)
鸡:6÷2=3(只)
兔:8-3=5(只)
(多算的脚是鸡的)
答:笼子里鸡有3只;兔有5只。
鸡和兔各有多少只?
我猜鸡有10只,兔有12只。
不对,那才有68条腿。
它们一共有22个头,70条腿。猜一猜吧!
2条腿
4条腿
检验:10×2+12×4=
68(条)
鸡(只)
兔(只)
腿(条)
1
21
86
2
20
84
3
19
82
4
18
80
5
17
78
6
16
76
7
15
74
8
14
72
9
13
70
它们一共有22个头,70条腿。猜一猜吧!
列表法
它们一共有22个头,70条腿。猜一猜吧!
假设这22只都是鸡,
22只鸡的腿数:22×2=44(条)
比实际少的腿数:70-44=26(条)
一只鸡比一只兔少的腿数:4-2=2(条)
拿鸡换兔,需要兔的只数:26÷2=13(只)
鸡的只数:22-13=9(只)
假设法
假设这22只都是鸡,
22×2=44(条)
70-44=26(条)
4-2=2(条)
26÷2=13(只)
22-13=9(只)
它们一共有22个头,70条腿。猜一猜吧!
假设这22只都是兔,
22只兔的腿数:22×4=88(条)
比实际多的腿数:88-70=18(条)
一只兔比一只鸡多的腿数:4-2=2(条)
拿兔换鸡,需要鸡的只数:18÷2=9(只)
兔的只数:22-9=13(只)
假设法
假设这22只都是兔,
22×4=88(条)
88-70=18(条)
4-2=2(条)
18÷2=9(只)
22-9=13(只)
列表法
假设法
你更喜欢哪种方法?为什么?
用假设法解决“鸡兔同笼”问题时,要注意假设前后的两个量之间相差的数。假设全部是其中一个量,先求出的是另一个量。
笼子里有若干只鸡和兔,从上面数,有35个头,从下面数,有94条腿。鸡和兔各有几只?
假设这35只都是兔。
35只兔的腿数:35×4=140(条)
比实际多的腿数:140-94=46(条)
一只兔比一只鸡多的腿数:4-2=2(条)
拿兔换鸡,需要鸡的只数:46÷2=23(只)
兔的只数:35-23=12(只)
解决课前问题
兔的只数:( – × )÷( – )
假设法
兔与鸡的脚数目的差值
脚的总数
全为鸡时脚的数量
鸡的只数:35 –12
鸡兔总数
兔的只数
兔的只数
鸡的只数
=(94 – 70)÷ ( 4 – 2 )
=(94 – 70)÷ 2
= 24 ÷ 2
= 12 (只)
= 23 (只)
答:鸡有23只,兔有12只。
运用综合算式方法,解决问题。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只
94
35
2
4
2
大船条数:( – × )÷( – )
假设法
大船小船载人数量差值
人的总数
全为小船时载人数量
大船条数
=(38 – 32)÷ ( 6 – 4 )
=(38 – 32)÷ 2
= 6 ÷ 2
= 3 (条)
38
8
4
6
4
全班共38人,共租了8条船,每条船都坐满了。大小船各租了几条?(大船6人,小船4人。)
小船条数:8 – 3
船的总数
大船条数
小船条数
= 5 (条)
答:大船3条,小船5条。
运用综合算式方法,解决问题。
随堂练习
1.池塘里有龟和鸭共23只,它们的腿共有60条。龟和鸭各有多少只?
4条腿
2条腿
假设这23只都是龟,
23×4=92(条)
92-60=32(条)
4-2=2(条)
32÷2=16(只)
23-16=7(只)
答:龟有7只,鸭有16只。
2. 用100元钱购买下面两种洗涤液。(用列表法解答)
12元/瓶
8元/瓶
要正好花完100元,可以有几种买法,各买多少瓶?
12元的洗涤液(瓶)
8元的洗涤液(瓶)
总价
1
11
100
2
9
96
3
8
100
4
6
96
5
5
100
6
3
96
7
2
100
12元的洗涤液(瓶)
8元的洗涤液(瓶)
总价
1
11
100
2
9
96
3
8
100
4
6
96
5
5
100
6
3
96
7
2
100
要正好花完100元,可以有4种买法,分别是买。
1瓶12元的洗涤液,11瓶8元的洗涤液;
3瓶12元的洗涤液,8瓶8元的洗涤液;
5瓶12元的洗涤液,5瓶8元的洗涤液;
7瓶12元的洗涤液,2瓶8元的洗涤液。
3.有龟和鹤共40只,龟的脚和鹤的脚共112条。龟、鹤各有几只?
解:
假设全是鹤
假设全是龟
40×4=160(只)
160-112=48(只)
鹤:
48÷2=24(只)
龟:
40-24=16(只)
40×2=80(只)
112-80=32(只)
32÷2=16(只)
40-16=24(只)
鹤:
龟:
答:龟有16只,鹤有24只。
4-2=2(只)
4-2=2(只)
日本的“龟鹤算”问题就是从我国的“鸡兔同笼”问题演变来的。
课堂小结,强化记忆。
1. 猜测、列表法
2. 假设法:假设笼子里都是鸡
题目特点
解题方法
总差值除以部分差值
鸡兔总数和总的脚数
求鸡和兔各有几只
解题方法
兔与鸡的脚数目的差值
脚的总数
全为鸡时脚的数量
兔的只数
鸡兔总数
兔的只数
鸡的只数
鸡和兔分别有几只脚
再见
