五年级暑假新课提升练第四至七单元练习检测卷(含解析)-2024-2025学年下学期小学数学北师大版
文档属性
| 名称 | 五年级暑假新课提升练第四至七单元练习检测卷(含解析)-2024-2025学年下学期小学数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 00:00:00 | ||
图片预览


文档简介
五年级暑假新课提升练第四至七单元练习检测卷(含解析)-2024-2025学年下学期小学数学北师大版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一批货物,第一次运走了吨,第二次运走了这批货物的,两次运走的货物相比,( )。
A.第一次运走的多 B.第二次运走的多
C.两次运走一样多 D.无法比较
2.下雪了!小鸭雪地画枫叶(如图),这个脚印的面积大约是( )。
A.10平方厘米 B.15平方厘米 C.20平方厘米 D.40平方厘米
3.张叔叔准备在圆形池塘周围栽树。池塘的周长是240米,如果每隔10米栽一棵,一共要栽树( )棵。
A.23 B.24 C.25 D.26
4.将60朵郁金香和36朵向日葵全部扎成花束,每束花里相同种类花的朵数都相等。这些花最多可以扎成( )束。
A.8 B.12 C.24 D.48
5.一个梯形的面积是8m2,高是0.5m,它的上底和下底的和是( )m。
A.32 B.16 C.不能计算
6.一个直角梯形的高是12厘米,如果把它的上底向一端延长3厘米就成为一个正方形,这个梯形的面积是( )平方厘米。
A.379 B.252 C.218 D.126
7.如果将的分子加9,要使分数的大小不变,它的分母应( )。
A.加9 B.加15 C.乘9 D.乘3
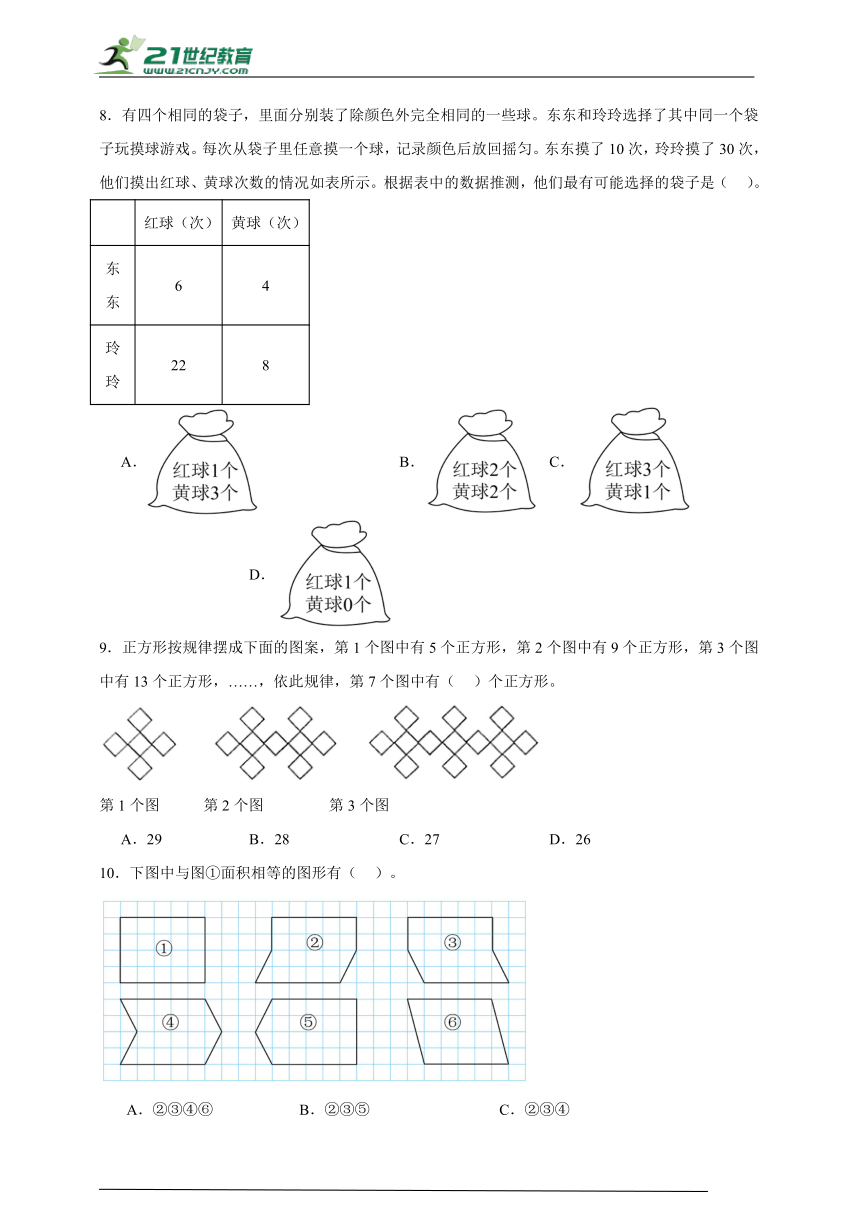
8.有四个相同的袋子,里面分别装了除颜色外完全相同的一些球。东东和玲玲选择了其中同一个袋子玩摸球游戏。每次从袋子里任意摸一个球,记录颜色后放回摇匀。东东摸了10次,玲玲摸了30次,他们摸出红球、黄球次数的情况如表所示。根据表中的数据推测,他们最有可能选择的袋子是( )。
红球(次) 黄球(次)
东东 6 4
玲玲 22 8
A. B. C. D.
9.正方形按规律摆成下面的图案,第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,依此规律,第7个图中有( )个正方形。
第1个图 第2个图 第3个图
A.29 B.28 C.27 D.26
10.下图中与图①面积相等的图形有( )。
A.②③④⑥ B.②③⑤ C.②③④
二、填空题
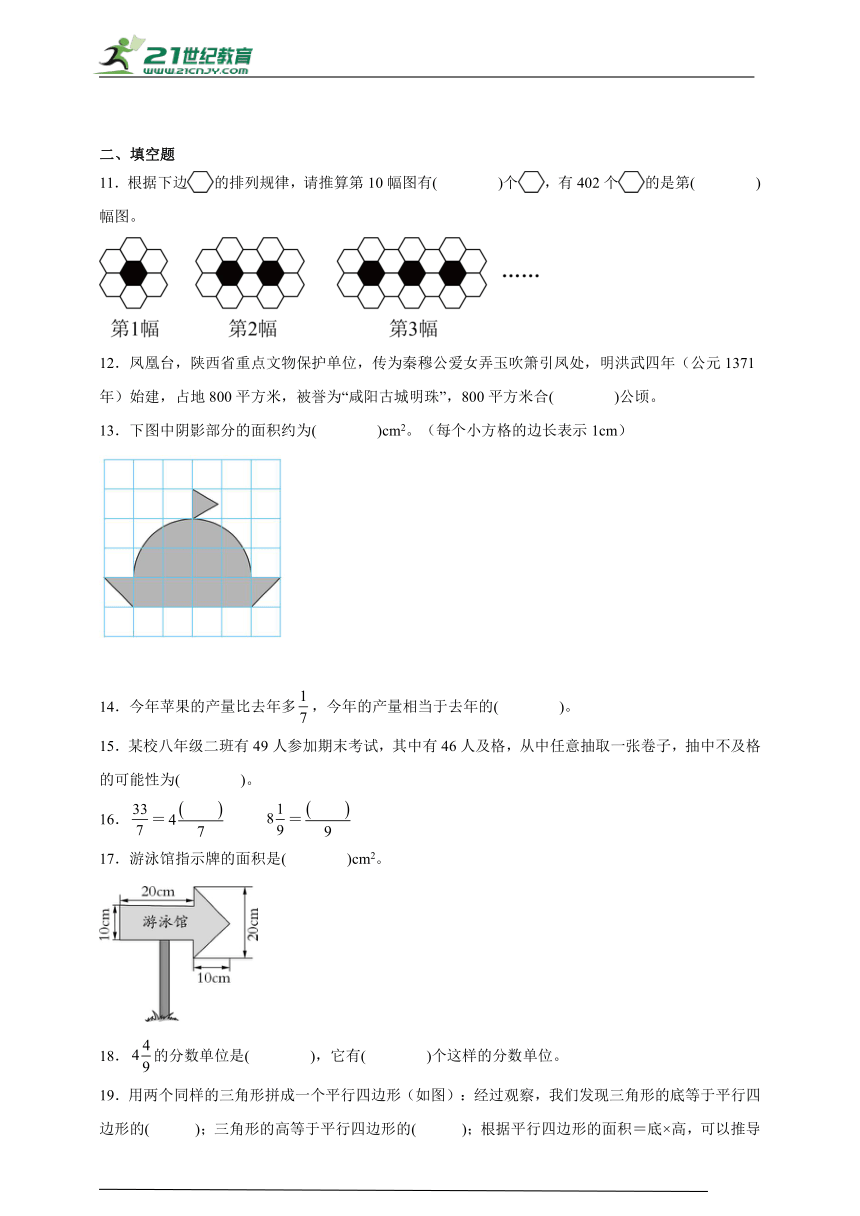
11.根据下边的排列规律,请推算第10幅图有( )个,有402个的是第( )幅图。
12.凤凰台,陕西省重点文物保护单位,传为秦穆公爱女弄玉吹箫引凤处,明洪武四年(公元1371年)始建,占地800平方米,被誉为“咸阳古城明珠”,800平方米合( )公顷。
13.下图中阴影部分的面积约为( )cm2。(每个小方格的边长表示1cm)
14.今年苹果的产量比去年多,今年的产量相当于去年的( )。
15.某校八年级二班有49人参加期末考试,其中有46人及格,从中任意抽取一张卷子,抽中不及格的可能性为( )。
16.= =
17.游泳馆指示牌的面积是( )cm2。
18.的分数单位是( ),它有( )个这样的分数单位。
19.用两个同样的三角形拼成一个平行四边形(如图):经过观察,我们发现三角形的底等于平行四边形的( );三角形的高等于平行四边形的( );根据平行四边形的面积=底×高,可以推导出三角形的面积=( )。
20.
(1)如图,在上面的括号里填假分数,在下面的括号里填带分数。
(2)分数A里面有2个,分数B的分子是7,分母是最小的合数。在上面的数轴上标出分数A和分数B。
三、判断题
21.1和这两个分数中,1更接近1。( )
22.测量较大面积的土地时,一般用公顷或平方千米作单位。( )
23.一个三角形的面积是36平方分米,高是9分米,底是4分米。( )
24.因为1÷3=,1÷3=0.333…,所以=0.333…。( )
25.把一个长方形框架拉成平行四边形后,所得图形和原图形的周长相等,面积也相等。( )
26.两个面积相等的图形的形状也一定相同。( )
27.一个口袋里装有2个红球、5个黄球、1个白球,任意摸出1个球,摸到红球的可能性最大。( )
四、计算题
28.先约分,再比较各组分数的大小。
和 和 和
29.解方程。
五、作图题
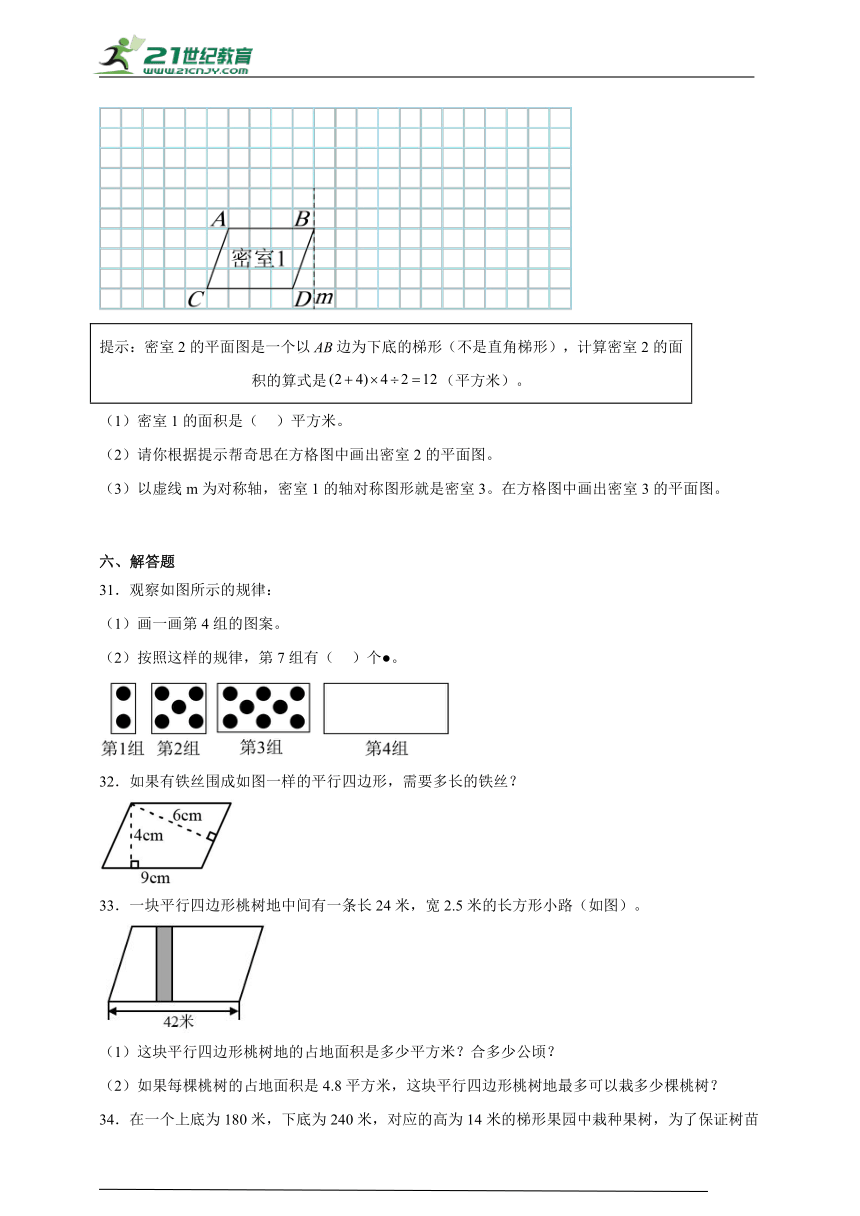
30.在数学密室游戏的复盘环节,奇思根据记忆画出了密室1的平面图。(图中每个小正方形的边长是1米)
提示:密室2的平面图是一个以边为下底的梯形(不是直角梯形),计算密室2的面积的算式是(平方米)。
(1)密室1的面积是( )平方米。
(2)请你根据提示帮奇思在方格图中画出密室2的平面图。
(3)以虚线m为对称轴,密室1的轴对称图形就是密室3。在方格图中画出密室3的平面图。
六、解答题
31.观察如图所示的规律:
(1)画一画第4组的图案。
(2)按照这样的规律,第7组有( )个●。
32.如果有铁丝围成如图一样的平行四边形,需要多长的铁丝?
33.一块平行四边形桃树地中间有一条长24米,宽2.5米的长方形小路(如图)。
(1)这块平行四边形桃树地的占地面积是多少平方米?合多少公顷?
(2)如果每棵桃树的占地面积是4.8平方米,这块平行四边形桃树地最多可以栽多少棵桃树?
34.在一个上底为180米,下底为240米,对应的高为14米的梯形果园中栽种果树,为了保证树苗成活,每棵树至少需要15平方米的种植面积,成熟后每棵果树最多可以收150千克苹果。这个果园最多可收苹果多少吨?
35.五(1)班学生在抗击新冠肺炎疫情爱心捐款活动中共捐款2000元,其中男生捐款1100元,剩下的是女生捐的。男生捐款是全班捐款总数的几分之几?女生捐款是全班捐款总数的几分之几?
36.宁宁到商店买东西,去时用了h,返回时用了h。她是去时走得快,还是返回时走得快?
《五年级暑假新课提升练第四至七单元练习检测卷(含解析)-2024-2025学年下学期小学数学北师大版》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B A D B C A A
1.B
【分析】把这批货物的重量当作单位“1”,第二次运走了这批货物的,则剩下的和第一次运走的重量一共占总重量的(1-),即,因为>,所以第一次不管运走多少吨,一定比第二次运走的少。
【详解】1-=
>
根据分析可知,一批货物,第一次运走了吨,第二次运走了这批货物的,两次运走的货物相比,第二次运走的多。
故答案为:B
【点睛】解决此题关键是弄清分数代表的是“分率”还是“具体的数量”。
2.D
【分析】数小方格的方法估算不规则图形的面积,通常是先数整格数,再数不足格数,整格数按一个面积单位计算,不足格的按半个面积单位计算。
【详解】
观察图形可知,整格4个,不足格12个,
4+12÷2
=4+6
=10(个)
2×2=4(平方厘米)
4×10=40(平方厘米)
脚印的面积大约是40平方厘米。
故答案为:D
3.B
【分析】根据“间隔数=总距离÷间距”可以求出数的间隔数,列式为:240÷5=48(个),由于在封闭图形上的植树,栽树的棵数=间隔数,所以,共植树48棵;据此解答。
【详解】根据分析可得
240÷10=24(棵)
每隔10米栽一棵,一共可栽24棵。
故答案为:B
【点睛】本题要考虑实际情况,属于在封闭图形上的植树问题,知识点是:栽树的棵数=间隔数;知识链接(沿直线上栽):栽树的棵数=间隔数-1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端)。
4.B
【分析】求这些花最多能扎多少束,就是求60和36的最大公因数,根据求最大公因数的方法:两个数的公有质因数的连乘积就是这两个数的最大公因数,据此解答。
【详解】60=2×2×3×5
36=2×2×3×3
60和36的最大公因数是:2×2×3=12;这些花最多可以扎成12束。
将60朵郁金香和36朵向日葵全部扎成花束,每束花里相同种类花的朵数都相等。这些花最多可以扎成12束。
故答案为:B
5.A
【分析】根据梯形面积公式:面积=(上底+下底)×高÷2,上底+下底=面积×2÷高,代入数据,即可解答。
【详解】8×2÷0.5
=16÷0.5
=32(m)
一个梯形的面积是8m2,高是0.5m,它的上底和下底的和是32m。
故答案为:A
【点睛】熟练掌握和灵活运用梯形面积公式是解答本题的关键。
6.D
【分析】根据题意,结合正方形的特征可知,这个梯形的下底是12厘米,上底比下底少3厘米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】上底:12-3=9(厘米)
梯形的面积是:(9+12)×12÷2
=21×12÷2
=252÷2
=126(平方厘米)
故答案为:D
7.B
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
【详解】9÷3×5
=3×5
=15
9÷3=3,分子增加了3倍,要使分数的大小不变,它的分母应增加3倍,5的3倍是15。如果将的分子加9,要使分数的大小不变,它的分母应加15。
故答案为:B
【点睛】熟练掌握分数的基本性质,是解答此题的关键。
8.C
【分析】根据可能性大小的判断方法,袋子里哪种颜色球的数量多,摸到的可能性就大;哪种颜色球的数量少,摸到的可能性就小;袋子如果只有一种颜色的球,那么一定可以摸到这种颜色的球。
【详解】从表中的数据可知,6>4,22>8,两人都是摸到红球的次数比黄球多,所以袋子中红球的数量比黄球多。
A.红球1个,黄球3个,3>1,黄球的数量多,摸到黄球的可能大,不符合题意;
B.红球2个,黄球2个,2=2,红球和黄球的数量一样多,摸到红球和黄球的可能性一样大,不符合题意;
C.红球3个,黄球1个,3>1,红球的数量多,摸到红球的可能大,符合题意;
D.红球4个,黄球0个,没有黄球,一定摸到红球,不符合题意。
故答案为:C
9.A
【分析】第一个图中有5个正方形,可以写成:4×1+1;
第二个图中有9个正方形,可以写成:4×2+1;
第三个图中有13个正方形,可以写成:4×3+1;
……
第n个图形有正方形4n+1个;据此求出第7个图中有多少个正方形。
【详解】根据分析可知,第n图中有正方形:4n+1个。
当n=7时:
4×7+1
=28+1
=29(个)
正方形按规律摆成下面的图案,第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形…,依此规律,第7个图中有29个正方形。
第一个图 第二个图 第三个图
故答案为:A
【点睛】本题考查图形变化规律,找出规律是解答本题的关键。
10.A
【分析】图①是一个长为5、宽为4的长方形;图②、图③、图④都可以分成两个完全一样的平行四边形,平行四边形的底是5、高是2,如下图;图⑤可以分成两个完全一样的梯形,梯形的上底是5、下底是6、高是2;图⑥是一个底为5、高为4的平行四边形;
然后根据长方形的面积=长×宽,平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,分别求出各图形的面积,找出哪些图形的面积与图①面积相等即可。
如图:
【详解】图①的面积:5×4=20
图②的面积:5×2×2=20,与图①面积相等;
图③的面积:5×2×2=20,与图①面积相等;
图④的面积:5×2×2=20,与图①面积相等;
图⑤的面积:
(5+6)×2÷2×2
=11×2÷2×2
=22
与图①面积不相等;
图⑥的面积:5×4=20,与图①面积相等;
所以,与图①面积相等的图形有②③④⑥。
故答案为:A
【点睛】本题考查组合图形面积的求法以及长方形、平行四边形、梯形面积公式的运用,关键是把组合图形分割成学过的图形,再用图形的面积公式求解。
11. 42 100
【分析】
第1幅图有6个。第2幅图有10个,第3幅图有14个,由此可知,下一幅图比上一幅图多4个。
第1幅图有6个,可以写成:4×1+2;
第2幅图有10个,可以写成:4×2+2;
第3幅图有14个,可以写成:4×3+2;
……
由此可知,第n幅图有(4n+2)个;当n=10时,求出有多少个;当有402个时,求出是第几幅图;(402-2)÷4解答。
【详解】
根据分析可知,第n幅图有(4n+2)个。
n=10时:
4×10+2
=40+2
=42(个)
(402-2)÷4
=400÷4
=100(幅)
第10幅图有42个,有402个的是第100幅图。
12.0.08
【分析】1公顷=10000平方米,根据高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率,据此解答即可。
【详解】800平方米=0.08公顷
【点睛】本题考查面积单位的转化和进率,高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率。
13.10.5
【分析】每个小方格的边长表示1cm,则1格的面积为1cm2。不规则图形的面积=整格数+半格数÷2(不满1格的按半格计算),据此解答。
【详解】整格数面积为6cm2,半格数的面积为9÷2=4.5cm2,所以阴影部分的面积为6+4.5=10.5cm2。
【点睛】本题主要考查不规则图形面积的估算,熟练掌握它的计算方法并灵活运用。
14./
【分析】将去年苹果的产量看作单位“1”,今年苹果的产量比去年多,今年的产量相当于去年的(1+),据此分析。
【详解】1+=
今年的产量相当于去年的。
15.
【分析】因为有49人参加期末考试,46人及格,则不及格的有3人;用不及格的人数除以总人数,结果用分数表示即可求出可能性的大小。
【详解】(49-46)÷49
=3÷49
=
抽中不及格的可能性为。
【点睛】本题主要考查可能性的大小,熟练掌握它的计算方法并灵活运用。
16.5;73
【分析】根据假分数换带分数的方法:用分子除以分母,得到的商是带分数的整数部分,分母不变,余数是分数的分子;带分数化假分数,用整数部分乘分母,加分子即可,分母不变,由此即可填空。
【详解】=
=
【点睛】本题主要考查带分数和假分数的互化,熟练掌握它们之间的关系是解题的关键。
17.300
【分析】观察图形可知,游泳馆的指示牌是由长是20cm,宽是10cm的长方形与底是20cm,高是10cm的三角形组成;根据长方形面积公式:面积=长×宽;三角形面积公式:面积=底×高÷2;代入数据,求出长方形面积和三角形面积,再相加,即可解答。
【详解】20×10+20×10÷2
=200+200÷2
=200+100
=300(cm2)
【点睛】利用长方形面积公式和三角形面积公式进行解答。
18. 40
【分析】把带分数转化成假分数,再根据分母判断分数单位是几分之一,根据分子判断有多少个这样的分数单位。
【详解】因为:==,所以:4的分数单位是,它有40个这样的分数单位。
【点睛】此题重点考查带分数化假分数的方法和对分数单位的认识。
19. 底 高 底×高÷2
【分析】观察可知,三角形的底与平行四边形的底相等,三角形的高等于平行四边形的高,又知平行四边形的面积是三角形的2倍,根据平行四边形的面积=底×高,可以推导出三角形的面积公式。
【详解】用两个同样的三角形拼成一个平行四边形(如图):经过观察,我们发现三角形的底等于平行四边形的底;三角形的高等于平行四边形的高;根据平行四边形的面积=底×高,可以推导出三角形的面积=底×高÷2。
20.(1)(2)见详解
【分析】(1)把数轴上一个单位长度看作单位“1”,把它平均分成4份,每份是,用真分数或假分数表示时,几份就是四分之几;用带分数表示时,几后面整数部分就是几,真分数按前面所述。
(2)2个是,把第一个单位长度平均分成3份,分数A表示其中的2份,据此即可在数轴上标出A;B是,根据(1)分析即可在数轴上标出B。
【详解】
【点睛】本题题是考查分数的意义。把单位“1”平均分成若干份,用分数表示,分母是平均分成的份数,分子是要表示的份数。
21.√
【分析】分别用1和这两个分数与1求差,差小的离1近。
【详解】
所以更接近1。原题说法正确。
故答案为:√
【点睛】本题主要考查分数大小的比较。
22.√
【分析】常用的面积单位有平方米、平方分米、平方厘米;其中测量土地的面积,可以用公顷作单位;计量比较大的土地面积常用公顷或平方千米作单位。
【详解】测量较大面积的土地时,一般用公顷或平方千米作单位;原题说法正确。
故答案为:√
【点睛】本题主要是考查常用的面积单位以及面积单位的选择。
23.×
【分析】三角形的面积=底×高÷2,将高是9分米,底是4分米的三角形的面积求出来,与题干作对比即可。
【详解】4×9÷2
=36÷2
=18(平方分米)
高是9分米,底是4分米的三角形的面积是18平方分米,与题干不符。
故答案为:×
24.√
【分析】如果a=b,且a=c,那么b=c,据此分析。
【详解】因为1÷3=,1÷3=0.333…,所以=0.333…,说法正确。
故答案为:√
25.×
【分析】当长方形被拉成平行四边形后,它的长和宽没变,所以周长不变,但是拉成的平行四边形的高小于长方形的宽,所以面积就变小了。据此判断。
【详解】把一个长方形活动框架拉成一个平行四边形,它的长和宽没变,所以周长不变,但是高变小了,所以面积就变小了。
因此,题干中的说法是错误的。
故答案为:×
【点睛】此题主要考查平行四边形易变形的特征,以及长方形和平行四边形的周长公式、面积公式的灵活应用。
26.×
【分析】确定一个图形面积的大小,不仅是根据图形的形状,更重要的是根据图形所占格子的多少来确定。
【详解】比如下面的正方形和长方形,都是占4个格子,它们的面积相等,形状却不同,所以原题说法错误;
故答案为:×
27.×
【分析】根据可能性知识,数量多的摸到的可能性就大,进而完成判断即可。
【详解】一个口袋里装有2个红球、5个黄球、1个白球,5>2>1,所以任意摸出1个球,摸到黄球的可能性最大。所以原题说法错误。
故答案为:×
【点睛】此题考查可能性的大小,数量多的摸到的可能性就大,根据日常生活经验判断。
28.=,=,>。
=,=,=。
=,=,<。
【分析】约分是根据分数的基本性质,一般用分子和分母的公因数(1除外)去除分数的分子和分母,通常要除到得出最简分数为止,再按照分数的大小比较的方法比较。
【详解】==,==
>
所以>
==,==
=
所以=
==,==
<
所以<
29.x=11;x=2.1;
【分析】第一个:根据等式的性质1,等式两边同时加上8,再根据等式的性质2,等式两边同时除以3即可;
第二个:根据等式的性质1,等式两边同时加上2.8x,再根据等式的性质2,等式两边同时除以6即可;
第三个:根据等式的性质1,等式两边同时加上8即可。
【详解】3x-8=25
解:3x=25+8
3x=33
x=33÷3
x=11
3.2x=12.6-2.8x
解:3.2x+2.8x=12.6
6x=12.6
x=12.6÷6
x=2.1
解:
30.(1)12
(2)(3)见详解
【分析】(1)看图可知,密室1的形状是个平行四边形,根据平行四边形的面积=底×高,列式计算即可;
(2)梯形的面积=(上底+下底)×高÷2,据此确定密室2的上底、下底和高,作图即可;
(3)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)4×3=12(平方米)
密室1的面积是12平方米。
(2)计算密室2的面积的算式是(平方米)可知,密室2的上底2米、下底4米、高4米(画法不唯一)。
(2)(3)作图如下:
31.(1)图见详解
(2)20
【分析】根据题意,第1组有2个●,第2组有2+3=5(个)●,第3组有5+3=8(个)●,后面的依次比前一组多3个●,据此解答即可。
【详解】(1)由分析可得:第1组有2个●
第2组:2+3=5(个)
第3组:5+3=8(个)
第4组:8+3=11(个)
作图如下:
(2)第5组:11+3=14(个)
第6组:14+3=17(个)
第7组:17+3=20(个)
按照这样的规律,第7组有20个●。
32.30厘米
【分析】根据平行四边形面积=底×高,求得平行四边形面积;再用平行四边形面积÷高,求得另一个底的长度,然后把两个底边相加乘2,即是需要铁丝的长度。
【详解】9×4÷6
=36÷6
=6(厘米)
(9+6)×2
=15×2
=30(厘米)
答:需要30的铁丝。
【点睛】灵活运用平行四边形面积公式是解答的关键。
33.(1)948平方米;0.0948公顷
(2)197棵
【分析】(1)观察图形可知,平行四边形的高等于长方形小路的长,这块平行四边形桃树地的占地面积,就是平行四边形面积减去小路的面积;根据平行四边形面积公式:面积=底×高;长方形面积公式:面积=长×宽,代入数据,求出桃树占地面积;1公顷=10000平方米,再化成公顷即可;
(2)用这块平行四边形桃树地的占地面积÷每颗桃树占地面积,即可求出这块平行四边形桃树地最多可以栽桃树的棵数。
【详解】42×24-24×2.5
=1008-60
=948(平方米)
948平方米=0.0948公顷
答:这块平行四边形桃树地的占地面积是948平方米,和0.0948公顷。
(2)948÷4.8≈197(棵)
答:这块平行四边形桃树地最多可以栽197棵桃树。
【点睛】熟练掌握平行四边形面积和长方形面积公式是解答本题的关键,注意单位名数的换算以及结果要用“去尾法”解答。
34.29.4吨
【分析】先根据梯形的面积=(上底+下底)×高÷2算出梯形果园的面积;再用果园的面积除以每棵树需要的种植面积可得到一共可以种植多少棵树;再用种植的棵树乘每棵果树可以收的苹果重量即可得到一共可以收多少千克苹果,最后根据1000千克=1吨,把单位换算成吨即可。
【详解】(180+240)×14÷2
=420×14÷2
=5880÷2
=2940(平方米)
2940÷15×150
=196×150
=29400(千克)
29400千克=29.4吨
答:这个果园最多可收苹果29.4吨。
【点睛】掌握梯形的面积公式及千克和吨之间的换算进率是解答本题的关键。
35.;
【分析】求男生捐款是全班捐款总数的几分之几,用男生捐款数除以全班捐款总数即可;
求女生捐款是全班捐款总数的几分之几,先用全班捐款总数减去男生捐款数,求出女生捐款数;再用女生捐款数除以全班捐款总数即可。
【详解】1100÷2000=
(2000-1100)÷2000
=900÷2000
=
答:男生捐款是全班捐款总数的,女生捐款是全班捐款总数的。
【点睛】本题考查分数与除法的关系,明确求一个数是另一个数的几分之几,用除法计算,计算结果能约分的要约成最简分数。
36.去时走得快
【分析】路程不变,只看去时用的时间少还是返回时用的时间少,用的时间少就快,据此比较h和h的大小即可。
【详解】=
=
<
所以<
答:宁宁去时走得快。
【点睛】明确走相同的路程,用的时间短的走得快是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一批货物,第一次运走了吨,第二次运走了这批货物的,两次运走的货物相比,( )。
A.第一次运走的多 B.第二次运走的多
C.两次运走一样多 D.无法比较
2.下雪了!小鸭雪地画枫叶(如图),这个脚印的面积大约是( )。
A.10平方厘米 B.15平方厘米 C.20平方厘米 D.40平方厘米
3.张叔叔准备在圆形池塘周围栽树。池塘的周长是240米,如果每隔10米栽一棵,一共要栽树( )棵。
A.23 B.24 C.25 D.26
4.将60朵郁金香和36朵向日葵全部扎成花束,每束花里相同种类花的朵数都相等。这些花最多可以扎成( )束。
A.8 B.12 C.24 D.48
5.一个梯形的面积是8m2,高是0.5m,它的上底和下底的和是( )m。
A.32 B.16 C.不能计算
6.一个直角梯形的高是12厘米,如果把它的上底向一端延长3厘米就成为一个正方形,这个梯形的面积是( )平方厘米。
A.379 B.252 C.218 D.126
7.如果将的分子加9,要使分数的大小不变,它的分母应( )。
A.加9 B.加15 C.乘9 D.乘3
8.有四个相同的袋子,里面分别装了除颜色外完全相同的一些球。东东和玲玲选择了其中同一个袋子玩摸球游戏。每次从袋子里任意摸一个球,记录颜色后放回摇匀。东东摸了10次,玲玲摸了30次,他们摸出红球、黄球次数的情况如表所示。根据表中的数据推测,他们最有可能选择的袋子是( )。
红球(次) 黄球(次)
东东 6 4
玲玲 22 8
A. B. C. D.
9.正方形按规律摆成下面的图案,第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,依此规律,第7个图中有( )个正方形。
第1个图 第2个图 第3个图
A.29 B.28 C.27 D.26
10.下图中与图①面积相等的图形有( )。
A.②③④⑥ B.②③⑤ C.②③④
二、填空题
11.根据下边的排列规律,请推算第10幅图有( )个,有402个的是第( )幅图。
12.凤凰台,陕西省重点文物保护单位,传为秦穆公爱女弄玉吹箫引凤处,明洪武四年(公元1371年)始建,占地800平方米,被誉为“咸阳古城明珠”,800平方米合( )公顷。
13.下图中阴影部分的面积约为( )cm2。(每个小方格的边长表示1cm)
14.今年苹果的产量比去年多,今年的产量相当于去年的( )。
15.某校八年级二班有49人参加期末考试,其中有46人及格,从中任意抽取一张卷子,抽中不及格的可能性为( )。
16.= =
17.游泳馆指示牌的面积是( )cm2。
18.的分数单位是( ),它有( )个这样的分数单位。
19.用两个同样的三角形拼成一个平行四边形(如图):经过观察,我们发现三角形的底等于平行四边形的( );三角形的高等于平行四边形的( );根据平行四边形的面积=底×高,可以推导出三角形的面积=( )。
20.
(1)如图,在上面的括号里填假分数,在下面的括号里填带分数。
(2)分数A里面有2个,分数B的分子是7,分母是最小的合数。在上面的数轴上标出分数A和分数B。
三、判断题
21.1和这两个分数中,1更接近1。( )
22.测量较大面积的土地时,一般用公顷或平方千米作单位。( )
23.一个三角形的面积是36平方分米,高是9分米,底是4分米。( )
24.因为1÷3=,1÷3=0.333…,所以=0.333…。( )
25.把一个长方形框架拉成平行四边形后,所得图形和原图形的周长相等,面积也相等。( )
26.两个面积相等的图形的形状也一定相同。( )
27.一个口袋里装有2个红球、5个黄球、1个白球,任意摸出1个球,摸到红球的可能性最大。( )
四、计算题
28.先约分,再比较各组分数的大小。
和 和 和
29.解方程。
五、作图题
30.在数学密室游戏的复盘环节,奇思根据记忆画出了密室1的平面图。(图中每个小正方形的边长是1米)
提示:密室2的平面图是一个以边为下底的梯形(不是直角梯形),计算密室2的面积的算式是(平方米)。
(1)密室1的面积是( )平方米。
(2)请你根据提示帮奇思在方格图中画出密室2的平面图。
(3)以虚线m为对称轴,密室1的轴对称图形就是密室3。在方格图中画出密室3的平面图。
六、解答题
31.观察如图所示的规律:
(1)画一画第4组的图案。
(2)按照这样的规律,第7组有( )个●。
32.如果有铁丝围成如图一样的平行四边形,需要多长的铁丝?
33.一块平行四边形桃树地中间有一条长24米,宽2.5米的长方形小路(如图)。
(1)这块平行四边形桃树地的占地面积是多少平方米?合多少公顷?
(2)如果每棵桃树的占地面积是4.8平方米,这块平行四边形桃树地最多可以栽多少棵桃树?
34.在一个上底为180米,下底为240米,对应的高为14米的梯形果园中栽种果树,为了保证树苗成活,每棵树至少需要15平方米的种植面积,成熟后每棵果树最多可以收150千克苹果。这个果园最多可收苹果多少吨?
35.五(1)班学生在抗击新冠肺炎疫情爱心捐款活动中共捐款2000元,其中男生捐款1100元,剩下的是女生捐的。男生捐款是全班捐款总数的几分之几?女生捐款是全班捐款总数的几分之几?
36.宁宁到商店买东西,去时用了h,返回时用了h。她是去时走得快,还是返回时走得快?
《五年级暑假新课提升练第四至七单元练习检测卷(含解析)-2024-2025学年下学期小学数学北师大版》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B A D B C A A
1.B
【分析】把这批货物的重量当作单位“1”,第二次运走了这批货物的,则剩下的和第一次运走的重量一共占总重量的(1-),即,因为>,所以第一次不管运走多少吨,一定比第二次运走的少。
【详解】1-=
>
根据分析可知,一批货物,第一次运走了吨,第二次运走了这批货物的,两次运走的货物相比,第二次运走的多。
故答案为:B
【点睛】解决此题关键是弄清分数代表的是“分率”还是“具体的数量”。
2.D
【分析】数小方格的方法估算不规则图形的面积,通常是先数整格数,再数不足格数,整格数按一个面积单位计算,不足格的按半个面积单位计算。
【详解】
观察图形可知,整格4个,不足格12个,
4+12÷2
=4+6
=10(个)
2×2=4(平方厘米)
4×10=40(平方厘米)
脚印的面积大约是40平方厘米。
故答案为:D
3.B
【分析】根据“间隔数=总距离÷间距”可以求出数的间隔数,列式为:240÷5=48(个),由于在封闭图形上的植树,栽树的棵数=间隔数,所以,共植树48棵;据此解答。
【详解】根据分析可得
240÷10=24(棵)
每隔10米栽一棵,一共可栽24棵。
故答案为:B
【点睛】本题要考虑实际情况,属于在封闭图形上的植树问题,知识点是:栽树的棵数=间隔数;知识链接(沿直线上栽):栽树的棵数=间隔数-1(两端都不栽),植树的棵数=间隔数+1(两端都栽),植树的棵数=间隔数(只栽一端)。
4.B
【分析】求这些花最多能扎多少束,就是求60和36的最大公因数,根据求最大公因数的方法:两个数的公有质因数的连乘积就是这两个数的最大公因数,据此解答。
【详解】60=2×2×3×5
36=2×2×3×3
60和36的最大公因数是:2×2×3=12;这些花最多可以扎成12束。
将60朵郁金香和36朵向日葵全部扎成花束,每束花里相同种类花的朵数都相等。这些花最多可以扎成12束。
故答案为:B
5.A
【分析】根据梯形面积公式:面积=(上底+下底)×高÷2,上底+下底=面积×2÷高,代入数据,即可解答。
【详解】8×2÷0.5
=16÷0.5
=32(m)
一个梯形的面积是8m2,高是0.5m,它的上底和下底的和是32m。
故答案为:A
【点睛】熟练掌握和灵活运用梯形面积公式是解答本题的关键。
6.D
【分析】根据题意,结合正方形的特征可知,这个梯形的下底是12厘米,上底比下底少3厘米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】上底:12-3=9(厘米)
梯形的面积是:(9+12)×12÷2
=21×12÷2
=252÷2
=126(平方厘米)
故答案为:D
7.B
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
【详解】9÷3×5
=3×5
=15
9÷3=3,分子增加了3倍,要使分数的大小不变,它的分母应增加3倍,5的3倍是15。如果将的分子加9,要使分数的大小不变,它的分母应加15。
故答案为:B
【点睛】熟练掌握分数的基本性质,是解答此题的关键。
8.C
【分析】根据可能性大小的判断方法,袋子里哪种颜色球的数量多,摸到的可能性就大;哪种颜色球的数量少,摸到的可能性就小;袋子如果只有一种颜色的球,那么一定可以摸到这种颜色的球。
【详解】从表中的数据可知,6>4,22>8,两人都是摸到红球的次数比黄球多,所以袋子中红球的数量比黄球多。
A.红球1个,黄球3个,3>1,黄球的数量多,摸到黄球的可能大,不符合题意;
B.红球2个,黄球2个,2=2,红球和黄球的数量一样多,摸到红球和黄球的可能性一样大,不符合题意;
C.红球3个,黄球1个,3>1,红球的数量多,摸到红球的可能大,符合题意;
D.红球4个,黄球0个,没有黄球,一定摸到红球,不符合题意。
故答案为:C
9.A
【分析】第一个图中有5个正方形,可以写成:4×1+1;
第二个图中有9个正方形,可以写成:4×2+1;
第三个图中有13个正方形,可以写成:4×3+1;
……
第n个图形有正方形4n+1个;据此求出第7个图中有多少个正方形。
【详解】根据分析可知,第n图中有正方形:4n+1个。
当n=7时:
4×7+1
=28+1
=29(个)
正方形按规律摆成下面的图案,第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形…,依此规律,第7个图中有29个正方形。
第一个图 第二个图 第三个图
故答案为:A
【点睛】本题考查图形变化规律,找出规律是解答本题的关键。
10.A
【分析】图①是一个长为5、宽为4的长方形;图②、图③、图④都可以分成两个完全一样的平行四边形,平行四边形的底是5、高是2,如下图;图⑤可以分成两个完全一样的梯形,梯形的上底是5、下底是6、高是2;图⑥是一个底为5、高为4的平行四边形;
然后根据长方形的面积=长×宽,平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,分别求出各图形的面积,找出哪些图形的面积与图①面积相等即可。
如图:
【详解】图①的面积:5×4=20
图②的面积:5×2×2=20,与图①面积相等;
图③的面积:5×2×2=20,与图①面积相等;
图④的面积:5×2×2=20,与图①面积相等;
图⑤的面积:
(5+6)×2÷2×2
=11×2÷2×2
=22
与图①面积不相等;
图⑥的面积:5×4=20,与图①面积相等;
所以,与图①面积相等的图形有②③④⑥。
故答案为:A
【点睛】本题考查组合图形面积的求法以及长方形、平行四边形、梯形面积公式的运用,关键是把组合图形分割成学过的图形,再用图形的面积公式求解。
11. 42 100
【分析】
第1幅图有6个。第2幅图有10个,第3幅图有14个,由此可知,下一幅图比上一幅图多4个。
第1幅图有6个,可以写成:4×1+2;
第2幅图有10个,可以写成:4×2+2;
第3幅图有14个,可以写成:4×3+2;
……
由此可知,第n幅图有(4n+2)个;当n=10时,求出有多少个;当有402个时,求出是第几幅图;(402-2)÷4解答。
【详解】
根据分析可知,第n幅图有(4n+2)个。
n=10时:
4×10+2
=40+2
=42(个)
(402-2)÷4
=400÷4
=100(幅)
第10幅图有42个,有402个的是第100幅图。
12.0.08
【分析】1公顷=10000平方米,根据高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率,据此解答即可。
【详解】800平方米=0.08公顷
【点睛】本题考查面积单位的转化和进率,高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率。
13.10.5
【分析】每个小方格的边长表示1cm,则1格的面积为1cm2。不规则图形的面积=整格数+半格数÷2(不满1格的按半格计算),据此解答。
【详解】整格数面积为6cm2,半格数的面积为9÷2=4.5cm2,所以阴影部分的面积为6+4.5=10.5cm2。
【点睛】本题主要考查不规则图形面积的估算,熟练掌握它的计算方法并灵活运用。
14./
【分析】将去年苹果的产量看作单位“1”,今年苹果的产量比去年多,今年的产量相当于去年的(1+),据此分析。
【详解】1+=
今年的产量相当于去年的。
15.
【分析】因为有49人参加期末考试,46人及格,则不及格的有3人;用不及格的人数除以总人数,结果用分数表示即可求出可能性的大小。
【详解】(49-46)÷49
=3÷49
=
抽中不及格的可能性为。
【点睛】本题主要考查可能性的大小,熟练掌握它的计算方法并灵活运用。
16.5;73
【分析】根据假分数换带分数的方法:用分子除以分母,得到的商是带分数的整数部分,分母不变,余数是分数的分子;带分数化假分数,用整数部分乘分母,加分子即可,分母不变,由此即可填空。
【详解】=
=
【点睛】本题主要考查带分数和假分数的互化,熟练掌握它们之间的关系是解题的关键。
17.300
【分析】观察图形可知,游泳馆的指示牌是由长是20cm,宽是10cm的长方形与底是20cm,高是10cm的三角形组成;根据长方形面积公式:面积=长×宽;三角形面积公式:面积=底×高÷2;代入数据,求出长方形面积和三角形面积,再相加,即可解答。
【详解】20×10+20×10÷2
=200+200÷2
=200+100
=300(cm2)
【点睛】利用长方形面积公式和三角形面积公式进行解答。
18. 40
【分析】把带分数转化成假分数,再根据分母判断分数单位是几分之一,根据分子判断有多少个这样的分数单位。
【详解】因为:==,所以:4的分数单位是,它有40个这样的分数单位。
【点睛】此题重点考查带分数化假分数的方法和对分数单位的认识。
19. 底 高 底×高÷2
【分析】观察可知,三角形的底与平行四边形的底相等,三角形的高等于平行四边形的高,又知平行四边形的面积是三角形的2倍,根据平行四边形的面积=底×高,可以推导出三角形的面积公式。
【详解】用两个同样的三角形拼成一个平行四边形(如图):经过观察,我们发现三角形的底等于平行四边形的底;三角形的高等于平行四边形的高;根据平行四边形的面积=底×高,可以推导出三角形的面积=底×高÷2。
20.(1)(2)见详解
【分析】(1)把数轴上一个单位长度看作单位“1”,把它平均分成4份,每份是,用真分数或假分数表示时,几份就是四分之几;用带分数表示时,几后面整数部分就是几,真分数按前面所述。
(2)2个是,把第一个单位长度平均分成3份,分数A表示其中的2份,据此即可在数轴上标出A;B是,根据(1)分析即可在数轴上标出B。
【详解】
【点睛】本题题是考查分数的意义。把单位“1”平均分成若干份,用分数表示,分母是平均分成的份数,分子是要表示的份数。
21.√
【分析】分别用1和这两个分数与1求差,差小的离1近。
【详解】
所以更接近1。原题说法正确。
故答案为:√
【点睛】本题主要考查分数大小的比较。
22.√
【分析】常用的面积单位有平方米、平方分米、平方厘米;其中测量土地的面积,可以用公顷作单位;计量比较大的土地面积常用公顷或平方千米作单位。
【详解】测量较大面积的土地时,一般用公顷或平方千米作单位;原题说法正确。
故答案为:√
【点睛】本题主要是考查常用的面积单位以及面积单位的选择。
23.×
【分析】三角形的面积=底×高÷2,将高是9分米,底是4分米的三角形的面积求出来,与题干作对比即可。
【详解】4×9÷2
=36÷2
=18(平方分米)
高是9分米,底是4分米的三角形的面积是18平方分米,与题干不符。
故答案为:×
24.√
【分析】如果a=b,且a=c,那么b=c,据此分析。
【详解】因为1÷3=,1÷3=0.333…,所以=0.333…,说法正确。
故答案为:√
25.×
【分析】当长方形被拉成平行四边形后,它的长和宽没变,所以周长不变,但是拉成的平行四边形的高小于长方形的宽,所以面积就变小了。据此判断。
【详解】把一个长方形活动框架拉成一个平行四边形,它的长和宽没变,所以周长不变,但是高变小了,所以面积就变小了。
因此,题干中的说法是错误的。
故答案为:×
【点睛】此题主要考查平行四边形易变形的特征,以及长方形和平行四边形的周长公式、面积公式的灵活应用。
26.×
【分析】确定一个图形面积的大小,不仅是根据图形的形状,更重要的是根据图形所占格子的多少来确定。
【详解】比如下面的正方形和长方形,都是占4个格子,它们的面积相等,形状却不同,所以原题说法错误;
故答案为:×
27.×
【分析】根据可能性知识,数量多的摸到的可能性就大,进而完成判断即可。
【详解】一个口袋里装有2个红球、5个黄球、1个白球,5>2>1,所以任意摸出1个球,摸到黄球的可能性最大。所以原题说法错误。
故答案为:×
【点睛】此题考查可能性的大小,数量多的摸到的可能性就大,根据日常生活经验判断。
28.=,=,>。
=,=,=。
=,=,<。
【分析】约分是根据分数的基本性质,一般用分子和分母的公因数(1除外)去除分数的分子和分母,通常要除到得出最简分数为止,再按照分数的大小比较的方法比较。
【详解】==,==
>
所以>
==,==
=
所以=
==,==
<
所以<
29.x=11;x=2.1;
【分析】第一个:根据等式的性质1,等式两边同时加上8,再根据等式的性质2,等式两边同时除以3即可;
第二个:根据等式的性质1,等式两边同时加上2.8x,再根据等式的性质2,等式两边同时除以6即可;
第三个:根据等式的性质1,等式两边同时加上8即可。
【详解】3x-8=25
解:3x=25+8
3x=33
x=33÷3
x=11
3.2x=12.6-2.8x
解:3.2x+2.8x=12.6
6x=12.6
x=12.6÷6
x=2.1
解:
30.(1)12
(2)(3)见详解
【分析】(1)看图可知,密室1的形状是个平行四边形,根据平行四边形的面积=底×高,列式计算即可;
(2)梯形的面积=(上底+下底)×高÷2,据此确定密室2的上底、下底和高,作图即可;
(3)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)4×3=12(平方米)
密室1的面积是12平方米。
(2)计算密室2的面积的算式是(平方米)可知,密室2的上底2米、下底4米、高4米(画法不唯一)。
(2)(3)作图如下:
31.(1)图见详解
(2)20
【分析】根据题意,第1组有2个●,第2组有2+3=5(个)●,第3组有5+3=8(个)●,后面的依次比前一组多3个●,据此解答即可。
【详解】(1)由分析可得:第1组有2个●
第2组:2+3=5(个)
第3组:5+3=8(个)
第4组:8+3=11(个)
作图如下:
(2)第5组:11+3=14(个)
第6组:14+3=17(个)
第7组:17+3=20(个)
按照这样的规律,第7组有20个●。
32.30厘米
【分析】根据平行四边形面积=底×高,求得平行四边形面积;再用平行四边形面积÷高,求得另一个底的长度,然后把两个底边相加乘2,即是需要铁丝的长度。
【详解】9×4÷6
=36÷6
=6(厘米)
(9+6)×2
=15×2
=30(厘米)
答:需要30的铁丝。
【点睛】灵活运用平行四边形面积公式是解答的关键。
33.(1)948平方米;0.0948公顷
(2)197棵
【分析】(1)观察图形可知,平行四边形的高等于长方形小路的长,这块平行四边形桃树地的占地面积,就是平行四边形面积减去小路的面积;根据平行四边形面积公式:面积=底×高;长方形面积公式:面积=长×宽,代入数据,求出桃树占地面积;1公顷=10000平方米,再化成公顷即可;
(2)用这块平行四边形桃树地的占地面积÷每颗桃树占地面积,即可求出这块平行四边形桃树地最多可以栽桃树的棵数。
【详解】42×24-24×2.5
=1008-60
=948(平方米)
948平方米=0.0948公顷
答:这块平行四边形桃树地的占地面积是948平方米,和0.0948公顷。
(2)948÷4.8≈197(棵)
答:这块平行四边形桃树地最多可以栽197棵桃树。
【点睛】熟练掌握平行四边形面积和长方形面积公式是解答本题的关键,注意单位名数的换算以及结果要用“去尾法”解答。
34.29.4吨
【分析】先根据梯形的面积=(上底+下底)×高÷2算出梯形果园的面积;再用果园的面积除以每棵树需要的种植面积可得到一共可以种植多少棵树;再用种植的棵树乘每棵果树可以收的苹果重量即可得到一共可以收多少千克苹果,最后根据1000千克=1吨,把单位换算成吨即可。
【详解】(180+240)×14÷2
=420×14÷2
=5880÷2
=2940(平方米)
2940÷15×150
=196×150
=29400(千克)
29400千克=29.4吨
答:这个果园最多可收苹果29.4吨。
【点睛】掌握梯形的面积公式及千克和吨之间的换算进率是解答本题的关键。
35.;
【分析】求男生捐款是全班捐款总数的几分之几,用男生捐款数除以全班捐款总数即可;
求女生捐款是全班捐款总数的几分之几,先用全班捐款总数减去男生捐款数,求出女生捐款数;再用女生捐款数除以全班捐款总数即可。
【详解】1100÷2000=
(2000-1100)÷2000
=900÷2000
=
答:男生捐款是全班捐款总数的,女生捐款是全班捐款总数的。
【点睛】本题考查分数与除法的关系,明确求一个数是另一个数的几分之几,用除法计算,计算结果能约分的要约成最简分数。
36.去时走得快
【分析】路程不变,只看去时用的时间少还是返回时用的时间少,用的时间少就快,据此比较h和h的大小即可。
【详解】=
=
<
所以<
答:宁宁去时走得快。
【点睛】明确走相同的路程,用的时间短的走得快是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
