《基础卷》——第五单元圆(单元测试)(含解析)-2025-2026学年六年级上册数学(北京版)
文档属性
| 名称 | 《基础卷》——第五单元圆(单元测试)(含解析)-2025-2026学年六年级上册数学(北京版) |

|
|
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 22:42:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《基础卷》——第五单元圆(单元测试)-2025-2026学年六年级上册数学(北京版)
一、单选题
1.《墨子·经上》记载:“圆,一中同长也”。对这句话的内涵解释错误的是( )
A.同一圆中,所有的半径都相等
B.同一圆中,所有的直径都相等
C.同一圆中,所有的线段都相等
2.下列说法中正确的是( )
A.圆周率就是3.14。
B.由于圆的位置不同,所以圆的周长不同。
C.直径是圆内最长的线段。
D.直径是线段,半径是射线。
3.一个小圆的半径是一个大圆半径的 ,那么这个小圆的周长是这个大圆周长的( )。
A. B.2倍 C. D.4倍
4.一个圆的直径由5分米减少到4分米,周长比原来减少原来的( ).
A. B. C. D.
5.一个圆的半径由6厘米增加到9厘米,则圆的面积增加( )平方厘米。
A.4π B.6π C.9π D.45π
6.下图中,从M到N走路线①和路线②的结果是( )。
A.路线①远 B.路线②远 C.同样远
7.甲圆半径是乙圆半径的 ,甲圆面积是120cm2,乙圆面积是( )。
A.180cm2 B.270cm2 C.80cm2
二、判断题
8.在同一个圆里,两条半径就是一条直径。( )
9.一个圆的周长是它直径的π倍,是它半径的2π倍。( )
10.一个半径是2cm的圆,面积和周长相等。( )
11.如图,笑笑认为阴影部分的周长与空白部分的周长的比是1:1。( )
12.用同样长的铁丝分别围成正方形和圆,其中圆的面积较大。( )
13.把一个圆的半径扩大到原来的3倍,这个圆的周长也会扩大到原来的3倍,而面积就会扩到了原来的9倍。( )
14.用12.56分米的铁丝分别围成长方形、正方形、圆,面积最大的是正方形。( )
15.在面积相等的长方形、正方形和圆中,周长最长的是长方形。( )
16.周长相等的正方形和圆中,圆的面积比较大。( )
三、填空题
17.在一个长 10 cm , 宽 4 cm 的长方形中画两个最大的圆(如下图),这两个圆的圆心相距 cm。
18.一个扇形的圆心角是90°,半径是2dm,这个扇形的面积是 dm 。
19.如果要画一个周长为12.56厘米的圆,那么圆规两脚间的距离应该取 厘米。圆的周长总是它的直径的 倍。
20.画圆时圆规两脚尖的距离是0.6cm,所画圆的周长是 ,面积是
21.一张CD盘的圆周长是37.68厘米,它的直径是 厘米,面积是 平方厘米.
22.用一根绳子围绕大树,如果绕10圈则剩下3米,如果绕12圈又缺3米,那么绕8圈剩下 米。
23.一种车子的车轮外直径70厘米,车子要通过长1099米的桥,车轮要转 圈
24.一个直径是10m的半圆形花坛的周长是 m,面积是 m2。
四、操作题
25.过A、B两点画一个最小的圆。
五、解决问题
26.公园里自动旋转喷灌装置半径是10m,它的最大喷灌面积是多少平方米
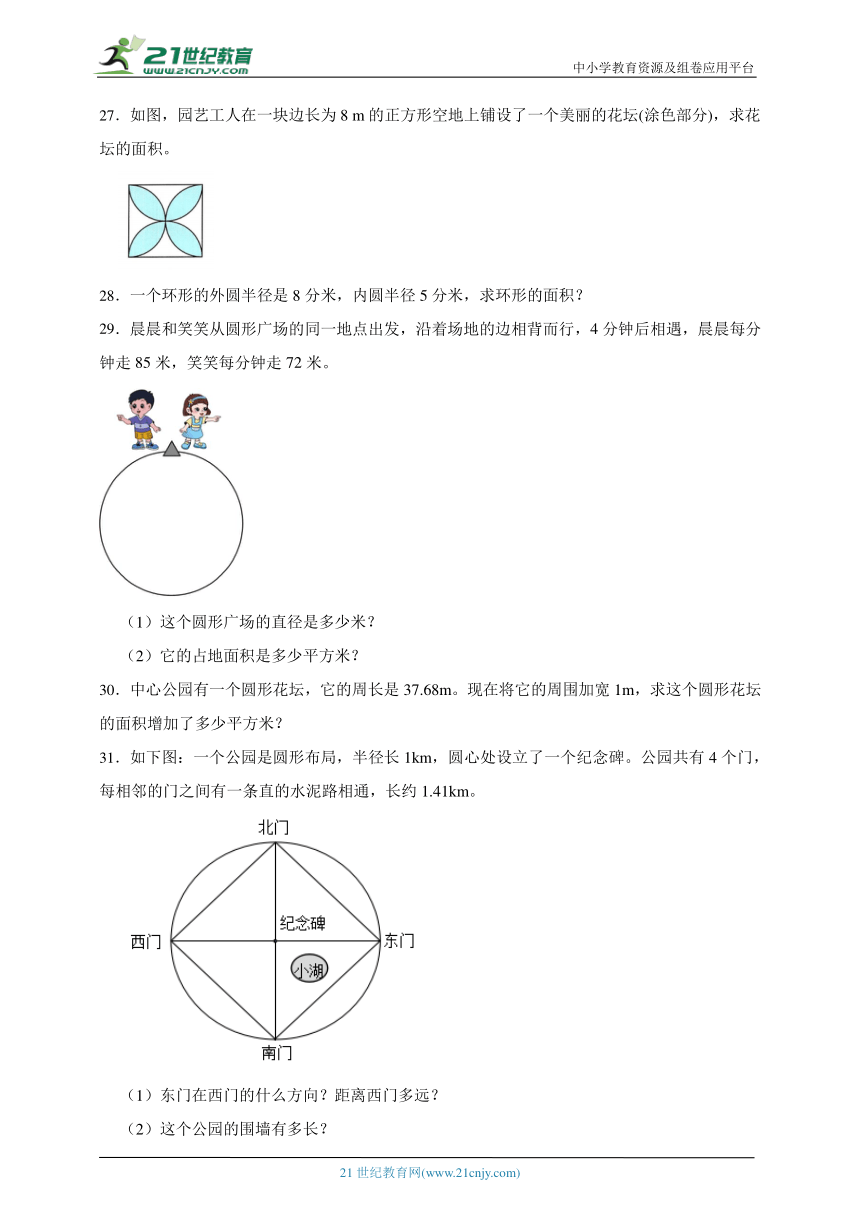
27.如图,园艺工人在一块边长为8 m的正方形空地上铺设了一个美丽的花坛(涂色部分),求花坛的面积。
28.一个环形的外圆半径是8分米,内圆半径5分米,求环形的面积?
29.晨晨和笑笑从圆形广场的同一地点出发,沿着场地的边相背而行,4分钟后相遇,晨晨每分钟走85米,笑笑每分钟走72米。
(1)这个圆形广场的直径是多少米?
(2)它的占地面积是多少平方米?
30.中心公园有一个圆形花坛,它的周长是37.68m。现在将它的周围加宽1m,求这个圆形花坛的面积增加了多少平方米?
31.如下图:一个公园是圆形布局,半径长1km,圆心处设立了一个纪念碑。公园共有4个门,每相邻的门之间有一条直的水泥路相通,长约1.41km。
(1)东门在西门的什么方向?距离西门多远?
(2)这个公园的围墙有多长?
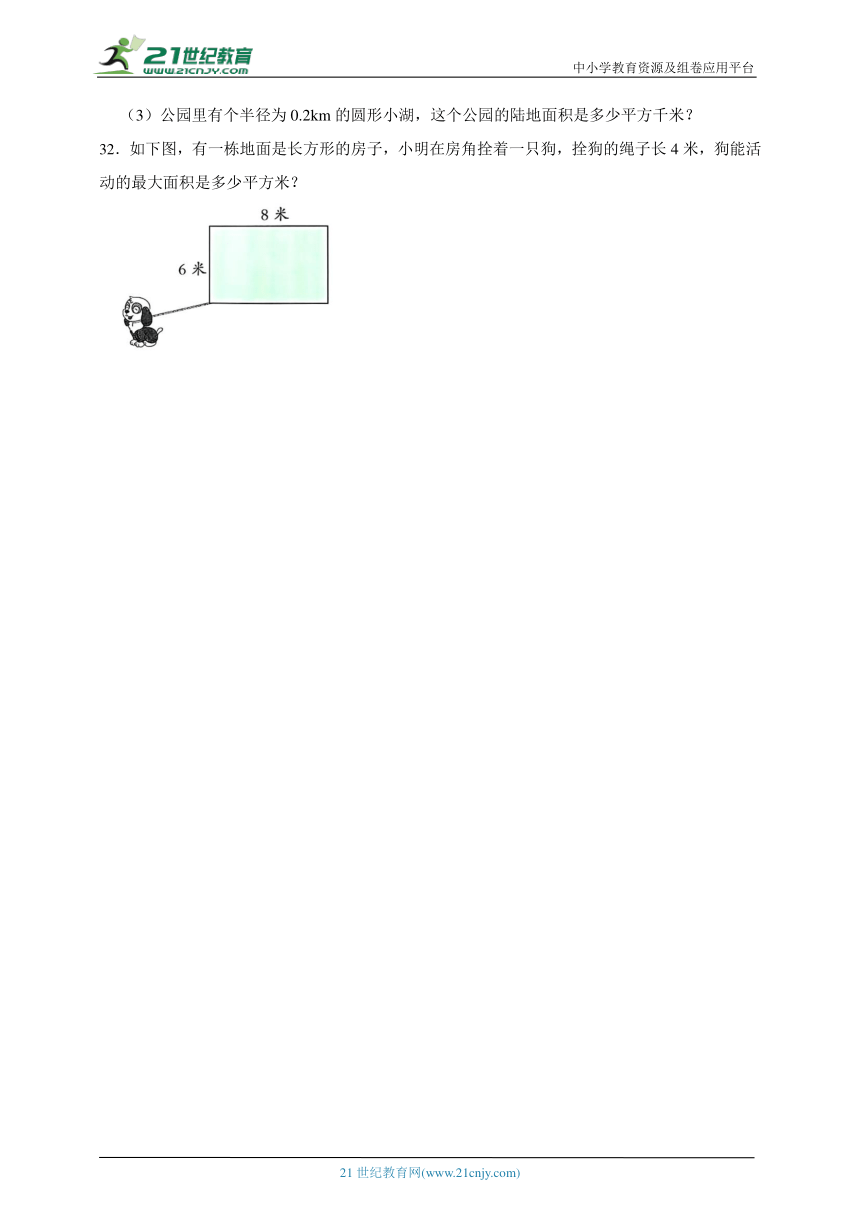
(3)公园里有个半径为0.2km的圆形小湖,这个公园的陆地面积是多少平方千米?
32.如下图,有一栋地面是长方形的房子,小明在房角拴着一只狗,拴狗的绳子长4米,狗能活动的最大面积是多少平方米?
答案解析部分
1.【答案】C
【解析】【解答】解:错误的应该是同一圆中,所有的线段都相等。
故答案为:C。
【分析】“圆,一中同长也”表示同一个圆中,所有的半径都相等,所有的直径也都相等。
2.【答案】C
【解析】【解答】解:A:圆周率的近似数是3.14,原来说法错误;
B:圆的周长与圆的位置无关,原来说法错误;
C:直径是圆内最长的线段,此说法正确;
D:直径和半径都是线段,原来说法错误。
故答案为:C。
【分析】A:圆周率是一个无限不循环小数,3.14是其近似数;
B:圆的周长与圆的直径或半径的大小有关,与圆的位置无关;
C:直径是通过圆心并且两端都在圆上的线段,直径是圆内最长的线段;
D:半径是连接圆心到圆上任意一点的线段,直径和半径都是线段。
3.【答案】A
【解析】【解答】解:假设大圆的半径是r,则小圆的半径是r。
(2×r×π)÷(2πr)=
故答案为:A。
【分析】这个小圆的周长是这个大圆周长的分率=小圆的周长÷大圆的周长;其中,圆的周长=2πr。
4.【答案】D
【解析】【解答】解:当圆的直径为5分米时,其周长为分米。
当圆的直径减少到4分米时,其周长为分米。
周长减少的部分为分米。
所以周长减少的比原来的比例为。
故答案为:D
【分析】题目要求找出一个圆的直径从5分米减少到4分米后,周长相比原来减少的比例。需要明确周长与直径的关系,即,其中是周长,是直径。通过这个公式,可以推导出直径改变时周长的变化比例。
5.【答案】D
【解析】【解答】92π-62π=81π-36π=45π(平方厘米)。
故答案为:D。
【分析】圆的面积公式:S=πr2,据此分别求出原来和现在圆的面积,然后用现在圆的面积-原来圆的面积=增加的面积,据此列式解答。
6.【答案】C
【解析】【解答】解:假设从左到右的小圆直径分别是a、b、c
路线①的长度:
π×(a+b+c)÷2=π(a+b+c);
路线②的长度:
π×a÷2+π×b÷2+π×c÷2
=πa+πb+πc
=π(a+b+c);
①=②
故答案为:C。
【分析】线路①的长度=π×直径÷2;线路②的长度=三个圆的周长÷2的和。
7.【答案】B
【解析】【解答】解:×=
120÷=270(cm2)
故答案为:B。
【分析】甲圆半径是乙圆半径的,所以甲圆面积是乙圆面积的,乙圆面积=甲圆面积÷。
8.【答案】错误
【解析】【解答】解:在同一个圆里,直径的是连接圆周上两点并通过圆心的直线。
故答案为:错误。
【分析】根据直径的概念作答即可。
9.【答案】正确
【解析】【解答】解:根据圆周长公式,C=πd=2πr推理。原题干说法正确。
故答案为:正确。
【分析】考查圆周长公式。
10.【答案】错误
11.【答案】正确
【解析】【解答】解:设正方形的边长是a
阴影部分的周长=π2a4+2a=(+2)a
空白部分的周长=π2a4+2a=(+2)a
故答案为:正确。
【分析】观察图形,阴影部分的周长和空白部分的周长均为圆的周长的,加上正方形边长的2倍,所以阴影部分的周长=空白部分的周长,也就是说阴影部分的周长与空白部分的周长的比是1:1。
12.【答案】正确
【解析】【解答】解:用同样长的铁丝分别围成正方形和圆,其中圆的面积较大,原题干说法正确。
故答案为:正确。
【分析】周长相等的长方形、正方形、圆中,圆的面积最大。
13.【答案】正确
【解析】【解答】解:把一个圆的半径扩大到原来的3倍,这个圆的周长也会扩大到原来的3倍,而面积就会扩到了原来的9倍。
故答案为:正确。
【分析】圆的周长=2πr,圆的面积=πr2,当圆的半径扩大到原来的3倍时,现在圆的周长=2π(r×3)=6πr=原来圆的周长×3;现在圆的面积=π(r×3)2=9πr2=原来圆的面积×9。
14.【答案】错误
【解析】【解答】解:①长方形的长可以为3.13分米,宽为3.15分米,面积是:
3.13×3.15=9.8595(平方分米);
②正方形的边长为3.14分米,面积是:
3.14×3.14=9.8596(平方分米);
③圆的面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方分米)
12.56平方分米>9.8596平方分米>9.8595平方分米
故答案为:错误。
【分析】 周长相等的长方形、正方形、圆,其中圆的面积最大,长方形的面积最小。
15.【答案】正确
【解析】【解答】解:设三种图形的面积均为4,则正方形的边长为2,周长为2×4=8;
圆的半径的平方为4÷3.14≈1,半径也约等于1,周长约为 2×3.14×1=6.28;此时正方形的周长比圆的周长长;
假设长方形的宽是1,长就是4,周长就是(1+4)×2=10,综合比较,长方形的周长最长。
故答案为:正确。
【分析】本题可以先假设出面积为4,然后分析对比正方形和圆的周长。对于长方形,可以假设出长和宽,也可以分析“当两个整数的积相等时,这两个数相等时其和最小,因此长方形与正方形面积相等,长方形的周长比正方形的周长长,所以面积相等的长方形、正方形和圆中,周长最长的是长方形”。
16.【答案】正确
【解析】【解答】解:假设正方形、圆,它们的周长为12.56厘米;
①正方形的边长为3.14厘米,面积是:
3.14×3.14=9.8596(平方厘米);
②圆的面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
12.56平方厘米>9.8596平方厘米
故答案为:正确。
【分析】周长相等的正方形和圆,其中圆的面积比较大。
17.【答案】4
【解析】【解答】解:4÷2=2(cm)
2+2=4(cm)
故答案为:4。
【分析】 在长方形中画最大的圆,长方形中较短的边就是圆的直径;图中两个圆的圆心的距离即是两个半径的和。
18.【答案】3.14
【解析】【解答】解:3.14×22÷4
=3.14×(4÷4)
=3.14(平方分米)。
故答案为:3.14。
【分析】这个扇形的面积=圆的面积÷4;其中,圆的面积=π×半径2。
19.【答案】2;π
【解析】【解答】解: 12.56÷3.14÷2=2(厘米)
圆的周长总是它的直径的π倍。
故答案为:2;π。
【分析】题目实际上是求圆的半径,依据圆的周长=2πr,代入数据即可求解; 根据圆的周长与直径之间的关系 完成填空。
20.【答案】3.768cm;1.1304平方厘米
【解析】【解答】解:3.14×2×0.6=3.768(厘米)
3.14×0.6×0.6=1.1304(平方厘米)
故答案为:3.768厘米;1.1304平方厘米。
【分析】圆的周长=2×π×圆的半径;圆的面积=π×半径的平方。
21.【答案】12;113.04
【解析】【解答】37.68÷3.14=12(厘米)
12÷2=6(厘米)
3.14×62
=3.14×36
=113.04(平方厘米)
故答案为:12;113.04
【分析】已知圆的周长,求圆的直径,用C÷π=d,然后用d÷2=r,求出圆的半径,最后用公式:S=πr2,据此列式解答.
22.【答案】9
【解析】【解答】 解:设树每圈绕x米,
12x-3=10x+3
12x-3-10x=10x+3-10x
2x-3=3
2x-3+3=3+3
2x=6
2x÷2=6÷2
x=3
绳子总长:
12×3-3
=36-3
=33(米)
绕8圈剩下:
33-8×3
=33-24
=9(米)
故答案为:9。
【分析】根据题意可知,无论绕几圈,这根绳子的总长是一定的,根据总长一定列方程解答,设树每圈绕x米,也就是树的横截面周长为x米,每圈的周长×12-3=每圈的周长×10+3,据此列方程可以求出绳子长度,然后用绳子的总长度-绕8圈的长度=剩下的长度,据此列式解答。
23.【答案】500
【解析】【解答】解:1099米=109900厘米
109900÷(3.14×70)
=109900÷219.8
=500(圈)
答:车轮要转500圈
【分析】车轮走过的路程,就是车轮周长的多少倍
24.【答案】25.7;39.25
【解析】【解答】解:3.14×10÷2+10
=31.4÷2+10
=15.7+10
=25.7(米)
10÷2=5(米)
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(平方米)。
故答案为:25.7;39.25。
【分析】半圆形花坛的周长=π×直径÷2+直径;半圆形花坛的面积=π×半径2÷2。
25.【答案】
【解析】【分析】根据题意,先连接AB两点,找出这条线段的中点,也就是圆心O的位置,然后以这个点为圆心,以AB长度的一半为半径画圆。
26.【答案】解:3.14×102=314(m2)
答:它的最大喷灌面积是314平方米。
【解析】【分析】圆面积公式:S=πr2。它最大的喷灌是一个圆形,半径是10米,根据圆面积公式计算即可。
27.【答案】解:8÷2=4(m)
8×8-42×3.14
=64-16×3.14
=64-50.24
=13.76(m2)
8×8-13.76×2
=64-27.52
=36.48(m2)
答:花坛的面积是36.48m2。
【解析】【分析】正方形的边长是8m,圆的直径也是8m,先用正方形的面积减去两个半圆(一个整圆)的面积,得到空白部分总面积的一半,进而得到空白部分的总面积,再用正方形的面积减去空白部分的总面积就是涂色部分的面积。
28.【答案】解:3.14×8 -3.14×5
=200.96-78.5
=122.46(平方分米)
答:环形的面积是122.46平方分米。
【解析】【分析】环形面积就是外圆面积减去内圆面积,根据圆面积公式计算即可,圆面积公式:S=πr 。
29.【答案】(1)解:(85+72)×4
=157×4
=628(米)
628÷3.14=200(米)
答:这个圆形广场的直径是200米。
(2)解:200÷2=100(米)
3.14×100×100=31400(平方米)
答:它的占地面积是31400平方米。
【解析】【分析】(1)根据速度和×相遇时间=总路程,求出广场周长,圆的直径=周长÷π,计算即可。
(2)根据圆的面积=πr2,列式解答即可。
30.【答案】解:37.68÷3.14÷2
=12÷2
=6(m)
6+1=7(m)
=3.14×(49-36)
=3.14×13
答:这个圆形花坛的面积增加了40.82平方米。
【解析】【分析】如图所示,求增加(绿色部分)的面积,实际上是求圆环的面积,用大圆的面积减小圆的面积即可;小圆的周长已知,利用圆的周长公式C=2πr即可求出小圆的半径,大圆的半径等于小圆的半径加上增加的宽度,从而利用圆环的面积公式S=π(R2-r2)即可求解。
31.【答案】(1)解:1×2=2(千米)
答:东门在西门的东方,距离西门2千米。
(2)解:3.14×2=6.28(千米)
答:这个公园的围墙有6.28千米。
(3)解:3.14×(12-0.22)
=3.14×0.96
=3.0144(平方千米)
答:这个公园的陆地面积是3.0144平方千米。
【解析】【分析】(1)东门到西门的距离=圆形公园的直径=半径×2;在地图上的方位是上北,下南,左西,右东;西南和东北相对,西北和东南相对;
(2)这个公园的围墙的长度=圆形公园的周长=π×直径;
(3)这个公园的陆地面积=π×(R2-r2)。
32.【答案】解:(360°-90°)÷360°=
(平方米)
答:狗能活动的最大面积是37.68平方米。
【解析】【分析】狗能活动的角度是一个圆的圆心角减去房子的一个90°的角,即270°,是一个圆的,所以狗能活动的最大面积是半径为4 米的圆的面积的 。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《基础卷》——第五单元圆(单元测试)-2025-2026学年六年级上册数学(北京版)
一、单选题
1.《墨子·经上》记载:“圆,一中同长也”。对这句话的内涵解释错误的是( )
A.同一圆中,所有的半径都相等
B.同一圆中,所有的直径都相等
C.同一圆中,所有的线段都相等
2.下列说法中正确的是( )
A.圆周率就是3.14。
B.由于圆的位置不同,所以圆的周长不同。
C.直径是圆内最长的线段。
D.直径是线段,半径是射线。
3.一个小圆的半径是一个大圆半径的 ,那么这个小圆的周长是这个大圆周长的( )。
A. B.2倍 C. D.4倍
4.一个圆的直径由5分米减少到4分米,周长比原来减少原来的( ).
A. B. C. D.
5.一个圆的半径由6厘米增加到9厘米,则圆的面积增加( )平方厘米。
A.4π B.6π C.9π D.45π
6.下图中,从M到N走路线①和路线②的结果是( )。
A.路线①远 B.路线②远 C.同样远
7.甲圆半径是乙圆半径的 ,甲圆面积是120cm2,乙圆面积是( )。
A.180cm2 B.270cm2 C.80cm2
二、判断题
8.在同一个圆里,两条半径就是一条直径。( )
9.一个圆的周长是它直径的π倍,是它半径的2π倍。( )
10.一个半径是2cm的圆,面积和周长相等。( )
11.如图,笑笑认为阴影部分的周长与空白部分的周长的比是1:1。( )
12.用同样长的铁丝分别围成正方形和圆,其中圆的面积较大。( )
13.把一个圆的半径扩大到原来的3倍,这个圆的周长也会扩大到原来的3倍,而面积就会扩到了原来的9倍。( )
14.用12.56分米的铁丝分别围成长方形、正方形、圆,面积最大的是正方形。( )
15.在面积相等的长方形、正方形和圆中,周长最长的是长方形。( )
16.周长相等的正方形和圆中,圆的面积比较大。( )
三、填空题
17.在一个长 10 cm , 宽 4 cm 的长方形中画两个最大的圆(如下图),这两个圆的圆心相距 cm。
18.一个扇形的圆心角是90°,半径是2dm,这个扇形的面积是 dm 。
19.如果要画一个周长为12.56厘米的圆,那么圆规两脚间的距离应该取 厘米。圆的周长总是它的直径的 倍。
20.画圆时圆规两脚尖的距离是0.6cm,所画圆的周长是 ,面积是
21.一张CD盘的圆周长是37.68厘米,它的直径是 厘米,面积是 平方厘米.
22.用一根绳子围绕大树,如果绕10圈则剩下3米,如果绕12圈又缺3米,那么绕8圈剩下 米。
23.一种车子的车轮外直径70厘米,车子要通过长1099米的桥,车轮要转 圈
24.一个直径是10m的半圆形花坛的周长是 m,面积是 m2。
四、操作题
25.过A、B两点画一个最小的圆。
五、解决问题
26.公园里自动旋转喷灌装置半径是10m,它的最大喷灌面积是多少平方米
27.如图,园艺工人在一块边长为8 m的正方形空地上铺设了一个美丽的花坛(涂色部分),求花坛的面积。
28.一个环形的外圆半径是8分米,内圆半径5分米,求环形的面积?
29.晨晨和笑笑从圆形广场的同一地点出发,沿着场地的边相背而行,4分钟后相遇,晨晨每分钟走85米,笑笑每分钟走72米。
(1)这个圆形广场的直径是多少米?
(2)它的占地面积是多少平方米?
30.中心公园有一个圆形花坛,它的周长是37.68m。现在将它的周围加宽1m,求这个圆形花坛的面积增加了多少平方米?
31.如下图:一个公园是圆形布局,半径长1km,圆心处设立了一个纪念碑。公园共有4个门,每相邻的门之间有一条直的水泥路相通,长约1.41km。
(1)东门在西门的什么方向?距离西门多远?
(2)这个公园的围墙有多长?
(3)公园里有个半径为0.2km的圆形小湖,这个公园的陆地面积是多少平方千米?
32.如下图,有一栋地面是长方形的房子,小明在房角拴着一只狗,拴狗的绳子长4米,狗能活动的最大面积是多少平方米?
答案解析部分
1.【答案】C
【解析】【解答】解:错误的应该是同一圆中,所有的线段都相等。
故答案为:C。
【分析】“圆,一中同长也”表示同一个圆中,所有的半径都相等,所有的直径也都相等。
2.【答案】C
【解析】【解答】解:A:圆周率的近似数是3.14,原来说法错误;
B:圆的周长与圆的位置无关,原来说法错误;
C:直径是圆内最长的线段,此说法正确;
D:直径和半径都是线段,原来说法错误。
故答案为:C。
【分析】A:圆周率是一个无限不循环小数,3.14是其近似数;
B:圆的周长与圆的直径或半径的大小有关,与圆的位置无关;
C:直径是通过圆心并且两端都在圆上的线段,直径是圆内最长的线段;
D:半径是连接圆心到圆上任意一点的线段,直径和半径都是线段。
3.【答案】A
【解析】【解答】解:假设大圆的半径是r,则小圆的半径是r。
(2×r×π)÷(2πr)=
故答案为:A。
【分析】这个小圆的周长是这个大圆周长的分率=小圆的周长÷大圆的周长;其中,圆的周长=2πr。
4.【答案】D
【解析】【解答】解:当圆的直径为5分米时,其周长为分米。
当圆的直径减少到4分米时,其周长为分米。
周长减少的部分为分米。
所以周长减少的比原来的比例为。
故答案为:D
【分析】题目要求找出一个圆的直径从5分米减少到4分米后,周长相比原来减少的比例。需要明确周长与直径的关系,即,其中是周长,是直径。通过这个公式,可以推导出直径改变时周长的变化比例。
5.【答案】D
【解析】【解答】92π-62π=81π-36π=45π(平方厘米)。
故答案为:D。
【分析】圆的面积公式:S=πr2,据此分别求出原来和现在圆的面积,然后用现在圆的面积-原来圆的面积=增加的面积,据此列式解答。
6.【答案】C
【解析】【解答】解:假设从左到右的小圆直径分别是a、b、c
路线①的长度:
π×(a+b+c)÷2=π(a+b+c);
路线②的长度:
π×a÷2+π×b÷2+π×c÷2
=πa+πb+πc
=π(a+b+c);
①=②
故答案为:C。
【分析】线路①的长度=π×直径÷2;线路②的长度=三个圆的周长÷2的和。
7.【答案】B
【解析】【解答】解:×=
120÷=270(cm2)
故答案为:B。
【分析】甲圆半径是乙圆半径的,所以甲圆面积是乙圆面积的,乙圆面积=甲圆面积÷。
8.【答案】错误
【解析】【解答】解:在同一个圆里,直径的是连接圆周上两点并通过圆心的直线。
故答案为:错误。
【分析】根据直径的概念作答即可。
9.【答案】正确
【解析】【解答】解:根据圆周长公式,C=πd=2πr推理。原题干说法正确。
故答案为:正确。
【分析】考查圆周长公式。
10.【答案】错误
11.【答案】正确
【解析】【解答】解:设正方形的边长是a
阴影部分的周长=π2a4+2a=(+2)a
空白部分的周长=π2a4+2a=(+2)a
故答案为:正确。
【分析】观察图形,阴影部分的周长和空白部分的周长均为圆的周长的,加上正方形边长的2倍,所以阴影部分的周长=空白部分的周长,也就是说阴影部分的周长与空白部分的周长的比是1:1。
12.【答案】正确
【解析】【解答】解:用同样长的铁丝分别围成正方形和圆,其中圆的面积较大,原题干说法正确。
故答案为:正确。
【分析】周长相等的长方形、正方形、圆中,圆的面积最大。
13.【答案】正确
【解析】【解答】解:把一个圆的半径扩大到原来的3倍,这个圆的周长也会扩大到原来的3倍,而面积就会扩到了原来的9倍。
故答案为:正确。
【分析】圆的周长=2πr,圆的面积=πr2,当圆的半径扩大到原来的3倍时,现在圆的周长=2π(r×3)=6πr=原来圆的周长×3;现在圆的面积=π(r×3)2=9πr2=原来圆的面积×9。
14.【答案】错误
【解析】【解答】解:①长方形的长可以为3.13分米,宽为3.15分米,面积是:
3.13×3.15=9.8595(平方分米);
②正方形的边长为3.14分米,面积是:
3.14×3.14=9.8596(平方分米);
③圆的面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方分米)
12.56平方分米>9.8596平方分米>9.8595平方分米
故答案为:错误。
【分析】 周长相等的长方形、正方形、圆,其中圆的面积最大,长方形的面积最小。
15.【答案】正确
【解析】【解答】解:设三种图形的面积均为4,则正方形的边长为2,周长为2×4=8;
圆的半径的平方为4÷3.14≈1,半径也约等于1,周长约为 2×3.14×1=6.28;此时正方形的周长比圆的周长长;
假设长方形的宽是1,长就是4,周长就是(1+4)×2=10,综合比较,长方形的周长最长。
故答案为:正确。
【分析】本题可以先假设出面积为4,然后分析对比正方形和圆的周长。对于长方形,可以假设出长和宽,也可以分析“当两个整数的积相等时,这两个数相等时其和最小,因此长方形与正方形面积相等,长方形的周长比正方形的周长长,所以面积相等的长方形、正方形和圆中,周长最长的是长方形”。
16.【答案】正确
【解析】【解答】解:假设正方形、圆,它们的周长为12.56厘米;
①正方形的边长为3.14厘米,面积是:
3.14×3.14=9.8596(平方厘米);
②圆的面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
12.56平方厘米>9.8596平方厘米
故答案为:正确。
【分析】周长相等的正方形和圆,其中圆的面积比较大。
17.【答案】4
【解析】【解答】解:4÷2=2(cm)
2+2=4(cm)
故答案为:4。
【分析】 在长方形中画最大的圆,长方形中较短的边就是圆的直径;图中两个圆的圆心的距离即是两个半径的和。
18.【答案】3.14
【解析】【解答】解:3.14×22÷4
=3.14×(4÷4)
=3.14(平方分米)。
故答案为:3.14。
【分析】这个扇形的面积=圆的面积÷4;其中,圆的面积=π×半径2。
19.【答案】2;π
【解析】【解答】解: 12.56÷3.14÷2=2(厘米)
圆的周长总是它的直径的π倍。
故答案为:2;π。
【分析】题目实际上是求圆的半径,依据圆的周长=2πr,代入数据即可求解; 根据圆的周长与直径之间的关系 完成填空。
20.【答案】3.768cm;1.1304平方厘米
【解析】【解答】解:3.14×2×0.6=3.768(厘米)
3.14×0.6×0.6=1.1304(平方厘米)
故答案为:3.768厘米;1.1304平方厘米。
【分析】圆的周长=2×π×圆的半径;圆的面积=π×半径的平方。
21.【答案】12;113.04
【解析】【解答】37.68÷3.14=12(厘米)
12÷2=6(厘米)
3.14×62
=3.14×36
=113.04(平方厘米)
故答案为:12;113.04
【分析】已知圆的周长,求圆的直径,用C÷π=d,然后用d÷2=r,求出圆的半径,最后用公式:S=πr2,据此列式解答.
22.【答案】9
【解析】【解答】 解:设树每圈绕x米,
12x-3=10x+3
12x-3-10x=10x+3-10x
2x-3=3
2x-3+3=3+3
2x=6
2x÷2=6÷2
x=3
绳子总长:
12×3-3
=36-3
=33(米)
绕8圈剩下:
33-8×3
=33-24
=9(米)
故答案为:9。
【分析】根据题意可知,无论绕几圈,这根绳子的总长是一定的,根据总长一定列方程解答,设树每圈绕x米,也就是树的横截面周长为x米,每圈的周长×12-3=每圈的周长×10+3,据此列方程可以求出绳子长度,然后用绳子的总长度-绕8圈的长度=剩下的长度,据此列式解答。
23.【答案】500
【解析】【解答】解:1099米=109900厘米
109900÷(3.14×70)
=109900÷219.8
=500(圈)
答:车轮要转500圈
【分析】车轮走过的路程,就是车轮周长的多少倍
24.【答案】25.7;39.25
【解析】【解答】解:3.14×10÷2+10
=31.4÷2+10
=15.7+10
=25.7(米)
10÷2=5(米)
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(平方米)。
故答案为:25.7;39.25。
【分析】半圆形花坛的周长=π×直径÷2+直径;半圆形花坛的面积=π×半径2÷2。
25.【答案】
【解析】【分析】根据题意,先连接AB两点,找出这条线段的中点,也就是圆心O的位置,然后以这个点为圆心,以AB长度的一半为半径画圆。
26.【答案】解:3.14×102=314(m2)
答:它的最大喷灌面积是314平方米。
【解析】【分析】圆面积公式:S=πr2。它最大的喷灌是一个圆形,半径是10米,根据圆面积公式计算即可。
27.【答案】解:8÷2=4(m)
8×8-42×3.14
=64-16×3.14
=64-50.24
=13.76(m2)
8×8-13.76×2
=64-27.52
=36.48(m2)
答:花坛的面积是36.48m2。
【解析】【分析】正方形的边长是8m,圆的直径也是8m,先用正方形的面积减去两个半圆(一个整圆)的面积,得到空白部分总面积的一半,进而得到空白部分的总面积,再用正方形的面积减去空白部分的总面积就是涂色部分的面积。
28.【答案】解:3.14×8 -3.14×5
=200.96-78.5
=122.46(平方分米)
答:环形的面积是122.46平方分米。
【解析】【分析】环形面积就是外圆面积减去内圆面积,根据圆面积公式计算即可,圆面积公式:S=πr 。
29.【答案】(1)解:(85+72)×4
=157×4
=628(米)
628÷3.14=200(米)
答:这个圆形广场的直径是200米。
(2)解:200÷2=100(米)
3.14×100×100=31400(平方米)
答:它的占地面积是31400平方米。
【解析】【分析】(1)根据速度和×相遇时间=总路程,求出广场周长,圆的直径=周长÷π,计算即可。
(2)根据圆的面积=πr2,列式解答即可。
30.【答案】解:37.68÷3.14÷2
=12÷2
=6(m)
6+1=7(m)
=3.14×(49-36)
=3.14×13
答:这个圆形花坛的面积增加了40.82平方米。
【解析】【分析】如图所示,求增加(绿色部分)的面积,实际上是求圆环的面积,用大圆的面积减小圆的面积即可;小圆的周长已知,利用圆的周长公式C=2πr即可求出小圆的半径,大圆的半径等于小圆的半径加上增加的宽度,从而利用圆环的面积公式S=π(R2-r2)即可求解。
31.【答案】(1)解:1×2=2(千米)
答:东门在西门的东方,距离西门2千米。
(2)解:3.14×2=6.28(千米)
答:这个公园的围墙有6.28千米。
(3)解:3.14×(12-0.22)
=3.14×0.96
=3.0144(平方千米)
答:这个公园的陆地面积是3.0144平方千米。
【解析】【分析】(1)东门到西门的距离=圆形公园的直径=半径×2;在地图上的方位是上北,下南,左西,右东;西南和东北相对,西北和东南相对;
(2)这个公园的围墙的长度=圆形公园的周长=π×直径;
(3)这个公园的陆地面积=π×(R2-r2)。
32.【答案】解:(360°-90°)÷360°=
(平方米)
答:狗能活动的最大面积是37.68平方米。
【解析】【分析】狗能活动的角度是一个圆的圆心角减去房子的一个90°的角,即270°,是一个圆的,所以狗能活动的最大面积是半径为4 米的圆的面积的 。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
