第4章 图形的认识(新课预习.培优卷)(含解析)-2025-2026学年七年级上册数学湘教版(2024)
文档属性
| 名称 | 第4章 图形的认识(新课预习.培优卷)(含解析)-2025-2026学年七年级上册数学湘教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 933.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 12:33:26 | ||
图片预览



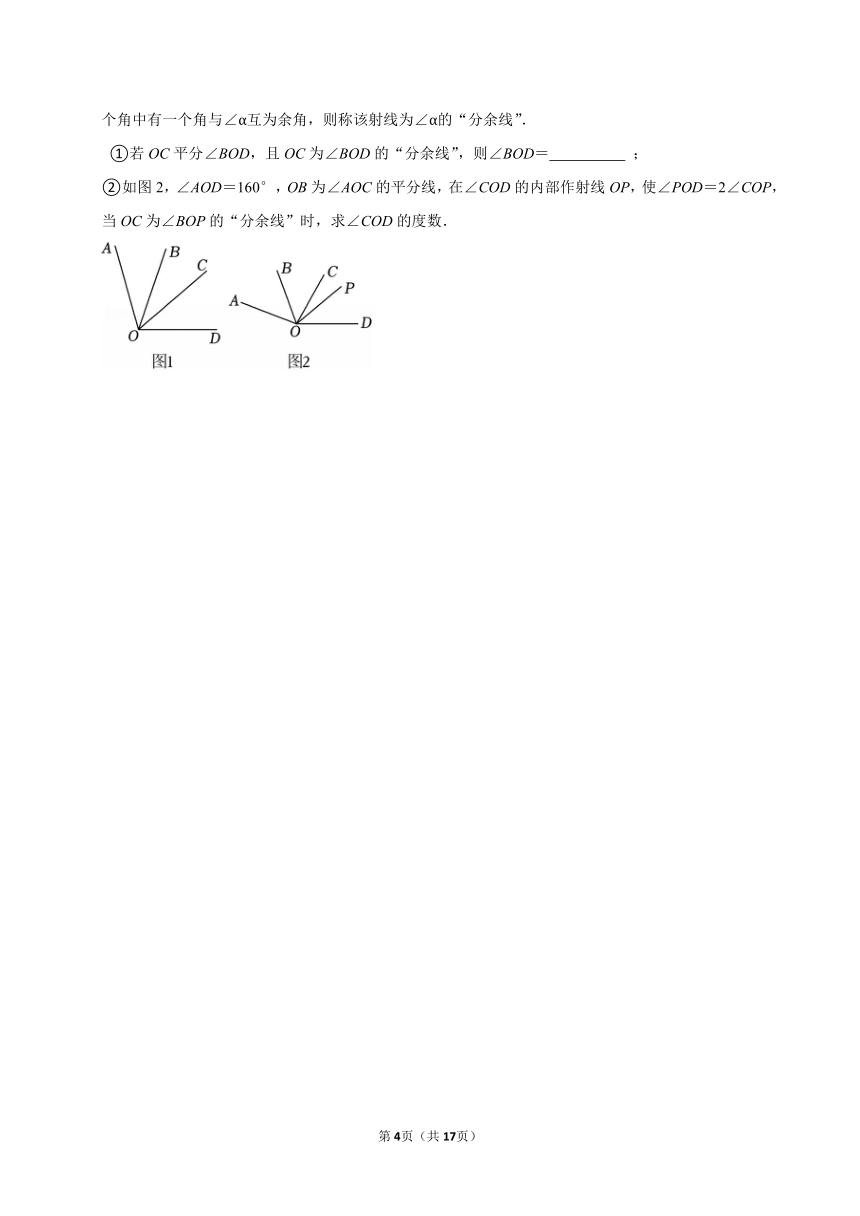

文档简介
第4章 图形的认识
一、选择题
1.下列图形中是圆柱的是( )
A. B.
C. D.
2.如图,利用量角器可知∠AOB的度数为( )
A.150° B.30° C.40° D.60°
3.已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
4.如图,A,B位于数轴上原点两侧,且OB=2OA.若点B表示的数是6,则点A表示的数是( )
A.﹣2 B.﹣3 C.﹣4 D.﹣5
5.“争创全国文明卫生城市,让文明成为我县人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( )
A.文 B.明 C.卫 D.生
6.互不重合的A、B、C三点在同一直线上,已知AB=2a,AC=a+6,BC=3a+1,则这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
二、填空题
7.如图,将一副三角板的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= °.
8.如图,点O在直线AB上,OD是∠BOC的平分线,若∠AOC=140°,则∠AOD的度数为 .
三、解答题
9.根据以下素材,探索完成任务.
时钟里的数学问题
素材1 时钟是我们日常生活中常用的生活用品,钟表上的时针和分针都绕其轴心旋转,如图1,表盘中1~12均匀分布,分针60分钟转动一周是360°时针60分钟移动一周的是30°,这样,分针转速为每分钟转6度,时针转速为每分钟转0.5度.
素材2 当时钟显示10:10时(如图2),时针与分针所成角度多少度?解决这个问题,可以先考虑10:00时,时针与分针所成角度为60°;从10:00到10:10,分针转动的角度为10×6=60°时针转动的角度为10×0.5=5°,60+60﹣5=115°因此10点10分时,时针与分针所成角度是115°.
素材3 当时针和分针所成角度180°时,我们将这样的时刻称为“美妙时刻”.如图3,当时钟显示6:00时,此时,时针和分针所成角度180°因此6:00就是一个美妙时刻.
解决问题
任务1 当时钟显示11:10分时,求时针与分针所成角度.
任务2 时钟显示1:00时,时针与分针所成角度为30°在1:00到1:30的30分钟内,小明发现存在着时针和分针垂直的情况,请求出此时的时刻.
任务3 6:00之后的下一个美妙时刻是 .一天24个小时内,共有 个美妙时刻.
10.如图,A,B,C,D四点在同一直线上.
(1)若AB=CD,比较线段的大小:AC BD(填“>”“<”或“=”).
(2)在(1)的基础上,若,且AC=16,求AD的长.
(3)若AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,求BC的长.
(4)若线段AD被点B,C分成了长度比为2:3:4的三部分,且AB的中点M和CD的中点N之间的距离是18,求AD的长.
(5)若AD=24,动点P从A出发,以每秒2个单位的速度沿射线AD方向运动,运动时间为t(t>0)秒,点Q为AP的中点.
①当t为何值时,点P恰好是QD的中点?
②当t为何值时,AQ=2PD?
11.如图1,已知射线OA,OB,OC,OD.
(1)若,且∠AOC=80°,求∠AOD的度数.
(2)若∠AOD=120°,OB是∠AOC的平分线,OC是∠AOD的平分线,求∠BOD的度数.
(3)若∠AOB:∠BOC:∠COD=2:3:4,OM,ON分别是∠AOB和∠COD的平分线,∠MON=90°,求∠AOD的度数.
(4)定义:从∠α(45°<α<90°)的顶点出发,在角的内部作一条射线,若该射线将∠α分得的两个角中有一个角与∠α互为余角,则称该射线为∠α的“分余线”.
①若OC平分∠BOD,且OC为∠BOD的“分余线”,则∠BOD= ;
②如图2,∠AOD=160°,OB为∠AOC的平分线,在∠COD的内部作射线OP,使∠POD=2∠COP,当OC为∠BOP的“分余线”时,求∠COD的度数.
第4章 图形的认识
参考答案与试题解析
一、选择题
1.下列图形中是圆柱的是( )
A. B.
C. D.
【答案】B
【分析】根据圆柱体的概念和定义,圆柱体的上下两个底面是圆形,平行且相等.
【解答】解:根据以上分析B为圆柱体.
故选:B.
【点评】本题考查的是圆柱的定义,关键点在于:圆柱体上下底面是圆形且平行和相等的.
2.如图,利用量角器可知∠AOB的度数为( )
A.150° B.30° C.40° D.60°
【答案】B
【分析】利用对顶角相等即可求得.
【解答】解:因为对顶角相等,
所以∠AOB的度数为30°,
故选:B.
【点评】本题考查的是对顶角的度数,解题的关键是会识图,了解对顶角相等.
3.已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
【答案】B
【分析】根据余角的定义,两个锐角和为90°的角互余.
【解答】解:由题意得:∠α=25°30′,
故其余角为(90°﹣∠α)=64°30′.
故选:B.
【点评】本题考查的知识点是两个角的互余,互余的两个角的和为90°.
4.如图,A,B位于数轴上原点两侧,且OB=2OA.若点B表示的数是6,则点A表示的数是( )
A.﹣2 B.﹣3 C.﹣4 D.﹣5
【答案】B
【分析】根据条件求出OA的长度,点A在原点的左侧,点A为负数,从而得出答案.
【解答】解:∵点B表示的数是6,
∴OB=6,
∵OB=2OA,
∴OA=3,
∴点A表示的数为﹣3,
故选:B.
【点评】本题考查了实数与数轴,根据条件求出OA的长度是解题的关键.
5.“争创全国文明卫生城市,让文明成为我县人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( )
A.文 B.明 C.卫 D.生
【答案】B
【分析】根据正方体的表面展开图找相对面的方法:“Z”字两端是对面,即可解答.
【解答】解:把展开图折叠成正方体后,“城”字对面的字是明,
故选:B.
【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.
6.互不重合的A、B、C三点在同一直线上,已知AB=2a,AC=a+6,BC=3a+1,则这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
【答案】B
【分析】用假设法分别计算各选项中的a值,再根据a>0判断即可.
【解答】解:∵AC=a+6,BC=3a+1,AB=2a,A、B、C三点互不重合,
∴a>0,
若点A在B、C之间,
则AB+AC=BC,
即2a+a+6=3a+1,
此时无解,
故此情况不存在,
若点B在A、C之间,
则BC+AB=AC,
3a+1+2a=a+6,
a,
故此情况存在,
若点C在A、B之间,
则BC+AC=AB,
即3a+1+a+6=2a,
a,
故此情况不存在,
∵互不重合的A、B、C三点在同一直线上,
故选:B.
【点评】本题主要考查两点间的距离及整式的加减,分类讨论和反证法的应用是解题的关键.
二、填空题
7.如图,将一副三角板的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= 30 °.
【答案】见试题解答内容
【分析】从图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解.
【解答】解:∵∠AOB=∠COD=90°,∠AOD=150°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.
故答案为:30.
【点评】此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.
8.如图,点O在直线AB上,OD是∠BOC的平分线,若∠AOC=140°,则∠AOD的度数为 160° .
【答案】见试题解答内容
【分析】根据邻补角定义求得∠BOC的度数,再根据角平分线定义即可求得答案.
【解答】解:∵∠AOC=140°,
∴∠BOC=180°﹣140°=40°,
∵OD是∠BOC的平分线,
∴∠BOD∠BOC=20°,
∴∠AOD=180°﹣20°=160°,
故答案为:160°.
【点评】本题主要考查角平分线的定义,此为几何中基础且重要知识点,必须熟练掌握.
三、解答题
9.根据以下素材,探索完成任务.
时钟里的数学问题
素材1 时钟是我们日常生活中常用的生活用品,钟表上的时针和分针都绕其轴心旋转,如图1,表盘中1~12均匀分布,分针60分钟转动一周是360°时针60分钟移动一周的是30°,这样,分针转速为每分钟转6度,时针转速为每分钟转0.5度.
素材2 当时钟显示10:10时(如图2),时针与分针所成角度多少度?解决这个问题,可以先考虑10:00时,时针与分针所成角度为60°;从10:00到10:10,分针转动的角度为10×6=60°时针转动的角度为10×0.5=5°,60+60﹣5=115°因此10点10分时,时针与分针所成角度是115°.
素材3 当时针和分针所成角度180°时,我们将这样的时刻称为“美妙时刻”.如图3,当时钟显示6:00时,此时,时针和分针所成角度180°因此6:00就是一个美妙时刻.
解决问题
任务1 当时钟显示11:10分时,求时针与分针所成角度.
任务2 时钟显示1:00时,时针与分针所成角度为30°在1:00到1:30的30分钟内,小明发现存在着时针和分针垂直的情况,请求出此时的时刻.
任务3 6:00之后的下一个美妙时刻是 7: .一天24个小时内,共有 22 个美妙时刻.
【答案】任务一:85°;
任务二:1:;
任务三:7:,22.
【分析】任务一:利用时针与分针所成角度=30°+分针转过的度数﹣时针转过的度数,即可求出结论;
任务二:设1点x分时,时针与分针垂直,利用分针转过的度数﹣(时针转过的度数+30°)=90°,可列出关于x的一元一次方程,解之即可得出结论;
任务三:设再经过y分钟,时针和分针所成角度第一次为180°,利用分针转过的度数﹣时针转过的度数=360°,可列出关于y的一元一次方程,解之可得出6:00之后的下一个美妙时刻是7:;设从0:00开始经过m分钟,时针和分针所成角度为180°,利用分针转过的度数﹣时针转过的度数=180°的奇数倍,可列出关于m的一元一次方程,解之可得出m,结合m≤60×24,可列出关于n的一元一次不等式,解之可得出n的取值范围,再结合n为正整数,即可得出结论.
【解答】解:任务一:30°+10×6°﹣10×0.5°=85°.
答:当时钟显示11:10时,时针与分针所成角度为85°;
任务二:设1点x分时,时针与分针垂直,
根据题意得:6x﹣(30+0.5x)=90,
解得:x.
答:此时的时刻为1:;
任务三:设再经过y分钟,时针和分针所成角度第一次为180°,
根据题意得:6y﹣0.5y=360,
解得:y60,
∴6:00之后的下一个美妙时刻是7:;
从0:00开始经过m分钟,时针和分针所成角度为180°,
根据题意得:6m﹣0.5m=180(2n﹣1)(n为正整数),
解得:m,
∵m≤60×24,
∴60×24,
解得:n,
又∵n为正整数,
∴n的最大值为22,
∴一天24个小时内,共有22个美妙时刻.
故答案为:7:,22.
【点评】本题考查了一元一次方程的应用、钟面角、分数的除法以及解一元一次不等式,找准等量关系,正确列出一元一次方程是解题的关键.
10.如图,A,B,C,D四点在同一直线上.
(1)若AB=CD,比较线段的大小:AC = BD(填“>”“<”或“=”).
(2)在(1)的基础上,若,且AC=16,求AD的长.
(3)若AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,求BC的长.
(4)若线段AD被点B,C分成了长度比为2:3:4的三部分,且AB的中点M和CD的中点N之间的距离是18,求AD的长.
(5)若AD=24,动点P从A出发,以每秒2个单位的速度沿射线AD方向运动,运动时间为t(t>0)秒,点Q为AP的中点.
①当t为何值时,点P恰好是QD的中点?
②当t为何值时,AQ=2PD?
【答案】(1)=;
(2)20;
(3)2;
(4)27;
(5)①8秒;
②秒或16秒.
【分析】(1)根据题意,AB=CD,则AB+BC=CD+BC,由线段的大小比较进而得出答案;
(2)根据题意,,AC=16,可得出BC的长,进而得出AB的长,由(1)可知AB=CD,进而得出AD的长;
(3)由题意可知,AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,可求出AB,AC的长,根据BC=AC﹣AB,即可得出答案;
(4)由题意可知,M是线段AB的中点,AB:BC:CD=2:3:4,得出AM=BM,设AM=BM=x,从而得出AB=2x,BC=3x,CD=4x,进而得出AD=9x,再根据已知N是线段CD的中点,MN=18,得出CN=DN=2x,列出方程:x+3x+2x=18,解一元一次方程求出x的值,进而得出答案;
(5)①根据题意可得AP=2t,,再根据已知点P是QD的中点,所以得出QP=PD=t,进而得出AD=3AQ=3t=24,求出t值即可;
②分两种情况:点P在点D的左侧和右侧,根据如图可得,PD=AD﹣AP=24﹣2t,或PD=AP﹣AD=2t﹣24,再根据AQ=2PD,列出关于t的方程,进而得出t的值.
【解答】解:(1)∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD.
故答案为:=;
(2)∵,AC=16,
∴,
∴AB=AC﹣BC=16﹣12=4,
在(1)的基础上,∵AB=CD,
∴CD=4,
∴AD=AC+CD=16+4=20.
(3)如图所示:
由题意可知,AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,
∴,,
∴BC=AC﹣AB=6﹣4=2;
(4)如图所示:
∵M是线段AB的中点,AB:BC:CD=2:3:4,
∴AM=BM,
设AM=BM=x,
∴AB=2x,BC=3x,CD=4x,
∴AD=AB+BC+CD=2x+3x+4x=9x.
∵N是线段CD的中点,MN=18,
∴CN=DN=2x,
∴x+3x+2x=18,
解得:x=3,
∴AD=9x=9×3=27.
(5)①如图所示:
∵点Q是AP的中点,AP=2t,
∴,
又∵点P是QD的中点,
∴QP=PD=t,
∴AD=3AQ=3t=24,
解得:t=8.
∴当t为8秒时,点P恰好是QD的中点.
②如图所示,点P在点D左侧时,
∵点Q是AP的中点,AP=2t,
∴,PD=AD﹣AP=24﹣2t,
∵AQ=2PD,
∴t=2(24﹣2t),
∴t=48﹣4t,
解得:,
∴当t为秒时,AQ=2PD.
如图所示,点P在点D右侧时,
∵点Q是AP的中点,AP=2t,
∴,PD=AP﹣AD=2t﹣24,
∵AQ=2PD,
∴t=2(2t﹣24),
∴t=4t﹣48,
解得:t=16,
∴当t为16秒时,AQ=2PD.
综上所述,t为秒或16秒时,AQ=2PD.
【点评】本题考查了一元一次方程的应用,线段的和差,线段的大小比较,掌握解一元一次方程的方法,线段的和差计算,线段的大小比较方法是解题的关键.
11.如图1,已知射线OA,OB,OC,OD.
(1)若,且∠AOC=80°,求∠AOD的度数.
(2)若∠AOD=120°,OB是∠AOC的平分线,OC是∠AOD的平分线,求∠BOD的度数.
(3)若∠AOB:∠BOC:∠COD=2:3:4,OM,ON分别是∠AOB和∠COD的平分线,∠MON=90°,求∠AOD的度数.
(4)定义:从∠α(45°<α<90°)的顶点出发,在角的内部作一条射线,若该射线将∠α分得的两个角中有一个角与∠α互为余角,则称该射线为∠α的“分余线”.
①若OC平分∠BOD,且OC为∠BOD的“分余线”,则∠BOD= 60° ;
②如图2,∠AOD=160°,OB为∠AOC的平分线,在∠COD的内部作射线OP,使∠POD=2∠COP,当OC为∠BOP的“分余线”时,求∠COD的度数.
【答案】(1)100°;
(2)90°;
(3)135°;
(4)①60°;
②105°或60°.
【分析】(1)根据题意,得到∠BOC=60°,从而得到∠AOD的度数;
(2)利用角平分线,得到∠AOB=∠BOC,∠AOC=∠COD,从而得到结果;
(3)利用角之间的比例关系,设∠AOB=2x°,∠BOC=3x°,∠COD=4x°,利用角平分线,从而得到结果;
(4)①根据新定义,∠BOC+∠BOD=90°,结合角平分线得到∠BOC=∠COD,从而求得结果;
②根据题意,OC为∠BOP的“分余线”,分别讨论∠BOC+∠BOP=90°或∠COP+∠BOP=90°这两种情况,从而得到结果.
【解答】解:(1)∵∠BOC∠AOC,∠AOC=80°,
∴∠BOC=60°,
∴∠AOB=∠AOC﹣∠BOC=20°,
∵∠AOB=∠COD,
∴∠COD=20°,
∴∠AOD=∠AOC+∠COD=100°;
(2)∵OB是∠AOC的平分线,
∴∠AOB=∠BOC,
∵OC是∠AOD的平分线,
∴∠AOC=∠COD,
∴∠COD∠AOD=60°,
∵∠BOC=30°,
∴∠BOD=∠BOC+∠COD=90°;
(3)如图:
∵∠AOB:∠BOC:∠COD=2:3:4,
∴设∠AOB=2x°,∠BOC=3x°,∠COD=4x°,
∵OM,ON分别是∠AOB和∠COD的平分线,
∴∠MOB,,
∵∠MON=90°,
∴∠MOB+∠BOC+∠CON=90°,
即:x+3x+2x=90,
解得:x=15,
∴∠AOD=∠AOB+∠BOC+∠COD=9x°=135°;
(4)①∵OC平分∠BOD,且OC为∠BOD的“分余线”,
∴∠BOC=∠COD,且∠BOC+∠BOD=90°,
∴∠BOC+2∠BOC=90°,
∴∠BOC=30°,
∴∠BOC=60°,
故答案为:60°;
②如图2,
∵OB为∠AOC的平分线,
∴∠AOB=∠BOC,
∵OC为∠BOP的“分余线”,
∴∠BOC+∠BOP=90°或∠COP+∠BOP=90°,
若∠BOC+∠BOP=90°时,
令∠BOC=x°,
则∠AOB=x°,∠BOP=90°﹣x°,
∴∠COP=90°﹣2x°,
∵∠POD=2∠COP,
∴∠POD=2(90°﹣2x°),
∵∠AOD=160°,
∴∠AOB+∠BOP+∠POD=160°,
∴x+90﹣x+2(90﹣2x)=160,
解得x=27.5,
∴∠COD=∠AOD﹣2∠AOB=160°﹣2×27.5°=105°;
若∠COP+∠BOP=90°时,
令∠COP=x°,则∠BOP=90°﹣x°,
∴∠AOB=90°﹣2x°,∠POD=2x°,
∵∠AOB+∠BOP+∠POD=160°,
∴(90°﹣2x°)+(90°﹣x°)+2x°=160°,
解得:x=20,
∴∠COD=∠COP+∠POD=60°.
综上所述,∠COD为105°或60°.
【点评】本题考查了角平分性质,互为余角的概念,以及新定义的“分余线”的应用,关键是对新定义的理解和正确应用.
第1页(共1页)
一、选择题
1.下列图形中是圆柱的是( )
A. B.
C. D.
2.如图,利用量角器可知∠AOB的度数为( )
A.150° B.30° C.40° D.60°
3.已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
4.如图,A,B位于数轴上原点两侧,且OB=2OA.若点B表示的数是6,则点A表示的数是( )
A.﹣2 B.﹣3 C.﹣4 D.﹣5
5.“争创全国文明卫生城市,让文明成为我县人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( )
A.文 B.明 C.卫 D.生
6.互不重合的A、B、C三点在同一直线上,已知AB=2a,AC=a+6,BC=3a+1,则这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
二、填空题
7.如图,将一副三角板的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= °.
8.如图,点O在直线AB上,OD是∠BOC的平分线,若∠AOC=140°,则∠AOD的度数为 .
三、解答题
9.根据以下素材,探索完成任务.
时钟里的数学问题
素材1 时钟是我们日常生活中常用的生活用品,钟表上的时针和分针都绕其轴心旋转,如图1,表盘中1~12均匀分布,分针60分钟转动一周是360°时针60分钟移动一周的是30°,这样,分针转速为每分钟转6度,时针转速为每分钟转0.5度.
素材2 当时钟显示10:10时(如图2),时针与分针所成角度多少度?解决这个问题,可以先考虑10:00时,时针与分针所成角度为60°;从10:00到10:10,分针转动的角度为10×6=60°时针转动的角度为10×0.5=5°,60+60﹣5=115°因此10点10分时,时针与分针所成角度是115°.
素材3 当时针和分针所成角度180°时,我们将这样的时刻称为“美妙时刻”.如图3,当时钟显示6:00时,此时,时针和分针所成角度180°因此6:00就是一个美妙时刻.
解决问题
任务1 当时钟显示11:10分时,求时针与分针所成角度.
任务2 时钟显示1:00时,时针与分针所成角度为30°在1:00到1:30的30分钟内,小明发现存在着时针和分针垂直的情况,请求出此时的时刻.
任务3 6:00之后的下一个美妙时刻是 .一天24个小时内,共有 个美妙时刻.
10.如图,A,B,C,D四点在同一直线上.
(1)若AB=CD,比较线段的大小:AC BD(填“>”“<”或“=”).
(2)在(1)的基础上,若,且AC=16,求AD的长.
(3)若AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,求BC的长.
(4)若线段AD被点B,C分成了长度比为2:3:4的三部分,且AB的中点M和CD的中点N之间的距离是18,求AD的长.
(5)若AD=24,动点P从A出发,以每秒2个单位的速度沿射线AD方向运动,运动时间为t(t>0)秒,点Q为AP的中点.
①当t为何值时,点P恰好是QD的中点?
②当t为何值时,AQ=2PD?
11.如图1,已知射线OA,OB,OC,OD.
(1)若,且∠AOC=80°,求∠AOD的度数.
(2)若∠AOD=120°,OB是∠AOC的平分线,OC是∠AOD的平分线,求∠BOD的度数.
(3)若∠AOB:∠BOC:∠COD=2:3:4,OM,ON分别是∠AOB和∠COD的平分线,∠MON=90°,求∠AOD的度数.
(4)定义:从∠α(45°<α<90°)的顶点出发,在角的内部作一条射线,若该射线将∠α分得的两个角中有一个角与∠α互为余角,则称该射线为∠α的“分余线”.
①若OC平分∠BOD,且OC为∠BOD的“分余线”,则∠BOD= ;
②如图2,∠AOD=160°,OB为∠AOC的平分线,在∠COD的内部作射线OP,使∠POD=2∠COP,当OC为∠BOP的“分余线”时,求∠COD的度数.
第4章 图形的认识
参考答案与试题解析
一、选择题
1.下列图形中是圆柱的是( )
A. B.
C. D.
【答案】B
【分析】根据圆柱体的概念和定义,圆柱体的上下两个底面是圆形,平行且相等.
【解答】解:根据以上分析B为圆柱体.
故选:B.
【点评】本题考查的是圆柱的定义,关键点在于:圆柱体上下底面是圆形且平行和相等的.
2.如图,利用量角器可知∠AOB的度数为( )
A.150° B.30° C.40° D.60°
【答案】B
【分析】利用对顶角相等即可求得.
【解答】解:因为对顶角相等,
所以∠AOB的度数为30°,
故选:B.
【点评】本题考查的是对顶角的度数,解题的关键是会识图,了解对顶角相等.
3.已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
【答案】B
【分析】根据余角的定义,两个锐角和为90°的角互余.
【解答】解:由题意得:∠α=25°30′,
故其余角为(90°﹣∠α)=64°30′.
故选:B.
【点评】本题考查的知识点是两个角的互余,互余的两个角的和为90°.
4.如图,A,B位于数轴上原点两侧,且OB=2OA.若点B表示的数是6,则点A表示的数是( )
A.﹣2 B.﹣3 C.﹣4 D.﹣5
【答案】B
【分析】根据条件求出OA的长度,点A在原点的左侧,点A为负数,从而得出答案.
【解答】解:∵点B表示的数是6,
∴OB=6,
∵OB=2OA,
∴OA=3,
∴点A表示的数为﹣3,
故选:B.
【点评】本题考查了实数与数轴,根据条件求出OA的长度是解题的关键.
5.“争创全国文明卫生城市,让文明成为我县人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是( )
A.文 B.明 C.卫 D.生
【答案】B
【分析】根据正方体的表面展开图找相对面的方法:“Z”字两端是对面,即可解答.
【解答】解:把展开图折叠成正方体后,“城”字对面的字是明,
故选:B.
【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.
6.互不重合的A、B、C三点在同一直线上,已知AB=2a,AC=a+6,BC=3a+1,则这三点的位置关系是( )
A.点A在B、C两点之间 B.点B在A、C两点之间
C.点C在A、B两点之间 D.无法确定
【答案】B
【分析】用假设法分别计算各选项中的a值,再根据a>0判断即可.
【解答】解:∵AC=a+6,BC=3a+1,AB=2a,A、B、C三点互不重合,
∴a>0,
若点A在B、C之间,
则AB+AC=BC,
即2a+a+6=3a+1,
此时无解,
故此情况不存在,
若点B在A、C之间,
则BC+AB=AC,
3a+1+2a=a+6,
a,
故此情况存在,
若点C在A、B之间,
则BC+AC=AB,
即3a+1+a+6=2a,
a,
故此情况不存在,
∵互不重合的A、B、C三点在同一直线上,
故选:B.
【点评】本题主要考查两点间的距离及整式的加减,分类讨论和反证法的应用是解题的关键.
二、填空题
7.如图,将一副三角板的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= 30 °.
【答案】见试题解答内容
【分析】从图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解.
【解答】解:∵∠AOB=∠COD=90°,∠AOD=150°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.
故答案为:30.
【点评】此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.
8.如图,点O在直线AB上,OD是∠BOC的平分线,若∠AOC=140°,则∠AOD的度数为 160° .
【答案】见试题解答内容
【分析】根据邻补角定义求得∠BOC的度数,再根据角平分线定义即可求得答案.
【解答】解:∵∠AOC=140°,
∴∠BOC=180°﹣140°=40°,
∵OD是∠BOC的平分线,
∴∠BOD∠BOC=20°,
∴∠AOD=180°﹣20°=160°,
故答案为:160°.
【点评】本题主要考查角平分线的定义,此为几何中基础且重要知识点,必须熟练掌握.
三、解答题
9.根据以下素材,探索完成任务.
时钟里的数学问题
素材1 时钟是我们日常生活中常用的生活用品,钟表上的时针和分针都绕其轴心旋转,如图1,表盘中1~12均匀分布,分针60分钟转动一周是360°时针60分钟移动一周的是30°,这样,分针转速为每分钟转6度,时针转速为每分钟转0.5度.
素材2 当时钟显示10:10时(如图2),时针与分针所成角度多少度?解决这个问题,可以先考虑10:00时,时针与分针所成角度为60°;从10:00到10:10,分针转动的角度为10×6=60°时针转动的角度为10×0.5=5°,60+60﹣5=115°因此10点10分时,时针与分针所成角度是115°.
素材3 当时针和分针所成角度180°时,我们将这样的时刻称为“美妙时刻”.如图3,当时钟显示6:00时,此时,时针和分针所成角度180°因此6:00就是一个美妙时刻.
解决问题
任务1 当时钟显示11:10分时,求时针与分针所成角度.
任务2 时钟显示1:00时,时针与分针所成角度为30°在1:00到1:30的30分钟内,小明发现存在着时针和分针垂直的情况,请求出此时的时刻.
任务3 6:00之后的下一个美妙时刻是 7: .一天24个小时内,共有 22 个美妙时刻.
【答案】任务一:85°;
任务二:1:;
任务三:7:,22.
【分析】任务一:利用时针与分针所成角度=30°+分针转过的度数﹣时针转过的度数,即可求出结论;
任务二:设1点x分时,时针与分针垂直,利用分针转过的度数﹣(时针转过的度数+30°)=90°,可列出关于x的一元一次方程,解之即可得出结论;
任务三:设再经过y分钟,时针和分针所成角度第一次为180°,利用分针转过的度数﹣时针转过的度数=360°,可列出关于y的一元一次方程,解之可得出6:00之后的下一个美妙时刻是7:;设从0:00开始经过m分钟,时针和分针所成角度为180°,利用分针转过的度数﹣时针转过的度数=180°的奇数倍,可列出关于m的一元一次方程,解之可得出m,结合m≤60×24,可列出关于n的一元一次不等式,解之可得出n的取值范围,再结合n为正整数,即可得出结论.
【解答】解:任务一:30°+10×6°﹣10×0.5°=85°.
答:当时钟显示11:10时,时针与分针所成角度为85°;
任务二:设1点x分时,时针与分针垂直,
根据题意得:6x﹣(30+0.5x)=90,
解得:x.
答:此时的时刻为1:;
任务三:设再经过y分钟,时针和分针所成角度第一次为180°,
根据题意得:6y﹣0.5y=360,
解得:y60,
∴6:00之后的下一个美妙时刻是7:;
从0:00开始经过m分钟,时针和分针所成角度为180°,
根据题意得:6m﹣0.5m=180(2n﹣1)(n为正整数),
解得:m,
∵m≤60×24,
∴60×24,
解得:n,
又∵n为正整数,
∴n的最大值为22,
∴一天24个小时内,共有22个美妙时刻.
故答案为:7:,22.
【点评】本题考查了一元一次方程的应用、钟面角、分数的除法以及解一元一次不等式,找准等量关系,正确列出一元一次方程是解题的关键.
10.如图,A,B,C,D四点在同一直线上.
(1)若AB=CD,比较线段的大小:AC = BD(填“>”“<”或“=”).
(2)在(1)的基础上,若,且AC=16,求AD的长.
(3)若AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,求BC的长.
(4)若线段AD被点B,C分成了长度比为2:3:4的三部分,且AB的中点M和CD的中点N之间的距离是18,求AD的长.
(5)若AD=24,动点P从A出发,以每秒2个单位的速度沿射线AD方向运动,运动时间为t(t>0)秒,点Q为AP的中点.
①当t为何值时,点P恰好是QD的中点?
②当t为何值时,AQ=2PD?
【答案】(1)=;
(2)20;
(3)2;
(4)27;
(5)①8秒;
②秒或16秒.
【分析】(1)根据题意,AB=CD,则AB+BC=CD+BC,由线段的大小比较进而得出答案;
(2)根据题意,,AC=16,可得出BC的长,进而得出AB的长,由(1)可知AB=CD,进而得出AD的长;
(3)由题意可知,AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,可求出AB,AC的长,根据BC=AC﹣AB,即可得出答案;
(4)由题意可知,M是线段AB的中点,AB:BC:CD=2:3:4,得出AM=BM,设AM=BM=x,从而得出AB=2x,BC=3x,CD=4x,进而得出AD=9x,再根据已知N是线段CD的中点,MN=18,得出CN=DN=2x,列出方程:x+3x+2x=18,解一元一次方程求出x的值,进而得出答案;
(5)①根据题意可得AP=2t,,再根据已知点P是QD的中点,所以得出QP=PD=t,进而得出AD=3AQ=3t=24,求出t值即可;
②分两种情况:点P在点D的左侧和右侧,根据如图可得,PD=AD﹣AP=24﹣2t,或PD=AP﹣AD=2t﹣24,再根据AQ=2PD,列出关于t的方程,进而得出t的值.
【解答】解:(1)∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD.
故答案为:=;
(2)∵,AC=16,
∴,
∴AB=AC﹣BC=16﹣12=4,
在(1)的基础上,∵AB=CD,
∴CD=4,
∴AD=AC+CD=16+4=20.
(3)如图所示:
由题意可知,AD=12,点B是线段AD靠近点A的三等分点,点C是线段AD的中点,
∴,,
∴BC=AC﹣AB=6﹣4=2;
(4)如图所示:
∵M是线段AB的中点,AB:BC:CD=2:3:4,
∴AM=BM,
设AM=BM=x,
∴AB=2x,BC=3x,CD=4x,
∴AD=AB+BC+CD=2x+3x+4x=9x.
∵N是线段CD的中点,MN=18,
∴CN=DN=2x,
∴x+3x+2x=18,
解得:x=3,
∴AD=9x=9×3=27.
(5)①如图所示:
∵点Q是AP的中点,AP=2t,
∴,
又∵点P是QD的中点,
∴QP=PD=t,
∴AD=3AQ=3t=24,
解得:t=8.
∴当t为8秒时,点P恰好是QD的中点.
②如图所示,点P在点D左侧时,
∵点Q是AP的中点,AP=2t,
∴,PD=AD﹣AP=24﹣2t,
∵AQ=2PD,
∴t=2(24﹣2t),
∴t=48﹣4t,
解得:,
∴当t为秒时,AQ=2PD.
如图所示,点P在点D右侧时,
∵点Q是AP的中点,AP=2t,
∴,PD=AP﹣AD=2t﹣24,
∵AQ=2PD,
∴t=2(2t﹣24),
∴t=4t﹣48,
解得:t=16,
∴当t为16秒时,AQ=2PD.
综上所述,t为秒或16秒时,AQ=2PD.
【点评】本题考查了一元一次方程的应用,线段的和差,线段的大小比较,掌握解一元一次方程的方法,线段的和差计算,线段的大小比较方法是解题的关键.
11.如图1,已知射线OA,OB,OC,OD.
(1)若,且∠AOC=80°,求∠AOD的度数.
(2)若∠AOD=120°,OB是∠AOC的平分线,OC是∠AOD的平分线,求∠BOD的度数.
(3)若∠AOB:∠BOC:∠COD=2:3:4,OM,ON分别是∠AOB和∠COD的平分线,∠MON=90°,求∠AOD的度数.
(4)定义:从∠α(45°<α<90°)的顶点出发,在角的内部作一条射线,若该射线将∠α分得的两个角中有一个角与∠α互为余角,则称该射线为∠α的“分余线”.
①若OC平分∠BOD,且OC为∠BOD的“分余线”,则∠BOD= 60° ;
②如图2,∠AOD=160°,OB为∠AOC的平分线,在∠COD的内部作射线OP,使∠POD=2∠COP,当OC为∠BOP的“分余线”时,求∠COD的度数.
【答案】(1)100°;
(2)90°;
(3)135°;
(4)①60°;
②105°或60°.
【分析】(1)根据题意,得到∠BOC=60°,从而得到∠AOD的度数;
(2)利用角平分线,得到∠AOB=∠BOC,∠AOC=∠COD,从而得到结果;
(3)利用角之间的比例关系,设∠AOB=2x°,∠BOC=3x°,∠COD=4x°,利用角平分线,从而得到结果;
(4)①根据新定义,∠BOC+∠BOD=90°,结合角平分线得到∠BOC=∠COD,从而求得结果;
②根据题意,OC为∠BOP的“分余线”,分别讨论∠BOC+∠BOP=90°或∠COP+∠BOP=90°这两种情况,从而得到结果.
【解答】解:(1)∵∠BOC∠AOC,∠AOC=80°,
∴∠BOC=60°,
∴∠AOB=∠AOC﹣∠BOC=20°,
∵∠AOB=∠COD,
∴∠COD=20°,
∴∠AOD=∠AOC+∠COD=100°;
(2)∵OB是∠AOC的平分线,
∴∠AOB=∠BOC,
∵OC是∠AOD的平分线,
∴∠AOC=∠COD,
∴∠COD∠AOD=60°,
∵∠BOC=30°,
∴∠BOD=∠BOC+∠COD=90°;
(3)如图:
∵∠AOB:∠BOC:∠COD=2:3:4,
∴设∠AOB=2x°,∠BOC=3x°,∠COD=4x°,
∵OM,ON分别是∠AOB和∠COD的平分线,
∴∠MOB,,
∵∠MON=90°,
∴∠MOB+∠BOC+∠CON=90°,
即:x+3x+2x=90,
解得:x=15,
∴∠AOD=∠AOB+∠BOC+∠COD=9x°=135°;
(4)①∵OC平分∠BOD,且OC为∠BOD的“分余线”,
∴∠BOC=∠COD,且∠BOC+∠BOD=90°,
∴∠BOC+2∠BOC=90°,
∴∠BOC=30°,
∴∠BOC=60°,
故答案为:60°;
②如图2,
∵OB为∠AOC的平分线,
∴∠AOB=∠BOC,
∵OC为∠BOP的“分余线”,
∴∠BOC+∠BOP=90°或∠COP+∠BOP=90°,
若∠BOC+∠BOP=90°时,
令∠BOC=x°,
则∠AOB=x°,∠BOP=90°﹣x°,
∴∠COP=90°﹣2x°,
∵∠POD=2∠COP,
∴∠POD=2(90°﹣2x°),
∵∠AOD=160°,
∴∠AOB+∠BOP+∠POD=160°,
∴x+90﹣x+2(90﹣2x)=160,
解得x=27.5,
∴∠COD=∠AOD﹣2∠AOB=160°﹣2×27.5°=105°;
若∠COP+∠BOP=90°时,
令∠COP=x°,则∠BOP=90°﹣x°,
∴∠AOB=90°﹣2x°,∠POD=2x°,
∵∠AOB+∠BOP+∠POD=160°,
∴(90°﹣2x°)+(90°﹣x°)+2x°=160°,
解得:x=20,
∴∠COD=∠COP+∠POD=60°.
综上所述,∠COD为105°或60°.
【点评】本题考查了角平分性质,互为余角的概念,以及新定义的“分余线”的应用,关键是对新定义的理解和正确应用.
第1页(共1页)
同课章节目录
