第3章 一次方程(组)(新课预习.培优卷)(含解析)-2025-2026学年七年级上册数学湘教版(2024)
文档属性
| 名称 | 第3章 一次方程(组)(新课预习.培优卷)(含解析)-2025-2026学年七年级上册数学湘教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 211.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 12:34:42 | ||
图片预览




文档简介
第3章 一次方程(组)
一、选择题
1.关于x的一元一次方程2x+m=6的解为x=1,则m的值为( )
A.3 B.4 C.5 D.6
2.某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.设购买A,B两种劳动工具的件数分别为x,y,那么下面列出的方程组中正确的是( )
A.
B.
C.
D.
3.《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完.问:城中有多少户人家?( )
A.55 B.65 C.75 D.85
二、填空题
4.已知是方程ax+by=3的解,则代数式2a+4b+5的值为 .
三、解答题
5.体育与健康是学校素质教育的重要组成部分,为活跃校园氛围,培养学生团队合作的精神,某校计划开展七年级趣味运动会.
【基础设问】
(1)七年级一班计划购买甲、乙两种型号的羽毛球拍共30副,已知甲种型号的羽毛球拍每副50元,乙种型号的羽毛球拍每副40元,若购买甲、乙两种型号的羽毛球拍共花费1360元,求甲、乙两种型号的羽毛球拍各买了多少副.
(2)王老师组织七年级二班的学生打扫操场,其中男生25人,女生23人,如果让男生单独打扫,需要5h,如果让女生单独打扫,需要7.5h.如果让男生、女生一起打扫1h,再由男生单独完成剩余的部分,求男生共打扫了多长时间.
【能力设问】
(3)东东和乐乐在操场练习跑步,环形跑道周长为400m,乐乐的速度为6m/s,东东的速度为4m/s.
①若他俩同时同地背向跑,则多少秒后两人第一次相遇?
②若他俩同时同向跑,乐乐在东东前面20m,则多少秒后两人第一次相遇?
(4)趣味运动会表演需要使用一种圆柱形小鼓,在劳动课上杨老师带领七年级五班50名学生进行制作,该班男生人数比女生人数少6人,并且每名学生每小时可制作2个鼓身或剪6个鼓面.求男生和女生各有多少人.
追问1:老师组织全班学生制作小鼓,要求一个鼓身配两个鼓面,为了使每小时制作的鼓身与剪出的鼓面刚好配套,应该分配多少名学生制作鼓身?多少名学生剪鼓面?
追问2:若想1小时制作90个小鼓,且制作的鼓身与剪出的鼓面刚好配套,应再加入多少名学生?
【拓展设问】
(5)在足球趣味赛中,共赛了17轮(即每队均需参赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.
①在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
②在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种.
6.双十一期间,大润发超市各个区域都有促销活动,小文一家去逛该超市,准备购买牛奶,根据以下素材,探索完成任务.
生活中的数学问题
素材1 超市有A品牌牛奶大瓶和小瓶两种型号,大瓶牛奶每瓶15元,小瓶牛奶每瓶10元.
素材2 小文去超市购买了8瓶A品牌牛奶,共花了89元.
素材3 过了几天,小明去超市,发现原价每瓶15元的B品牌牛奶“买二送一”促销.
买 2 送 1B品牌牛奶促销套装温馨提醒: 1.买两瓶送一瓶,同款B品牌牛奶; 2.套装不可拆开单卖.
问题解决
任务1 小文妈妈说:按原价购买,不可能是89元!请说明小文妈妈这样说的理由.
任务2 小文看了一下购物小票,发现有1瓶是“会员打6折限购1瓶”的大瓶牛奶,请问小文购买了大瓶牛奶和小瓶牛奶各多少瓶?
任务3 小明按原价购买A品牌大、小瓶牛奶若干瓶,同时购买B品牌促销套装若干套,一共花费210元.其中A品牌大瓶牛奶占所有牛奶瓶数(包括促销套装中赠送牛奶)的.求小明A品牌大瓶牛奶买了多少瓶?
7.根据以下素材,探索完成任务.
如何设计板材裁切方案?
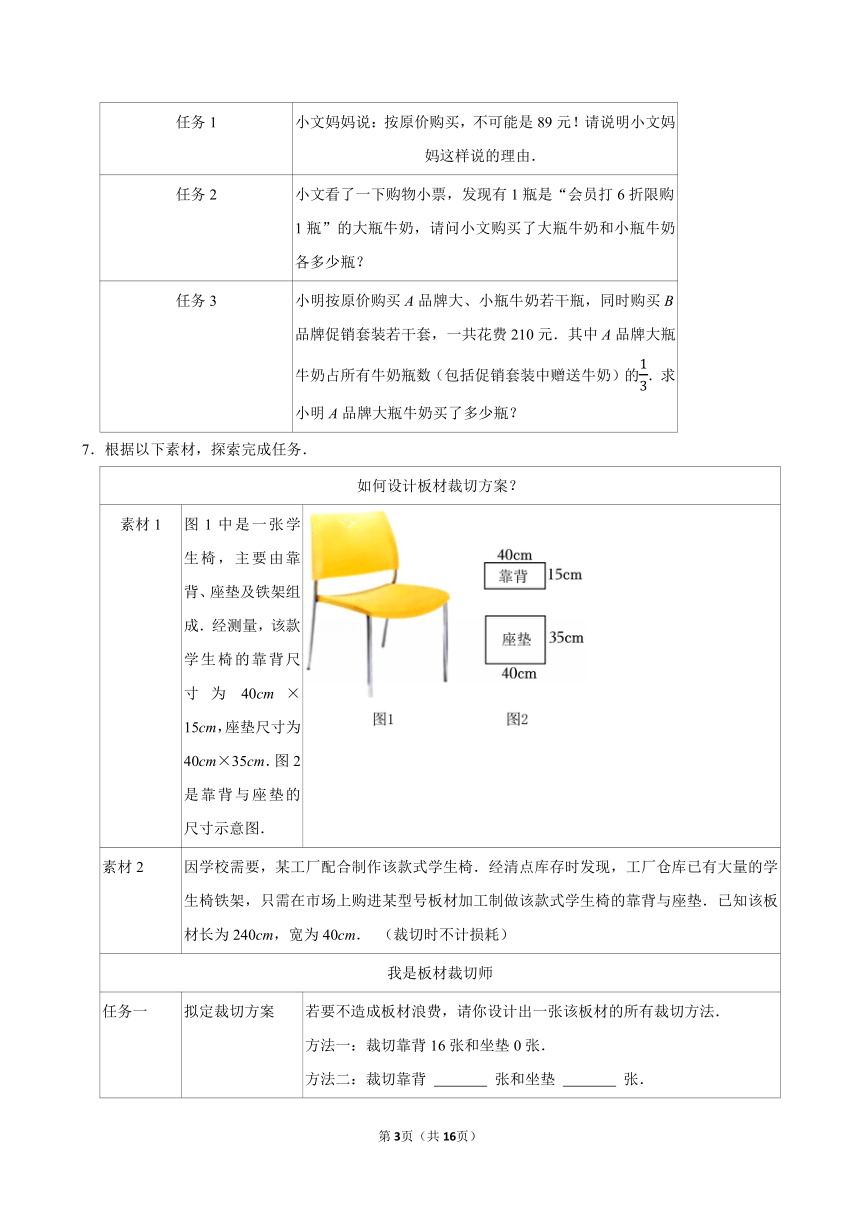
素材1 图1中是一张学生椅,主要由靠背、座垫及铁架组成.经测量,该款学生椅的靠背尺寸为40cm×15cm,座垫尺寸为40cm×35cm.图2是靠背与座垫的尺寸示意图.
素材2 因学校需要,某工厂配合制作该款式学生椅.经清点库存时发现,工厂仓库已有大量的学生椅铁架,只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为240cm,宽为40cm. (裁切时不计损耗)
我是板材裁切师
任务一 拟定裁切方案 若要不造成板材浪费,请你设计出一张该板材的所有裁切方法. 方法一:裁切靠背16张和坐垫0张. 方法二:裁切靠背 张和坐垫 张. 方法三:裁切靠背 张和坐垫 张.
任务二 确定搭配数量 若该工厂购进50张该型号板材,能制作成多少张学生椅?
任务三 解决实际问题 现需要制作700张学生椅,该工厂仓库现有1张座垫和11张靠背,还需要购买该型号板材多少张(恰好全部用完)?并给出一种裁切方案.
8.解方程组:.
9.小明乘家门口的公共汽车赶往火车站,如果乘公共汽车一直到火车站,到火车站时火车正好开出.于是在公共汽车行驶了一半路程时,小明马上下车,并立即乘出租车前往火车站.出租车的速度是公共汽车速度的2倍,结果在火车开车前15min到达火车站.已知公共汽车的平均速度30km/h,那么小明家到火车站的路程是多少千米?
10.某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召,积极扩大粮食生产规模,计划用基地的甲、乙两区农田进行油菜试种,甲区的农田比乙区的农田多10000亩,甲区农田的80%和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同.
(1)求甲、乙两区各有农田多少亩?
(2)在甲、乙两区适宜试种的农田全部种上油菜后,为加强油菜的虫害治理,基地派出一批性能相同的无人机,对试种农田喷洒除虫药,由于两区地势差别,派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),喷洒任务完成后,发现派往甲区的每架次无人机比乙区的平均多喷洒亩,求派往甲区每架次无人机平均喷洒多少亩?
第3章 一次方程(组)
参考答案与试题解析
一、选择题
1.关于x的一元一次方程2x+m=6的解为x=1,则m的值为( )
A.3 B.4 C.5 D.6
【答案】B
【分析】将x=1代入方程2x+m=6,得到关于m的一元一次方程,解方程即可求出m的值.
【解答】解:∵关于x的一元一次方程2x+m=6的解为x=1,
∴2+m=6,
解得m=4.
故选:B.
【点评】本题考查了一元一次方程的解的定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.
2.某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.设购买A,B两种劳动工具的件数分别为x,y,那么下面列出的方程组中正确的是( )
A.
B.
C.
D.
【答案】A
【分析】利用总价=单价×数量,结合学校用1580元购进A,B两种劳动工具共145件,可列出关于x,y的二元一次方程组,此题得解.
【解答】解:∵购进A,B两种劳动工具共145件,
∴x+y=145;
∵A,B两种劳动工具每件分别为10元,12元.且购买这批劳动工具共花费1580元,
∴10x+12y=1580,
∴根据题意可列出方程组.
故选:A.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
3.《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完.问:城中有多少户人家?( )
A.55 B.65 C.75 D.85
【答案】C
【分析】设城中有x户人家,根据“今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完”,即可得出关于x的一元一次方程,解之即可得出结论.
【解答】解:设城中有x户人家,
依题意,得:xx=100,
解得:x=75.
故选:C.
【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
二、填空题
4.已知是方程ax+by=3的解,则代数式2a+4b+5的值为 11 .
【答案】11.
【分析】把x与y的值代入方程计算得到a+2b的值,原式变形后代入计算即可求出值.
【解答】解:把代入ax+by=3得:a+2b=3,
则原式=2(a+2b)+5
=2×3+5
=6+5
=11.
故答案为:11.
【点评】此题考查了二元一次方程的解,以及代数式求值,方程的解即为能使方程左右两边相等的未知数的值.
三、解答题
5.体育与健康是学校素质教育的重要组成部分,为活跃校园氛围,培养学生团队合作的精神,某校计划开展七年级趣味运动会.
【基础设问】
(1)七年级一班计划购买甲、乙两种型号的羽毛球拍共30副,已知甲种型号的羽毛球拍每副50元,乙种型号的羽毛球拍每副40元,若购买甲、乙两种型号的羽毛球拍共花费1360元,求甲、乙两种型号的羽毛球拍各买了多少副.
(2)王老师组织七年级二班的学生打扫操场,其中男生25人,女生23人,如果让男生单独打扫,需要5h,如果让女生单独打扫,需要7.5h.如果让男生、女生一起打扫1h,再由男生单独完成剩余的部分,求男生共打扫了多长时间.
【能力设问】
(3)东东和乐乐在操场练习跑步,环形跑道周长为400m,乐乐的速度为6m/s,东东的速度为4m/s.
①若他俩同时同地背向跑,则多少秒后两人第一次相遇?
②若他俩同时同向跑,乐乐在东东前面20m,则多少秒后两人第一次相遇?
(4)趣味运动会表演需要使用一种圆柱形小鼓,在劳动课上杨老师带领七年级五班50名学生进行制作,该班男生人数比女生人数少6人,并且每名学生每小时可制作2个鼓身或剪6个鼓面.求男生和女生各有多少人.
追问1:老师组织全班学生制作小鼓,要求一个鼓身配两个鼓面,为了使每小时制作的鼓身与剪出的鼓面刚好配套,应该分配多少名学生制作鼓身?多少名学生剪鼓面?
追问2:若想1小时制作90个小鼓,且制作的鼓身与剪出的鼓面刚好配套,应再加入多少名学生?
【拓展设问】
(5)在足球趣味赛中,共赛了17轮(即每队均需参赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.
①在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
②在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种.
【答案】(1)甲种型号羽毛球拍买了16副,乙种型号的羽毛球拍买了14副;
(2)小时;
(3)①40秒;
②190秒;
(4)男生有22人,女生有28人;
追问1.应分配30名学生制作鼓身,则20名学生剪鼓面;
追问2.应再加入25名学生;
(5)①3场;
②小虎足球队踢负场数的情况有3种,分别是1,5,7场.
【分析】(1)设甲种型号羽毛球拍买了z副,则乙种型号的羽毛球拍买了(30﹣z)副,由题意得出方程50z+40(30﹣z)=1360,根据解一元一次方程的方法求出z的值,进而得出答案;
(2)设男生共打扫了w小时,由题意列出方程:,根据解一元一次方程的方法求解即可;
(3)①设t秒后两人第一次相遇,由题意列出方程:6t+4t=400,根据解一元一次方程的方法求解即可;
②设b秒后两人第一次相遇,根据题意列出方程:6b+20﹣4b=400,根据解一元一次方程的方法求解即可.
(4)设男生有x人,女生有(50﹣x)人,根据题意列出方程:x+6=50﹣x,根据解一元一次方程的方法求出x的值,进而得出答案;
追问1.设分配a名学生制作鼓身,则(50﹣a)名学生剪鼓面,由题意可列出方程:2×2a=6(50﹣a),根据解一元一次方程的方法求出a的值,进而得出答案;
追问2.根据追问1可知,50名学生1小时可制作60个小鼓,则若要每小时制作90个小鼓,需要增加一半的人数.
(5)①设小虎队胜了x场,平了y场,则负了y场,由题意列出方程组:,根据解二元一次方程组的方法求解即可;
②设小虎队胜了m场,负了n场,踢平场数是踢负场数的k倍(k为整数),由题意列出方程组:,得出,由n为正整数,进而得出答案.
【解答】解:(1)设甲种型号羽毛球拍买了z副,则乙种型号的羽毛球拍买了(30﹣z)副,
由题意,得50z+40(30﹣z)=1360,
解得:z=16,
∴30﹣z=30﹣16=14.
答:甲种型号羽毛球拍买了16副,乙种型号的羽毛球拍买了14副.
(2)设男生共打扫了w小时,
由题意,得,
解得:.
答:男生共打扫了小时.
(3)①设t秒后两人第一次相遇,
由题意,得6t+4t=400,
解得:t=40.
答:40秒后两人第一次相遇;
②设b秒后两人第一次相遇,
由题意,得6b+20﹣4b=400,
解得:b=190.
答:190秒后两人第一次相遇.
(4)设男生有x人,女生有(50﹣x)人,
由题意,得x+6=50﹣x,
解得:x=22,
∴50﹣x=50﹣22=28.
答:男生有22人,女生有28人.
追问1.设分配a名学生制作鼓身,则(50﹣a)名学生剪鼓面,
由题意,得2×2a=6(50﹣a),
解得:a=30,
∴50﹣a=50﹣30=20.
答:应分配30名学生制作鼓身,则20名学生剪鼓面;
追问2.由追问1可知,分配30名学生制作鼓身,20名学生剪鼓面,
则1小时可制作小鼓30×2=60(个),还需制作90﹣60=30(个)小鼓,
∴50÷2=25(人).
答:应再加入25名学生.
(5)①设小虎队胜了x场,平了y场,则负了y场,
由题意,得,
解得:.
答:该队胜了3场.
②设小虎队胜了m场,负了n场,踢平场数是踢负场数的k倍(k为整数),
由题意,得,
解得:,
又∵n为正整数,
∴,,.
答:小虎足球队踢负场数的情况有3种,分别是1,5,7场.
【点评】本题考查了一元一次方程的应用,二元一次方程组的应用,根据题意,找准等量关系,正确列出方程,方程组是解题的关键.
6.双十一期间,大润发超市各个区域都有促销活动,小文一家去逛该超市,准备购买牛奶,根据以下素材,探索完成任务.
生活中的数学问题
素材1 超市有A品牌牛奶大瓶和小瓶两种型号,大瓶牛奶每瓶15元,小瓶牛奶每瓶10元.
素材2 小文去超市购买了8瓶A品牌牛奶,共花了89元.
素材3 过了几天,小明去超市,发现原价每瓶15元的B品牌牛奶“买二送一”促销.
B品牌牛奶促销套装温馨提醒: 1.买两瓶送一瓶,同款B品牌牛奶; 2.套装不可拆开单卖.
问题解决
任务1 小文妈妈说:按原价购买,不可能是89元!请说明小文妈妈这样说的理由.
任务2 小文看了一下购物小票,发现有1瓶是“会员打6折限购1瓶”的大瓶牛奶,请问小文购买了大瓶牛奶和小瓶牛奶各多少瓶?
任务3 小明按原价购买A品牌大、小瓶牛奶若干瓶,同时购买B品牌促销套装若干套,一共花费210元.其中A品牌大瓶牛奶占所有牛奶瓶数(包括促销套装中赠送牛奶)的.求小明A品牌大瓶牛奶买了多少瓶?
【答案】任务一:见解析;
任务二:小文购买了大瓶牛奶和小瓶牛奶各3瓶、5瓶;
任务三:小明A品牌大瓶牛奶买了6瓶.
【分析】任务一:设A品牌牛奶大瓶x瓶,则A品牌牛奶小瓶(8﹣x)瓶,根据一共花费89元建立方程求出x的值,看是否为正整数即可得到答案;
任务二:设A品牌牛奶大瓶m瓶,则A品牌牛奶小瓶(8﹣m)瓶,则原价购买的大瓶(m﹣1)瓶,根据一共花费89元建立方程,求出m的值即可得到答案;
任务三:设小明A品牌大瓶牛奶买了t瓶,小瓶买了n瓶,则B品牌牛奶一共有(3t﹣t﹣n)瓶,需要购买B品牌牛奶(3t﹣t﹣n)瓶,根据一共花费210元建立方程求解即可.
【解答】解:任务一:设A品牌牛奶大瓶x瓶,则A品牌牛奶小瓶(8﹣x)瓶,
由题意得,15x+10(8﹣x)=89,
解得,
∵x要为正整数,
∴此时不符合题意,
∴按原价购买,不可能是89元.
任务二:设A品牌牛奶大瓶m瓶,则A品牌牛奶小瓶(8﹣m)瓶,
由题意得,15(m﹣1)+15×0.6+10(8﹣m)=89,
解得m=3,
∴8﹣m=5,
∴小文购买了大瓶牛奶和小瓶牛奶各3瓶、5瓶;
任务三:设小明A品牌牛奶大瓶买了t瓶,小瓶买了n瓶,则B品牌牛奶一共有(3t﹣t﹣n)瓶,
∴需要购买B品牌牛奶(3t﹣t﹣n)瓶,
由题意得,15t+10n+15(3t﹣t﹣n)=210,
解得t=6,
∴小明A品牌大瓶牛奶买了6瓶.
【点评】本题主要考查了一元一次方程的实际应用,正确理解题意列出方程是解题的关键.
7.根据以下素材,探索完成任务.
如何设计板材裁切方案?
素材1 图1中是一张学生椅,主要由靠背、座垫及铁架组成.经测量,该款学生椅的靠背尺寸为40cm×15cm,座垫尺寸为40cm×35cm.图2是靠背与座垫的尺寸示意图.
素材2 因学校需要,某工厂配合制作该款式学生椅.经清点库存时发现,工厂仓库已有大量的学生椅铁架,只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为240cm,宽为40cm. (裁切时不计损耗)
我是板材裁切师
任务一 拟定裁切方案 若要不造成板材浪费,请你设计出一张该板材的所有裁切方法. 方法一:裁切靠背16张和坐垫0张. 方法二:裁切靠背 9 张和坐垫 3 张. 方法三:裁切靠背 6 张和坐垫 2 张.
任务二 确定搭配数量 若该工厂购进50张该型号板材,能制作成多少张学生椅?
任务三 解决实际问题 现需要制作700张学生椅,该工厂仓库现有1张座垫和11张靠背,还需要购买该型号板材多少张(恰好全部用完)?并给出一种裁切方案.
【答案】见试题解答内容
【分析】任务一:设一张该板材裁切靠背m张,坐垫n张,可得:15m+35n=240,求出非负整数解即可;
任务二:列式计算得能制作成240张学生椅;
任务三:设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张,可得:,解方程组可得答案.
【解答】解:任务一:
设一张该板材裁切靠背m张,坐垫n张,
根据题意得:15m+35n=240,
∴n,
∵m,n为非负整数,
∴或或,
∴方法二:裁切靠背9张和坐垫3张;
方法三:裁切靠背2张和坐垫6张;
故答案为:9,3;2,6;
任务二:
∵240(张),
∴该工厂购进50张该型号板材,能制作成240张学生椅;
任务三:
设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张,
根据题意得:,
解得:,
∵57+88=145(张),
∴需要购买该型号板材145张,用其中57张板材裁切靠背9张和坐垫3张,用88张板材裁切靠背2张和坐垫6张.
【点评】本题考查二元一次方程(组)的应用,解题的关键是读懂题意,列出二元一次方程和二元一次方程组.
8.解方程组:.
【答案】见试题解答内容
【分析】利用加减消元法求解即可.
【解答】解:①×2+②得:5x=25,
解得:x=5,
将x=5代入①得:5﹣2y=1,
解得:y=2,
所以原方程组的解是.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
9.小明乘家门口的公共汽车赶往火车站,如果乘公共汽车一直到火车站,到火车站时火车正好开出.于是在公共汽车行驶了一半路程时,小明马上下车,并立即乘出租车前往火车站.出租车的速度是公共汽车速度的2倍,结果在火车开车前15min到达火车站.已知公共汽车的平均速度30km/h,那么小明家到火车站的路程是多少千米?
【答案】30.
【分析】根据公交汽车的平均速度为30km/h,出租车的速度应为60km/h,可设小明家距火车站距离为x km,公共汽车行驶的路程时间应为小时,剩下的的路程,出租车需要时间为:;然后利用在火车开车前15min到达火车站列出方程,解方程求出x的值即可.
【解答】解:设小明家到火车站的路程是x km,由题意,得
.
解得x=30.
答:小明家到火车站的路程是30km.
【点评】本题考查了一元一次方程的应用,根据路程=速度×时间,列出关于x的一元一次方程是解题的关键.
10.某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召,积极扩大粮食生产规模,计划用基地的甲、乙两区农田进行油菜试种,甲区的农田比乙区的农田多10000亩,甲区农田的80%和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同.
(1)求甲、乙两区各有农田多少亩?
(2)在甲、乙两区适宜试种的农田全部种上油菜后,为加强油菜的虫害治理,基地派出一批性能相同的无人机,对试种农田喷洒除虫药,由于两区地势差别,派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),喷洒任务完成后,发现派往甲区的每架次无人机比乙区的平均多喷洒亩,求派往甲区每架次无人机平均喷洒多少亩?
【答案】见试题解答内容
【分析】(1)设乙区有农田x亩,则甲区有农田(x+10000)亩,根据“甲区农田的80%和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同”,可得出关于x的一元一次方程,解之可得出乙区的农田亩数,再将其代入(x+10000)中,即可求出甲区的农田亩数;
(2)设派往甲区每架次无人机平均喷洒y亩,则派往乙区每架次无人机平均喷洒(y)亩,根据派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),可得出关于y的分式方程,解之经检验后,即可得出结论.
【解答】解:(1)设乙区有农田x亩,则甲区有农田(x+10000)亩,
根据题意得:80%(x+10000)=x,
解得:x=40000,
∴x+10000=40000+10000=50000.
答:甲区有农田50000亩,乙区有农田40000亩;
(2)设派往甲区每架次无人机平均喷洒y亩,则派往乙区每架次无人机平均喷洒(y)亩,
根据题意得:1.2,
解得:y=100,
经检验,y=100是所列分式方程的解,且符合题意.
答:派往甲区每架次无人机平均喷洒100亩.
【点评】本题考查了一元一次方程的应用以及分式方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)找准等量关系,正确列出分式方程.
第1页(共1页)
一、选择题
1.关于x的一元一次方程2x+m=6的解为x=1,则m的值为( )
A.3 B.4 C.5 D.6
2.某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.设购买A,B两种劳动工具的件数分别为x,y,那么下面列出的方程组中正确的是( )
A.
B.
C.
D.
3.《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完.问:城中有多少户人家?( )
A.55 B.65 C.75 D.85
二、填空题
4.已知是方程ax+by=3的解,则代数式2a+4b+5的值为 .
三、解答题
5.体育与健康是学校素质教育的重要组成部分,为活跃校园氛围,培养学生团队合作的精神,某校计划开展七年级趣味运动会.
【基础设问】
(1)七年级一班计划购买甲、乙两种型号的羽毛球拍共30副,已知甲种型号的羽毛球拍每副50元,乙种型号的羽毛球拍每副40元,若购买甲、乙两种型号的羽毛球拍共花费1360元,求甲、乙两种型号的羽毛球拍各买了多少副.
(2)王老师组织七年级二班的学生打扫操场,其中男生25人,女生23人,如果让男生单独打扫,需要5h,如果让女生单独打扫,需要7.5h.如果让男生、女生一起打扫1h,再由男生单独完成剩余的部分,求男生共打扫了多长时间.
【能力设问】
(3)东东和乐乐在操场练习跑步,环形跑道周长为400m,乐乐的速度为6m/s,东东的速度为4m/s.
①若他俩同时同地背向跑,则多少秒后两人第一次相遇?
②若他俩同时同向跑,乐乐在东东前面20m,则多少秒后两人第一次相遇?
(4)趣味运动会表演需要使用一种圆柱形小鼓,在劳动课上杨老师带领七年级五班50名学生进行制作,该班男生人数比女生人数少6人,并且每名学生每小时可制作2个鼓身或剪6个鼓面.求男生和女生各有多少人.
追问1:老师组织全班学生制作小鼓,要求一个鼓身配两个鼓面,为了使每小时制作的鼓身与剪出的鼓面刚好配套,应该分配多少名学生制作鼓身?多少名学生剪鼓面?
追问2:若想1小时制作90个小鼓,且制作的鼓身与剪出的鼓面刚好配套,应再加入多少名学生?
【拓展设问】
(5)在足球趣味赛中,共赛了17轮(即每队均需参赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.
①在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
②在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种.
6.双十一期间,大润发超市各个区域都有促销活动,小文一家去逛该超市,准备购买牛奶,根据以下素材,探索完成任务.
生活中的数学问题
素材1 超市有A品牌牛奶大瓶和小瓶两种型号,大瓶牛奶每瓶15元,小瓶牛奶每瓶10元.
素材2 小文去超市购买了8瓶A品牌牛奶,共花了89元.
素材3 过了几天,小明去超市,发现原价每瓶15元的B品牌牛奶“买二送一”促销.
买 2 送 1B品牌牛奶促销套装温馨提醒: 1.买两瓶送一瓶,同款B品牌牛奶; 2.套装不可拆开单卖.
问题解决
任务1 小文妈妈说:按原价购买,不可能是89元!请说明小文妈妈这样说的理由.
任务2 小文看了一下购物小票,发现有1瓶是“会员打6折限购1瓶”的大瓶牛奶,请问小文购买了大瓶牛奶和小瓶牛奶各多少瓶?
任务3 小明按原价购买A品牌大、小瓶牛奶若干瓶,同时购买B品牌促销套装若干套,一共花费210元.其中A品牌大瓶牛奶占所有牛奶瓶数(包括促销套装中赠送牛奶)的.求小明A品牌大瓶牛奶买了多少瓶?
7.根据以下素材,探索完成任务.
如何设计板材裁切方案?
素材1 图1中是一张学生椅,主要由靠背、座垫及铁架组成.经测量,该款学生椅的靠背尺寸为40cm×15cm,座垫尺寸为40cm×35cm.图2是靠背与座垫的尺寸示意图.
素材2 因学校需要,某工厂配合制作该款式学生椅.经清点库存时发现,工厂仓库已有大量的学生椅铁架,只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为240cm,宽为40cm. (裁切时不计损耗)
我是板材裁切师
任务一 拟定裁切方案 若要不造成板材浪费,请你设计出一张该板材的所有裁切方法. 方法一:裁切靠背16张和坐垫0张. 方法二:裁切靠背 张和坐垫 张. 方法三:裁切靠背 张和坐垫 张.
任务二 确定搭配数量 若该工厂购进50张该型号板材,能制作成多少张学生椅?
任务三 解决实际问题 现需要制作700张学生椅,该工厂仓库现有1张座垫和11张靠背,还需要购买该型号板材多少张(恰好全部用完)?并给出一种裁切方案.
8.解方程组:.
9.小明乘家门口的公共汽车赶往火车站,如果乘公共汽车一直到火车站,到火车站时火车正好开出.于是在公共汽车行驶了一半路程时,小明马上下车,并立即乘出租车前往火车站.出租车的速度是公共汽车速度的2倍,结果在火车开车前15min到达火车站.已知公共汽车的平均速度30km/h,那么小明家到火车站的路程是多少千米?
10.某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召,积极扩大粮食生产规模,计划用基地的甲、乙两区农田进行油菜试种,甲区的农田比乙区的农田多10000亩,甲区农田的80%和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同.
(1)求甲、乙两区各有农田多少亩?
(2)在甲、乙两区适宜试种的农田全部种上油菜后,为加强油菜的虫害治理,基地派出一批性能相同的无人机,对试种农田喷洒除虫药,由于两区地势差别,派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),喷洒任务完成后,发现派往甲区的每架次无人机比乙区的平均多喷洒亩,求派往甲区每架次无人机平均喷洒多少亩?
第3章 一次方程(组)
参考答案与试题解析
一、选择题
1.关于x的一元一次方程2x+m=6的解为x=1,则m的值为( )
A.3 B.4 C.5 D.6
【答案】B
【分析】将x=1代入方程2x+m=6,得到关于m的一元一次方程,解方程即可求出m的值.
【解答】解:∵关于x的一元一次方程2x+m=6的解为x=1,
∴2+m=6,
解得m=4.
故选:B.
【点评】本题考查了一元一次方程的解的定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.
2.某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.设购买A,B两种劳动工具的件数分别为x,y,那么下面列出的方程组中正确的是( )
A.
B.
C.
D.
【答案】A
【分析】利用总价=单价×数量,结合学校用1580元购进A,B两种劳动工具共145件,可列出关于x,y的二元一次方程组,此题得解.
【解答】解:∵购进A,B两种劳动工具共145件,
∴x+y=145;
∵A,B两种劳动工具每件分别为10元,12元.且购买这批劳动工具共花费1580元,
∴10x+12y=1580,
∴根据题意可列出方程组.
故选:A.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
3.《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完.问:城中有多少户人家?( )
A.55 B.65 C.75 D.85
【答案】C
【分析】设城中有x户人家,根据“今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完”,即可得出关于x的一元一次方程,解之即可得出结论.
【解答】解:设城中有x户人家,
依题意,得:xx=100,
解得:x=75.
故选:C.
【点评】本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.
二、填空题
4.已知是方程ax+by=3的解,则代数式2a+4b+5的值为 11 .
【答案】11.
【分析】把x与y的值代入方程计算得到a+2b的值,原式变形后代入计算即可求出值.
【解答】解:把代入ax+by=3得:a+2b=3,
则原式=2(a+2b)+5
=2×3+5
=6+5
=11.
故答案为:11.
【点评】此题考查了二元一次方程的解,以及代数式求值,方程的解即为能使方程左右两边相等的未知数的值.
三、解答题
5.体育与健康是学校素质教育的重要组成部分,为活跃校园氛围,培养学生团队合作的精神,某校计划开展七年级趣味运动会.
【基础设问】
(1)七年级一班计划购买甲、乙两种型号的羽毛球拍共30副,已知甲种型号的羽毛球拍每副50元,乙种型号的羽毛球拍每副40元,若购买甲、乙两种型号的羽毛球拍共花费1360元,求甲、乙两种型号的羽毛球拍各买了多少副.
(2)王老师组织七年级二班的学生打扫操场,其中男生25人,女生23人,如果让男生单独打扫,需要5h,如果让女生单独打扫,需要7.5h.如果让男生、女生一起打扫1h,再由男生单独完成剩余的部分,求男生共打扫了多长时间.
【能力设问】
(3)东东和乐乐在操场练习跑步,环形跑道周长为400m,乐乐的速度为6m/s,东东的速度为4m/s.
①若他俩同时同地背向跑,则多少秒后两人第一次相遇?
②若他俩同时同向跑,乐乐在东东前面20m,则多少秒后两人第一次相遇?
(4)趣味运动会表演需要使用一种圆柱形小鼓,在劳动课上杨老师带领七年级五班50名学生进行制作,该班男生人数比女生人数少6人,并且每名学生每小时可制作2个鼓身或剪6个鼓面.求男生和女生各有多少人.
追问1:老师组织全班学生制作小鼓,要求一个鼓身配两个鼓面,为了使每小时制作的鼓身与剪出的鼓面刚好配套,应该分配多少名学生制作鼓身?多少名学生剪鼓面?
追问2:若想1小时制作90个小鼓,且制作的鼓身与剪出的鼓面刚好配套,应再加入多少名学生?
【拓展设问】
(5)在足球趣味赛中,共赛了17轮(即每队均需参赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.
①在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
②在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种.
【答案】(1)甲种型号羽毛球拍买了16副,乙种型号的羽毛球拍买了14副;
(2)小时;
(3)①40秒;
②190秒;
(4)男生有22人,女生有28人;
追问1.应分配30名学生制作鼓身,则20名学生剪鼓面;
追问2.应再加入25名学生;
(5)①3场;
②小虎足球队踢负场数的情况有3种,分别是1,5,7场.
【分析】(1)设甲种型号羽毛球拍买了z副,则乙种型号的羽毛球拍买了(30﹣z)副,由题意得出方程50z+40(30﹣z)=1360,根据解一元一次方程的方法求出z的值,进而得出答案;
(2)设男生共打扫了w小时,由题意列出方程:,根据解一元一次方程的方法求解即可;
(3)①设t秒后两人第一次相遇,由题意列出方程:6t+4t=400,根据解一元一次方程的方法求解即可;
②设b秒后两人第一次相遇,根据题意列出方程:6b+20﹣4b=400,根据解一元一次方程的方法求解即可.
(4)设男生有x人,女生有(50﹣x)人,根据题意列出方程:x+6=50﹣x,根据解一元一次方程的方法求出x的值,进而得出答案;
追问1.设分配a名学生制作鼓身,则(50﹣a)名学生剪鼓面,由题意可列出方程:2×2a=6(50﹣a),根据解一元一次方程的方法求出a的值,进而得出答案;
追问2.根据追问1可知,50名学生1小时可制作60个小鼓,则若要每小时制作90个小鼓,需要增加一半的人数.
(5)①设小虎队胜了x场,平了y场,则负了y场,由题意列出方程组:,根据解二元一次方程组的方法求解即可;
②设小虎队胜了m场,负了n场,踢平场数是踢负场数的k倍(k为整数),由题意列出方程组:,得出,由n为正整数,进而得出答案.
【解答】解:(1)设甲种型号羽毛球拍买了z副,则乙种型号的羽毛球拍买了(30﹣z)副,
由题意,得50z+40(30﹣z)=1360,
解得:z=16,
∴30﹣z=30﹣16=14.
答:甲种型号羽毛球拍买了16副,乙种型号的羽毛球拍买了14副.
(2)设男生共打扫了w小时,
由题意,得,
解得:.
答:男生共打扫了小时.
(3)①设t秒后两人第一次相遇,
由题意,得6t+4t=400,
解得:t=40.
答:40秒后两人第一次相遇;
②设b秒后两人第一次相遇,
由题意,得6b+20﹣4b=400,
解得:b=190.
答:190秒后两人第一次相遇.
(4)设男生有x人,女生有(50﹣x)人,
由题意,得x+6=50﹣x,
解得:x=22,
∴50﹣x=50﹣22=28.
答:男生有22人,女生有28人.
追问1.设分配a名学生制作鼓身,则(50﹣a)名学生剪鼓面,
由题意,得2×2a=6(50﹣a),
解得:a=30,
∴50﹣a=50﹣30=20.
答:应分配30名学生制作鼓身,则20名学生剪鼓面;
追问2.由追问1可知,分配30名学生制作鼓身,20名学生剪鼓面,
则1小时可制作小鼓30×2=60(个),还需制作90﹣60=30(个)小鼓,
∴50÷2=25(人).
答:应再加入25名学生.
(5)①设小虎队胜了x场,平了y场,则负了y场,
由题意,得,
解得:.
答:该队胜了3场.
②设小虎队胜了m场,负了n场,踢平场数是踢负场数的k倍(k为整数),
由题意,得,
解得:,
又∵n为正整数,
∴,,.
答:小虎足球队踢负场数的情况有3种,分别是1,5,7场.
【点评】本题考查了一元一次方程的应用,二元一次方程组的应用,根据题意,找准等量关系,正确列出方程,方程组是解题的关键.
6.双十一期间,大润发超市各个区域都有促销活动,小文一家去逛该超市,准备购买牛奶,根据以下素材,探索完成任务.
生活中的数学问题
素材1 超市有A品牌牛奶大瓶和小瓶两种型号,大瓶牛奶每瓶15元,小瓶牛奶每瓶10元.
素材2 小文去超市购买了8瓶A品牌牛奶,共花了89元.
素材3 过了几天,小明去超市,发现原价每瓶15元的B品牌牛奶“买二送一”促销.
B品牌牛奶促销套装温馨提醒: 1.买两瓶送一瓶,同款B品牌牛奶; 2.套装不可拆开单卖.
问题解决
任务1 小文妈妈说:按原价购买,不可能是89元!请说明小文妈妈这样说的理由.
任务2 小文看了一下购物小票,发现有1瓶是“会员打6折限购1瓶”的大瓶牛奶,请问小文购买了大瓶牛奶和小瓶牛奶各多少瓶?
任务3 小明按原价购买A品牌大、小瓶牛奶若干瓶,同时购买B品牌促销套装若干套,一共花费210元.其中A品牌大瓶牛奶占所有牛奶瓶数(包括促销套装中赠送牛奶)的.求小明A品牌大瓶牛奶买了多少瓶?
【答案】任务一:见解析;
任务二:小文购买了大瓶牛奶和小瓶牛奶各3瓶、5瓶;
任务三:小明A品牌大瓶牛奶买了6瓶.
【分析】任务一:设A品牌牛奶大瓶x瓶,则A品牌牛奶小瓶(8﹣x)瓶,根据一共花费89元建立方程求出x的值,看是否为正整数即可得到答案;
任务二:设A品牌牛奶大瓶m瓶,则A品牌牛奶小瓶(8﹣m)瓶,则原价购买的大瓶(m﹣1)瓶,根据一共花费89元建立方程,求出m的值即可得到答案;
任务三:设小明A品牌大瓶牛奶买了t瓶,小瓶买了n瓶,则B品牌牛奶一共有(3t﹣t﹣n)瓶,需要购买B品牌牛奶(3t﹣t﹣n)瓶,根据一共花费210元建立方程求解即可.
【解答】解:任务一:设A品牌牛奶大瓶x瓶,则A品牌牛奶小瓶(8﹣x)瓶,
由题意得,15x+10(8﹣x)=89,
解得,
∵x要为正整数,
∴此时不符合题意,
∴按原价购买,不可能是89元.
任务二:设A品牌牛奶大瓶m瓶,则A品牌牛奶小瓶(8﹣m)瓶,
由题意得,15(m﹣1)+15×0.6+10(8﹣m)=89,
解得m=3,
∴8﹣m=5,
∴小文购买了大瓶牛奶和小瓶牛奶各3瓶、5瓶;
任务三:设小明A品牌牛奶大瓶买了t瓶,小瓶买了n瓶,则B品牌牛奶一共有(3t﹣t﹣n)瓶,
∴需要购买B品牌牛奶(3t﹣t﹣n)瓶,
由题意得,15t+10n+15(3t﹣t﹣n)=210,
解得t=6,
∴小明A品牌大瓶牛奶买了6瓶.
【点评】本题主要考查了一元一次方程的实际应用,正确理解题意列出方程是解题的关键.
7.根据以下素材,探索完成任务.
如何设计板材裁切方案?
素材1 图1中是一张学生椅,主要由靠背、座垫及铁架组成.经测量,该款学生椅的靠背尺寸为40cm×15cm,座垫尺寸为40cm×35cm.图2是靠背与座垫的尺寸示意图.
素材2 因学校需要,某工厂配合制作该款式学生椅.经清点库存时发现,工厂仓库已有大量的学生椅铁架,只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为240cm,宽为40cm. (裁切时不计损耗)
我是板材裁切师
任务一 拟定裁切方案 若要不造成板材浪费,请你设计出一张该板材的所有裁切方法. 方法一:裁切靠背16张和坐垫0张. 方法二:裁切靠背 9 张和坐垫 3 张. 方法三:裁切靠背 6 张和坐垫 2 张.
任务二 确定搭配数量 若该工厂购进50张该型号板材,能制作成多少张学生椅?
任务三 解决实际问题 现需要制作700张学生椅,该工厂仓库现有1张座垫和11张靠背,还需要购买该型号板材多少张(恰好全部用完)?并给出一种裁切方案.
【答案】见试题解答内容
【分析】任务一:设一张该板材裁切靠背m张,坐垫n张,可得:15m+35n=240,求出非负整数解即可;
任务二:列式计算得能制作成240张学生椅;
任务三:设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张,可得:,解方程组可得答案.
【解答】解:任务一:
设一张该板材裁切靠背m张,坐垫n张,
根据题意得:15m+35n=240,
∴n,
∵m,n为非负整数,
∴或或,
∴方法二:裁切靠背9张和坐垫3张;
方法三:裁切靠背2张和坐垫6张;
故答案为:9,3;2,6;
任务二:
∵240(张),
∴该工厂购进50张该型号板材,能制作成240张学生椅;
任务三:
设用x张板材裁切靠背9张和坐垫3张,用y张板材裁切靠背2张和坐垫6张,
根据题意得:,
解得:,
∵57+88=145(张),
∴需要购买该型号板材145张,用其中57张板材裁切靠背9张和坐垫3张,用88张板材裁切靠背2张和坐垫6张.
【点评】本题考查二元一次方程(组)的应用,解题的关键是读懂题意,列出二元一次方程和二元一次方程组.
8.解方程组:.
【答案】见试题解答内容
【分析】利用加减消元法求解即可.
【解答】解:①×2+②得:5x=25,
解得:x=5,
将x=5代入①得:5﹣2y=1,
解得:y=2,
所以原方程组的解是.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
9.小明乘家门口的公共汽车赶往火车站,如果乘公共汽车一直到火车站,到火车站时火车正好开出.于是在公共汽车行驶了一半路程时,小明马上下车,并立即乘出租车前往火车站.出租车的速度是公共汽车速度的2倍,结果在火车开车前15min到达火车站.已知公共汽车的平均速度30km/h,那么小明家到火车站的路程是多少千米?
【答案】30.
【分析】根据公交汽车的平均速度为30km/h,出租车的速度应为60km/h,可设小明家距火车站距离为x km,公共汽车行驶的路程时间应为小时,剩下的的路程,出租车需要时间为:;然后利用在火车开车前15min到达火车站列出方程,解方程求出x的值即可.
【解答】解:设小明家到火车站的路程是x km,由题意,得
.
解得x=30.
答:小明家到火车站的路程是30km.
【点评】本题考查了一元一次方程的应用,根据路程=速度×时间,列出关于x的一元一次方程是解题的关键.
10.某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召,积极扩大粮食生产规模,计划用基地的甲、乙两区农田进行油菜试种,甲区的农田比乙区的农田多10000亩,甲区农田的80%和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同.
(1)求甲、乙两区各有农田多少亩?
(2)在甲、乙两区适宜试种的农田全部种上油菜后,为加强油菜的虫害治理,基地派出一批性能相同的无人机,对试种农田喷洒除虫药,由于两区地势差别,派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),喷洒任务完成后,发现派往甲区的每架次无人机比乙区的平均多喷洒亩,求派往甲区每架次无人机平均喷洒多少亩?
【答案】见试题解答内容
【分析】(1)设乙区有农田x亩,则甲区有农田(x+10000)亩,根据“甲区农田的80%和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同”,可得出关于x的一元一次方程,解之可得出乙区的农田亩数,再将其代入(x+10000)中,即可求出甲区的农田亩数;
(2)设派往甲区每架次无人机平均喷洒y亩,则派往乙区每架次无人机平均喷洒(y)亩,根据派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),可得出关于y的分式方程,解之经检验后,即可得出结论.
【解答】解:(1)设乙区有农田x亩,则甲区有农田(x+10000)亩,
根据题意得:80%(x+10000)=x,
解得:x=40000,
∴x+10000=40000+10000=50000.
答:甲区有农田50000亩,乙区有农田40000亩;
(2)设派往甲区每架次无人机平均喷洒y亩,则派往乙区每架次无人机平均喷洒(y)亩,
根据题意得:1.2,
解得:y=100,
经检验,y=100是所列分式方程的解,且符合题意.
答:派往甲区每架次无人机平均喷洒100亩.
【点评】本题考查了一元一次方程的应用以及分式方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)找准等量关系,正确列出分式方程.
第1页(共1页)
同课章节目录
