2025年新八年级数学人教版暑假大讲堂第八讲 全等三角形及其性质(含解析)
文档属性
| 名称 | 2025年新八年级数学人教版暑假大讲堂第八讲 全等三角形及其性质(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览



文档简介
2025年新八年级数学人教版暑假大讲堂
第八讲 全等三角形及其性质
知识点梳理
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
要点诠释:
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
知识点2 全等三角形
能够完全重合的两个三角形叫全等三角形.
要点诠释:
用符号“≌”表示,如△ABC ≌ △A'B'C',对应顶点字母写在对应位置.
隐含等量元素 :公共边、对顶角、平行线同位角等
知识点3 对应边、对应角和对应顶点
对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
1.在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
2. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
知识点4 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
要点诠释:
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
题型1 图形的全等
例1.嘉嘉、淇淇和笑笑在学习全等三角形时,关于“全等形”提出了三种不同的说法.
嘉嘉说:形状、大小相同的图形是全等形.
淇淇说:能够完全重合的图形是全等形.
笑笑说:各边都相等的图形是全等形.
他们的说法中,正确的有( )
A.0个 B.1个 C.2个 D.3个
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
针对训练1
1.下列各组图形全等的是( )
A. B.
C. D.
2.下列选项中能够表示两个全等图形的是( )
A.形状相同的两个图形 B.能够完全重合的两个图形
C.面积相等的两个图形 D.周长相等的两个图形
3.下列图形中,是全等图形的是( )
A.a,b,c,d B.a与b C.b,c,d D.a与c
4.下列汽车标志中,是由多个全等图形组成的有( )个
A.1 B.2 C.3 D.4
题型2 将已知图形分割成几个全等图形
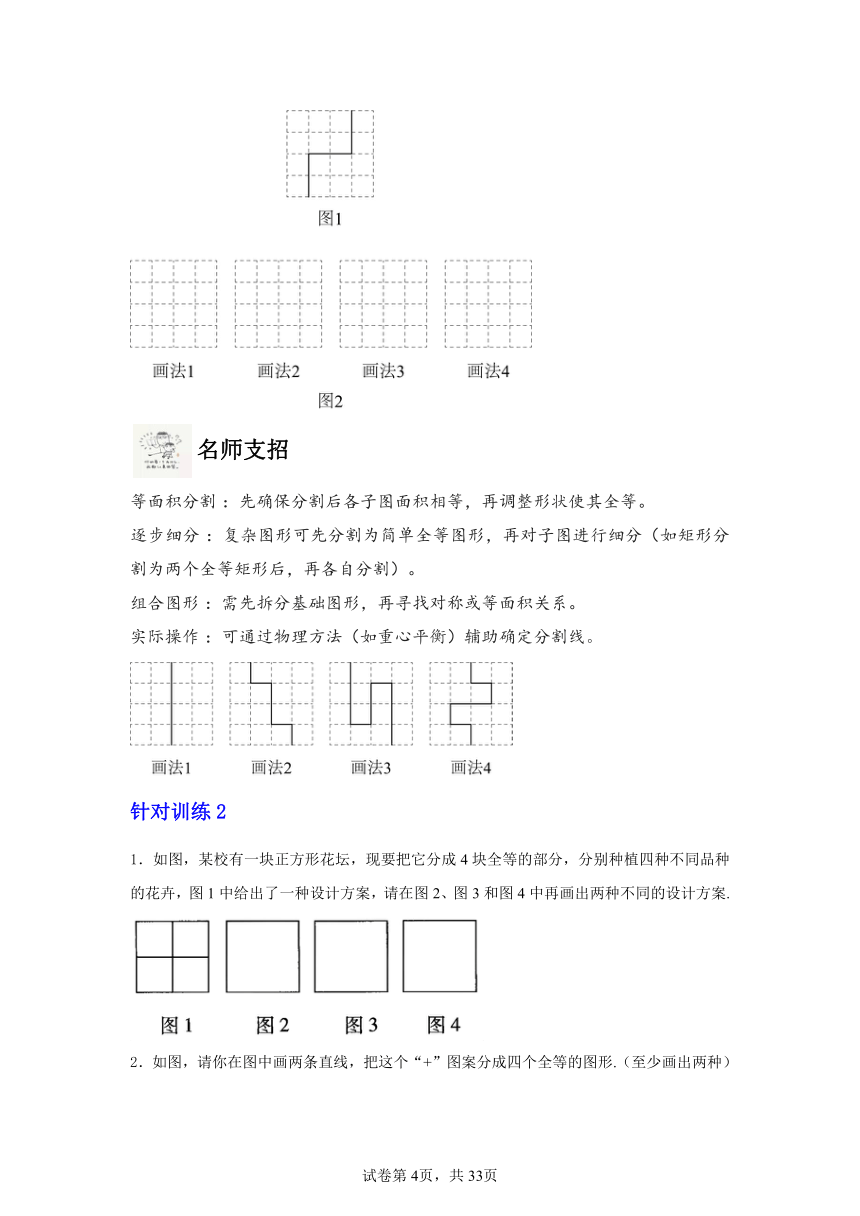
例2.如图1,把大小为的正方形网格分割成了两个全等形.请在图2中,沿着虚线画出四种不同的分割方法,把的正方形网格分割成两个全等形.
等面积分割 :先确保分割后各子图面积相等,再调整形状使其全等。
逐步细分 :复杂图形可先分割为简单全等图形,再对子图进行细分(如矩形分割为两个全等矩形后,再各自分割)。
组合图形 :需先拆分基础图形,再寻找对称或等面积关系。
实际操作 :可通过物理方法(如重心平衡)辅助确定分割线。
针对训练2
1.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图1中给出了一种设计方案,请在图2、图3和图4中再画出两种不同的设计方案.
2.如图,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(至少画出两种)
3.沿图中的虚线画线,把下面的图形划分为两个全等的图形(用二种不同方法):
4.如图,将图形分成大小、形状相同的三块,并且每块带一个☆.
题型3 全等三角形对应元素
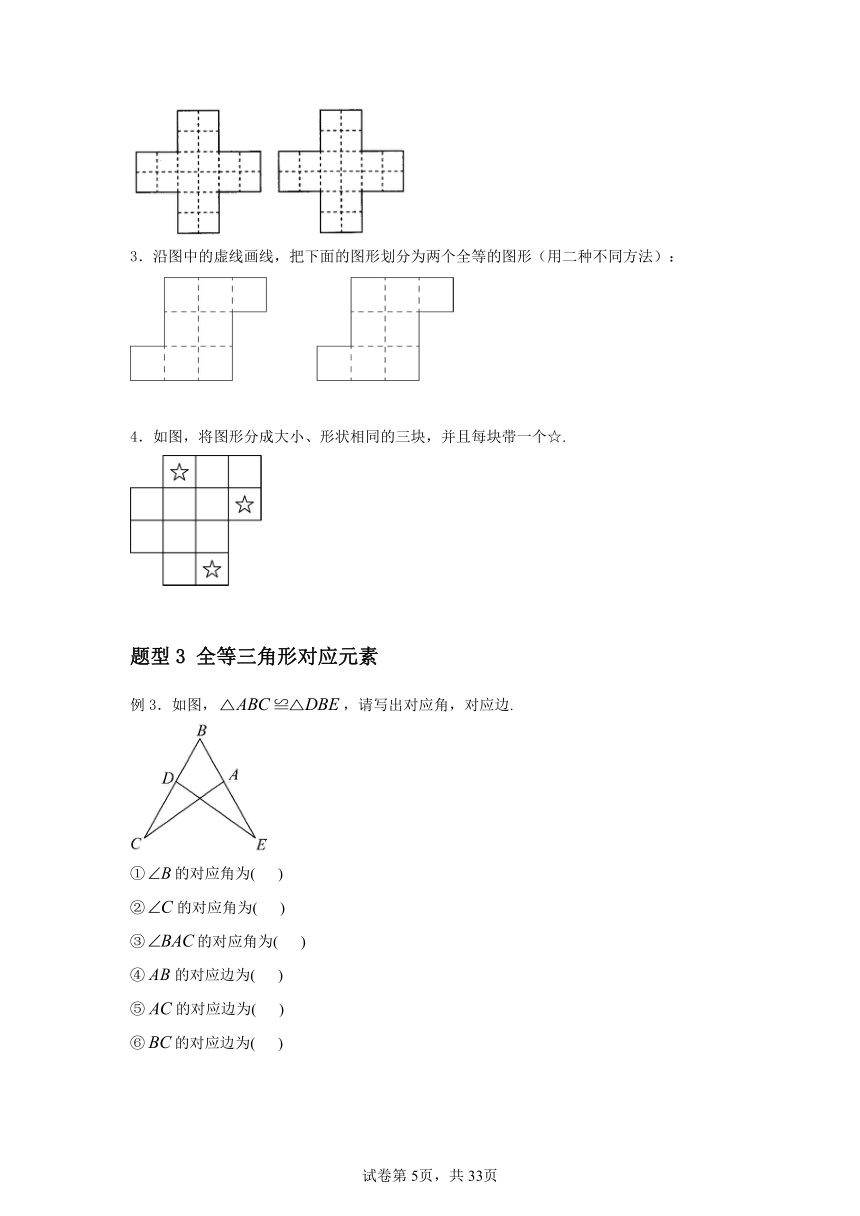
例3.如图,,请写出对应角,对应边.
①的对应角为( )
②的对应角为( )
③的对应角为( )
④的对应边为( )
⑤的对应边为( )
⑥的对应边为( )
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
针对训练3
1.如图,,下列结论:①与是对应边;②与是对应边;③与是对应角;④与是对应角.其中正确的有( )
A.①③ B.②③ C.①④ D.②④
2.如图所示,,C,D是对应点,下列结论错误的是( )
A.与是对应角 B.与是对应角
C.与是对应边 D.与是对应边
3.如图,,和是对应角,AB和AC是对应边.写出其他对应边及对应角.
.
4.如图,,和CD,BC和DA是对应边.写出其他对应边及对应角.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
.
题型4 全等三角形的性质
例4.如图,,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
针对训练4
1.如图,已知,若,,则的长为( )
A.6 B.8 C.10 D.12
2.已知图中的两个三角形全等,则等于( )
A. B. C. D.
3.如图,,点E在AB上,AC与BD交于点F,,,,.
(1)求AE的长度;
(2)求的度数.
4.如图,已知,点E在上,与相交于点F.
(1)若,,求线段的长;
(2)已知,,求的度数.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
.
易错易混诠释
1.在图形中不能区分对应边和对应角,
复合变换(如平移、旋转、对称)后的图形,需准确标记对应点及边。
针对训练1
1.如图,,点和是对应点,点和是对应点,则的对应角是( )
A. B. C. D.
2.如图,,和,和是对应边,则的对应角是( )
A. B. C. D.
2.格式规范问题:书写顺序错误
针对训练2
1.若,则的对应边是 .
3.周长相等条件误用错误套用等式性质
针对训练3
1.如图,,若,,,则的周长等于 .
2.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.若两个图形周长相等,则它们一定是全等图形
C.两个等边三角形一定是全等图形
D.能够完全重合的两个图形是全等图形
创新拓展能力提升
1.将下图分成四个全等的图形,而且每一份图形中恰好有“巧分图形”四个字.
2.(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
①写出图中一对全等的三角形,并写出它们的所有对应角;
②设的度数为x,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.
3.如图,长方形中,cm,cm,现有一动点P从A出发以2cm/秒的速度,沿长方形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒.
(1)当秒时, cm;
(2)Q为边上的点,且,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与全等.
4.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.
(1)求证:∠ACD=∠B;
(2)若∠A=40°,求∠BCD的度数.
2025年新八年级数学人教版暑假大讲堂
第九讲 全等三角形及其性质
知识点梳理
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
要点诠释:
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
知识点2 全等三角形
能够完全重合的两个三角形叫全等三角形.
要点诠释:
用符号“≌”表示,如△ABC ≌ △A'B'C',对应顶点字母写在对应位置.
隐含等量元素 :公共边、对顶角、平行线同位角等
知识点3 对应边、对应角和对应顶点
对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
1.在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
2. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
知识点4 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
要点诠释:
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
题型1 图形的全等
例1.嘉嘉、淇淇和笑笑在学习全等三角形时,关于“全等形”提出了三种不同的说法.
嘉嘉说:形状、大小相同的图形是全等形.
淇淇说:能够完全重合的图形是全等形.
笑笑说:各边都相等的图形是全等形.
他们的说法中,正确的有( )
A.0个 B.1个 C.2个 D.3个
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
答案:C
解析:嘉嘉说:形状、大小相同的图形是全等形,正确,符合题意.
淇淇说:能够完全重合的图形是全等形,正确,符合题意.
笑笑说:各边都相等的图形是全等形,不一定正确,因为相等两边的夹角不一定相等,不符合题意.
故选:C.
针对训练1
1.下列各组图形全等的是( )
A. B.
C. D.
答案:C
解析:能够完全重合的两个平面图形,叫全等图形,故A、B、D都不符合题意。
故选C
2.下列选项中能够表示两个全等图形的是( )
A.形状相同的两个图形 B.能够完全重合的两个图形
C.面积相等的两个图形 D.周长相等的两个图形
答案:B
解析:A、形状相同的两个图形,大小不一定相同,故此选项错误,不符合题意;
B、能够完全重合的两个图形是全等图形,故此选项正确,符合题意;
C、面积相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
D、周长相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
故选:B.
3.下列图形中,是全等图形的是( )
A.a,b,c,d B.a与b C.b,c,d D.a与c
答案:D
解析:能够完全重合的两个平面图形,叫全等图形.
由图可知,a与c是全等图形.
故选:D.
4.下列汽车标志中,是由多个全等图形组成的有( )个
A.1 B.2 C.3 D.4
答案:C
解析:第一个图形中,三个椭圆不全等,不是全等图形,不符合题意;
第二个图形中,上下两部分图形大小形状相同,是全等图形,符合题意;
第三个图形中,三个菱形大小形状相同,是全等图形,符合题意;
第四个图形中,四个圆形大小形状相同,是全等图形,符合题意;
即是由多个全等图形组成的有3个,
故选:C.
题型2 将已知图形分割成几个全等图形
例2.如图1,把大小为的正方形网格分割成了两个全等形.请在图2中,沿着虚线画出四种不同的分割方法,把的正方形网格分割成两个全等形.
等面积分割 :先确保分割后各子图面积相等,再调整形状使其全等。
逐步细分 :复杂图形可先分割为简单全等图形,再对子图进行细分(如矩形分割为两个全等矩形后,再各自分割)。
组合图形 :需先拆分基础图形,再寻找对称或等面积关系。
实际操作 :可通过物理方法(如重心平衡)辅助确定分割线。
答案:见解析
解析:要求分成全等的两块,
每块图形要包含有8个小正方形.
针对训练2
1.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图1中给出了一种设计方案,请在图2、图3和图4中再画出两种不同的设计方案.
答案:图见解析
解析:方案如下.(答案不唯一,合理即可)
2.如图,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(至少画出两种)
答案:图见解析
解析:如图.(答案不唯一)
3.沿图中的虚线画线,把下面的图形划分为两个全等的图形(用二种不同方法):
答案:见解析
解析:如图所示:
4.如图,将图形分成大小、形状相同的三块,并且每块带一个☆.
答案:见解析
解析:如下图所示,将图形分成大小、形状相同的三块,并且每块带一个☆,
题型3 全等三角形对应元素
例3.如图,,请写出对应角,对应边.
①的对应角为( )
②的对应角为( )
③的对应角为( )
④的对应边为( )
⑤的对应边为( )
⑥的对应边为( )
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
答案:见解析
解析:①的对应角为,
②的对应角为,
③的对应角为,
④的对应边为,
⑤对应边为,
⑥的对应边为.
针对训练3
1.如图,,下列结论:①与是对应边;②与是对应边;③与是对应角;④与是对应角.其中正确的有( )
A.①③ B.②③ C.①④ D.②④
答案:B
解析:由得:
①与是对应边,故①不符合题意;
②与是对应边,故②符合题意;
③与是对应角,故③符合题意;
④与是对应角,与是对应角,故④不符合题意;
故正确的有②③,
故选:B.
2.如图所示,,C,D是对应点,下列结论错误的是( )
A.与是对应角 B.与是对应角
C.与是对应边 D.与是对应边
答案:C
解析:,
,,,
A,B,D选项正确,不符合题意,
故选:C.
3.如图,,和是对应角,AB和AC是对应边.写出其他对应边及对应角.
答案:见解析
解析:对应边:AN与AM,BN与CM.
对应角:与,与.
4.如图,,和CD,BC和DA是对应边.写出其他对应边及对应角.
答案:见解析
解析:对应边:AC与CA.
对应角:与,与,与.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
答案:(1)见解析
(2)
解析:(1)对应边:AE与AD,EC与DB,AC与AB.
对应角:与,与,与.
(2)因为,,
所以.
又因为在中,,,
,,,
所以.
题型4 全等三角形的性质
例4.如图,,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
答案:(1)见解析
(2)35°
解析:(1)证明:,
,
即,
;
(2),,
,
,
,
,,
.
针对训练4
1.如图,已知,若,,则的长为( )
A.6 B.8 C.10 D.12
答案:B
解析:,
,
,
故选:B.
2.已知图中的两个三角形全等,则等于( )
A. B. C. D.
答案:D
解析:由全等三角形的性质得:是边a和c的夹角,
∴,
故选:D.
3.如图,,点E在AB上,AC与BD交于点F,,,,.
(1)求AE的长度;
(2)求的度数.
答案:(1)3
(2)
解析:(1),
,.
(2),
,,
.
4.如图,已知,点E在上,与相交于点F.
(1)若,,求线段的长;
(2)已知,,求的度数.
答案:(1)
(2)
解析:(1)∵,,,
∴,,
∴;
(2)∵,,,
∴,,,
∴,
∴,
∴,
∴.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
答案:(1)见解析
(2)
解析:(1)对应边:AE与AD,EC与DB,AC与AB.
对应角:与,与,与.
(2)因为,,
所以.
又因为在中,,,
,,,
所以.
易错易混诠释
1.在图形中不能区分对应边和对应角,
复合变换(如平移、旋转、对称)后的图形,需准确标记对应点及边。
针对训练1
1.如图,,点和是对应点,点和是对应点,则的对应角是( )
A. B. C. D.
【答案】.B
【分析】本题考查了全等三角形的概念,根据全等三角形的概念即可判断,正确找出对应边,对应角是解题的关键.
【详解】解:∵,点和是对应点,点和是对应点,
∴的对应角是,
故选:.
2.如图,,和,和是对应边,则的对应角是( )
A. B. C. D.
【答案】B
【分析】本题主要考查全等三角形的概念,根据已知条件,和,和是对应边,点与点对应点,点与点是对应点,由此即可得到的对应角,理解其概念是解题的关键.
【详解】∵,
∴∠的对应角是,
故选:.
2.格式规范问题:书写顺序错误
针对训练2
1.若,则的对应边是 .
【答案】/
【分析】本题考查了全等三角形的概念,根据全等三角形的概念判断即可.
【详解】解:∵,
∴的对应边是,
故答案为:.
2.已知A与,B与是对应点,则和全等用符号语言表示为:
【答案】
【分析】本题主要考查了全等三角形的概念,根据全等三角形的概念求解即可.
【详解】解:A与,B与是对应点,则和全等用符号语言表示为,
故答案为:.
3.周长相等条件误用错误套用等式性质
针对训练3
1.如图,,若,,,则的周长等于 .
【答案】13
【分析】本题考查了全等三角形性质的运用,运用全等三角形的性质,找对对应边,即可得三边边长,然后根据三角形的周长公式求解即可.
【详解】解:∵,,
∴,,,
∴的周长为.
故答案为:13.
2.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.若两个图形周长相等,则它们一定是全等图形
C.两个等边三角形一定是全等图形
D.能够完全重合的两个图形是全等图形
【答案】D
【分析】根据全等三角形的定义进行判断作答即可.
【详解】解:两个面积相等的图形,不一定是全等图形,A错误,故不符合要求;
若两个图形周长相等,则它们不一定是全等图形,B错误,故不符合要求;
两个等边三角形不一定是全等图形,C错误,故不符合要求;
能够完全重合的两个图形是全等图形,D正确,故符合要求;
故选:D.
【点睛】本题考查了全等三角形的定义.解题的关键在于对知识的熟练掌握.
创新拓展能力提升
1.将下图分成四个全等的图形,而且每一份图形中恰好有“巧分图形”四个字.
【答案】见解析.
【详解】试题分析:要分成四个全等的图形,且每个图形中恰好有“巧分图形”四个字,所以相同的字必须分开,由此分图即可.
试题解析:图(a)中共有36个小方格,平分成4份后,每份应是9个小方格;因为第一份中要有“巧分图形”四个字,所以相同的两个字必须分支;又因为分成的每一份一定要通过大正方形的中心点,所以正方形中间的四个小方格一定是分开的,其中有一块已有“巧”字,它的下面一格一定是与“图”字相连如图(b)
2.(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
①写出图中一对全等的三角形,并写出它们的所有对应角;
②设的度数为x,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.
【答案】(1)①△EAD≌△EA′D,其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;②∠1=180° 2x,∠2=180° 2y; ③∠A=(∠1+∠2);(2)变化,∠A=(∠2-∠1),见详解
【分析】(1)①根据翻折方法可得△ADE≌△A′DE;
②根据翻折方法可得∠AEA′=2x,∠ADA′=2y,再根据平角定义可得∠1=180°-2x,∠2=180°-2y;
③首先由∠1=180°-2x,2=180°-2y,可得x=90-∠1,y=90-∠2,再根据三角形内角和定理可得∠A=180°-x-y,再利用等量代换可得∠A=(∠1+∠2);
(2)根据折叠的性质和三角形内角和定理解答即可.
【详解】(1)①根据翻折的性质知△EAD≌△EA′D,
其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;
②)∵∠AED=x,∠ADE=y,
∴∠AEA′=2x,∠ADA′=2y,
∴∠1=180°-2x,∠2=180°-2y;
③∠A=(∠1+∠2);
∵∠1=180°-2x,∠2=180°-2y,
∴x=90-∠1,y=90-∠2,
∴∠A=180°-x-y=190-(90-∠1)-(90-∠2)=(∠1+∠2).
(2))∵△A′DE是△ADE沿DE折叠得到,
∴∠A′=∠A,
又∵∠AEA′=180°-∠2,∠3=∠A′+∠1,
∴∠A+∠AEA′+∠3=180°,
即∠A+180°-∠2+∠A′+∠1=180°,
整理得,2∠A=∠2-∠1.
∴∠A=(∠2-∠1).
【点睛】此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
3.如图,长方形中,cm,cm,现有一动点P从A出发以2cm/秒的速度,沿长方形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒.
(1)当秒时, cm;
(2)Q为边上的点,且,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与全等.
【答案】(1)2
(2)2.5或4.5或7.5或9.5
【分析】(1)当秒时,点P运动到线段上,即可得到的长度;
(2)根据题意,要使一个三角形与全等,则点P的位置可以有四个,根据点P运动的位置,即可计算出时间.
【详解】(1)解:当t=3秒时,点P走过的路程为:,
∵,
∴点P运动到线段上,
∴cm,
故答案是:2;
(2)根据题意,如图,连接,则,,,
∴要使一个三角形与全等,则另一条直角边必须等于,
①当点P运动到时,,此时,
∴点P的路程为:,
∴,
②当点P运动到时,,此时,
∴点P的路程为:,
∴,
③当点P运动到时,,此时,
∴点P的路程为:,
∴,
④当点P运动到时,即P与Q重合时,,此时,
∴点P的路程为:,
∴,
综上所述,时间的值可以是:t=2.5s,4.5s,7.5s或9.5s.
【点睛】本题考查了全等三角形的判定与性质,线段的动点问题,等腰三角形的判定,解题的关键是掌握全等三角形的判定与性质及动点的运动状态,从而进行分类讨论.
4.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.
(1)求证:∠ACD=∠B;
(2)若∠A=40°,求∠BCD的度数.
【答案】(1)证明见解析;(2)140°.
【详解】试题分析:(1)根据平行线的性质可得∠ACB=∠DEC,∠ACD=∠D,再由∠ACD=∠B可得∠D=∠B,然后可利用AAS证明△ABC≌△CDE,进而得到CB=DE;
(2)根据全等三角形的性质可得∠A=∠DCE=40°,然后根据邻补角的性质进行计算即可.
试题解析:(1)证明:∵AC∥DE, ∴∠ACB=∠E,∠ACD=∠D,在△ACB和△CDB中,,∴△ABC≌△CDE,∴∠B=∠D,∴∠ACD=∠B
(2)解:∵△ABC≌△CDE, ∴∠A=∠DCE=40°,∴∠BCD=180°﹣∠ECD=140°.
点睛:此题主要考查了全等三角形的性质和判定,关键是掌握全等三角形的性质证明线段和角相等的重要工具.
典例精讲
名师支招
名师支招
名师支招
名师支招
典例精讲
名师支招
变式训练1
名师支招
名师支招
名师支招
试卷第1页,共3页
试卷第1页,共3页
第八讲 全等三角形及其性质
知识点梳理
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
要点诠释:
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
知识点2 全等三角形
能够完全重合的两个三角形叫全等三角形.
要点诠释:
用符号“≌”表示,如△ABC ≌ △A'B'C',对应顶点字母写在对应位置.
隐含等量元素 :公共边、对顶角、平行线同位角等
知识点3 对应边、对应角和对应顶点
对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
1.在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
2. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
知识点4 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
要点诠释:
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
题型1 图形的全等
例1.嘉嘉、淇淇和笑笑在学习全等三角形时,关于“全等形”提出了三种不同的说法.
嘉嘉说:形状、大小相同的图形是全等形.
淇淇说:能够完全重合的图形是全等形.
笑笑说:各边都相等的图形是全等形.
他们的说法中,正确的有( )
A.0个 B.1个 C.2个 D.3个
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
针对训练1
1.下列各组图形全等的是( )
A. B.
C. D.
2.下列选项中能够表示两个全等图形的是( )
A.形状相同的两个图形 B.能够完全重合的两个图形
C.面积相等的两个图形 D.周长相等的两个图形
3.下列图形中,是全等图形的是( )
A.a,b,c,d B.a与b C.b,c,d D.a与c
4.下列汽车标志中,是由多个全等图形组成的有( )个
A.1 B.2 C.3 D.4
题型2 将已知图形分割成几个全等图形
例2.如图1,把大小为的正方形网格分割成了两个全等形.请在图2中,沿着虚线画出四种不同的分割方法,把的正方形网格分割成两个全等形.
等面积分割 :先确保分割后各子图面积相等,再调整形状使其全等。
逐步细分 :复杂图形可先分割为简单全等图形,再对子图进行细分(如矩形分割为两个全等矩形后,再各自分割)。
组合图形 :需先拆分基础图形,再寻找对称或等面积关系。
实际操作 :可通过物理方法(如重心平衡)辅助确定分割线。
针对训练2
1.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图1中给出了一种设计方案,请在图2、图3和图4中再画出两种不同的设计方案.
2.如图,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(至少画出两种)
3.沿图中的虚线画线,把下面的图形划分为两个全等的图形(用二种不同方法):
4.如图,将图形分成大小、形状相同的三块,并且每块带一个☆.
题型3 全等三角形对应元素
例3.如图,,请写出对应角,对应边.
①的对应角为( )
②的对应角为( )
③的对应角为( )
④的对应边为( )
⑤的对应边为( )
⑥的对应边为( )
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
针对训练3
1.如图,,下列结论:①与是对应边;②与是对应边;③与是对应角;④与是对应角.其中正确的有( )
A.①③ B.②③ C.①④ D.②④
2.如图所示,,C,D是对应点,下列结论错误的是( )
A.与是对应角 B.与是对应角
C.与是对应边 D.与是对应边
3.如图,,和是对应角,AB和AC是对应边.写出其他对应边及对应角.
.
4.如图,,和CD,BC和DA是对应边.写出其他对应边及对应角.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
.
题型4 全等三角形的性质
例4.如图,,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
针对训练4
1.如图,已知,若,,则的长为( )
A.6 B.8 C.10 D.12
2.已知图中的两个三角形全等,则等于( )
A. B. C. D.
3.如图,,点E在AB上,AC与BD交于点F,,,,.
(1)求AE的长度;
(2)求的度数.
4.如图,已知,点E在上,与相交于点F.
(1)若,,求线段的长;
(2)已知,,求的度数.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
.
易错易混诠释
1.在图形中不能区分对应边和对应角,
复合变换(如平移、旋转、对称)后的图形,需准确标记对应点及边。
针对训练1
1.如图,,点和是对应点,点和是对应点,则的对应角是( )
A. B. C. D.
2.如图,,和,和是对应边,则的对应角是( )
A. B. C. D.
2.格式规范问题:书写顺序错误
针对训练2
1.若,则的对应边是 .
3.周长相等条件误用错误套用等式性质
针对训练3
1.如图,,若,,,则的周长等于 .
2.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.若两个图形周长相等,则它们一定是全等图形
C.两个等边三角形一定是全等图形
D.能够完全重合的两个图形是全等图形
创新拓展能力提升
1.将下图分成四个全等的图形,而且每一份图形中恰好有“巧分图形”四个字.
2.(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
①写出图中一对全等的三角形,并写出它们的所有对应角;
②设的度数为x,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.
3.如图,长方形中,cm,cm,现有一动点P从A出发以2cm/秒的速度,沿长方形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒.
(1)当秒时, cm;
(2)Q为边上的点,且,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与全等.
4.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.
(1)求证:∠ACD=∠B;
(2)若∠A=40°,求∠BCD的度数.
2025年新八年级数学人教版暑假大讲堂
第九讲 全等三角形及其性质
知识点梳理
知识点1 全等图形
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
要点诠释:
在平面几何中,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
知识点2 全等三角形
能够完全重合的两个三角形叫全等三角形.
要点诠释:
用符号“≌”表示,如△ABC ≌ △A'B'C',对应顶点字母写在对应位置.
隐含等量元素 :公共边、对顶角、平行线同位角等
知识点3 对应边、对应角和对应顶点
对应边、对应角、对应顶点的定义:
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
1.在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
2. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
知识点4 全等三角形的性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
要点诠释:
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
题型1 图形的全等
例1.嘉嘉、淇淇和笑笑在学习全等三角形时,关于“全等形”提出了三种不同的说法.
嘉嘉说:形状、大小相同的图形是全等形.
淇淇说:能够完全重合的图形是全等形.
笑笑说:各边都相等的图形是全等形.
他们的说法中,正确的有( )
A.0个 B.1个 C.2个 D.3个
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
答案:C
解析:嘉嘉说:形状、大小相同的图形是全等形,正确,符合题意.
淇淇说:能够完全重合的图形是全等形,正确,符合题意.
笑笑说:各边都相等的图形是全等形,不一定正确,因为相等两边的夹角不一定相等,不符合题意.
故选:C.
针对训练1
1.下列各组图形全等的是( )
A. B.
C. D.
答案:C
解析:能够完全重合的两个平面图形,叫全等图形,故A、B、D都不符合题意。
故选C
2.下列选项中能够表示两个全等图形的是( )
A.形状相同的两个图形 B.能够完全重合的两个图形
C.面积相等的两个图形 D.周长相等的两个图形
答案:B
解析:A、形状相同的两个图形,大小不一定相同,故此选项错误,不符合题意;
B、能够完全重合的两个图形是全等图形,故此选项正确,符合题意;
C、面积相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
D、周长相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
故选:B.
3.下列图形中,是全等图形的是( )
A.a,b,c,d B.a与b C.b,c,d D.a与c
答案:D
解析:能够完全重合的两个平面图形,叫全等图形.
由图可知,a与c是全等图形.
故选:D.
4.下列汽车标志中,是由多个全等图形组成的有( )个
A.1 B.2 C.3 D.4
答案:C
解析:第一个图形中,三个椭圆不全等,不是全等图形,不符合题意;
第二个图形中,上下两部分图形大小形状相同,是全等图形,符合题意;
第三个图形中,三个菱形大小形状相同,是全等图形,符合题意;
第四个图形中,四个圆形大小形状相同,是全等图形,符合题意;
即是由多个全等图形组成的有3个,
故选:C.
题型2 将已知图形分割成几个全等图形
例2.如图1,把大小为的正方形网格分割成了两个全等形.请在图2中,沿着虚线画出四种不同的分割方法,把的正方形网格分割成两个全等形.
等面积分割 :先确保分割后各子图面积相等,再调整形状使其全等。
逐步细分 :复杂图形可先分割为简单全等图形,再对子图进行细分(如矩形分割为两个全等矩形后,再各自分割)。
组合图形 :需先拆分基础图形,再寻找对称或等面积关系。
实际操作 :可通过物理方法(如重心平衡)辅助确定分割线。
答案:见解析
解析:要求分成全等的两块,
每块图形要包含有8个小正方形.
针对训练2
1.如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图1中给出了一种设计方案,请在图2、图3和图4中再画出两种不同的设计方案.
答案:图见解析
解析:方案如下.(答案不唯一,合理即可)
2.如图,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(至少画出两种)
答案:图见解析
解析:如图.(答案不唯一)
3.沿图中的虚线画线,把下面的图形划分为两个全等的图形(用二种不同方法):
答案:见解析
解析:如图所示:
4.如图,将图形分成大小、形状相同的三块,并且每块带一个☆.
答案:见解析
解析:如下图所示,将图形分成大小、形状相同的三块,并且每块带一个☆,
题型3 全等三角形对应元素
例3.如图,,请写出对应角,对应边.
①的对应角为( )
②的对应角为( )
③的对应角为( )
④的对应边为( )
⑤的对应边为( )
⑥的对应边为( )
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
答案:见解析
解析:①的对应角为,
②的对应角为,
③的对应角为,
④的对应边为,
⑤对应边为,
⑥的对应边为.
针对训练3
1.如图,,下列结论:①与是对应边;②与是对应边;③与是对应角;④与是对应角.其中正确的有( )
A.①③ B.②③ C.①④ D.②④
答案:B
解析:由得:
①与是对应边,故①不符合题意;
②与是对应边,故②符合题意;
③与是对应角,故③符合题意;
④与是对应角,与是对应角,故④不符合题意;
故正确的有②③,
故选:B.
2.如图所示,,C,D是对应点,下列结论错误的是( )
A.与是对应角 B.与是对应角
C.与是对应边 D.与是对应边
答案:C
解析:,
,,,
A,B,D选项正确,不符合题意,
故选:C.
3.如图,,和是对应角,AB和AC是对应边.写出其他对应边及对应角.
答案:见解析
解析:对应边:AN与AM,BN与CM.
对应角:与,与.
4.如图,,和CD,BC和DA是对应边.写出其他对应边及对应角.
答案:见解析
解析:对应边:AC与CA.
对应角:与,与,与.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
答案:(1)见解析
(2)
解析:(1)对应边:AE与AD,EC与DB,AC与AB.
对应角:与,与,与.
(2)因为,,
所以.
又因为在中,,,
,,,
所以.
题型4 全等三角形的性质
例4.如图,,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;
全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
答案:(1)见解析
(2)35°
解析:(1)证明:,
,
即,
;
(2),,
,
,
,
,,
.
针对训练4
1.如图,已知,若,,则的长为( )
A.6 B.8 C.10 D.12
答案:B
解析:,
,
,
故选:B.
2.已知图中的两个三角形全等,则等于( )
A. B. C. D.
答案:D
解析:由全等三角形的性质得:是边a和c的夹角,
∴,
故选:D.
3.如图,,点E在AB上,AC与BD交于点F,,,,.
(1)求AE的长度;
(2)求的度数.
答案:(1)3
(2)
解析:(1),
,.
(2),
,,
.
4.如图,已知,点E在上,与相交于点F.
(1)若,,求线段的长;
(2)已知,,求的度数.
答案:(1)
(2)
解析:(1)∵,,,
∴,,
∴;
(2)∵,,,
∴,,,
∴,
∴,
∴,
∴.
5.如图,,点E和点D是对应顶点.
(1)写出它们的对应边和对应角;
(2)若,,且,求的度数.
答案:(1)见解析
(2)
解析:(1)对应边:AE与AD,EC与DB,AC与AB.
对应角:与,与,与.
(2)因为,,
所以.
又因为在中,,,
,,,
所以.
易错易混诠释
1.在图形中不能区分对应边和对应角,
复合变换(如平移、旋转、对称)后的图形,需准确标记对应点及边。
针对训练1
1.如图,,点和是对应点,点和是对应点,则的对应角是( )
A. B. C. D.
【答案】.B
【分析】本题考查了全等三角形的概念,根据全等三角形的概念即可判断,正确找出对应边,对应角是解题的关键.
【详解】解:∵,点和是对应点,点和是对应点,
∴的对应角是,
故选:.
2.如图,,和,和是对应边,则的对应角是( )
A. B. C. D.
【答案】B
【分析】本题主要考查全等三角形的概念,根据已知条件,和,和是对应边,点与点对应点,点与点是对应点,由此即可得到的对应角,理解其概念是解题的关键.
【详解】∵,
∴∠的对应角是,
故选:.
2.格式规范问题:书写顺序错误
针对训练2
1.若,则的对应边是 .
【答案】/
【分析】本题考查了全等三角形的概念,根据全等三角形的概念判断即可.
【详解】解:∵,
∴的对应边是,
故答案为:.
2.已知A与,B与是对应点,则和全等用符号语言表示为:
【答案】
【分析】本题主要考查了全等三角形的概念,根据全等三角形的概念求解即可.
【详解】解:A与,B与是对应点,则和全等用符号语言表示为,
故答案为:.
3.周长相等条件误用错误套用等式性质
针对训练3
1.如图,,若,,,则的周长等于 .
【答案】13
【分析】本题考查了全等三角形性质的运用,运用全等三角形的性质,找对对应边,即可得三边边长,然后根据三角形的周长公式求解即可.
【详解】解:∵,,
∴,,,
∴的周长为.
故答案为:13.
2.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形
B.若两个图形周长相等,则它们一定是全等图形
C.两个等边三角形一定是全等图形
D.能够完全重合的两个图形是全等图形
【答案】D
【分析】根据全等三角形的定义进行判断作答即可.
【详解】解:两个面积相等的图形,不一定是全等图形,A错误,故不符合要求;
若两个图形周长相等,则它们不一定是全等图形,B错误,故不符合要求;
两个等边三角形不一定是全等图形,C错误,故不符合要求;
能够完全重合的两个图形是全等图形,D正确,故符合要求;
故选:D.
【点睛】本题考查了全等三角形的定义.解题的关键在于对知识的熟练掌握.
创新拓展能力提升
1.将下图分成四个全等的图形,而且每一份图形中恰好有“巧分图形”四个字.
【答案】见解析.
【详解】试题分析:要分成四个全等的图形,且每个图形中恰好有“巧分图形”四个字,所以相同的字必须分开,由此分图即可.
试题解析:图(a)中共有36个小方格,平分成4份后,每份应是9个小方格;因为第一份中要有“巧分图形”四个字,所以相同的两个字必须分支;又因为分成的每一份一定要通过大正方形的中心点,所以正方形中间的四个小方格一定是分开的,其中有一块已有“巧”字,它的下面一格一定是与“图”字相连如图(b)
2.(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
①写出图中一对全等的三角形,并写出它们的所有对应角;
②设的度数为x,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.
【答案】(1)①△EAD≌△EA′D,其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;②∠1=180° 2x,∠2=180° 2y; ③∠A=(∠1+∠2);(2)变化,∠A=(∠2-∠1),见详解
【分析】(1)①根据翻折方法可得△ADE≌△A′DE;
②根据翻折方法可得∠AEA′=2x,∠ADA′=2y,再根据平角定义可得∠1=180°-2x,∠2=180°-2y;
③首先由∠1=180°-2x,2=180°-2y,可得x=90-∠1,y=90-∠2,再根据三角形内角和定理可得∠A=180°-x-y,再利用等量代换可得∠A=(∠1+∠2);
(2)根据折叠的性质和三角形内角和定理解答即可.
【详解】(1)①根据翻折的性质知△EAD≌△EA′D,
其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;
②)∵∠AED=x,∠ADE=y,
∴∠AEA′=2x,∠ADA′=2y,
∴∠1=180°-2x,∠2=180°-2y;
③∠A=(∠1+∠2);
∵∠1=180°-2x,∠2=180°-2y,
∴x=90-∠1,y=90-∠2,
∴∠A=180°-x-y=190-(90-∠1)-(90-∠2)=(∠1+∠2).
(2))∵△A′DE是△ADE沿DE折叠得到,
∴∠A′=∠A,
又∵∠AEA′=180°-∠2,∠3=∠A′+∠1,
∴∠A+∠AEA′+∠3=180°,
即∠A+180°-∠2+∠A′+∠1=180°,
整理得,2∠A=∠2-∠1.
∴∠A=(∠2-∠1).
【点睛】此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
3.如图,长方形中,cm,cm,现有一动点P从A出发以2cm/秒的速度,沿长方形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒.
(1)当秒时, cm;
(2)Q为边上的点,且,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与全等.
【答案】(1)2
(2)2.5或4.5或7.5或9.5
【分析】(1)当秒时,点P运动到线段上,即可得到的长度;
(2)根据题意,要使一个三角形与全等,则点P的位置可以有四个,根据点P运动的位置,即可计算出时间.
【详解】(1)解:当t=3秒时,点P走过的路程为:,
∵,
∴点P运动到线段上,
∴cm,
故答案是:2;
(2)根据题意,如图,连接,则,,,
∴要使一个三角形与全等,则另一条直角边必须等于,
①当点P运动到时,,此时,
∴点P的路程为:,
∴,
②当点P运动到时,,此时,
∴点P的路程为:,
∴,
③当点P运动到时,,此时,
∴点P的路程为:,
∴,
④当点P运动到时,即P与Q重合时,,此时,
∴点P的路程为:,
∴,
综上所述,时间的值可以是:t=2.5s,4.5s,7.5s或9.5s.
【点睛】本题考查了全等三角形的判定与性质,线段的动点问题,等腰三角形的判定,解题的关键是掌握全等三角形的判定与性质及动点的运动状态,从而进行分类讨论.
4.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.
(1)求证:∠ACD=∠B;
(2)若∠A=40°,求∠BCD的度数.
【答案】(1)证明见解析;(2)140°.
【详解】试题分析:(1)根据平行线的性质可得∠ACB=∠DEC,∠ACD=∠D,再由∠ACD=∠B可得∠D=∠B,然后可利用AAS证明△ABC≌△CDE,进而得到CB=DE;
(2)根据全等三角形的性质可得∠A=∠DCE=40°,然后根据邻补角的性质进行计算即可.
试题解析:(1)证明:∵AC∥DE, ∴∠ACB=∠E,∠ACD=∠D,在△ACB和△CDB中,,∴△ABC≌△CDE,∴∠B=∠D,∴∠ACD=∠B
(2)解:∵△ABC≌△CDE, ∴∠A=∠DCE=40°,∴∠BCD=180°﹣∠ECD=140°.
点睛:此题主要考查了全等三角形的性质和判定,关键是掌握全等三角形的性质证明线段和角相等的重要工具.
典例精讲
名师支招
名师支招
名师支招
名师支招
典例精讲
名师支招
变式训练1
名师支招
名师支招
名师支招
试卷第1页,共3页
试卷第1页,共3页
同课章节目录
