第二十四章《圆》综合素质评价(含答案)
文档属性
| 名称 | 第二十四章《圆》综合素质评价(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:14:41 | ||
图片预览


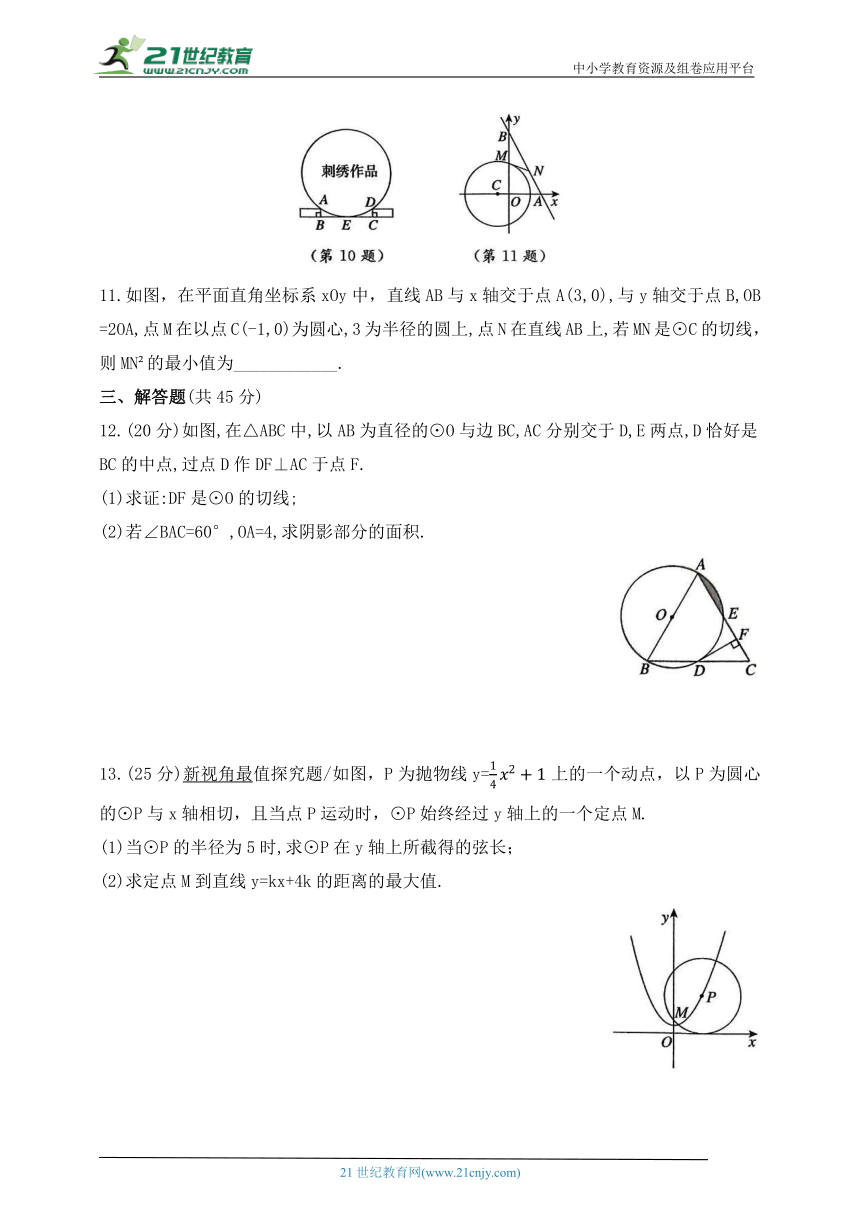
文档简介
中小学教育资源及组卷应用平台
第二十四章综合素质评价
[时间:60分钟 分值:100分]
一、选择题(每题5分,共35分)
1.已知⊙O的直径为10cm,若点P到圆心的距离是4cm,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
2.如图,以O为圆心的C,D三等分连接MN,CD,下列结论错误的是( )
A.∠COM=∠COD B.若OM=MN,则∠COD=20° C.MN∥CD D.MN=3CD
3.中国体育代表团在巴黎奥运会上取得了优异的成绩,图①是2024年巴黎奥运会的一枚金牌,金牌正中间镶嵌了一块来自埃菲尔铁塔的正六边形铁块.这个正六边形铁块的示意图如图②所示,已知该正六边形ABCDEF的周长约为18mm,则AD的长约为( )
4.中国的车轮制造,自古就有完备的标准体系.《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸,乘车之轮六尺有六寸……”如图,某学习小组通过以下方式探究某个残缺车轮的半径:在车轮上取A,B两点,设所在圆的圆心为O,经测量:弦AB=120cm,过弦AB的中点C作CD⊥AB交圆弧于点D,且CD=30cm,则该车轮的半径等于( )
A.90cm B.76cm C.30cm D.75cm
5.如图,⊙C过原点O,且与两坐标轴分别交于点A,B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为( )
A.6 B.5 C.3
6.某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆的周长为20πcm,母线AB长为30cm,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
A.30cm B.30cm C.60cm D.20πcm
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题5分,共20分)
8.如图,B,C,D是半径为6的⊙O上的三点,已知的长为2π,且OD∥BC,则BD的长为______________.
9.如图,在扇形AOB中,∠AOB=105°,半径OA=8,将扇形AOB沿过点B的直线折叠,点O恰好落在AB上的点D处,折痕交OA于点C,则图中阴影部分的面积是_____________.(结果保留π)
10.刺绣是我国独有的一门传统艺术,它承载着大量中国民族文化的意义.圆形刺绣作品展示木架的设计简图如图所示,已知AB,BC,CD分别与圆相交于点A,E,D,AB⊥BC,CD⊥BC,AB=CD=2cm,BC=12cm,则圆形刺绣作品的半径为__________cm.
11.如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(3,0),与y轴交于点B,OB=2OA,点M在以点C(-1,0)为圆心,3为半径的圆上,点N在直线AB上,若MN是⊙C的切线,则MN 的最小值为____________.
三、解答题(共45分)
12.(20分)如图,在△ABC中,以AB为直径的⊙O与边BC,AC分别交于D,E两点,D恰好是BC的中点,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若∠BAC=60°,OA=4,求阴影部分的面积.
13.(25分)新视角最值探究题/如图,P为抛物线y=上的一个动点,以P为圆心的⊙P与x轴相切,且当点P运动时,⊙P始终经过y轴上的一个定点M.
(1)当⊙P的半径为5时,求⊙P在y轴上所截得的弦长;
(2)求定点M到直线y=kx+4k的距离的最大值.
参考答案
一、1.A 2.D 3.A 4.D 5.C 6.B
7.D【点拨】∵E是△ABC的内心,∴AD平分∠BAC,∴∠BAD=∠CAD,故①正确;
如图,连接BE,CE.
∵E是△ABC的内心,
∵∠BAC=60°,∴∠ABC+∠ACB=120°.∠ACB)=120°,故②正确;
设△ABC的外接圆圆心为O,连接OD.
∵∠BAD=∠CAD,∴BD=DC.∴OD⊥BC.
∵点G为BC的中点,∴G一定为OD与BC的交点.∴∠BGD=90°,故③正确;
∵E是△ABC的内心,∴∠ABE=∠CBE.
∵∠DBC=∠DAC=∠BAD,∴∠DBC+∠EBC=∠EAB+∠EBA.
∴∠DBE=∠DEB.∴DB=DE,故④正确.
综上所述,正确的结论有①②③④,共4个.
二、8.6 10.10
11.【点拨】连接CM,CN,BC,如图,
∵A(3,0),∴OA=3.
∵OB=2OA,
∵MN是⊙C的切线,∴∠CMN=90°.
∴当CN最小时,MN最小,即CN⊥AB时CN最小.
∵C(-1,0),A(3,0),∴AC=4.
在△ABC中,
三、12.(1)【证明】如图,连接OD.
∵D是BC的中点,∴BD=CD.
∵OA=OB,∴OD是△ABC的中位线.∴OD∥AC.∴∠ODF=∠DFC.
∵DF⊥AC,∴∠DFC=90°.∴∠ODF=90°,即DF⊥OD.
又∵OD是⊙O的半径,∴DF是⊙O的切线.
(2)【解】如图,连接OE,则OE=OA=4.
∴△AOE是等边三角形.∴∠AOE=60°.
∴易得
13.【解】(1)设⊙P与y轴的另一个交点为N,连接PN,过点P作PH⊥y轴于点H,则
∵⊙P与x轴相切,解得
即点P的坐标为(4,5)或(-4,5).
即⊙P在y轴上所截得的弦长为6.
(2)设M(0,m),则⊙P的半径为即
即
整理得
∵无论点P如何运动,M为定点,∴与a值无关,即m=2.∴M(0,2).∵直线y=kx+4k经过定点(-4,0),设此点为Q,∴直线y=kx+4k绕点Q旋转到与MQ垂直时,定点M到该直线的距离最大,最大值为MQ的长,即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章综合素质评价
[时间:60分钟 分值:100分]
一、选择题(每题5分,共35分)
1.已知⊙O的直径为10cm,若点P到圆心的距离是4cm,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
2.如图,以O为圆心的C,D三等分连接MN,CD,下列结论错误的是( )
A.∠COM=∠COD B.若OM=MN,则∠COD=20° C.MN∥CD D.MN=3CD
3.中国体育代表团在巴黎奥运会上取得了优异的成绩,图①是2024年巴黎奥运会的一枚金牌,金牌正中间镶嵌了一块来自埃菲尔铁塔的正六边形铁块.这个正六边形铁块的示意图如图②所示,已知该正六边形ABCDEF的周长约为18mm,则AD的长约为( )
4.中国的车轮制造,自古就有完备的标准体系.《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸,乘车之轮六尺有六寸……”如图,某学习小组通过以下方式探究某个残缺车轮的半径:在车轮上取A,B两点,设所在圆的圆心为O,经测量:弦AB=120cm,过弦AB的中点C作CD⊥AB交圆弧于点D,且CD=30cm,则该车轮的半径等于( )
A.90cm B.76cm C.30cm D.75cm
5.如图,⊙C过原点O,且与两坐标轴分别交于点A,B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为( )
A.6 B.5 C.3
6.某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆的周长为20πcm,母线AB长为30cm,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
A.30cm B.30cm C.60cm D.20πcm
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题5分,共20分)
8.如图,B,C,D是半径为6的⊙O上的三点,已知的长为2π,且OD∥BC,则BD的长为______________.
9.如图,在扇形AOB中,∠AOB=105°,半径OA=8,将扇形AOB沿过点B的直线折叠,点O恰好落在AB上的点D处,折痕交OA于点C,则图中阴影部分的面积是_____________.(结果保留π)
10.刺绣是我国独有的一门传统艺术,它承载着大量中国民族文化的意义.圆形刺绣作品展示木架的设计简图如图所示,已知AB,BC,CD分别与圆相交于点A,E,D,AB⊥BC,CD⊥BC,AB=CD=2cm,BC=12cm,则圆形刺绣作品的半径为__________cm.
11.如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(3,0),与y轴交于点B,OB=2OA,点M在以点C(-1,0)为圆心,3为半径的圆上,点N在直线AB上,若MN是⊙C的切线,则MN 的最小值为____________.
三、解答题(共45分)
12.(20分)如图,在△ABC中,以AB为直径的⊙O与边BC,AC分别交于D,E两点,D恰好是BC的中点,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若∠BAC=60°,OA=4,求阴影部分的面积.
13.(25分)新视角最值探究题/如图,P为抛物线y=上的一个动点,以P为圆心的⊙P与x轴相切,且当点P运动时,⊙P始终经过y轴上的一个定点M.
(1)当⊙P的半径为5时,求⊙P在y轴上所截得的弦长;
(2)求定点M到直线y=kx+4k的距离的最大值.
参考答案
一、1.A 2.D 3.A 4.D 5.C 6.B
7.D【点拨】∵E是△ABC的内心,∴AD平分∠BAC,∴∠BAD=∠CAD,故①正确;
如图,连接BE,CE.
∵E是△ABC的内心,
∵∠BAC=60°,∴∠ABC+∠ACB=120°.∠ACB)=120°,故②正确;
设△ABC的外接圆圆心为O,连接OD.
∵∠BAD=∠CAD,∴BD=DC.∴OD⊥BC.
∵点G为BC的中点,∴G一定为OD与BC的交点.∴∠BGD=90°,故③正确;
∵E是△ABC的内心,∴∠ABE=∠CBE.
∵∠DBC=∠DAC=∠BAD,∴∠DBC+∠EBC=∠EAB+∠EBA.
∴∠DBE=∠DEB.∴DB=DE,故④正确.
综上所述,正确的结论有①②③④,共4个.
二、8.6 10.10
11.【点拨】连接CM,CN,BC,如图,
∵A(3,0),∴OA=3.
∵OB=2OA,
∵MN是⊙C的切线,∴∠CMN=90°.
∴当CN最小时,MN最小,即CN⊥AB时CN最小.
∵C(-1,0),A(3,0),∴AC=4.
在△ABC中,
三、12.(1)【证明】如图,连接OD.
∵D是BC的中点,∴BD=CD.
∵OA=OB,∴OD是△ABC的中位线.∴OD∥AC.∴∠ODF=∠DFC.
∵DF⊥AC,∴∠DFC=90°.∴∠ODF=90°,即DF⊥OD.
又∵OD是⊙O的半径,∴DF是⊙O的切线.
(2)【解】如图,连接OE,则OE=OA=4.
∴△AOE是等边三角形.∴∠AOE=60°.
∴易得
13.【解】(1)设⊙P与y轴的另一个交点为N,连接PN,过点P作PH⊥y轴于点H,则
∵⊙P与x轴相切,解得
即点P的坐标为(4,5)或(-4,5).
即⊙P在y轴上所截得的弦长为6.
(2)设M(0,m),则⊙P的半径为即
即
整理得
∵无论点P如何运动,M为定点,∴与a值无关,即m=2.∴M(0,2).∵直线y=kx+4k经过定点(-4,0),设此点为Q,∴直线y=kx+4k绕点Q旋转到与MQ垂直时,定点M到该直线的距离最大,最大值为MQ的长,即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
