24.1 圆的有关性质 第1课时 圆 同步练习(含答案)
文档属性
| 名称 | 24.1 圆的有关性质 第1课时 圆 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 371.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.1 圆的有关性质
第1课时 圆
基础提优题
1.下列说法中:
①弦是直径; ②长度相等的两条弧是等弧; ③半圆是弧;
④过圆心的线段是直径; ⑤面积相等的两个圆是等圆.
其中错误的有( )
A.1个 B.2个 C.3个 D.4个
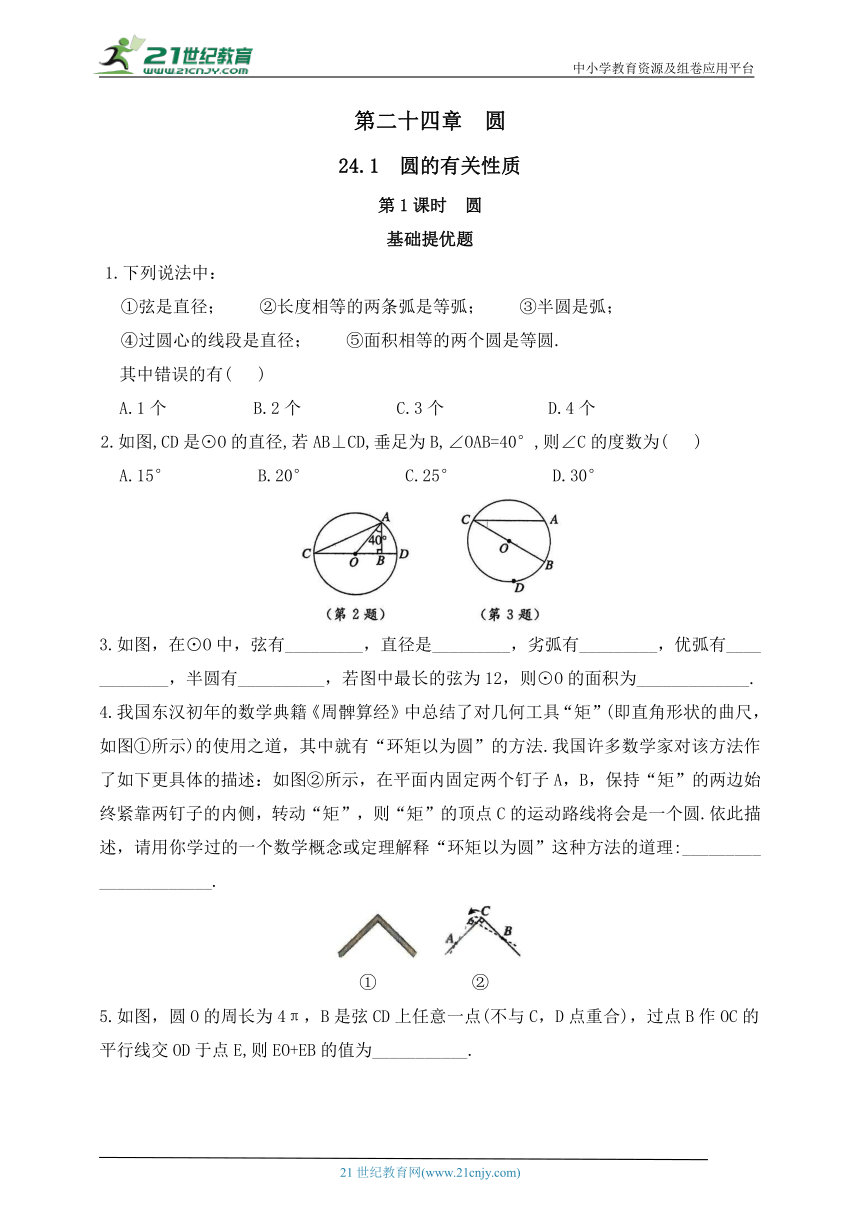
2.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C的度数为( )
A.15° B.20° C.25° D.30°
3.如图,在⊙O中,弦有_________,直径是_________,劣弧有_________,优弧有____________,半圆有__________,若图中最长的弦为12,则⊙O的面积为_____________.
4.我国东汉初年的数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图①所示)的使用之道,其中就有“环矩以为圆”的方法.我国许多数学家对该方法作了如下更具体的描述:如图②所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两钉子的内侧,转动“矩”,则“矩”的顶点C的运动路线将会是一个圆.依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:______________________.
① ②
5.如图,圆O的周长为4π,B是弦CD上任意一点(不与C,D点重合),过点B作OC的平行线交OD于点E,则EO+EB的值为___________.
6.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且 AB=OC.
(1)求∠AOB的度数;
(2)求∠EOD的度数.
综合应用题
7.如图,在⊙O中,C是上一点,OA⊥OB,过点C作弦CD交OB于点E,若OA=DE,则∠C与∠AOC满足的数量关系是( )
8.如图,将两个正方形如图放置(B,C,E共线,D,C,G共线),若AB=3,EF=2,点O在线段BC上,以点O为圆心作半圆O,点A、点F都在半圆O上,则OD的长是 ( )
A.4 C.
9.如图,在平面直角坐标系中,⊙I的圆心为(0,1),半径为1,直线经过定点A,交⊙I于一点M,则当MA取得最大值时,k的值为( )
A.-2 C.-3
10.已知P是⊙O内一点,点P不与圆心O重合,点P到圆上各点的距离中,最小距离与最大距离是关于x的一元二次方程0的两个实数根,则⊙O的半径为____________.
11.如图,海军某部队在灯塔A周围进行爆破作业,灯塔A周围3km内的水域为危险水域,有一渔船误入离灯塔A2km远的B处,为了尽快驶离危险区域,该渔船应按哪条射线方向航行 请说明理由.
12.如图,四边形ABCO是菱形,点A,B,C在⊙O上,若⊙O的半径是6,求弦AC的长,
创新拓展题
13.人教数学课本上有这样一道练习题:“△ABC中,∠C=90°.求证:A,B,C三点在同一个圆上”.下面我们进一步探究.
(1)如图①,BD,CE是△ABC的高,M是BC的中点,求证:点B,C,D,E在同一个圆上;
(2)如图②,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连接CG,求CG的最小值.
参考答案
1.C 2.C
3.AC,CB;CB;,,,,,,,,,
4.圆是所有到定点的距离等于定长的点的集合
5.2【点拨】∵圆O的周长为4π,∴OD=2.
∵OC=OD,∴∠C=∠D.∵BE∥OC,∴∠EBD=∠C.∴∠EBD=∠D.
∴BE=DE.∴EO+EB=OD=2.
6.【解】(1)∵AB=OC,OB=OC,∴AB=OB.∴∠AOB=∠A=20°
(2)∵∠OBE=∠A+∠AOB,∠AOB=∠A=20°,∴∠OBE=2∠A=40°.
∵OB=OE,∴∠OBE=∠E=40°.∴∠DOE=∠A+∠E=60°.
7.C【点拨】连接OD.∵OA=DE,∴OD=DE=OC.
∴∠C=
8.B【点拨】连接OA,OF.∵点A、点F都在半圆O上,∴OA=OF.
∵四边形ABCD,EFGC都是正方形,
∴∠ABC=∠DCB=∠FEC=90°,BC=CD=AB=3,CE=EF=2.
设OC=x,则BO=3-x,OE=x+2.
在Rt△ABO和Rt△EFO中,
又∵AO=FO,∴3 +解得x=1,即OC=1.
在Rt△DOC中,
9.D【点拨】本题考查了直线上点的坐标特征,圆外一点到圆上点距离的最大值.由题意知,当圆心I在线段AM上时,MA取得最大值,把点I的坐标代入中,即可求得k的值.
10.6【点拨】本题考查了一元二次方程根与系数的关系,点与圆上各点的距离的最值,明确最小距离与最大距离的和等于圆的直径是解题关键.由根与系数的关系求出两根之和,即可得到圆的直径,进而得到圆的半径.
11.【解】该渔船应按射线AB方向航行,驶离危险区域.
理由:连接AB并延长交⊙A于点C,在⊙A上任取一点D(点D异于点C).
①当点D异于点C关于点A的对称点时,连接BD,AD.在△ABD中,AB+BD>AD.
∵AD=AC=AB+BC,∴AB+BD>AB+BC,∴BD>BC;
②当点D为点C关于点A的对称点时,连接AD.
∵BD=BA+AD=BA+AC,BC=AC-AB,∴BD>BC.
综上,该渔船应按射线AB方向航行,行驶路程最短,能尽快驶离危险区域.
个点方法本题运用了建模思想,将实际问题转化为数学问题.其中圆内一点到圆上的点的最小距离为以圆心为端点,过该点的射线与圆相交的点与该点之间的距离.
12.【解】连接OB,交AC于点D.
∵四边形ABCO是菱形,∴OB⊥AC,AC=2AD,OB=2OD.
∵OA=OB=6,∴OD=3.
13.(1)【证明】如图①,连接ME,MD,∵BD,CE分别是△ABC的高,M为BC的中点,∴ME=MD=MC=MB=BC.∴点B,C,D,E在以点M为圆心的同一个圆上.
(2)【解】如图②,取AB的中点O,连接OC,OG,则OG=∴根据题意,G点的轨迹是以点O为圆心,AO为半径的圆弧.∴OC和OG的长度是一定的,因此当O,G,C三点在同一条直线上时,CG取最小值.
∵正方形ABCD的边长为2,∴∠ABC=90°,BC=AB=2.
∵点O是AB的中点,∴OB=OG=1.∴OC=,∴CG的最小值为
点方法 隐圆问题:有时候,题目条件中没有直接给出圆的信息,而是将其隐藏在题目中,要通过分析和转化,发现或构造圆,我们把这类问题称为隐圆问题.根据圆的定义,到定点的距离等于定长的点都在同一个圆上,利用“直角三角形斜边上的中线等于斜边的一半”,我们可以得知直角三角形的三个顶点在同一个圆上,进而得到共斜边的两个直角三角形四个顶点共圆.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.1 圆的有关性质
第1课时 圆
基础提优题
1.下列说法中:
①弦是直径; ②长度相等的两条弧是等弧; ③半圆是弧;
④过圆心的线段是直径; ⑤面积相等的两个圆是等圆.
其中错误的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C的度数为( )
A.15° B.20° C.25° D.30°
3.如图,在⊙O中,弦有_________,直径是_________,劣弧有_________,优弧有____________,半圆有__________,若图中最长的弦为12,则⊙O的面积为_____________.
4.我国东汉初年的数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图①所示)的使用之道,其中就有“环矩以为圆”的方法.我国许多数学家对该方法作了如下更具体的描述:如图②所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两钉子的内侧,转动“矩”,则“矩”的顶点C的运动路线将会是一个圆.依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:______________________.
① ②
5.如图,圆O的周长为4π,B是弦CD上任意一点(不与C,D点重合),过点B作OC的平行线交OD于点E,则EO+EB的值为___________.
6.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且 AB=OC.
(1)求∠AOB的度数;
(2)求∠EOD的度数.
综合应用题
7.如图,在⊙O中,C是上一点,OA⊥OB,过点C作弦CD交OB于点E,若OA=DE,则∠C与∠AOC满足的数量关系是( )
8.如图,将两个正方形如图放置(B,C,E共线,D,C,G共线),若AB=3,EF=2,点O在线段BC上,以点O为圆心作半圆O,点A、点F都在半圆O上,则OD的长是 ( )
A.4 C.
9.如图,在平面直角坐标系中,⊙I的圆心为(0,1),半径为1,直线经过定点A,交⊙I于一点M,则当MA取得最大值时,k的值为( )
A.-2 C.-3
10.已知P是⊙O内一点,点P不与圆心O重合,点P到圆上各点的距离中,最小距离与最大距离是关于x的一元二次方程0的两个实数根,则⊙O的半径为____________.
11.如图,海军某部队在灯塔A周围进行爆破作业,灯塔A周围3km内的水域为危险水域,有一渔船误入离灯塔A2km远的B处,为了尽快驶离危险区域,该渔船应按哪条射线方向航行 请说明理由.
12.如图,四边形ABCO是菱形,点A,B,C在⊙O上,若⊙O的半径是6,求弦AC的长,
创新拓展题
13.人教数学课本上有这样一道练习题:“△ABC中,∠C=90°.求证:A,B,C三点在同一个圆上”.下面我们进一步探究.
(1)如图①,BD,CE是△ABC的高,M是BC的中点,求证:点B,C,D,E在同一个圆上;
(2)如图②,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连接CG,求CG的最小值.
参考答案
1.C 2.C
3.AC,CB;CB;,,,,,,,,,
4.圆是所有到定点的距离等于定长的点的集合
5.2【点拨】∵圆O的周长为4π,∴OD=2.
∵OC=OD,∴∠C=∠D.∵BE∥OC,∴∠EBD=∠C.∴∠EBD=∠D.
∴BE=DE.∴EO+EB=OD=2.
6.【解】(1)∵AB=OC,OB=OC,∴AB=OB.∴∠AOB=∠A=20°
(2)∵∠OBE=∠A+∠AOB,∠AOB=∠A=20°,∴∠OBE=2∠A=40°.
∵OB=OE,∴∠OBE=∠E=40°.∴∠DOE=∠A+∠E=60°.
7.C【点拨】连接OD.∵OA=DE,∴OD=DE=OC.
∴∠C=
8.B【点拨】连接OA,OF.∵点A、点F都在半圆O上,∴OA=OF.
∵四边形ABCD,EFGC都是正方形,
∴∠ABC=∠DCB=∠FEC=90°,BC=CD=AB=3,CE=EF=2.
设OC=x,则BO=3-x,OE=x+2.
在Rt△ABO和Rt△EFO中,
又∵AO=FO,∴3 +解得x=1,即OC=1.
在Rt△DOC中,
9.D【点拨】本题考查了直线上点的坐标特征,圆外一点到圆上点距离的最大值.由题意知,当圆心I在线段AM上时,MA取得最大值,把点I的坐标代入中,即可求得k的值.
10.6【点拨】本题考查了一元二次方程根与系数的关系,点与圆上各点的距离的最值,明确最小距离与最大距离的和等于圆的直径是解题关键.由根与系数的关系求出两根之和,即可得到圆的直径,进而得到圆的半径.
11.【解】该渔船应按射线AB方向航行,驶离危险区域.
理由:连接AB并延长交⊙A于点C,在⊙A上任取一点D(点D异于点C).
①当点D异于点C关于点A的对称点时,连接BD,AD.在△ABD中,AB+BD>AD.
∵AD=AC=AB+BC,∴AB+BD>AB+BC,∴BD>BC;
②当点D为点C关于点A的对称点时,连接AD.
∵BD=BA+AD=BA+AC,BC=AC-AB,∴BD>BC.
综上,该渔船应按射线AB方向航行,行驶路程最短,能尽快驶离危险区域.
个点方法本题运用了建模思想,将实际问题转化为数学问题.其中圆内一点到圆上的点的最小距离为以圆心为端点,过该点的射线与圆相交的点与该点之间的距离.
12.【解】连接OB,交AC于点D.
∵四边形ABCO是菱形,∴OB⊥AC,AC=2AD,OB=2OD.
∵OA=OB=6,∴OD=3.
13.(1)【证明】如图①,连接ME,MD,∵BD,CE分别是△ABC的高,M为BC的中点,∴ME=MD=MC=MB=BC.∴点B,C,D,E在以点M为圆心的同一个圆上.
(2)【解】如图②,取AB的中点O,连接OC,OG,则OG=∴根据题意,G点的轨迹是以点O为圆心,AO为半径的圆弧.∴OC和OG的长度是一定的,因此当O,G,C三点在同一条直线上时,CG取最小值.
∵正方形ABCD的边长为2,∴∠ABC=90°,BC=AB=2.
∵点O是AB的中点,∴OB=OG=1.∴OC=,∴CG的最小值为
点方法 隐圆问题:有时候,题目条件中没有直接给出圆的信息,而是将其隐藏在题目中,要通过分析和转化,发现或构造圆,我们把这类问题称为隐圆问题.根据圆的定义,到定点的距离等于定长的点都在同一个圆上,利用“直角三角形斜边上的中线等于斜边的一半”,我们可以得知直角三角形的三个顶点在同一个圆上,进而得到共斜边的两个直角三角形四个顶点共圆.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
