24.1 圆的有关性质 第5课时 圆周角定理(2) 同步练习(含答案)
文档属性
| 名称 | 24.1 圆的有关性质 第5课时 圆周角定理(2) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.1 圆的有关性质
第5课时 圆周角定理(2)
基础提优题
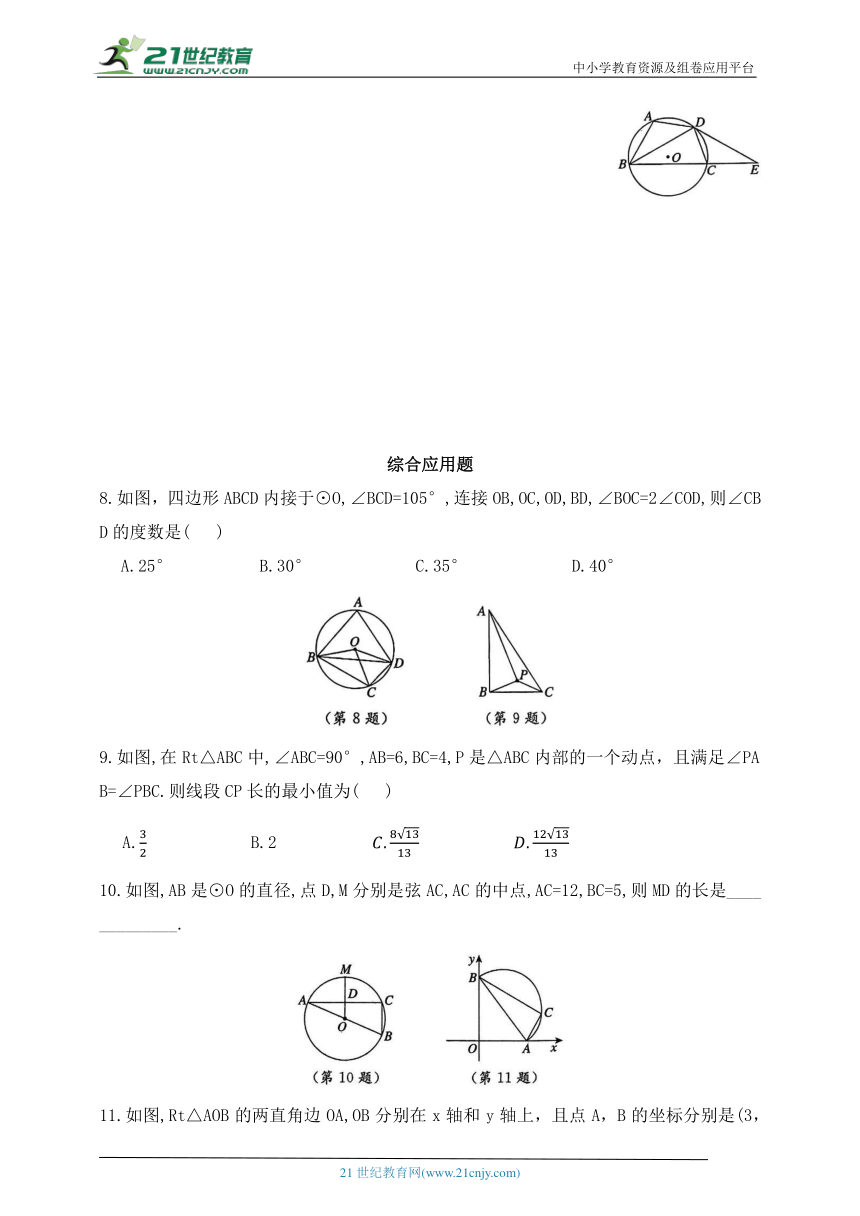
1.从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
2.如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD的度数为( )
A.70° B.60° C.50° D.30°
3.如图,AB为⊙O的直径,点C,D在⊙O上,若∠ADC=130°,则∠BAC的度数为 ( )
A.25° B.40° C.45° D.50°
4.如果一个圆内接四边形的三个内角度数之比为1:3:5,则第四个内角的度数是______________.
5.一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为_____________.
6.如图,⊙O是五边形ABCDE的外接圆,则∠B=_________.
7.如图,四边形ABCD内接于⊙O,D是.的中点,延长BC到点E,使CE=AB,连接BD,ED.
(1)求证:BD=ED;
(2)若∠ABC=60°,AD=5,求⊙O的半径.
综合应用题
8.如图,四边形ABCD内接于⊙O,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是( )
A.25° B.30° C.35° D.40°
9.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC.则线段CP长的最小值为( )
A. B.2
10.如图,AB是⊙O的直径,点D,M分别是弦AC,AC的中点,AC=12,BC=5,则MD的长是_____________.
11.如图,Rt△AOB的两直角边OA,OB分别在x轴和y轴上,且点A,B的坐标分别是(3,0)和(0,4),点C是半圆ACB上任意一点,连接AC,BC,则点O,C间的最大距离为______________.
12.如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,AD=BC,则AD+BC的值为____________.
13.如图,已知ED为⊙O的直径且ED=4,A(不与点E,D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线与AD的延长线交于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在⊙O上移动时,直接写出四边形FCDE的最大面积为多少.
创新拓展题
14.如图,四边形ABCD是半径为R的⊙O的内接四边形,AB是⊙O的直径,,直线与三条线段CD,CA,DA的延长线分别交于点E,F,G,且满足
(1)求证:直线⊥直线CE.
(2)若AB=DG.
①求证:△ABC≌△GDE;
②若求四边形ABCD的周长.
参考答案
1.C 2.B 3.B
4.90°或157.5°【点拨】设三个内角的度数为x,3x,5x,根据圆内接四边形的对角互补,得x+5x=180°,∴x=30°.∴第四个内角的度数是或:3x+5x=180°,∴x=22.5°.∴第四个内角的度数是
5.cm
6.116【点拨】连接AC,CE.
∵∠CAE+∠D=180°,∠D=128°,
∵∠AEC+∠B=180°,
7.(1)【证明】∵D是AC的中点,∴AD=DC.
∵四边形ABCD内接于⊙O,∴∠A+∠BCD=180°.
又∵∠ECD+∠BCD=180°,∴∠A=∠ECD.
又∵AB=CE,∴△ABD≌△CED(SAS).∴BD=ED.
(2)【解】如图,连接DO并延长交⊙O于点F,连接CF,则∠FCD=90°.
∴∠ABD=∠CBD,AD=CD=5.
又∵∠ABC=60°,∴∠CBD=30°.∴∠F=30°.∴DF=2CD=10.
∴⊙O的半径为
8.A【点拨】∵四边形ABCD内接于⊙O,∠BCD=105°,∴∠A=180°-105°=75°.∴∠BOD=2∠A=150°.
又∵∠BOC=2∠COD,∴∠COD=∠BOD=50°.
9.B【点拨】∵∠PAB=∠PBC,∠PBC+∠ABP=90°,∴∠PAB+∠ABP=90°.
∴∠APB=90°.取AB的中点O,则点P在以AB长为直径的⊙O上.
当点O,P,C三点共线时,线段CP最短,连接OC.
在Rt△OBC中,
又∴线段CP长的最小值为5-3=2.
10.4【点拨】∵M是AC的中点,∴OM⊥AC.
∵AB是⊙O的直径,∴∠C=90°.
∵AC=12,BC=5,∴AB= +5 =13.∴OM=6.5.
∵D是弦AC的中点,O是直径AB的中点,∴OD是△ABC的中位线.
∥BC.∴OD⊥AC.∴O,D,M三点共线.
∴MD=OM-OD=6.5-2.5=4.
11.5
12.10【点拨】如图,连接BO并延长,与⊙O交于点E,连接CE,DE.
∵BE是直径.∴∠BDE=∠BCE=90°,∴BD⊥DE.
又∵AC⊥BD,∴DE∥AC,∴∠CDE=B
BC.∴设EC=2k,BC=3k.
∵在Rt△BCE中,BC +
2或k=-2(舍去).∴BC=6,EC=4.∴AD=EC=4.
∴AD+BC=10,故答案为10.
13.(1)【证明】如图,连接FA.
∵DE是⊙O的直径,∴∠EAD=90°.
∵∠FEB=90°,∴EF⊥AB.∴∠FEA=90°.
∵BE=AE,EF⊥AB,∴EF为AB的垂直平分线.∴BF=AF.
∵∠FEA=90°,∴AF是⊙O的直径.∴AF=DE.∴BF=ED.
又∵EB=AE,∴Rt△EFB≌Rt△ADE(HL).
(2)【解】四边形FCDE的最大面积为8.
14.(1)【证明】由题意得∠ACD=∠ABD=45°.
∵在△CFE中,∠CFE=45°,
即直线⊥直线CE.
(2)①【证明】∵四边形ABCD是半径为R的⊙O的内接四边形,
∴∠ADC+∠ABC=180°.
又∵∠ADC+∠GDE=180°,∴∠ABC=∠GDE.
∵AB是⊙O的直径,∴∠ACB=90°.
由(1)可知∠GED=90°,∴∠ACB=∠GED.
在△ABC与△GDE中,∴△ABC≌△GDE.
②【解】∵在⊙O中,R=1,∴AB=2R=2.
∵AB是⊙O的直径,∴∠ADB=90°
∵∠ABD=45°,∴∠BAD=∠ABD=45°.∴DA=DB.
∴在Rt△ABD中,
即解得(负值已舍去).
由①知△ABC≌△GDE,∴BC=DE.
∴四边形ABCD的周长为DA+AB+BC+CD=DA+
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.1 圆的有关性质
第5课时 圆周角定理(2)
基础提优题
1.从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是( )
2.如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD的度数为( )
A.70° B.60° C.50° D.30°
3.如图,AB为⊙O的直径,点C,D在⊙O上,若∠ADC=130°,则∠BAC的度数为 ( )
A.25° B.40° C.45° D.50°
4.如果一个圆内接四边形的三个内角度数之比为1:3:5,则第四个内角的度数是______________.
5.一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为_____________.
6.如图,⊙O是五边形ABCDE的外接圆,则∠B=_________.
7.如图,四边形ABCD内接于⊙O,D是.的中点,延长BC到点E,使CE=AB,连接BD,ED.
(1)求证:BD=ED;
(2)若∠ABC=60°,AD=5,求⊙O的半径.
综合应用题
8.如图,四边形ABCD内接于⊙O,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是( )
A.25° B.30° C.35° D.40°
9.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC.则线段CP长的最小值为( )
A. B.2
10.如图,AB是⊙O的直径,点D,M分别是弦AC,AC的中点,AC=12,BC=5,则MD的长是_____________.
11.如图,Rt△AOB的两直角边OA,OB分别在x轴和y轴上,且点A,B的坐标分别是(3,0)和(0,4),点C是半圆ACB上任意一点,连接AC,BC,则点O,C间的最大距离为______________.
12.如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,AD=BC,则AD+BC的值为____________.
13.如图,已知ED为⊙O的直径且ED=4,A(不与点E,D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线与AD的延长线交于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在⊙O上移动时,直接写出四边形FCDE的最大面积为多少.
创新拓展题
14.如图,四边形ABCD是半径为R的⊙O的内接四边形,AB是⊙O的直径,,直线与三条线段CD,CA,DA的延长线分别交于点E,F,G,且满足
(1)求证:直线⊥直线CE.
(2)若AB=DG.
①求证:△ABC≌△GDE;
②若求四边形ABCD的周长.
参考答案
1.C 2.B 3.B
4.90°或157.5°【点拨】设三个内角的度数为x,3x,5x,根据圆内接四边形的对角互补,得x+5x=180°,∴x=30°.∴第四个内角的度数是或:3x+5x=180°,∴x=22.5°.∴第四个内角的度数是
5.cm
6.116【点拨】连接AC,CE.
∵∠CAE+∠D=180°,∠D=128°,
∵∠AEC+∠B=180°,
7.(1)【证明】∵D是AC的中点,∴AD=DC.
∵四边形ABCD内接于⊙O,∴∠A+∠BCD=180°.
又∵∠ECD+∠BCD=180°,∴∠A=∠ECD.
又∵AB=CE,∴△ABD≌△CED(SAS).∴BD=ED.
(2)【解】如图,连接DO并延长交⊙O于点F,连接CF,则∠FCD=90°.
∴∠ABD=∠CBD,AD=CD=5.
又∵∠ABC=60°,∴∠CBD=30°.∴∠F=30°.∴DF=2CD=10.
∴⊙O的半径为
8.A【点拨】∵四边形ABCD内接于⊙O,∠BCD=105°,∴∠A=180°-105°=75°.∴∠BOD=2∠A=150°.
又∵∠BOC=2∠COD,∴∠COD=∠BOD=50°.
9.B【点拨】∵∠PAB=∠PBC,∠PBC+∠ABP=90°,∴∠PAB+∠ABP=90°.
∴∠APB=90°.取AB的中点O,则点P在以AB长为直径的⊙O上.
当点O,P,C三点共线时,线段CP最短,连接OC.
在Rt△OBC中,
又∴线段CP长的最小值为5-3=2.
10.4【点拨】∵M是AC的中点,∴OM⊥AC.
∵AB是⊙O的直径,∴∠C=90°.
∵AC=12,BC=5,∴AB= +5 =13.∴OM=6.5.
∵D是弦AC的中点,O是直径AB的中点,∴OD是△ABC的中位线.
∥BC.∴OD⊥AC.∴O,D,M三点共线.
∴MD=OM-OD=6.5-2.5=4.
11.5
12.10【点拨】如图,连接BO并延长,与⊙O交于点E,连接CE,DE.
∵BE是直径.∴∠BDE=∠BCE=90°,∴BD⊥DE.
又∵AC⊥BD,∴DE∥AC,∴∠CDE=B
BC.∴设EC=2k,BC=3k.
∵在Rt△BCE中,BC +
2或k=-2(舍去).∴BC=6,EC=4.∴AD=EC=4.
∴AD+BC=10,故答案为10.
13.(1)【证明】如图,连接FA.
∵DE是⊙O的直径,∴∠EAD=90°.
∵∠FEB=90°,∴EF⊥AB.∴∠FEA=90°.
∵BE=AE,EF⊥AB,∴EF为AB的垂直平分线.∴BF=AF.
∵∠FEA=90°,∴AF是⊙O的直径.∴AF=DE.∴BF=ED.
又∵EB=AE,∴Rt△EFB≌Rt△ADE(HL).
(2)【解】四边形FCDE的最大面积为8.
14.(1)【证明】由题意得∠ACD=∠ABD=45°.
∵在△CFE中,∠CFE=45°,
即直线⊥直线CE.
(2)①【证明】∵四边形ABCD是半径为R的⊙O的内接四边形,
∴∠ADC+∠ABC=180°.
又∵∠ADC+∠GDE=180°,∴∠ABC=∠GDE.
∵AB是⊙O的直径,∴∠ACB=90°.
由(1)可知∠GED=90°,∴∠ACB=∠GED.
在△ABC与△GDE中,∴△ABC≌△GDE.
②【解】∵在⊙O中,R=1,∴AB=2R=2.
∵AB是⊙O的直径,∴∠ADB=90°
∵∠ABD=45°,∴∠BAD=∠ABD=45°.∴DA=DB.
∴在Rt△ABD中,
即解得(负值已舍去).
由①知△ABC≌△GDE,∴BC=DE.
∴四边形ABCD的周长为DA+AB+BC+CD=DA+
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
