24.1 圆的有关证明 第2课时 垂直于弦的直径 同步练习(含答案)
文档属性
| 名称 | 24.1 圆的有关证明 第2课时 垂直于弦的直径 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 432.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:22:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.1 圆的有关证明
第2课时 垂直于弦的直径
基础提优题
1.下列说法中,正确的是( )
A.圆是轴对称图形,每一条直径都是它的对称轴
B.平分弦的直径必垂直于这条弦
C.垂直于弦的直线必过圆心
D.垂直平分弦的直线必平分这条弦所对的弧
2..如图,AB为⊙O的直径,C,D为⊙O上的两点,且C为的中点.若∠BAD=20°,则∠ACO的度数为( )
A.30° B.45° C.55° D.60°
3.石拱桥是中国传统的桥梁四大基本形式之一,是用天然石料作为主要建筑材料的拱桥,以历史悠久,形式优美,结构坚固等特点闻名于世,它的主桥是圆弧形.如图,某石拱桥的跨度AB(弧AB所对的弦的长)约为36m,拱高CD(弧AB的中点到弦AB的距离)约为6m,则弧AB所在圆的半径为( )
A.30m B.27m C.6 D.25m
4.如图,在平面直角坐标系xOy中,⊙A过原点O,分别交y轴、x轴于点B,C.若点B的坐标为(0,6),AB=5,则点C的坐标为____________.
5.⊙O的半径为5,弦AB∥CD,AB=6,D=8,则AB与CD间的距离为_________.
综合应用题
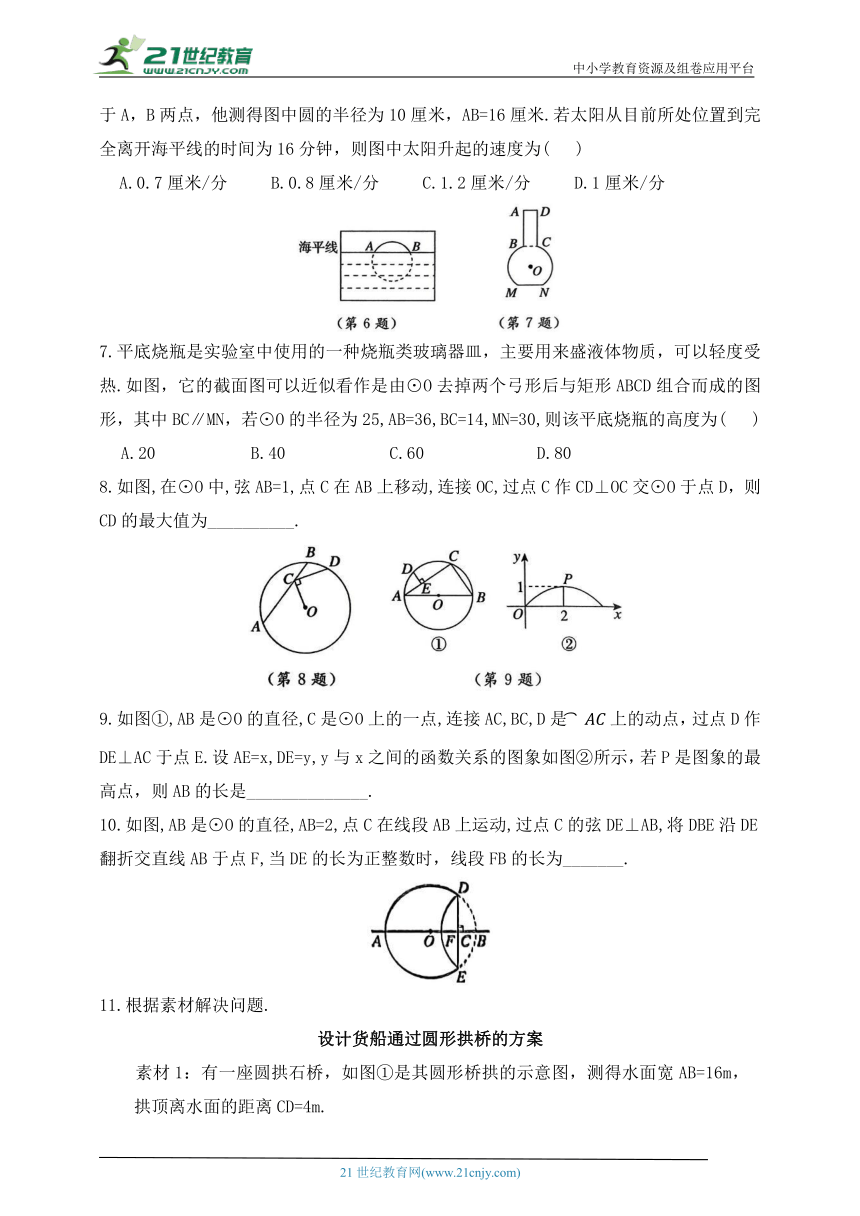
6.如图是一位同学从照片上剪下来的海上日出时的画面(示意图),图中太阳与海平线交于A,B两点,他测得图中圆的半径为10厘米,AB=16厘米.若太阳从目前所处位置到完全离开海平线的时间为16分钟,则图中太阳升起的速度为( )
A.0.7厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1厘米/分
7.平底烧瓶是实验室中使用的一种烧瓶类玻璃器皿,主要用来盛液体物质,可以轻度受热.如图,它的截面图可以近似看作是由⊙O去掉两个弓形后与矩形ABCD组合而成的图形,其中BC∥MN,若⊙O的半径为25,AB=36,BC=14,MN=30,则该平底烧瓶的高度为( )
A.20 B.40 C.60 D.80
8.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为__________.
9.如图①,AB是⊙O的直径,C是⊙O上的一点,连接AC,BC,D是上的动点,过点D作DE⊥AC于点E.设AE=x,DE=y,y与x之间的函数关系的图象如图②所示,若P是图象的最高点,则AB的长是______________.
10.如图,AB是⊙O的直径,AB=2,点C在线段AB上运动,过点C的弦DE⊥AB,将DBE沿DE翻折交直线AB于点F,当DE的长为正整数时,线段FB的长为_______.
11.根据素材解决问题.
设计货船通过圆形拱桥的方案
素材1:有一座圆拱石桥,如图①是其圆形桥拱的示意图,测得水面宽AB=16m,拱顶离水面的距离CD=4m.
素材2:如图②,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3m,EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(m)与货船增加的载重量x(t)满足函数关系式为
问题解决
任务1:求圆形桥拱的半径长.
任务2:根据图②中的状态,货船能否通过圆形桥拱 若能,最多还能卸载多少吨货物 若不能,至少要增加多少吨货物才能通过
创新拓展题
12.在⊙O中,AB为直径,P是AB上一点,∠NPB=45°.
(1)如图①,若点P与圆心O重合,直接写出的值.
(2)如图②,若MP=1,NP=7,求的值.
(3)当点P在AB上运动时,(2)中的结论是否改变 若不变,求其值;若变化,求其变化的范围.
参考答案
1.D
点易错 (1)直径是线段,对称轴是直线,因此不能说“圆的对称轴是直径”,而应该说“圆的对称轴是直径所在的直线”.
(2)垂径定理中的“垂径”(垂直于弦的直径)不局限于直径,还可以是半径或过圆心的直线或线段,其本质是“过圆心”,注意垂径定理及其推论的不同,推论中有“不是直径”这几个字.
2.C【点拨】∵OC为⊙O的半径,C为AD的中点,∴OC⊥AD.
∵∠BAD=20°,∴∠AOC=90°-∠BAD=70°.
3.A
4.(8,0)【点拨】如图所示,连接AC,过点A作AE⊥y轴于点E,作AF⊥x轴于点F,∴四边形OEAF是矩形.∴AE=OF,OE=AF.
∵B(0,6),∴OB=6.
∵AE⊥OB,∴BE=BE=3.
在Rt△ABE中,
∵AB,AC是圆的半径,∴AB=AC.
在Rt△ABE和Rt△CAF中,∴Rt△ABE≌Rt△CAF.∴AE=CF=4.
∵AF⊥OC,∴OF=CF=4.∴OC=OF+CF=4+4=8.∴C(8,0).
5.7或1【点拨】当AB,CD在点O异侧时,如图,过点O作OE⊥AB于点E,延长EO,交CD于点F,连接OA,OC,则AE=BE.
∵AB∥CD,∴OF⊥CD.∴CF=DF.
∵AB=6,CD=8,∴AE=3,CF=4.
∴在Rt△OAE中,(
在Rt△OCF中,OF=
∴AB与CD之间的距离为OE+OF=7;当AB,CD在点O同侧时,
同理可得AB与CD之间的距离为OE-OF=1.
综上,AB与CD之间的距离为7或1.
点易错 在无图的题目中,要根据题意画出图形,思考要全面,避免忽略图的对称性而漏解.
6.D
7.D【点拨】如图,连接OB,OM,过点O作EF⊥BC,交BC于点E,交MN于点F.
∵BC∥MN,∴EF⊥MN,∴EF平分BC,MN.
∵BC=14,MN=30,∴BE=7,MF=15.
在Rt△BEO和Rt△MOF中,OB=OM=25,
由勾股定理得
∴该平底烧瓶的高度为AB+OE+OF=36+24+20=80.
8.【点拨】连接OD.设⊙O的半径为r.
∵CD⊥OC,
可知当OC的值最小时,CD的值最大,
易知当OC⊥AB时,OC最小,此时
∴CD的最大值为
9.6【点拨】本题主要考查动点函数图象问题和垂径定理,过点O作OH⊥AC于点G,交⊙O于点H,由题意可知此时AG=2,HG=1.设OG=a,则OA=OH=a+1.在Rt△AOG中,由勾股定理可列方程,求出得从而可求出AB.
或或2【点拨】∵AB为直径,DE为弦,∴DE≤AB.
∴当DE的长为正整数时,DE=1或2.
当DE=2时,即DE为直径.∵DE⊥AB,
∴将DBE沿DE翻折交直线AB于点F,此时F与点A重合.∴FB=2;
当DE=1,且点C在线段OB之间时,如图①,连接OD,则
∴由翻折可知
当DE=1,且点C在线段OA之间时,如图②,连接OD,
同理可得
综上,线段FB的长为或或2.
11.【解】任务1:由题意可得拱高CD垂直平分AB,则
记圆心为点O,则点O在CD的延长线上,连接AO,如图.
设圆形桥拱的半径为rm,则OD=(r-4)m,解得r=10,
即圆形桥拱的半径长为10m.
任务2:如图,当EH是⊙O的弦时,易知AB∥EH.
∵AB⊥CD,∴EH⊥CD.
记EH与OC的交点为M,连接OE,如图,则EM=
∵OC=10m,CD=4m,∴OD=OC-CD=6m.∴
∴货船不能通过圆形桥拱.
为了能顺利通过圆形桥拱,船在水面部分至少需要下降的高度为
∵船身下降的高度y(m)与货船增加的载重量x(t)满足的函数关系式为
∴当时,.
∴至少需要增加(的货物.
12.【解】
(2)如图①,作OH⊥MN于点H,连接ON,∴MH=NH=MP=4-1=3.
∵∠NPB=45°,∴易得OH=PH=3.在Rt△HON中,
(3)(2)中的结论不改变.
作OH⊥MN于点H,连接OM,如图②,设PM=a,PN=b,∴MH=NH=a+b.
∵∠NPB=45°,∴∠OPH=45°.∴易得
在Rt△OMH中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.1 圆的有关证明
第2课时 垂直于弦的直径
基础提优题
1.下列说法中,正确的是( )
A.圆是轴对称图形,每一条直径都是它的对称轴
B.平分弦的直径必垂直于这条弦
C.垂直于弦的直线必过圆心
D.垂直平分弦的直线必平分这条弦所对的弧
2..如图,AB为⊙O的直径,C,D为⊙O上的两点,且C为的中点.若∠BAD=20°,则∠ACO的度数为( )
A.30° B.45° C.55° D.60°
3.石拱桥是中国传统的桥梁四大基本形式之一,是用天然石料作为主要建筑材料的拱桥,以历史悠久,形式优美,结构坚固等特点闻名于世,它的主桥是圆弧形.如图,某石拱桥的跨度AB(弧AB所对的弦的长)约为36m,拱高CD(弧AB的中点到弦AB的距离)约为6m,则弧AB所在圆的半径为( )
A.30m B.27m C.6 D.25m
4.如图,在平面直角坐标系xOy中,⊙A过原点O,分别交y轴、x轴于点B,C.若点B的坐标为(0,6),AB=5,则点C的坐标为____________.
5.⊙O的半径为5,弦AB∥CD,AB=6,D=8,则AB与CD间的距离为_________.
综合应用题
6.如图是一位同学从照片上剪下来的海上日出时的画面(示意图),图中太阳与海平线交于A,B两点,他测得图中圆的半径为10厘米,AB=16厘米.若太阳从目前所处位置到完全离开海平线的时间为16分钟,则图中太阳升起的速度为( )
A.0.7厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1厘米/分
7.平底烧瓶是实验室中使用的一种烧瓶类玻璃器皿,主要用来盛液体物质,可以轻度受热.如图,它的截面图可以近似看作是由⊙O去掉两个弓形后与矩形ABCD组合而成的图形,其中BC∥MN,若⊙O的半径为25,AB=36,BC=14,MN=30,则该平底烧瓶的高度为( )
A.20 B.40 C.60 D.80
8.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为__________.
9.如图①,AB是⊙O的直径,C是⊙O上的一点,连接AC,BC,D是上的动点,过点D作DE⊥AC于点E.设AE=x,DE=y,y与x之间的函数关系的图象如图②所示,若P是图象的最高点,则AB的长是______________.
10.如图,AB是⊙O的直径,AB=2,点C在线段AB上运动,过点C的弦DE⊥AB,将DBE沿DE翻折交直线AB于点F,当DE的长为正整数时,线段FB的长为_______.
11.根据素材解决问题.
设计货船通过圆形拱桥的方案
素材1:有一座圆拱石桥,如图①是其圆形桥拱的示意图,测得水面宽AB=16m,拱顶离水面的距离CD=4m.
素材2:如图②,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3m,EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(m)与货船增加的载重量x(t)满足函数关系式为
问题解决
任务1:求圆形桥拱的半径长.
任务2:根据图②中的状态,货船能否通过圆形桥拱 若能,最多还能卸载多少吨货物 若不能,至少要增加多少吨货物才能通过
创新拓展题
12.在⊙O中,AB为直径,P是AB上一点,∠NPB=45°.
(1)如图①,若点P与圆心O重合,直接写出的值.
(2)如图②,若MP=1,NP=7,求的值.
(3)当点P在AB上运动时,(2)中的结论是否改变 若不变,求其值;若变化,求其变化的范围.
参考答案
1.D
点易错 (1)直径是线段,对称轴是直线,因此不能说“圆的对称轴是直径”,而应该说“圆的对称轴是直径所在的直线”.
(2)垂径定理中的“垂径”(垂直于弦的直径)不局限于直径,还可以是半径或过圆心的直线或线段,其本质是“过圆心”,注意垂径定理及其推论的不同,推论中有“不是直径”这几个字.
2.C【点拨】∵OC为⊙O的半径,C为AD的中点,∴OC⊥AD.
∵∠BAD=20°,∴∠AOC=90°-∠BAD=70°.
3.A
4.(8,0)【点拨】如图所示,连接AC,过点A作AE⊥y轴于点E,作AF⊥x轴于点F,∴四边形OEAF是矩形.∴AE=OF,OE=AF.
∵B(0,6),∴OB=6.
∵AE⊥OB,∴BE=BE=3.
在Rt△ABE中,
∵AB,AC是圆的半径,∴AB=AC.
在Rt△ABE和Rt△CAF中,∴Rt△ABE≌Rt△CAF.∴AE=CF=4.
∵AF⊥OC,∴OF=CF=4.∴OC=OF+CF=4+4=8.∴C(8,0).
5.7或1【点拨】当AB,CD在点O异侧时,如图,过点O作OE⊥AB于点E,延长EO,交CD于点F,连接OA,OC,则AE=BE.
∵AB∥CD,∴OF⊥CD.∴CF=DF.
∵AB=6,CD=8,∴AE=3,CF=4.
∴在Rt△OAE中,(
在Rt△OCF中,OF=
∴AB与CD之间的距离为OE+OF=7;当AB,CD在点O同侧时,
同理可得AB与CD之间的距离为OE-OF=1.
综上,AB与CD之间的距离为7或1.
点易错 在无图的题目中,要根据题意画出图形,思考要全面,避免忽略图的对称性而漏解.
6.D
7.D【点拨】如图,连接OB,OM,过点O作EF⊥BC,交BC于点E,交MN于点F.
∵BC∥MN,∴EF⊥MN,∴EF平分BC,MN.
∵BC=14,MN=30,∴BE=7,MF=15.
在Rt△BEO和Rt△MOF中,OB=OM=25,
由勾股定理得
∴该平底烧瓶的高度为AB+OE+OF=36+24+20=80.
8.【点拨】连接OD.设⊙O的半径为r.
∵CD⊥OC,
可知当OC的值最小时,CD的值最大,
易知当OC⊥AB时,OC最小,此时
∴CD的最大值为
9.6【点拨】本题主要考查动点函数图象问题和垂径定理,过点O作OH⊥AC于点G,交⊙O于点H,由题意可知此时AG=2,HG=1.设OG=a,则OA=OH=a+1.在Rt△AOG中,由勾股定理可列方程,求出得从而可求出AB.
或或2【点拨】∵AB为直径,DE为弦,∴DE≤AB.
∴当DE的长为正整数时,DE=1或2.
当DE=2时,即DE为直径.∵DE⊥AB,
∴将DBE沿DE翻折交直线AB于点F,此时F与点A重合.∴FB=2;
当DE=1,且点C在线段OB之间时,如图①,连接OD,则
∴由翻折可知
当DE=1,且点C在线段OA之间时,如图②,连接OD,
同理可得
综上,线段FB的长为或或2.
11.【解】任务1:由题意可得拱高CD垂直平分AB,则
记圆心为点O,则点O在CD的延长线上,连接AO,如图.
设圆形桥拱的半径为rm,则OD=(r-4)m,解得r=10,
即圆形桥拱的半径长为10m.
任务2:如图,当EH是⊙O的弦时,易知AB∥EH.
∵AB⊥CD,∴EH⊥CD.
记EH与OC的交点为M,连接OE,如图,则EM=
∵OC=10m,CD=4m,∴OD=OC-CD=6m.∴
∴货船不能通过圆形桥拱.
为了能顺利通过圆形桥拱,船在水面部分至少需要下降的高度为
∵船身下降的高度y(m)与货船增加的载重量x(t)满足的函数关系式为
∴当时,.
∴至少需要增加(的货物.
12.【解】
(2)如图①,作OH⊥MN于点H,连接ON,∴MH=NH=MP=4-1=3.
∵∠NPB=45°,∴易得OH=PH=3.在Rt△HON中,
(3)(2)中的结论不改变.
作OH⊥MN于点H,连接OM,如图②,设PM=a,PN=b,∴MH=NH=a+b.
∵∠NPB=45°,∴∠OPH=45°.∴易得
在Rt△OMH中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
