24.2 点和圆、直线和圆的位置关系 第1课时 点和圆的位置关系 同步练习(含答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 第1课时 点和圆的位置关系 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 428.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:24:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
第1课时 点和圆的位置关系
基础提优题
1.在Rt△ABC中,∠C=90°,BC=5,AC=12,以点B为圆心,12为半径画圆,则点A与⊙B的位置关系是( )
A.点A在⊙B外 B.点A在⊙B上 C.点A在⊙B内 D.无法确定
2.若用反证法证明“若,则”,则应先假设( )
3.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
4.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画出的圆的个数是( )
A.1 B.2 C.3 D.4
5.如图,X,Y,Z是某社区内的三栋楼,XY=40m,YZ=30m,XZ=50m.若在XZ中点M处建一个5G网络基站,该基站的覆盖半径为26m,则这三栋楼中在该基站覆盖范围内的是( )
A.X,Y,Z B.X,Z C.Y,Z D.Y
6.已知直线:y=x-4,点A(1,0),B(0,2),设点P为直线上一动点,当点P的坐标为_____________时,过P,A,B三点不能作出一个圆.
7.尺规作图:如图,已知△ABC.
(1)求作:△ABC的外接圆⊙O;
(2)若AC=4,∠B=30°,则△ABC的外接圆⊙O的半径为.
综合应用题
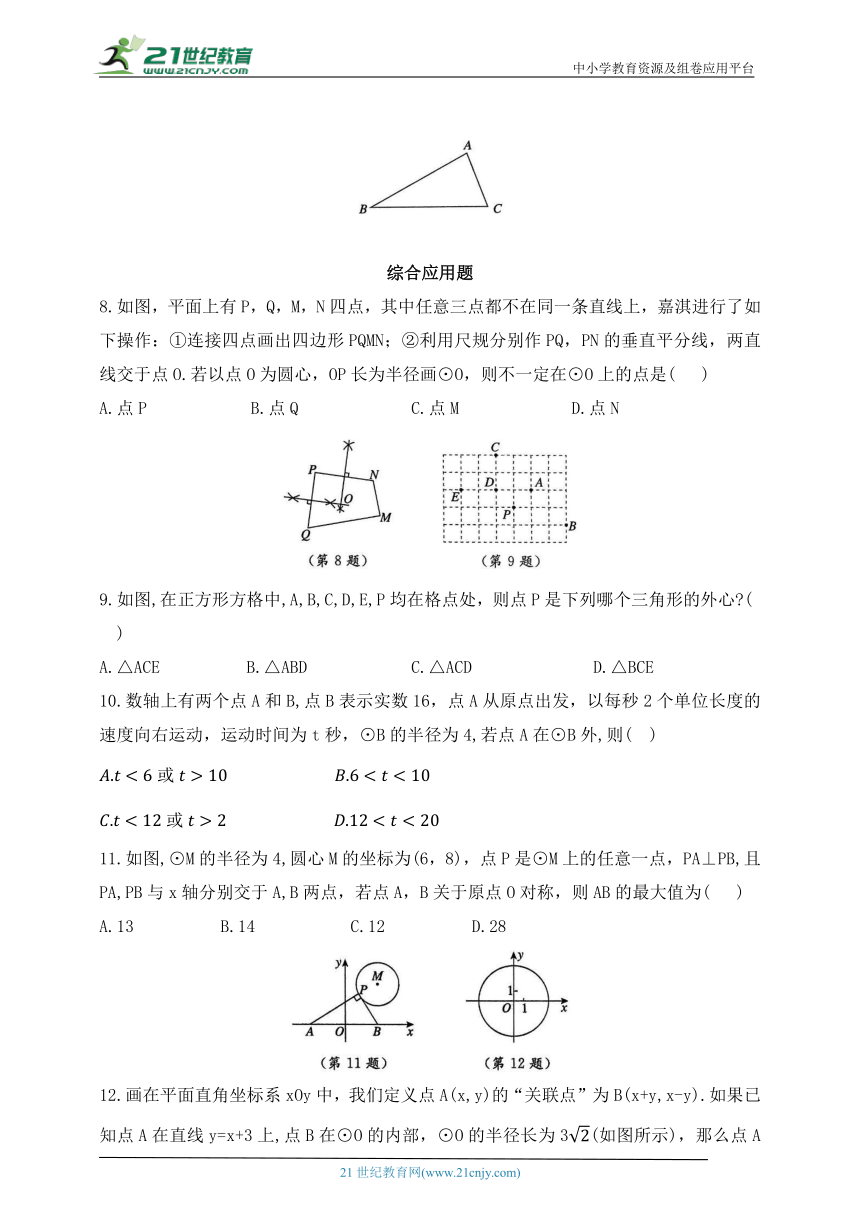
8.如图,平面上有P,Q,M,N四点,其中任意三点都不在同一条直线上,嘉淇进行了如下操作:①连接四点画出四边形PQMN;②利用尺规分别作PQ,PN的垂直平分线,两直线交于点O.若以点O为圆心,OP长为半径画⊙O,则不一定在⊙O上的点是( )
A.点P B.点Q C.点M D.点N
9.如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心 ( )
A.△ACE B.△ABD C.△ACD D.△BCE
10.数轴上有两个点A和B,点B表示实数16,点A从原点出发,以每秒2个单位长度的速度向右运动,运动时间为t秒,⊙B的半径为4,若点A在⊙B外,则( )
11.如图,⊙M的半径为4,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA,PB与x轴分别交于A,B两点,若点A,B关于原点O对称,则AB的最大值为( )
A.13 B.14 C.12 D.28
12.画在平面直角坐标系xOy中,我们定义点A(x,y)的“关联点”为B(x+y,x-y).如果已知点A在直线y=x+3上,点B在⊙O的内部,⊙O的半径长为3(如图所示),那么点A的横坐标x的取值范围是_____________.
13.如图,已知△ABC内接于⊙O,AB是直径,弦CE⊥AB于点F,C是.的中点,连接AD分别交CE,BC于点P,Q.求证:点P是△ACQ的外心.
14.如图,在矩形ABCD中,AB=3,AD=4,连接AC,BD.
(1)过点D作DF⊥AC于点F,过点A作AE⊥BD于点E,求AE,AF的长;
(2)以点A为圆心画圆,使B,C,D,E,F5个点中至少有1个点在圆内,且至少有2个点在圆外,并求⊙A的半径r的取值范围.
创新拓展题
15.BD,CE是△ABC的高,BD,CE相交于点F,M是BC的中点,⊙O是△ABC的外接圆.
(1)如图①,点B,C,D,E是否在以点M为圆心的同一个圆上 请说明理由.
(2)如图②,若AB=8,CF=6,求△ABC外接圆的半径长.
参考答案
1.A 2.D
3.B【点拨】如图,连接AB,BC,作AB和BC的垂直平分线,它们相交于点Q.故选B.
4C 5.A
6.(2.-2)【点拨】由题意可知,当P,A,B三点共线时,过这三点不能作出一个圆.设直线AB的解析式为y=kx+b,将点A(1,0),B(0,2)的坐标分别代入,得解得直线AB的解析式为y=-2x+2.解方程组得当点P的坐标为(2,-2)时,过P,A,B三点不能作出一个圆.
7.【解】(1)如图,⊙O即为所求作的圆.
(2)4
8.C【点拨】如图,连接OP,OQ,OM,ON.
∵作PQ,PN的垂直平分线,两直线交于点O,∴OP=OQ=ON,
∴点P,Q,N在以点O为圆心,OP长为半径的⊙O上.
∵OM与OP的大小关系不能确定.∴点M不一定在⊙O上.
9.D 10.A
11.D【点拨】如图,连接OP,∵PA⊥PB,∴∠APB=90°.
∵点A,B关于原点O对称,∴OA=OB,即O为AB的中点.∴AB=2OP.
若要使AB取最大值,则OP需取最大值,连接OM并延长,交⊙M于点P',当点P位于点P'时,OP取得最大值,
过点M作MQ⊥x轴于点Q,∵圆心M的坐标为(6,8),∴OQ=6,MQ=8.
又∵MP'=4,∴OP'=OM+MP'=14.∴OP的最大值为14.
∴AB的最大值为2×14=28.
12.-3∴x+y=x+x+3=2x+3,x-y=x-(x+3)=-3.∴点A(x,y)的“关联点”为B(2x+3,-3).当(,即点B在⊙O上时,,整理得x(x+3)=0,解得x =-3,x =0.∵点B在⊙O的内部,
13.【证明】∵AB是⊙O的直径,AB⊥CE,
∵C是AD的中点,.∴∠ACP=∠CAP.∴AP=PC.
∵∠QCP+∠ACP=∠CAP+∠CQP=90°,∴∠PCQ=∠CQP.∴CP=PQ.
∴CP=AP=PQ.∴点P是△ACQ的外心.
点方法 三角形外心的位置:锐角三角形的外心在三角形的内部;直角三角形的外心是斜边的中点;钝角三角形的外心在三角形的外部.
14.【解】(1)如图①所示.
∵在矩形ABCD中,AB=3,AD=4,
同理可得
在Rt△ADF中,
(2)画图答案不唯一,如图②所示.
由(1)可得AE若以点A为圆心画圆,B,C,D,E,F5个点中至少有1个点在圆内,且至少有2个点在圆外,则点E必在圆内,点D,C必在圆外.
∴⊙A的半径r的取值范围为
15.【解】(1)点B,C,D,E在以点M为圆心的同一个圆上,理由如下:
∵BD⊥AC,CE⊥AB,∴∠BEC=∠BDC=90°.
∴点D,E都在以BC为直径的圆上.
又∵M是BC的中点,∴点B,C,D,E在以点M为圆心的同一个圆上.
(2)如图,连接AF并延长交BC于点G,连接BO并延长交⊙O于点H,连接AH,CH.
∵BD,CE是△ABC的高,BD,CE相交于点F,∴AG⊥BC.
∵BH是⊙O的直径,∴∠BAH=∠BCH=90°.∴BA⊥AH,BC⊥CH.∴AG∥CH.
∵CE⊥AB,∴AH∥CE.∴四边形AFCH是平行四边形.∴AH=CF=6.
在Rt△BAH中,AB=8,AH=6,
∴△ABC外接圆的半径长为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
第1课时 点和圆的位置关系
基础提优题
1.在Rt△ABC中,∠C=90°,BC=5,AC=12,以点B为圆心,12为半径画圆,则点A与⊙B的位置关系是( )
A.点A在⊙B外 B.点A在⊙B上 C.点A在⊙B内 D.无法确定
2.若用反证法证明“若,则”,则应先假设( )
3.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
4.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画出的圆的个数是( )
A.1 B.2 C.3 D.4
5.如图,X,Y,Z是某社区内的三栋楼,XY=40m,YZ=30m,XZ=50m.若在XZ中点M处建一个5G网络基站,该基站的覆盖半径为26m,则这三栋楼中在该基站覆盖范围内的是( )
A.X,Y,Z B.X,Z C.Y,Z D.Y
6.已知直线:y=x-4,点A(1,0),B(0,2),设点P为直线上一动点,当点P的坐标为_____________时,过P,A,B三点不能作出一个圆.
7.尺规作图:如图,已知△ABC.
(1)求作:△ABC的外接圆⊙O;
(2)若AC=4,∠B=30°,则△ABC的外接圆⊙O的半径为.
综合应用题
8.如图,平面上有P,Q,M,N四点,其中任意三点都不在同一条直线上,嘉淇进行了如下操作:①连接四点画出四边形PQMN;②利用尺规分别作PQ,PN的垂直平分线,两直线交于点O.若以点O为圆心,OP长为半径画⊙O,则不一定在⊙O上的点是( )
A.点P B.点Q C.点M D.点N
9.如图,在正方形方格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心 ( )
A.△ACE B.△ABD C.△ACD D.△BCE
10.数轴上有两个点A和B,点B表示实数16,点A从原点出发,以每秒2个单位长度的速度向右运动,运动时间为t秒,⊙B的半径为4,若点A在⊙B外,则( )
11.如图,⊙M的半径为4,圆心M的坐标为(6,8),点P是⊙M上的任意一点,PA⊥PB,且PA,PB与x轴分别交于A,B两点,若点A,B关于原点O对称,则AB的最大值为( )
A.13 B.14 C.12 D.28
12.画在平面直角坐标系xOy中,我们定义点A(x,y)的“关联点”为B(x+y,x-y).如果已知点A在直线y=x+3上,点B在⊙O的内部,⊙O的半径长为3(如图所示),那么点A的横坐标x的取值范围是_____________.
13.如图,已知△ABC内接于⊙O,AB是直径,弦CE⊥AB于点F,C是.的中点,连接AD分别交CE,BC于点P,Q.求证:点P是△ACQ的外心.
14.如图,在矩形ABCD中,AB=3,AD=4,连接AC,BD.
(1)过点D作DF⊥AC于点F,过点A作AE⊥BD于点E,求AE,AF的长;
(2)以点A为圆心画圆,使B,C,D,E,F5个点中至少有1个点在圆内,且至少有2个点在圆外,并求⊙A的半径r的取值范围.
创新拓展题
15.BD,CE是△ABC的高,BD,CE相交于点F,M是BC的中点,⊙O是△ABC的外接圆.
(1)如图①,点B,C,D,E是否在以点M为圆心的同一个圆上 请说明理由.
(2)如图②,若AB=8,CF=6,求△ABC外接圆的半径长.
参考答案
1.A 2.D
3.B【点拨】如图,连接AB,BC,作AB和BC的垂直平分线,它们相交于点Q.故选B.
4C 5.A
6.(2.-2)【点拨】由题意可知,当P,A,B三点共线时,过这三点不能作出一个圆.设直线AB的解析式为y=kx+b,将点A(1,0),B(0,2)的坐标分别代入,得解得直线AB的解析式为y=-2x+2.解方程组得当点P的坐标为(2,-2)时,过P,A,B三点不能作出一个圆.
7.【解】(1)如图,⊙O即为所求作的圆.
(2)4
8.C【点拨】如图,连接OP,OQ,OM,ON.
∵作PQ,PN的垂直平分线,两直线交于点O,∴OP=OQ=ON,
∴点P,Q,N在以点O为圆心,OP长为半径的⊙O上.
∵OM与OP的大小关系不能确定.∴点M不一定在⊙O上.
9.D 10.A
11.D【点拨】如图,连接OP,∵PA⊥PB,∴∠APB=90°.
∵点A,B关于原点O对称,∴OA=OB,即O为AB的中点.∴AB=2OP.
若要使AB取最大值,则OP需取最大值,连接OM并延长,交⊙M于点P',当点P位于点P'时,OP取得最大值,
过点M作MQ⊥x轴于点Q,∵圆心M的坐标为(6,8),∴OQ=6,MQ=8.
又∵MP'=4,∴OP'=OM+MP'=14.∴OP的最大值为14.
∴AB的最大值为2×14=28.
12.-3
13.【证明】∵AB是⊙O的直径,AB⊥CE,
∵C是AD的中点,.∴∠ACP=∠CAP.∴AP=PC.
∵∠QCP+∠ACP=∠CAP+∠CQP=90°,∴∠PCQ=∠CQP.∴CP=PQ.
∴CP=AP=PQ.∴点P是△ACQ的外心.
点方法 三角形外心的位置:锐角三角形的外心在三角形的内部;直角三角形的外心是斜边的中点;钝角三角形的外心在三角形的外部.
14.【解】(1)如图①所示.
∵在矩形ABCD中,AB=3,AD=4,
同理可得
在Rt△ADF中,
(2)画图答案不唯一,如图②所示.
由(1)可得AE
∴⊙A的半径r的取值范围为
15.【解】(1)点B,C,D,E在以点M为圆心的同一个圆上,理由如下:
∵BD⊥AC,CE⊥AB,∴∠BEC=∠BDC=90°.
∴点D,E都在以BC为直径的圆上.
又∵M是BC的中点,∴点B,C,D,E在以点M为圆心的同一个圆上.
(2)如图,连接AF并延长交BC于点G,连接BO并延长交⊙O于点H,连接AH,CH.
∵BD,CE是△ABC的高,BD,CE相交于点F,∴AG⊥BC.
∵BH是⊙O的直径,∴∠BAH=∠BCH=90°.∴BA⊥AH,BC⊥CH.∴AG∥CH.
∵CE⊥AB,∴AH∥CE.∴四边形AFCH是平行四边形.∴AH=CF=6.
在Rt△BAH中,AB=8,AH=6,
∴△ABC外接圆的半径长为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
