24.2 点和圆、直线和圆的位置关系 第3课时 切线的判定和性质 同步练习(含答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 第3课时 切线的判定和性质 同步练习(含答案) | 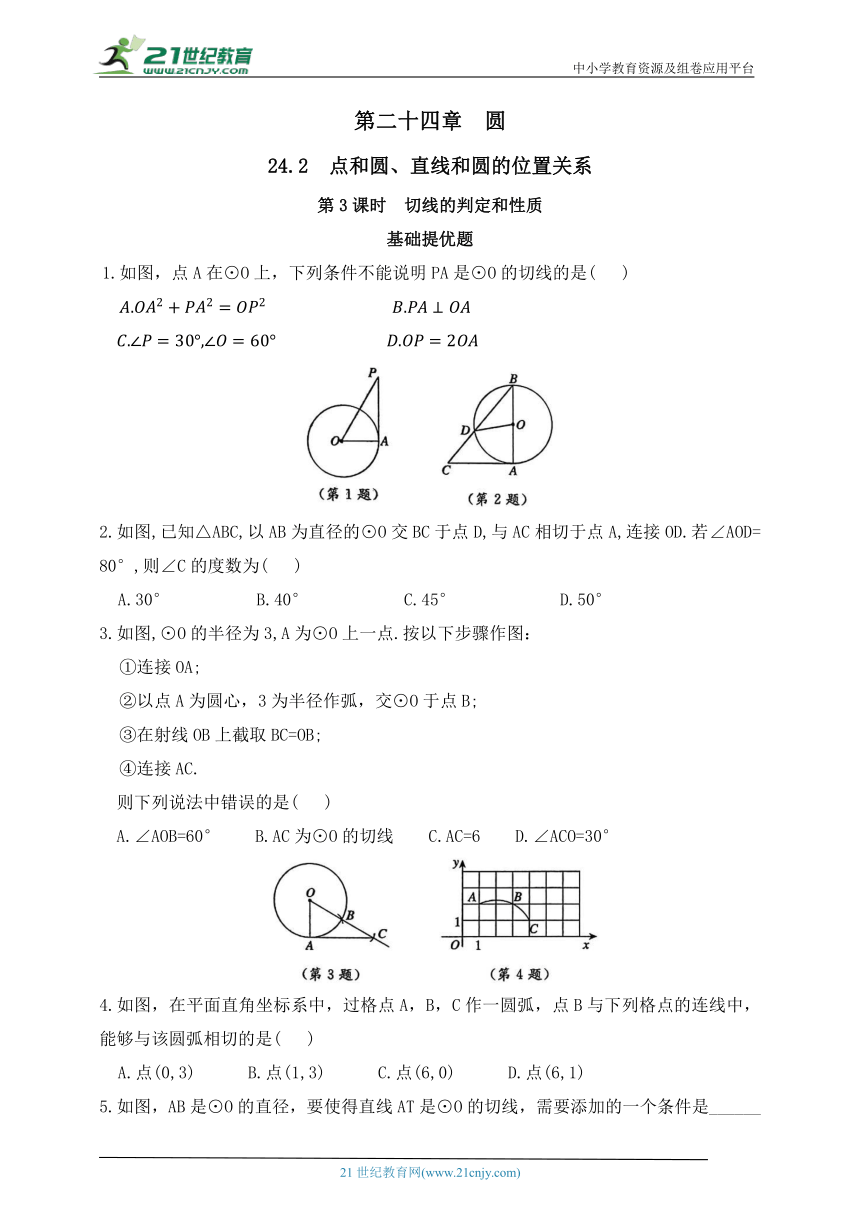 | |
| 格式 | docx | ||
| 文件大小 | 513.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:25:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
第3课时 切线的判定和性质
基础提优题
1.如图,点A在⊙O上,下列条件不能说明PA是⊙O的切线的是( )
2.如图,已知△ABC,以AB为直径的⊙O交BC于点D,与AC相切于点A,连接OD.若∠AOD=80°,则∠C的度数为( )
A.30° B.40° C.45° D.50°
3.如图,⊙O的半径为3,A为⊙O上一点.按以下步骤作图:
①连接OA;
②以点A为圆心,3为半径作弧,交⊙O于点B;
③在射线OB上截取BC=OB;
④连接AC.
则下列说法中错误的是( )
A.∠AOB=60° B.AC为⊙O的切线 C.AC=6 D.∠ACO=30°
4.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
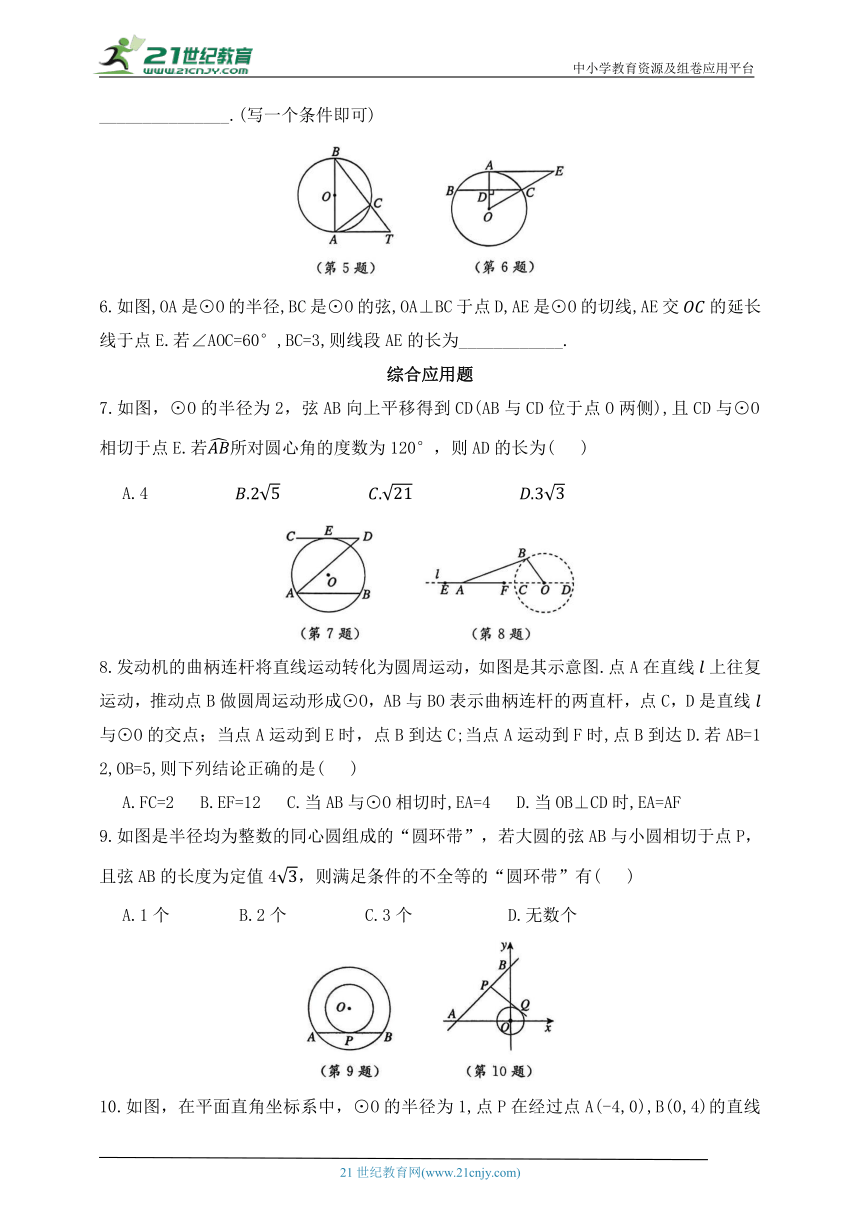
5.如图,AB是⊙O的直径,要使得直线AT是⊙O的切线,需要添加的一个条件是_____________________.(写一个条件即可)
6.如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交的延长线于点E.若∠AOC=60°,BC=3,则线段AE的长为____________.
综合应用题
7.如图,⊙O的半径为2,弦AB向上平移得到CD(AB与CD位于点O两侧),且CD与⊙O相切于点E.若所对圆心角的度数为120°,则AD的长为( )
A.4
8.发动机的曲柄连杆将直线运动转化为圆周运动,如图是其示意图.点A在直线上往复运动,推动点B做圆周运动形成⊙O,AB与BO表示曲柄连杆的两直杆,点C,D是直线与⊙O的交点;当点A运动到E时,点B到达C;当点A运动到F时,点B到达D.若AB=12,OB=5,则下列结论正确的是( )
A.FC=2 B.EF=12 C.当AB与⊙O相切时,EA=4 D.当OB⊥CD时,EA=AF
9.如图是半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值4,则满足条件的不全等的“圆环带”有( )
A.1个 B.2个 C.3个 D.无数个
10.如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0),B(0,4)的直线上,PQ与⊙O相切于点Q,则PQ的最小值为( )
B. C.3
11.如图,△ABC是等腰直角三角形,∠ACB=90°,点O为AB的中点,连接CO交⊙O于点E,⊙O与AC相切于点D.
(1)求证:BC是⊙O的切线;
(2)延长CO交⊙O于点G,连接AG交⊙O于点F,若.求FG的长.
创新拓展题
12.【阅读资料】我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角,如图①中∠PAB所示.同学们研究发现:P为圆上任意一点,若弦AC经过圆心O,且AB切⊙O于点A,此时弦切角∠CAB=∠P(如图②).
证明:∵AB切⊙O于点A,∴∠CAB=90°.
又∵AC是直径,∴∠P=90°,∴∠CAB=∠P.
【问题拓展】若AC不经过圆心O,如图③,当圆心O在∠PCA的内部时,∠CAB=∠P还成立吗 如图④,当圆心O在∠PCA的外部时,∠CAB=∠P还成立吗 请说明理由.
【知识运用】如图⑤,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC相切于点D,与AB,AC分别相交于E,F.求证:EF∥BC.
参考答案
1.D 2.D 3.C 4.B 5.∠TAC=∠B(答案不唯一)
6.3【点拨】连接AB,如图.
∵AE是⊙O的切线,∴半径OA⊥AE.
∵OA⊥CB,∴BC∥AE,∠CDO=90°.
∵∠AOC=60°,
∴∠ABC=∠OCD,∴AB∥CE,
∴四边形ABCE是平行四边形,∴AE=BC=3.
7.C【点拨】如图,连接OA,OB,BD,OE,延长EO交AB于点F,则∠AOB=120°.
∵CD与⊙O相切于点E,∴EF⊥CD.
由平移的性质得CD∥AB,DB⊥AB.∴EF⊥AB.
∴易得四边形BDEF是矩形,AF=BF.∴BD=EF.
∵OA=OB,OF⊥AB,
8.AC【点拨】由题意可得AB=CE=DF=12,AB+BO=OE=17,OC=OB=OD=5.
∴FC=FD-CD=12-5-5=2,故A正确.∴EF=CE-CF=12-2=10,故B错误.
如图①,当AB与⊙O相切时,∠ABO=90°.
∴EA=EO-AO=17-13=4,故C正确.
如图②,当OB⊥CD时,∠AOB=90°.
∴EA≠AF,故D错误.
9.A【点拨】连接OP,OA,如图.
∵大圆的弦AB与小圆相切于点P,
在Rt△OAP中,(
∴(OA-OP)(OA+OP)=12,且OA,OP为整数.
∴或或∴
∴满足条件的不全等的“圆环带”有1个,即大圆半径为4,小圆半径为2.
故选A.
10.B【点拨】连接OP,OQ.
∵PQ是⊙O的切线,∴OQ⊥PQ.
根据勾股定理知
当PO⊥AB时,线段OP最短,则线段PQ最短.
又∵A(-4,0),B(0,4),∴OA=OB=4,
∴PQ的最小值
11.(1)【证明】如图,连接OD,过点O作OP⊥BC于点P.
∵⊙O与AC相切于点D,∴OD⊥AC.
∵△ABC是等腰直角三角形,∠ACB=90°,点O为AB的中点,
∴易得∠OCD=45°,四边形ODCP为矩形.∴CD=DO,OP=CD.
∴OD=OP,即OP是⊙O的半径.∴BC是⊙O的切线.
(2)【解】∵AC=4,△ABC是等腰直角三角形,∠ACB=90°,O是AB的中点,
∴OC=OA=4.
又
如图,连接OF,过点O作OH⊥AG于点H,易得
又
12.【问题拓展】【解】当圆心O在∠PCA的内部时,∠CAB=∠P成立.理由如下:连接AO并延长交⊙O于点D,连接CD,如图①,则∠D=∠P.
∵AD为直径,∴∠ACD=90°,∴∠D+∠CAD=90°.
∵AB切⊙O于点A,∴AD⊥AB,∴∠CAB+∠CAD=90°,∴∠CAB=∠D=∠P.
当圆心O在∠PCA的外部时,∠CAB=∠P成立.理由如下:
连接AO并延长交⊙O于点D',连接PD',如图②,则∠C=∠D',易知∠PAD=∠D',
∴∠PAD=∠C.
又∵∠C+∠CPA+∠PAC=180°,∠PAD+∠PAC+∠CAB=180°,∴∠CAB=∠CPA.
【知识运用】【证明】如图③,连接DF.
∵AD是△ABC中∠BAC的平分线,∴∠BAD=∠CAD.
∵经过点A的⊙O与BC相切于点D,∴∠CDF=∠CAD,∴∠BAD=∠CDF.
∵∠BAD=∠DFE,∴∠CDF=∠DFE,∴EF∥BC.
点归纳 (1)弦切角的定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
(2)弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
第3课时 切线的判定和性质
基础提优题
1.如图,点A在⊙O上,下列条件不能说明PA是⊙O的切线的是( )
2.如图,已知△ABC,以AB为直径的⊙O交BC于点D,与AC相切于点A,连接OD.若∠AOD=80°,则∠C的度数为( )
A.30° B.40° C.45° D.50°
3.如图,⊙O的半径为3,A为⊙O上一点.按以下步骤作图:
①连接OA;
②以点A为圆心,3为半径作弧,交⊙O于点B;
③在射线OB上截取BC=OB;
④连接AC.
则下列说法中错误的是( )
A.∠AOB=60° B.AC为⊙O的切线 C.AC=6 D.∠ACO=30°
4.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
5.如图,AB是⊙O的直径,要使得直线AT是⊙O的切线,需要添加的一个条件是_____________________.(写一个条件即可)
6.如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交的延长线于点E.若∠AOC=60°,BC=3,则线段AE的长为____________.
综合应用题
7.如图,⊙O的半径为2,弦AB向上平移得到CD(AB与CD位于点O两侧),且CD与⊙O相切于点E.若所对圆心角的度数为120°,则AD的长为( )
A.4
8.发动机的曲柄连杆将直线运动转化为圆周运动,如图是其示意图.点A在直线上往复运动,推动点B做圆周运动形成⊙O,AB与BO表示曲柄连杆的两直杆,点C,D是直线与⊙O的交点;当点A运动到E时,点B到达C;当点A运动到F时,点B到达D.若AB=12,OB=5,则下列结论正确的是( )
A.FC=2 B.EF=12 C.当AB与⊙O相切时,EA=4 D.当OB⊥CD时,EA=AF
9.如图是半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值4,则满足条件的不全等的“圆环带”有( )
A.1个 B.2个 C.3个 D.无数个
10.如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-4,0),B(0,4)的直线上,PQ与⊙O相切于点Q,则PQ的最小值为( )
B. C.3
11.如图,△ABC是等腰直角三角形,∠ACB=90°,点O为AB的中点,连接CO交⊙O于点E,⊙O与AC相切于点D.
(1)求证:BC是⊙O的切线;
(2)延长CO交⊙O于点G,连接AG交⊙O于点F,若.求FG的长.
创新拓展题
12.【阅读资料】我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角,如图①中∠PAB所示.同学们研究发现:P为圆上任意一点,若弦AC经过圆心O,且AB切⊙O于点A,此时弦切角∠CAB=∠P(如图②).
证明:∵AB切⊙O于点A,∴∠CAB=90°.
又∵AC是直径,∴∠P=90°,∴∠CAB=∠P.
【问题拓展】若AC不经过圆心O,如图③,当圆心O在∠PCA的内部时,∠CAB=∠P还成立吗 如图④,当圆心O在∠PCA的外部时,∠CAB=∠P还成立吗 请说明理由.
【知识运用】如图⑤,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC相切于点D,与AB,AC分别相交于E,F.求证:EF∥BC.
参考答案
1.D 2.D 3.C 4.B 5.∠TAC=∠B(答案不唯一)
6.3【点拨】连接AB,如图.
∵AE是⊙O的切线,∴半径OA⊥AE.
∵OA⊥CB,∴BC∥AE,∠CDO=90°.
∵∠AOC=60°,
∴∠ABC=∠OCD,∴AB∥CE,
∴四边形ABCE是平行四边形,∴AE=BC=3.
7.C【点拨】如图,连接OA,OB,BD,OE,延长EO交AB于点F,则∠AOB=120°.
∵CD与⊙O相切于点E,∴EF⊥CD.
由平移的性质得CD∥AB,DB⊥AB.∴EF⊥AB.
∴易得四边形BDEF是矩形,AF=BF.∴BD=EF.
∵OA=OB,OF⊥AB,
8.AC【点拨】由题意可得AB=CE=DF=12,AB+BO=OE=17,OC=OB=OD=5.
∴FC=FD-CD=12-5-5=2,故A正确.∴EF=CE-CF=12-2=10,故B错误.
如图①,当AB与⊙O相切时,∠ABO=90°.
∴EA=EO-AO=17-13=4,故C正确.
如图②,当OB⊥CD时,∠AOB=90°.
∴EA≠AF,故D错误.
9.A【点拨】连接OP,OA,如图.
∵大圆的弦AB与小圆相切于点P,
在Rt△OAP中,(
∴(OA-OP)(OA+OP)=12,且OA,OP为整数.
∴或或∴
∴满足条件的不全等的“圆环带”有1个,即大圆半径为4,小圆半径为2.
故选A.
10.B【点拨】连接OP,OQ.
∵PQ是⊙O的切线,∴OQ⊥PQ.
根据勾股定理知
当PO⊥AB时,线段OP最短,则线段PQ最短.
又∵A(-4,0),B(0,4),∴OA=OB=4,
∴PQ的最小值
11.(1)【证明】如图,连接OD,过点O作OP⊥BC于点P.
∵⊙O与AC相切于点D,∴OD⊥AC.
∵△ABC是等腰直角三角形,∠ACB=90°,点O为AB的中点,
∴易得∠OCD=45°,四边形ODCP为矩形.∴CD=DO,OP=CD.
∴OD=OP,即OP是⊙O的半径.∴BC是⊙O的切线.
(2)【解】∵AC=4,△ABC是等腰直角三角形,∠ACB=90°,O是AB的中点,
∴OC=OA=4.
又
如图,连接OF,过点O作OH⊥AG于点H,易得
又
12.【问题拓展】【解】当圆心O在∠PCA的内部时,∠CAB=∠P成立.理由如下:连接AO并延长交⊙O于点D,连接CD,如图①,则∠D=∠P.
∵AD为直径,∴∠ACD=90°,∴∠D+∠CAD=90°.
∵AB切⊙O于点A,∴AD⊥AB,∴∠CAB+∠CAD=90°,∴∠CAB=∠D=∠P.
当圆心O在∠PCA的外部时,∠CAB=∠P成立.理由如下:
连接AO并延长交⊙O于点D',连接PD',如图②,则∠C=∠D',易知∠PAD=∠D',
∴∠PAD=∠C.
又∵∠C+∠CPA+∠PAC=180°,∠PAD+∠PAC+∠CAB=180°,∴∠CAB=∠CPA.
【知识运用】【证明】如图③,连接DF.
∵AD是△ABC中∠BAC的平分线,∴∠BAD=∠CAD.
∵经过点A的⊙O与BC相切于点D,∴∠CDF=∠CAD,∴∠BAD=∠CDF.
∵∠BAD=∠DFE,∴∠CDF=∠DFE,∴EF∥BC.
点归纳 (1)弦切角的定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
(2)弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
