24.2 点和圆、直线和圆的位置关系 第4课时 切线长定理和三角形的内切圆 同步练习(含答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 第4课时 切线长定理和三角形的内切圆 同步练习(含答案) | 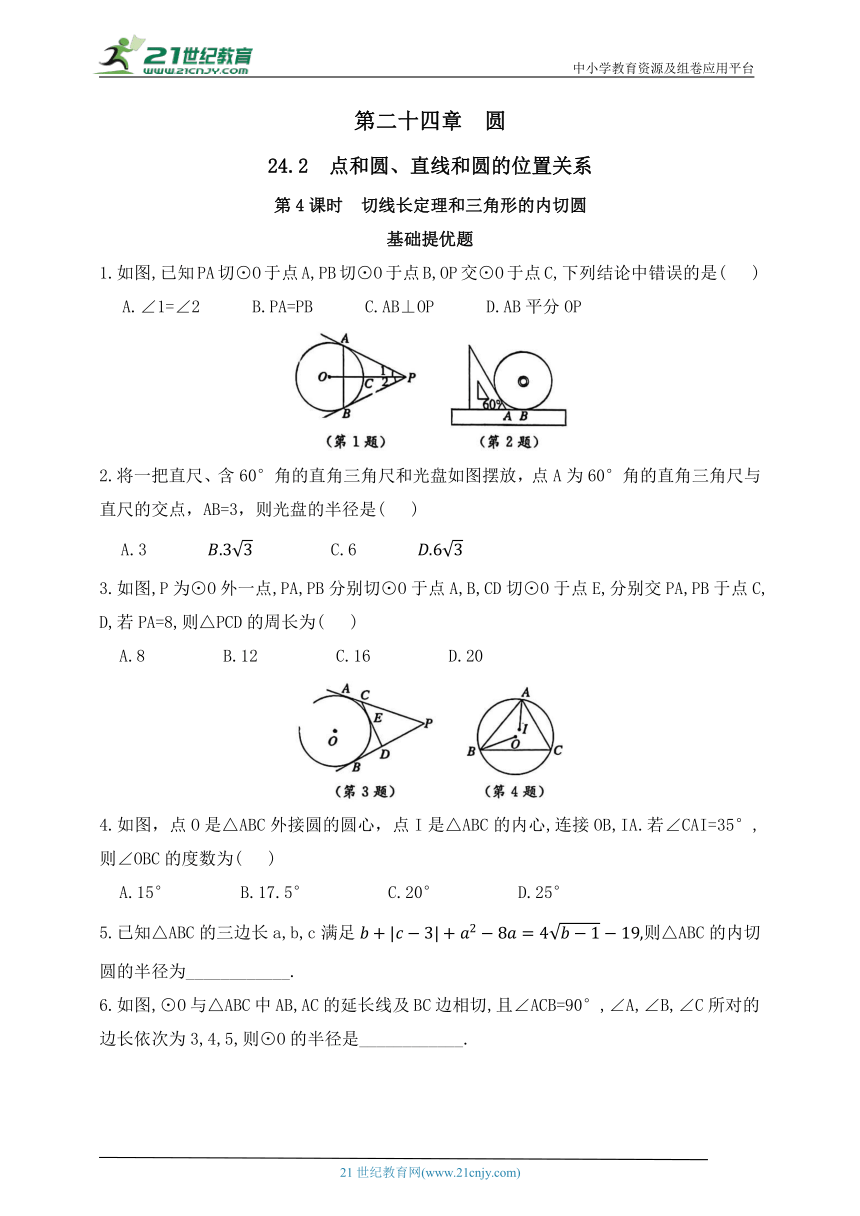 | |
| 格式 | docx | ||
| 文件大小 | 450.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:25:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
第4课时 切线长定理和三角形的内切圆
基础提优题
1.如图,已知PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.AB平分OP
2.将一把直尺、含60°角的直角三角尺和光盘如图摆放,点A为60°角的直角三角尺与直尺的交点,AB=3,则光盘的半径是( )
A.3 C.6
3.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,分别交PA,PB于点C,D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
4.如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为( )
A.15° B.17.5° C.20° D.25°
5.已知△ABC的三边长a,b,c满足则△ABC的内切圆的半径为____________.
6.如图,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是____________.
综合应用题
7.如图,⊙O为四边形ABCD的内切圆,∠A=∠B=90°,AD=4,BC=6,则⊙O的半径为( )
A.2 B. C. D.3
8.如图,点O是△AEF的内心,过点O作BC∥EF分别交AE,AF于点B,C,已知△AEF的周长为8,EF=x,△ABC的周长为y,则表示y与x的函数图象大致是( )
9.如图,平面直角坐标系中三个点的坐标为A(1,1),B(2,4),C(3,1).则△ABC的内切圆半径长为______________.
10.如图,把Rt△OAB置于平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),点P是Rt△OAB内切圆的圆心,将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第1次滚动后圆心为P ,第2次滚动后圆心为P ,…,以此规律递推,第2025次后,Rt△OAB内切圆的圆心P 的坐标为___________.
11.如图,点B的坐标为(2,0),以O点为圆心,以OB长为半径的圆交y轴于点A,点C为第一象限圆上一动点,CD⊥x轴于D点,点I为△OCD的内心,则AI的最小值为_____________.
12.如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形;
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
创新拓展题
13.使用“面积法”解决下列问题:
(1)若Rt△ABC两条直角边长分别为3和4,则它的内切圆半径为;
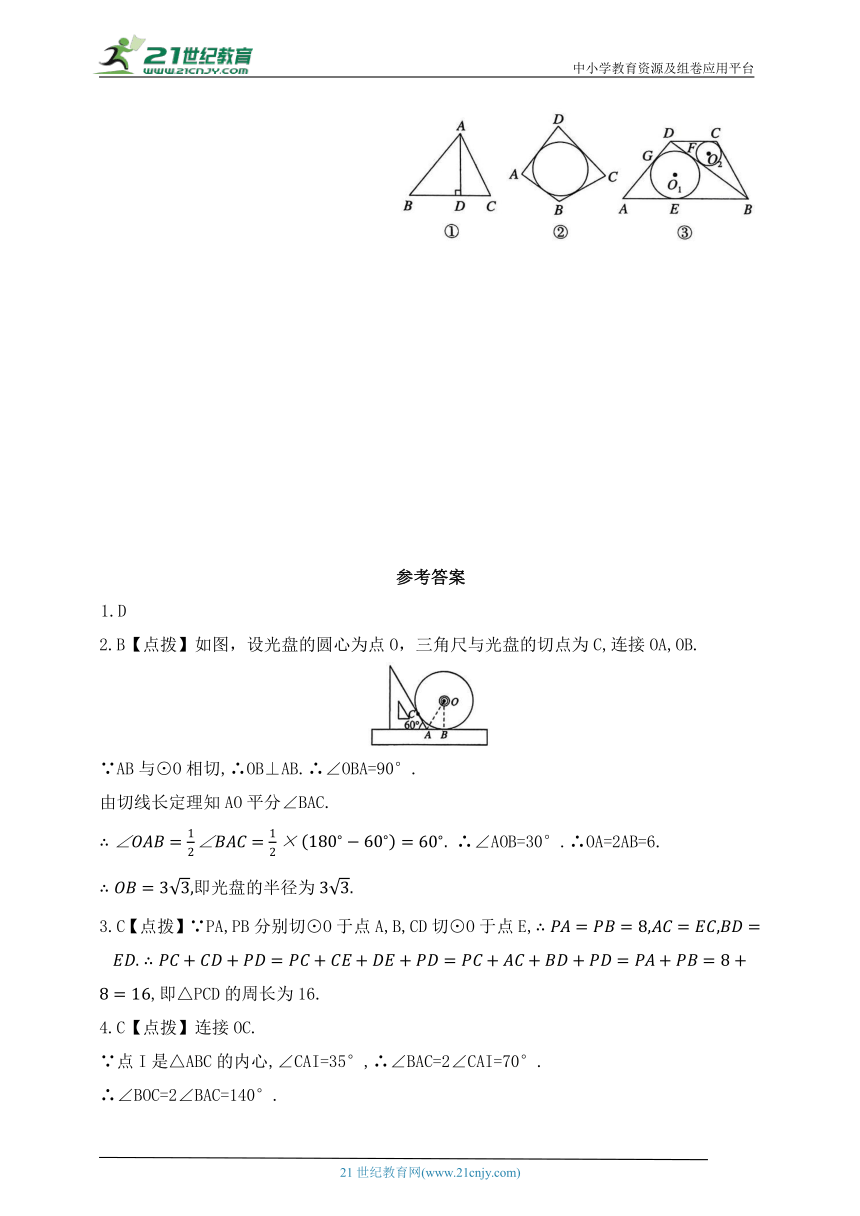
(2)如图①,在△ABC中,AB=15,BC=14,AC=13,AD是BC边上的高,求AD长及△ABC的内切圆半径;
(3)若△ABC的周长为,面积为S,内切圆⊙O的半径为r,直接写出r与S,之间的关系;
(4)若四边形ABCD存在内切圆(与各边都相切的圆),如图②,且四边形ABCD的面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(5)如图③,在四边形ABCD中,半径为r 的⊙O 与半径为r 的⊙O 分别为与的内切圆,⊙O 与△ABD分别相切于点E,F,G,若求r 的值.
参考答案
1.D
2.B【点拨】如图,设光盘的圆心为点O,三角尺与光盘的切点为C,连接OA,OB.
∵AB与⊙O相切,∴OB⊥AB.∴∠OBA=90°.
由切线长定理知AO平分∠BAC.
∴∠AOB=30°.∴OA=2AB=6.
即光盘的半径为
3.C【点拨】∵PA,PB分别切⊙O于点A,B,CD切⊙O于点E,,即△PCD的周长为16.
4.C【点拨】连接OC.
∵点I是△ABC的内心,∠CAI=35°,∴∠BAC=2∠CAI=70°.
∴∠BOC=2∠BAC=140°.
∵OB=OC,
点易错 本题易因混淆内心与外心的概念而致错.
5.1【点拨】,∴.
∵3 +4 =25=C是直角三角形.
设△ABC内切圆的半径为r.
根据题意,得解得r=1.
6.2【点拨】如图,令AB,AC的延长线及BC与⊙O的切点分别为F,D,E,连接OD,OE.
∵⊙O与AF,AD,BC都相切,∴AF=AD,BE=BF,CE=CD,OD⊥AD,OE⊥BC.
∵∠ACB=90°,∴∠ECD=90°.又∵OE=OD,∴四边形ODCE是正方形.
设OD=r,则CD=CE=r.
∵BC=3,∴BE=BF=3-r.
∵AB=5,AC=4,∴AF=AB+BF=5+3-r,AD=AC+CD=4+r.
∴5+3-r=4+r,解得r=2,即⊙O的半径是2.
7.B【点拨】如图,过点D作DG⊥BC于点G,设AD,DC,BC,AB与⊙O的切点分别是H,F,E,M,连接OM,OE,OH,则OM⊥AB,OH⊥AD,OE⊥BC.
易知H,O,E三点共线.
∵∠A=∠B=90°,∴易知四边形AMOH,四边形BMOE都是正方形,四边形HEGD,四边形ABGD都是矩形.∴AH=OM=BE,HE=DG,BG=AD=4.∴CG=BC-BG=6-4=2.
由切线长定理得DF=DH,CF=CE.
设⊙O的半径为R,则BE=AH=OM=R,DG=HE=2R.∴CF=CE=6-R,DF=DH=4-R.
解得即⊙O的半径为
8.A【点拨】连接EO,FO.∵点O是△AEF的内心,∴∠BEO=∠OEF,∠OFC=∠OFE.
∵BC∥EF,∴∠BOE=∠OEF,∠COF=∠OFE,∴∠BOE=∠BEO,∠COF=∠OFC,
∴BO=BE,CO=CF,∴△ABC的周长=AB+BO+OC+AC=AB+BE+CF+AC=AE+AF.
∵△AEF的周长为8,EF=x,∴y=8-x.
∵AE+AF>EF,∴y>x.∴8-x>x.∴0∴y与x的函数关系式为y=-x+8(0【点拨】如图,设△ABC的内切圆⊙I与AB,BC,AC分别相切于点F,J,E,连接IF,IJ,IE,BI.
∵A(1,1),B(2,4),C(3,1),∴AB=CB.
∵点I为△ABC的内切圆的圆心,∴BI平分∠ABC.
∵AB=CB,∴BI在AC的垂直平分线上,
∵IE⊥AC,∴B,I,E在同一直线上,∴E(2,1),∴BE=4-1=3.
连接AI,CI,设△ABC的内切圆的半径长为r.
解得
10.(8101,1)【点拨】∵点A的坐标为(0,4),点B的坐标为(3,0),∴OA=4,OB=3,∴.易得Rt△OAB内切圆的半径为
点P的坐标为(1,1).
∵将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第1次滚动后圆心为P ,第2次滚动后圆心为P ,…,∴P (3+5+4+1,1),即(13,1),每.滚动3次为一个循环.∵2025÷3=675,∴第2025次滚动后,Rt△OAB内切圆的圆心P 的横坐标是675×(3+5+4)+1,即P 的横坐标是8101,
∴P 的坐标为(8101,1).
【点拨】如图,连接OI,IB,作△OIB的外接圆,圆心为P,连接PO,PB,IC,ON,BN.
∵点I为△OCD的内心,∴∠IOC=∠IOB.
在△IOC和△IOB中,∴△IOC≌△IOB(SAS),∴∠OIC=∠OIB.
∵CD⊥x轴,∴∠ODC=90°,∴∠COD+∠OCD=90°,
∴∠OIC=135°,∴∠OIB=135°,∴∠ONB=45°,∴∠OPB=90°.
∵点B的坐标为(2,0),∴OB=2,∴OA=2,易得
∴A(0,2),P(1,-1),当A,I,P三点共线时,AI取得最小值,此时AI=AP-PI=
12.(1)【解】∵AD是边BC上的中线,
∵CE∥AD,∴AD为△BCE的中位线,∴CE=2AD=6.
(2)【证明】∵CE∥AD,∴∠BAD=∠E,∠CAD=∠ACE.
∵∠BAD=∠CAD,∴∠ACE=∠E,∴AE=AC.
由(1)知AD为△BCE的中位线,∴AB=AE,∴AB=AC,∴△ABC为等腰三角形.
(3)【解】如图,连接BP,BQ,CP,CQ,易得∠ADB=∠BDP=90°,
∴在Rt△ABD中,
设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中,PD=R-3,PB=R,BD=4,
∴(R-3) +4 =R ,解得
解得即
C.的外接圆圆心P与内切圆圆心Q之间的距离为
13.【解】(1)1
(2)设BD=x,则CD=14-x,设△ABC的内切圆半径为r,在Rt△ABD中,在Rt△ACD中,解得x=9,则
(4)设四边形ABCD内切圆的圆心为O,半径为r,连接OA,OB,OC,OD,则
(CD=20,∴BD=16.∵⊙O是△ABD的内切圆,∴AE=AG=8,BE=BF,DF=DG,∴DG+BE=BD=16,
∴设DG=x,则BE=16-x.∵∠ADB=90°,
∴AD +BD =AB ,即(解得x=4,
∴AD=16=96.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
第4课时 切线长定理和三角形的内切圆
基础提优题
1.如图,已知PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中错误的是( )
A.∠1=∠2 B.PA=PB C.AB⊥OP D.AB平分OP
2.将一把直尺、含60°角的直角三角尺和光盘如图摆放,点A为60°角的直角三角尺与直尺的交点,AB=3,则光盘的半径是( )
A.3 C.6
3.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,分别交PA,PB于点C,D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
4.如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为( )
A.15° B.17.5° C.20° D.25°
5.已知△ABC的三边长a,b,c满足则△ABC的内切圆的半径为____________.
6.如图,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是____________.
综合应用题
7.如图,⊙O为四边形ABCD的内切圆,∠A=∠B=90°,AD=4,BC=6,则⊙O的半径为( )
A.2 B. C. D.3
8.如图,点O是△AEF的内心,过点O作BC∥EF分别交AE,AF于点B,C,已知△AEF的周长为8,EF=x,△ABC的周长为y,则表示y与x的函数图象大致是( )
9.如图,平面直角坐标系中三个点的坐标为A(1,1),B(2,4),C(3,1).则△ABC的内切圆半径长为______________.
10.如图,把Rt△OAB置于平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),点P是Rt△OAB内切圆的圆心,将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第1次滚动后圆心为P ,第2次滚动后圆心为P ,…,以此规律递推,第2025次后,Rt△OAB内切圆的圆心P 的坐标为___________.
11.如图,点B的坐标为(2,0),以O点为圆心,以OB长为半径的圆交y轴于点A,点C为第一象限圆上一动点,CD⊥x轴于D点,点I为△OCD的内心,则AI的最小值为_____________.
12.如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形;
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
创新拓展题
13.使用“面积法”解决下列问题:
(1)若Rt△ABC两条直角边长分别为3和4,则它的内切圆半径为;
(2)如图①,在△ABC中,AB=15,BC=14,AC=13,AD是BC边上的高,求AD长及△ABC的内切圆半径;
(3)若△ABC的周长为,面积为S,内切圆⊙O的半径为r,直接写出r与S,之间的关系;
(4)若四边形ABCD存在内切圆(与各边都相切的圆),如图②,且四边形ABCD的面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(5)如图③,在四边形ABCD中,半径为r 的⊙O 与半径为r 的⊙O 分别为与的内切圆,⊙O 与△ABD分别相切于点E,F,G,若求r 的值.
参考答案
1.D
2.B【点拨】如图,设光盘的圆心为点O,三角尺与光盘的切点为C,连接OA,OB.
∵AB与⊙O相切,∴OB⊥AB.∴∠OBA=90°.
由切线长定理知AO平分∠BAC.
∴∠AOB=30°.∴OA=2AB=6.
即光盘的半径为
3.C【点拨】∵PA,PB分别切⊙O于点A,B,CD切⊙O于点E,,即△PCD的周长为16.
4.C【点拨】连接OC.
∵点I是△ABC的内心,∠CAI=35°,∴∠BAC=2∠CAI=70°.
∴∠BOC=2∠BAC=140°.
∵OB=OC,
点易错 本题易因混淆内心与外心的概念而致错.
5.1【点拨】,∴.
∵3 +4 =25=C是直角三角形.
设△ABC内切圆的半径为r.
根据题意,得解得r=1.
6.2【点拨】如图,令AB,AC的延长线及BC与⊙O的切点分别为F,D,E,连接OD,OE.
∵⊙O与AF,AD,BC都相切,∴AF=AD,BE=BF,CE=CD,OD⊥AD,OE⊥BC.
∵∠ACB=90°,∴∠ECD=90°.又∵OE=OD,∴四边形ODCE是正方形.
设OD=r,则CD=CE=r.
∵BC=3,∴BE=BF=3-r.
∵AB=5,AC=4,∴AF=AB+BF=5+3-r,AD=AC+CD=4+r.
∴5+3-r=4+r,解得r=2,即⊙O的半径是2.
7.B【点拨】如图,过点D作DG⊥BC于点G,设AD,DC,BC,AB与⊙O的切点分别是H,F,E,M,连接OM,OE,OH,则OM⊥AB,OH⊥AD,OE⊥BC.
易知H,O,E三点共线.
∵∠A=∠B=90°,∴易知四边形AMOH,四边形BMOE都是正方形,四边形HEGD,四边形ABGD都是矩形.∴AH=OM=BE,HE=DG,BG=AD=4.∴CG=BC-BG=6-4=2.
由切线长定理得DF=DH,CF=CE.
设⊙O的半径为R,则BE=AH=OM=R,DG=HE=2R.∴CF=CE=6-R,DF=DH=4-R.
解得即⊙O的半径为
8.A【点拨】连接EO,FO.∵点O是△AEF的内心,∴∠BEO=∠OEF,∠OFC=∠OFE.
∵BC∥EF,∴∠BOE=∠OEF,∠COF=∠OFE,∴∠BOE=∠BEO,∠COF=∠OFC,
∴BO=BE,CO=CF,∴△ABC的周长=AB+BO+OC+AC=AB+BE+CF+AC=AE+AF.
∵△AEF的周长为8,EF=x,∴y=8-x.
∵AE+AF>EF,∴y>x.∴8-x>x.∴0
∵A(1,1),B(2,4),C(3,1),∴AB=CB.
∵点I为△ABC的内切圆的圆心,∴BI平分∠ABC.
∵AB=CB,∴BI在AC的垂直平分线上,
∵IE⊥AC,∴B,I,E在同一直线上,∴E(2,1),∴BE=4-1=3.
连接AI,CI,设△ABC的内切圆的半径长为r.
解得
10.(8101,1)【点拨】∵点A的坐标为(0,4),点B的坐标为(3,0),∴OA=4,OB=3,∴.易得Rt△OAB内切圆的半径为
点P的坐标为(1,1).
∵将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第1次滚动后圆心为P ,第2次滚动后圆心为P ,…,∴P (3+5+4+1,1),即(13,1),每.滚动3次为一个循环.∵2025÷3=675,∴第2025次滚动后,Rt△OAB内切圆的圆心P 的横坐标是675×(3+5+4)+1,即P 的横坐标是8101,
∴P 的坐标为(8101,1).
【点拨】如图,连接OI,IB,作△OIB的外接圆,圆心为P,连接PO,PB,IC,ON,BN.
∵点I为△OCD的内心,∴∠IOC=∠IOB.
在△IOC和△IOB中,∴△IOC≌△IOB(SAS),∴∠OIC=∠OIB.
∵CD⊥x轴,∴∠ODC=90°,∴∠COD+∠OCD=90°,
∴∠OIC=135°,∴∠OIB=135°,∴∠ONB=45°,∴∠OPB=90°.
∵点B的坐标为(2,0),∴OB=2,∴OA=2,易得
∴A(0,2),P(1,-1),当A,I,P三点共线时,AI取得最小值,此时AI=AP-PI=
12.(1)【解】∵AD是边BC上的中线,
∵CE∥AD,∴AD为△BCE的中位线,∴CE=2AD=6.
(2)【证明】∵CE∥AD,∴∠BAD=∠E,∠CAD=∠ACE.
∵∠BAD=∠CAD,∴∠ACE=∠E,∴AE=AC.
由(1)知AD为△BCE的中位线,∴AB=AE,∴AB=AC,∴△ABC为等腰三角形.
(3)【解】如图,连接BP,BQ,CP,CQ,易得∠ADB=∠BDP=90°,
∴在Rt△ABD中,
设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中,PD=R-3,PB=R,BD=4,
∴(R-3) +4 =R ,解得
解得即
C.的外接圆圆心P与内切圆圆心Q之间的距离为
13.【解】(1)1
(2)设BD=x,则CD=14-x,设△ABC的内切圆半径为r,在Rt△ABD中,在Rt△ACD中,解得x=9,则
(4)设四边形ABCD内切圆的圆心为O,半径为r,连接OA,OB,OC,OD,则
(CD=20,∴BD=16.∵⊙O是△ABD的内切圆,∴AE=AG=8,BE=BF,DF=DG,∴DG+BE=BD=16,
∴设DG=x,则BE=16-x.∵∠ADB=90°,
∴AD +BD =AB ,即(解得x=4,
∴AD=16=96.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
