24.3 正多边形和圆 同步练习(含答案)
文档属性
| 名称 | 24.3 正多边形和圆 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:26:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.3 正多边形和圆
基础提优题
1.下列叙述中,正确的有( )
①正多边形和圆既是轴对称图形又是中心对称图形:
②各边相等的多边形各角也相等;
③正多边形的中心与其内切圆圆心重合;
④正多边形的一边所对的中心角与它的一个外角相等.
A.1个 B.2个 C.3个 D.4个
2.苯分子的环状结构是由德国化学家凯库勒提出的,随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面,且所有碳碳键的键长都相等(如图①),组成了一个完美的六边形(正六边形),图②是其平面示意图,则∠1的度数为( )
A.130° B.120° C.110° D.60°
3.已知,正六边形ABCDEF的面积为6,则正六边形的边长为( )
A.1 B. C.2 D.4
4.如图,△ADF是⊙O的内接正三角形,四边形ACEG是⊙O的内接正方形,六边形AB-DEFH是⊙O的内接正六边形,设上述正三角形的周长为C 、正方形的周长为C ,正六边形的周长为C ,则C :C :C 为( )
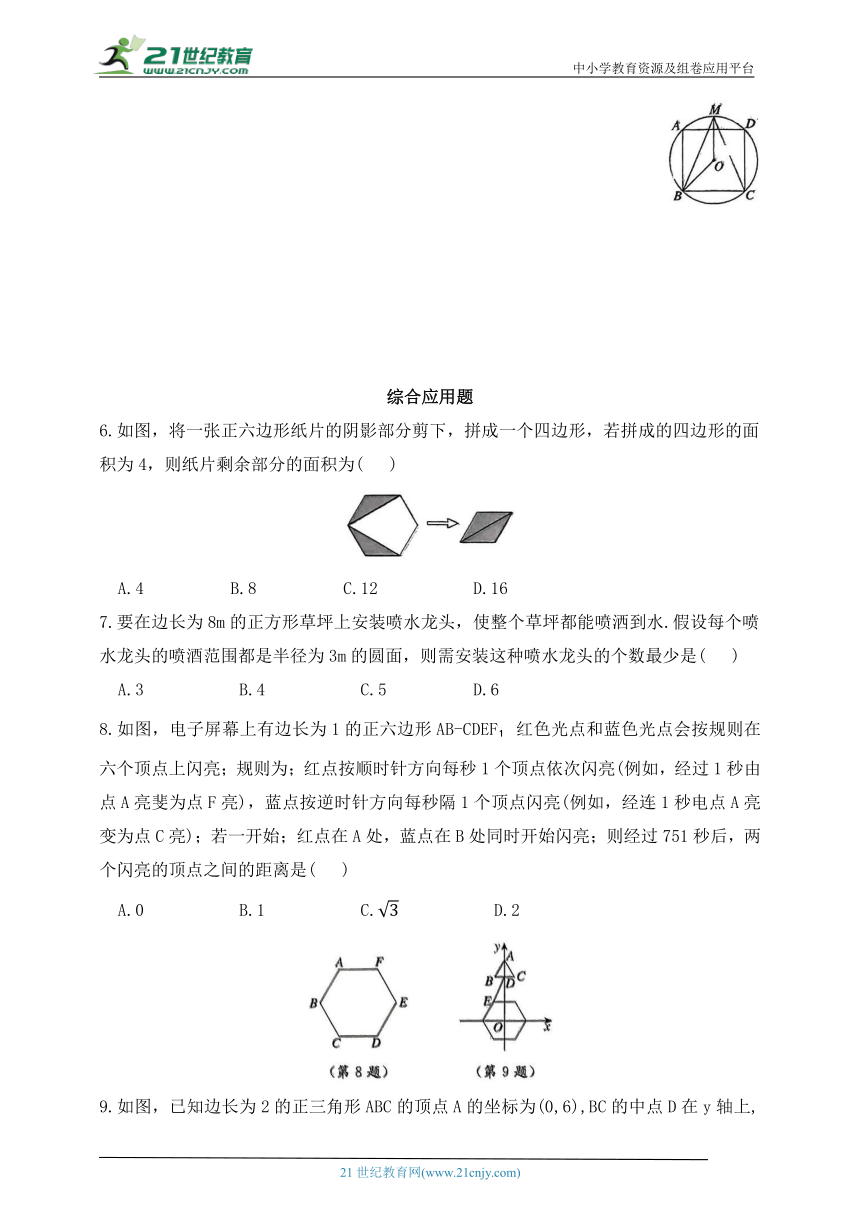
5.如图,正方形ABCD内接于⊙O,M为弧AD的中点,连接BM,CM,OB,OM.
(1)求证:BM=CM;
(2)求∠BOM的度数.
综合应用题
6.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为4,则纸片剩余部分的面积为( )
A.4 B.8 C.12 D.16
7.要在边长为8m的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷酒范围都是半径为3m的圆面,则需安装这种喷水龙头的个数最少是( )
A.3 B.4 C.5 D.6
8.如图,电子屏幕上有边长为1的正六边形AB-CDEF 红色光点和蓝色光点会按规则在六个顶点上闪亮;规则为;红点按顺时针方向每秒1个顶点依次闪亮(例如,经过1秒由点A亮斐为点F亮),蓝点按逆时针方向每秒隔1个顶点闪亮(例如,经连1秒电点A亮变为点C亮);若一开始;红点在A处,蓝点在B处同时开始闪亮;则经过751秒后,两个闪亮的顶点之间的距离是( )
A.0 B.1 C. D.2
9.如图,已知边长为2的正三角形ABC的顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
A.3 C.4
10.如图①,正五边形ABCDE内接于⊙O,阅读以下作图过程,并回答下列问题:
作法:1.作直径AF;2.以F为圆心,FO长为半径作圆弧,与⊙O交于点M,N;3.连接AM,MN,NA.如图②.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在⊙O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
创新拓展题
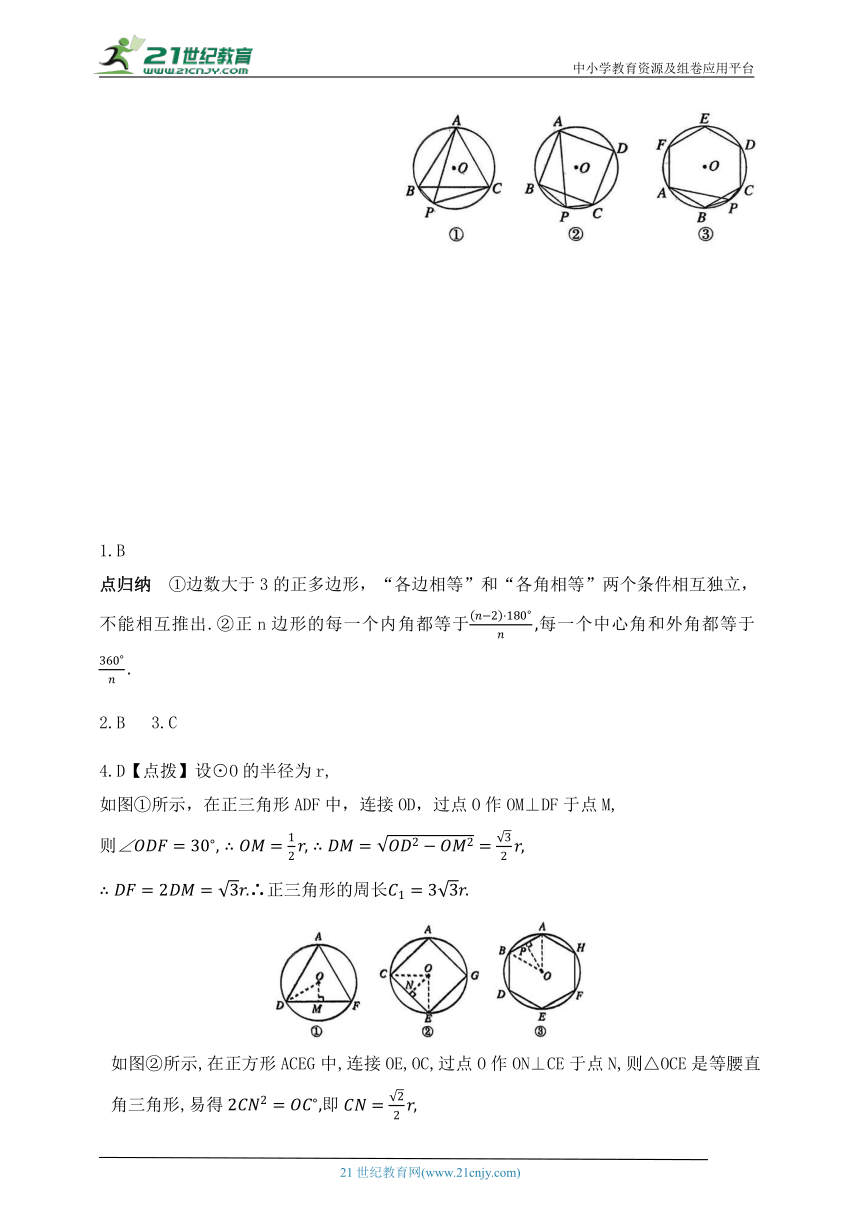
11.(1)如图①,已知△ABC是⊙O的内接正三角形,点P为上一动点,求证:
PA=PB+PC;
(2)如图②,四边形ABCD是⊙O的内接正方形,点P为BC上一动点,求证:
(3)如图③,六边形ABCDEF是⊙O的内接正六边形,点P为上一动点,请探究PA,PB,PC三者之间有何数量关系,并予以证明.
1.B
点归纳 ①边数大于3的正多边形,“各边相等”和“各角相等”两个条件相互独立,不能相互推出.②正n边形的每一个内角都等于每一个中心角和外角都等于
2.B 3.C
4.D【点拨】设⊙O的半径为r,
如图①所示,在正三角形ADF中,连接OD,过点O作OM⊥DF于点M,
则
∴正三角形的周长
如图②所示,在正方形ACEG中,连接OE,OC,过点O作ON⊥CE于点N,则△OCE是等腰直角三角形,易得即
∴正方形的周长
如图③所示,在正六边形ABDEFH中,连接OA,OB,过点O作OP⊥AB于点P,则△OAB是等边三角形,∴正六边形的周长
5.(1)【证明】∵四边形ABCD是正方形,
∵M为AD的中点,
(2)【解】连接OA,如图.
∵四边形ABCD是正方形,∴∠AOB=90°.
∵M为弧AD的中点,∴∠AOM=45°.∴∠BOM=∠AOB+∠AOM=135°.
6.B【点拨】如图,将正六边形分为6个全等的三角形.
∵拼成的四边形的面积为4,∴每一个三角形的面积为2.
∵剩余部分可分割为4个三角形,∴剩余部分的面积为8.
7.B【点拨】∵正方形草坪的边长为8m,∴正方形草坪的外接圆的半径是则其外接圆的面积是∵每个喷水龙头喷洒的面积是3 ×π=9π(m ),∴32π÷9π=4(个).
8.C【点拨】∵红点每6秒闪亮的顶点会转动1周,而751÷6=125……1,
∴经过751秒后,红点闪到了点F处.
∵蓝点每3秒闪亮的顶点会转动1周,而751÷3=250……1,
∴经过751秒后,蓝点闪到了点D处.
连接FD,过点E作EH⊥FD于点H,如图.
∵“六边形ABCDEF是正六边形,∴∠DEF=120°,EF=ED.∴∠EFH=30°,FD=2FH.
即经过751秒后,两个闪亮的顶点之间的距离是
9.B【点拨】如图,连接OE,
根据DE≥OD-OE,可知当D,E,O三点共线,即点E位于点E'处时,DE最小.
∵边长为2的△ABC是等边三角形,点A的坐标为(0,6),BC的中点D在y轴上,
∴AD⊥BC,OA=6,BD=CD=BC=1.
∵正六边形的边长为2,∴EF=2,∠EOF=60°,OE=OF.∴△EOF是等边三角形.
即DE的最小值为
10.【解】(1)∵五边形ABCDE是正五边形,
(2)△AMN是正三角形.
理由如下:连接ON,NF,如图.
由题意可得FN=OF=ON,∴△FON是正三角形.∴∠NFA=60°.∴∠NMA=60°.
同理可得∠ANM=60°,∴△AMN是正三角形.
(3)如图,连接OD.∵∠AMN=60°,∴∠AON=120°.
∴∠NOD=∠AOD-∠AON=144°-120°=24°.
∴n的值是15.
11.(1)【证明】如图①,延长BP至E,使PE=PC,连接CE.
∵A,B,P,C四点共圆,∴∠BAC+∠BPC=180°.
∵∠BPC+∠EPC=180°,∴∠CPE=∠BAC=60°.
又∵PE=PC,∴△PCE是正三角形,∴CE=PC,∠PCE=60°.
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP.
∵△ABC,△PCE都为正三角形,∴CE=PC,AC=BC,
∴△ECB≌△PCA(SAS),∴PA=BE=PB+PE=PB+PC.
(2)【证明】如图②,连接OA,OB,过点B作BE⊥PB交PA于点E.
∵∠1+∠2=∠2+∠3=90°,∴∠1=∠3.
又∵AB=BC,∴△ABE≌△CBP,∴PC=AE.
(3)【解】证明如下:如图③,过点B作BM⊥AP于点M,在AP上截取AQ=CP,连接BQ.
∵∠BAP=∠BCP,AB=BC,AQ=CP,∴△ABQ≌△CBP.∴BQ=BP.∴MP=QM.
易得∠APB=30°,∴BM=PB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.3 正多边形和圆
基础提优题
1.下列叙述中,正确的有( )
①正多边形和圆既是轴对称图形又是中心对称图形:
②各边相等的多边形各角也相等;
③正多边形的中心与其内切圆圆心重合;
④正多边形的一边所对的中心角与它的一个外角相等.
A.1个 B.2个 C.3个 D.4个
2.苯分子的环状结构是由德国化学家凯库勒提出的,随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面,且所有碳碳键的键长都相等(如图①),组成了一个完美的六边形(正六边形),图②是其平面示意图,则∠1的度数为( )
A.130° B.120° C.110° D.60°
3.已知,正六边形ABCDEF的面积为6,则正六边形的边长为( )
A.1 B. C.2 D.4
4.如图,△ADF是⊙O的内接正三角形,四边形ACEG是⊙O的内接正方形,六边形AB-DEFH是⊙O的内接正六边形,设上述正三角形的周长为C 、正方形的周长为C ,正六边形的周长为C ,则C :C :C 为( )
5.如图,正方形ABCD内接于⊙O,M为弧AD的中点,连接BM,CM,OB,OM.
(1)求证:BM=CM;
(2)求∠BOM的度数.
综合应用题
6.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为4,则纸片剩余部分的面积为( )
A.4 B.8 C.12 D.16
7.要在边长为8m的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷酒范围都是半径为3m的圆面,则需安装这种喷水龙头的个数最少是( )
A.3 B.4 C.5 D.6
8.如图,电子屏幕上有边长为1的正六边形AB-CDEF 红色光点和蓝色光点会按规则在六个顶点上闪亮;规则为;红点按顺时针方向每秒1个顶点依次闪亮(例如,经过1秒由点A亮斐为点F亮),蓝点按逆时针方向每秒隔1个顶点闪亮(例如,经连1秒电点A亮变为点C亮);若一开始;红点在A处,蓝点在B处同时开始闪亮;则经过751秒后,两个闪亮的顶点之间的距离是( )
A.0 B.1 C. D.2
9.如图,已知边长为2的正三角形ABC的顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
A.3 C.4
10.如图①,正五边形ABCDE内接于⊙O,阅读以下作图过程,并回答下列问题:
作法:1.作直径AF;2.以F为圆心,FO长为半径作圆弧,与⊙O交于点M,N;3.连接AM,MN,NA.如图②.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN长为半径,在⊙O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
创新拓展题
11.(1)如图①,已知△ABC是⊙O的内接正三角形,点P为上一动点,求证:
PA=PB+PC;
(2)如图②,四边形ABCD是⊙O的内接正方形,点P为BC上一动点,求证:
(3)如图③,六边形ABCDEF是⊙O的内接正六边形,点P为上一动点,请探究PA,PB,PC三者之间有何数量关系,并予以证明.
1.B
点归纳 ①边数大于3的正多边形,“各边相等”和“各角相等”两个条件相互独立,不能相互推出.②正n边形的每一个内角都等于每一个中心角和外角都等于
2.B 3.C
4.D【点拨】设⊙O的半径为r,
如图①所示,在正三角形ADF中,连接OD,过点O作OM⊥DF于点M,
则
∴正三角形的周长
如图②所示,在正方形ACEG中,连接OE,OC,过点O作ON⊥CE于点N,则△OCE是等腰直角三角形,易得即
∴正方形的周长
如图③所示,在正六边形ABDEFH中,连接OA,OB,过点O作OP⊥AB于点P,则△OAB是等边三角形,∴正六边形的周长
5.(1)【证明】∵四边形ABCD是正方形,
∵M为AD的中点,
(2)【解】连接OA,如图.
∵四边形ABCD是正方形,∴∠AOB=90°.
∵M为弧AD的中点,∴∠AOM=45°.∴∠BOM=∠AOB+∠AOM=135°.
6.B【点拨】如图,将正六边形分为6个全等的三角形.
∵拼成的四边形的面积为4,∴每一个三角形的面积为2.
∵剩余部分可分割为4个三角形,∴剩余部分的面积为8.
7.B【点拨】∵正方形草坪的边长为8m,∴正方形草坪的外接圆的半径是则其外接圆的面积是∵每个喷水龙头喷洒的面积是3 ×π=9π(m ),∴32π÷9π=4(个).
8.C【点拨】∵红点每6秒闪亮的顶点会转动1周,而751÷6=125……1,
∴经过751秒后,红点闪到了点F处.
∵蓝点每3秒闪亮的顶点会转动1周,而751÷3=250……1,
∴经过751秒后,蓝点闪到了点D处.
连接FD,过点E作EH⊥FD于点H,如图.
∵“六边形ABCDEF是正六边形,∴∠DEF=120°,EF=ED.∴∠EFH=30°,FD=2FH.
即经过751秒后,两个闪亮的顶点之间的距离是
9.B【点拨】如图,连接OE,
根据DE≥OD-OE,可知当D,E,O三点共线,即点E位于点E'处时,DE最小.
∵边长为2的△ABC是等边三角形,点A的坐标为(0,6),BC的中点D在y轴上,
∴AD⊥BC,OA=6,BD=CD=BC=1.
∵正六边形的边长为2,∴EF=2,∠EOF=60°,OE=OF.∴△EOF是等边三角形.
即DE的最小值为
10.【解】(1)∵五边形ABCDE是正五边形,
(2)△AMN是正三角形.
理由如下:连接ON,NF,如图.
由题意可得FN=OF=ON,∴△FON是正三角形.∴∠NFA=60°.∴∠NMA=60°.
同理可得∠ANM=60°,∴△AMN是正三角形.
(3)如图,连接OD.∵∠AMN=60°,∴∠AON=120°.
∴∠NOD=∠AOD-∠AON=144°-120°=24°.
∴n的值是15.
11.(1)【证明】如图①,延长BP至E,使PE=PC,连接CE.
∵A,B,P,C四点共圆,∴∠BAC+∠BPC=180°.
∵∠BPC+∠EPC=180°,∴∠CPE=∠BAC=60°.
又∵PE=PC,∴△PCE是正三角形,∴CE=PC,∠PCE=60°.
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP.
∵△ABC,△PCE都为正三角形,∴CE=PC,AC=BC,
∴△ECB≌△PCA(SAS),∴PA=BE=PB+PE=PB+PC.
(2)【证明】如图②,连接OA,OB,过点B作BE⊥PB交PA于点E.
∵∠1+∠2=∠2+∠3=90°,∴∠1=∠3.
又∵AB=BC,∴△ABE≌△CBP,∴PC=AE.
(3)【解】证明如下:如图③,过点B作BM⊥AP于点M,在AP上截取AQ=CP,连接BQ.
∵∠BAP=∠BCP,AB=BC,AQ=CP,∴△ABQ≌△CBP.∴BQ=BP.∴MP=QM.
易得∠APB=30°,∴BM=PB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
