24.4 弧长和扇形面积 第1课时 弧长和扇形面积 同步练习(含答案)
文档属性
| 名称 | 24.4 弧长和扇形面积 第1课时 弧长和扇形面积 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 445.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积
基础提优题
1.已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π B.6π C.3π D.4π
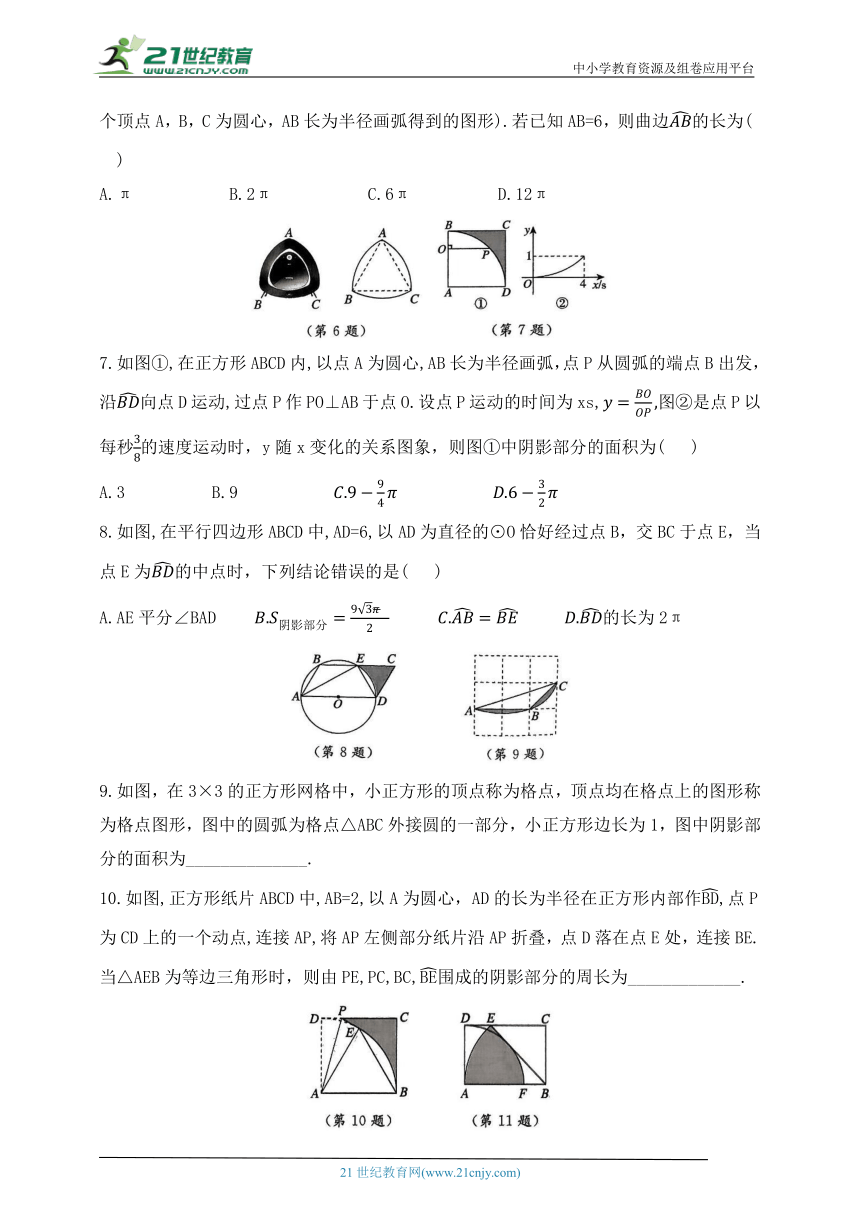
2.如图,四边形ABCD内接于半径为3的⊙O,CD是直径,若∠ABC=110°,则扇形AOD的面积为( )
A.B.π C. D.2π
3.如图,用一个半径为6cm的定滑轮带动重物上升,假设绳索(粗细不计)与滑轮之间没有滑动,绳索端点G向下移动了3πcm,则滑轮上的点F旋转了( )
A.60° B.90° C.120° D.45°
4.如图,C为⊙O上一点,AB是⊙O的直径,AB=4,∠ABC=30°,现将△ABC绕点B按顺时针方向旋转30°后得到△A'BC',BC'交⊙O于点D,则图中阴影部分的面积为_____________.
5铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,AB所在圆的圆心C恰好是△ABO的内心,若则花窗的周长(图中实线部分的长度)为______________.(结果保留π)
综合应用题
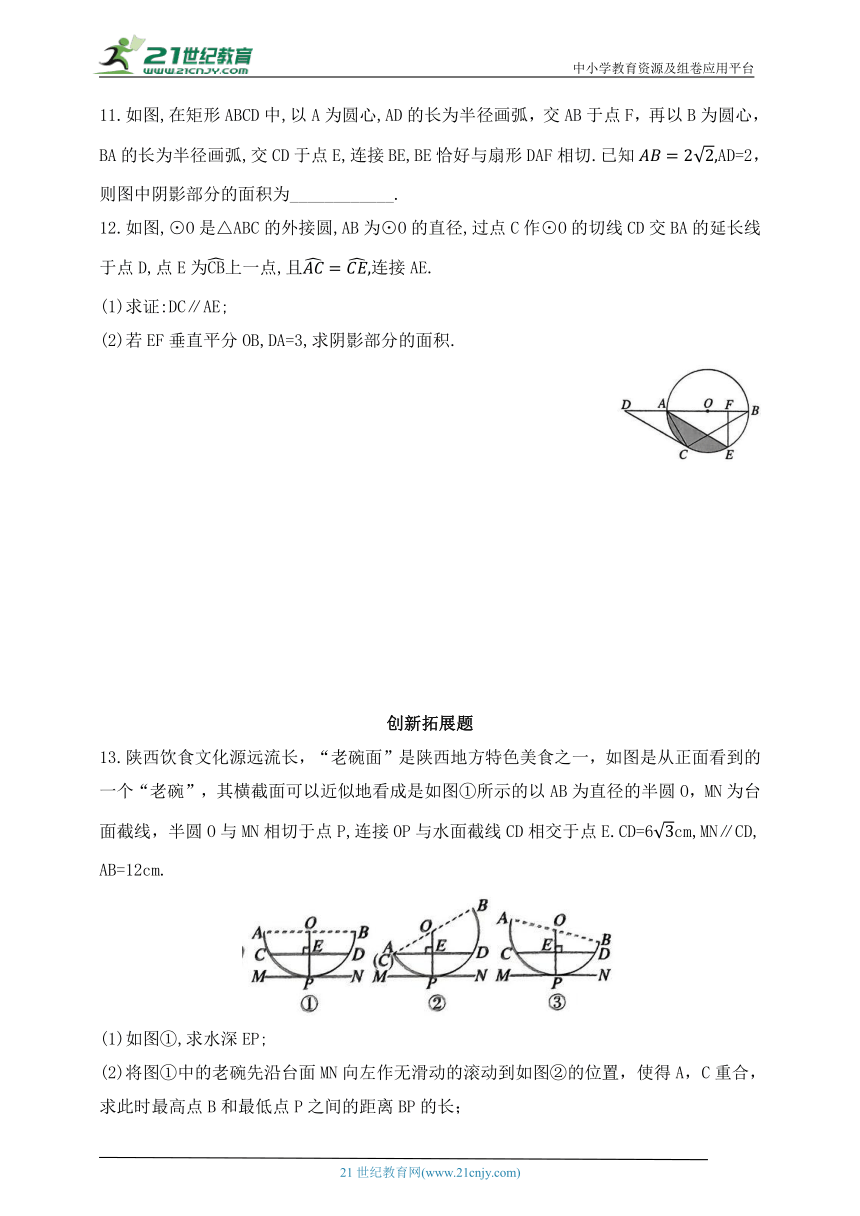
6.如图,某款扫地机器人的俯视图是一个等宽曲边三角形ABC(分别以正三角形ABC的三个顶点A,B,C为圆心,AB长为半径画弧得到的图形).若已知AB=6,则曲边的长为( )
A.π B.2π C.6π D.12π
7.如图①,在正方形ABCD内,以点A为圆心,AB长为半径画弧,点P从圆弧的端点B出发,沿向点D运动,过点P作PO⊥AB于点O.设点P运动的时间为xs,图②是点P以每秒的速度运动时,y随x变化的关系图象,则图①中阴影部分的面积为( )
A.3 B.9
8.如图,在平行四边形ABCD中,AD=6,以AD为直径的⊙O恰好经过点B,交BC于点E,当点E为的中点时,下列结论错误的是( )
A.AE平分∠BAD的长为2π
9.如图,在3×3的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点△ABC外接圆的一部分,小正方形边长为1,图中阴影部分的面积为______________.
10.如图,正方形纸片ABCD中,AB=2,以A为圆心,AD的长为半径在正方形内部作,点P为CD上的一个动点,连接AP,将AP左侧部分纸片沿AP折叠,点D落在点E处,连接BE.当△AEB为等边三角形时,则由PE,PC,BC,围成的阴影部分的周长为_____________.
11.如图,在矩形ABCD中,以A为圆心,AD的长为半径画弧,交AB于点F,再以B为圆心,BA的长为半径画弧,交CD于点E,连接BE,BE恰好与扇形DAF相切.已知AD=2,则图中阴影部分的面积为____________.
12.如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作⊙O的切线CD交BA的延长线于点D,点E为上一点,且连接AE.
(1)求证:DC∥AE;
(2)若EF垂直平分OB,DA=3,求阴影部分的面积.
创新拓展题
13.陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一,如图是从正面看到的一个“老碗”,其横截面可以近似地看成是如图①所示的以AB为直径的半圆O,MN为台面截线,半圆O与MN相切于点P,连接OP与水面截线CD相交于点E.CD=6cm,MN∥CD,AB=12cm.
(1)如图①,求水深EP;
(2)将图①中的老碗先沿台面MN向左作无滑动的滚动到如图②的位置,使得A,C重合,求此时最高点B和最低点P之间的距离BP的长;
(3)将碗从(2)中的位置开始向右作无滑动的滚动到图③所示时停止,若此时∠BOP=75°,求滚动过程中圆心O运动的路径长.
参考答案
1.D
2.B【点拨】∵∠ABC=110°,∴优弧,ADC所对的圆心角的度数为110°×2=220°.∵CD是直径,∴∠COD=180°.∵∠COD+∠AOD=220°,∴∠AOD=40°.∵⊙O的半径为3,∴扇形AOD的面积为故选B.
3.B 4.
5.8π【点拨】如图,过点C作CM⊥AB于点M,则AM=
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴△AOB是正三角形.
∵点C是△AOB的内心,
∠CBA=120°.
在Rt△ACM中,∠CAM=30°,∴AC=2CM,AC -CM =AM .
∴AB的长为∴花窗的周长为
6.B
7.C【点拨】由图象可得,当x=4时,∴OB=OP,此时P,D重合,O,A重合.
的长为即
∴AB=3.∴阴影部分的面积为
8.B【点拨】∵点E为的中点,,DE.∴∠BAE=∠EAD,∴AE平分A∠BAD,
故A选项正确,不符合题意.如图,连接OB,OE.
∵四边形ABCD是平行四边形,∴BE∥AO,∴∠BEA=∠EAO.
∵∠BAE=∠EAO,∴∠BAE=
60°.
∵OA=OB=OE,∴△AOB和△BOE都是等边三角形.∴OA=OB=BE.
∵BC=AD,∴EC=OD.
∵EC∥OD,∴四边形ECDO是平行四边形.过点E作EH⊥AD,垂足为H.
在Rt△EHO中,∠EOD=60°,∴∠OEH=30°.
∵OE=3,∴EH=故B选项错误,
符合题意.故C选项正确,不符合题意.
的长为故D选项正确,不符合题意.故选B.
【点拨】如图,作AB的垂直平分线MN,作BC的垂直平分线PQ,设MN与PQ相交于点O,则点O是△ABC外接圆的圆心,连接OA,OB,OC.
由题意得
∴△AOC是等腰直角三角形,且∠AOC=90°.
∴
【点拨】∵四边形ABCD是正方形,∴CD=BC=AB=2.
∵将AP左侧部分纸片沿AP折叠,点D落在点E处,
∴PD=PE.∴PE+PC=PD+PC=CD=2.
∵△AEB为等边三角形,∴∠BAE=60°,AE=AB=2.
阴影部分的周长为PE+PC+
【点拨】设BE与扇形ADF的切C点为G,如图,连接AE,AG,则AG⊥BE,过点E作EH⊥AB,交AB于点H.
∵四边形ABCD是矩形,∴BC=AD=2,CD=
由题意可得,BE=AB=2.
在Rt△BCE中,由勾股定理,得CE=2-2,CE=BC.∴∠CBE=45°.∴∠ABE=45°,即扇形BAE的圆心角为45°.
在Rt△DAE和Rt△GAE中,∴Rt△DAE≌Rt△GAE(HL).∴EG=DE=45°,即扇形AGF的圆心角为45°.∴
(1)【证明】如图,连接OC.
∵CD为⊙O的切线,点C在⊙O上,∴∠OCD=90°,即∠DCA+∠OCA=90°.
听闻AB为⊙O的直径,∴∠ACB=90°,即∠OCB+∠OCA=90°.∴∠DCA=∠OCB.
∵OC=OB,∴∠OCB=∠OBC.
∵,∴∠OBC=∠CAE.∴∠DCA=∠CAE.∴DC∥AE.
(2)【解】如图,连接OE,BE.
∵EF垂直平分OB,∴OE=BE.
又∵OE=OB,∴OE=OB=BE.∴△OEB为等边三角形.∴∠BOE=60°.∴∠AOE=120°.
又∵OA=OE,∴∠OAE=∠OEA=30°
又∵DC∥AE,∴∠D=∠OAE=30°.
又∵∠OCD=90°,∴∠DOC=60°.
又∵OA=OC,∴△AOC为等边三角形.∴∠OCA=60°,OA=AC.
∴∠DCA=30°.∴∠D=∠DCA.∴DA=AC=OA=OE=OB=3.
∴
又∵
13.【解】(1)连接OC,如图①所示.
易得
在Rt△OCE中,由勾股定理可得3(cm),
∴EP=OP-OE=6-3=3(cm).
(2)过点B作AD的平行线与PO的延长线相交于点F,如图②所示.
∵AD∥BF,∴∠OAE=∠OBF.
又∵AO=BO,∠AOE=∠BOF,∴△AOE≌△BOF(ASA).
由(1)知
'mn
连接BP,在Rt△BFP中,由勾股定理可得BP=
(3)连接OC,如图③所示.
由(1)可知OE=3cm,OC=6cm,
在Rt△COE中,易得∠COE=60°.
∵∠BOP=75°,∴∠AOC=180°-60°-75°=45°.由题意可得,圆心O运动的路径长为AC的长度
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积
基础提优题
1.已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π B.6π C.3π D.4π
2.如图,四边形ABCD内接于半径为3的⊙O,CD是直径,若∠ABC=110°,则扇形AOD的面积为( )
A.B.π C. D.2π
3.如图,用一个半径为6cm的定滑轮带动重物上升,假设绳索(粗细不计)与滑轮之间没有滑动,绳索端点G向下移动了3πcm,则滑轮上的点F旋转了( )
A.60° B.90° C.120° D.45°
4.如图,C为⊙O上一点,AB是⊙O的直径,AB=4,∠ABC=30°,现将△ABC绕点B按顺时针方向旋转30°后得到△A'BC',BC'交⊙O于点D,则图中阴影部分的面积为_____________.
5铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,AB所在圆的圆心C恰好是△ABO的内心,若则花窗的周长(图中实线部分的长度)为______________.(结果保留π)
综合应用题
6.如图,某款扫地机器人的俯视图是一个等宽曲边三角形ABC(分别以正三角形ABC的三个顶点A,B,C为圆心,AB长为半径画弧得到的图形).若已知AB=6,则曲边的长为( )
A.π B.2π C.6π D.12π
7.如图①,在正方形ABCD内,以点A为圆心,AB长为半径画弧,点P从圆弧的端点B出发,沿向点D运动,过点P作PO⊥AB于点O.设点P运动的时间为xs,图②是点P以每秒的速度运动时,y随x变化的关系图象,则图①中阴影部分的面积为( )
A.3 B.9
8.如图,在平行四边形ABCD中,AD=6,以AD为直径的⊙O恰好经过点B,交BC于点E,当点E为的中点时,下列结论错误的是( )
A.AE平分∠BAD的长为2π
9.如图,在3×3的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点△ABC外接圆的一部分,小正方形边长为1,图中阴影部分的面积为______________.
10.如图,正方形纸片ABCD中,AB=2,以A为圆心,AD的长为半径在正方形内部作,点P为CD上的一个动点,连接AP,将AP左侧部分纸片沿AP折叠,点D落在点E处,连接BE.当△AEB为等边三角形时,则由PE,PC,BC,围成的阴影部分的周长为_____________.
11.如图,在矩形ABCD中,以A为圆心,AD的长为半径画弧,交AB于点F,再以B为圆心,BA的长为半径画弧,交CD于点E,连接BE,BE恰好与扇形DAF相切.已知AD=2,则图中阴影部分的面积为____________.
12.如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作⊙O的切线CD交BA的延长线于点D,点E为上一点,且连接AE.
(1)求证:DC∥AE;
(2)若EF垂直平分OB,DA=3,求阴影部分的面积.
创新拓展题
13.陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一,如图是从正面看到的一个“老碗”,其横截面可以近似地看成是如图①所示的以AB为直径的半圆O,MN为台面截线,半圆O与MN相切于点P,连接OP与水面截线CD相交于点E.CD=6cm,MN∥CD,AB=12cm.
(1)如图①,求水深EP;
(2)将图①中的老碗先沿台面MN向左作无滑动的滚动到如图②的位置,使得A,C重合,求此时最高点B和最低点P之间的距离BP的长;
(3)将碗从(2)中的位置开始向右作无滑动的滚动到图③所示时停止,若此时∠BOP=75°,求滚动过程中圆心O运动的路径长.
参考答案
1.D
2.B【点拨】∵∠ABC=110°,∴优弧,ADC所对的圆心角的度数为110°×2=220°.∵CD是直径,∴∠COD=180°.∵∠COD+∠AOD=220°,∴∠AOD=40°.∵⊙O的半径为3,∴扇形AOD的面积为故选B.
3.B 4.
5.8π【点拨】如图,过点C作CM⊥AB于点M,则AM=
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴△AOB是正三角形.
∵点C是△AOB的内心,
∠CBA=120°.
在Rt△ACM中,∠CAM=30°,∴AC=2CM,AC -CM =AM .
∴AB的长为∴花窗的周长为
6.B
7.C【点拨】由图象可得,当x=4时,∴OB=OP,此时P,D重合,O,A重合.
的长为即
∴AB=3.∴阴影部分的面积为
8.B【点拨】∵点E为的中点,,DE.∴∠BAE=∠EAD,∴AE平分A∠BAD,
故A选项正确,不符合题意.如图,连接OB,OE.
∵四边形ABCD是平行四边形,∴BE∥AO,∴∠BEA=∠EAO.
∵∠BAE=∠EAO,∴∠BAE=
60°.
∵OA=OB=OE,∴△AOB和△BOE都是等边三角形.∴OA=OB=BE.
∵BC=AD,∴EC=OD.
∵EC∥OD,∴四边形ECDO是平行四边形.过点E作EH⊥AD,垂足为H.
在Rt△EHO中,∠EOD=60°,∴∠OEH=30°.
∵OE=3,∴EH=故B选项错误,
符合题意.故C选项正确,不符合题意.
的长为故D选项正确,不符合题意.故选B.
【点拨】如图,作AB的垂直平分线MN,作BC的垂直平分线PQ,设MN与PQ相交于点O,则点O是△ABC外接圆的圆心,连接OA,OB,OC.
由题意得
∴△AOC是等腰直角三角形,且∠AOC=90°.
∴
【点拨】∵四边形ABCD是正方形,∴CD=BC=AB=2.
∵将AP左侧部分纸片沿AP折叠,点D落在点E处,
∴PD=PE.∴PE+PC=PD+PC=CD=2.
∵△AEB为等边三角形,∴∠BAE=60°,AE=AB=2.
阴影部分的周长为PE+PC+
【点拨】设BE与扇形ADF的切C点为G,如图,连接AE,AG,则AG⊥BE,过点E作EH⊥AB,交AB于点H.
∵四边形ABCD是矩形,∴BC=AD=2,CD=
由题意可得,BE=AB=2.
在Rt△BCE中,由勾股定理,得CE=2-2,CE=BC.∴∠CBE=45°.∴∠ABE=45°,即扇形BAE的圆心角为45°.
在Rt△DAE和Rt△GAE中,∴Rt△DAE≌Rt△GAE(HL).∴EG=DE=45°,即扇形AGF的圆心角为45°.∴
(1)【证明】如图,连接OC.
∵CD为⊙O的切线,点C在⊙O上,∴∠OCD=90°,即∠DCA+∠OCA=90°.
听闻AB为⊙O的直径,∴∠ACB=90°,即∠OCB+∠OCA=90°.∴∠DCA=∠OCB.
∵OC=OB,∴∠OCB=∠OBC.
∵,∴∠OBC=∠CAE.∴∠DCA=∠CAE.∴DC∥AE.
(2)【解】如图,连接OE,BE.
∵EF垂直平分OB,∴OE=BE.
又∵OE=OB,∴OE=OB=BE.∴△OEB为等边三角形.∴∠BOE=60°.∴∠AOE=120°.
又∵OA=OE,∴∠OAE=∠OEA=30°
又∵DC∥AE,∴∠D=∠OAE=30°.
又∵∠OCD=90°,∴∠DOC=60°.
又∵OA=OC,∴△AOC为等边三角形.∴∠OCA=60°,OA=AC.
∴∠DCA=30°.∴∠D=∠DCA.∴DA=AC=OA=OE=OB=3.
∴
又∵
13.【解】(1)连接OC,如图①所示.
易得
在Rt△OCE中,由勾股定理可得3(cm),
∴EP=OP-OE=6-3=3(cm).
(2)过点B作AD的平行线与PO的延长线相交于点F,如图②所示.
∵AD∥BF,∴∠OAE=∠OBF.
又∵AO=BO,∠AOE=∠BOF,∴△AOE≌△BOF(ASA).
由(1)知
'mn
连接BP,在Rt△BFP中,由勾股定理可得BP=
(3)连接OC,如图③所示.
由(1)可知OE=3cm,OC=6cm,
在Rt△COE中,易得∠COE=60°.
∵∠BOP=75°,∴∠AOC=180°-60°-75°=45°.由题意可得,圆心O运动的路径长为AC的长度
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
