第二十四章 圆 阶段性测试题 与圆有关的计算(含答案)
文档属性
| 名称 | 第二十四章 圆 阶段性测试题 与圆有关的计算(含答案) | 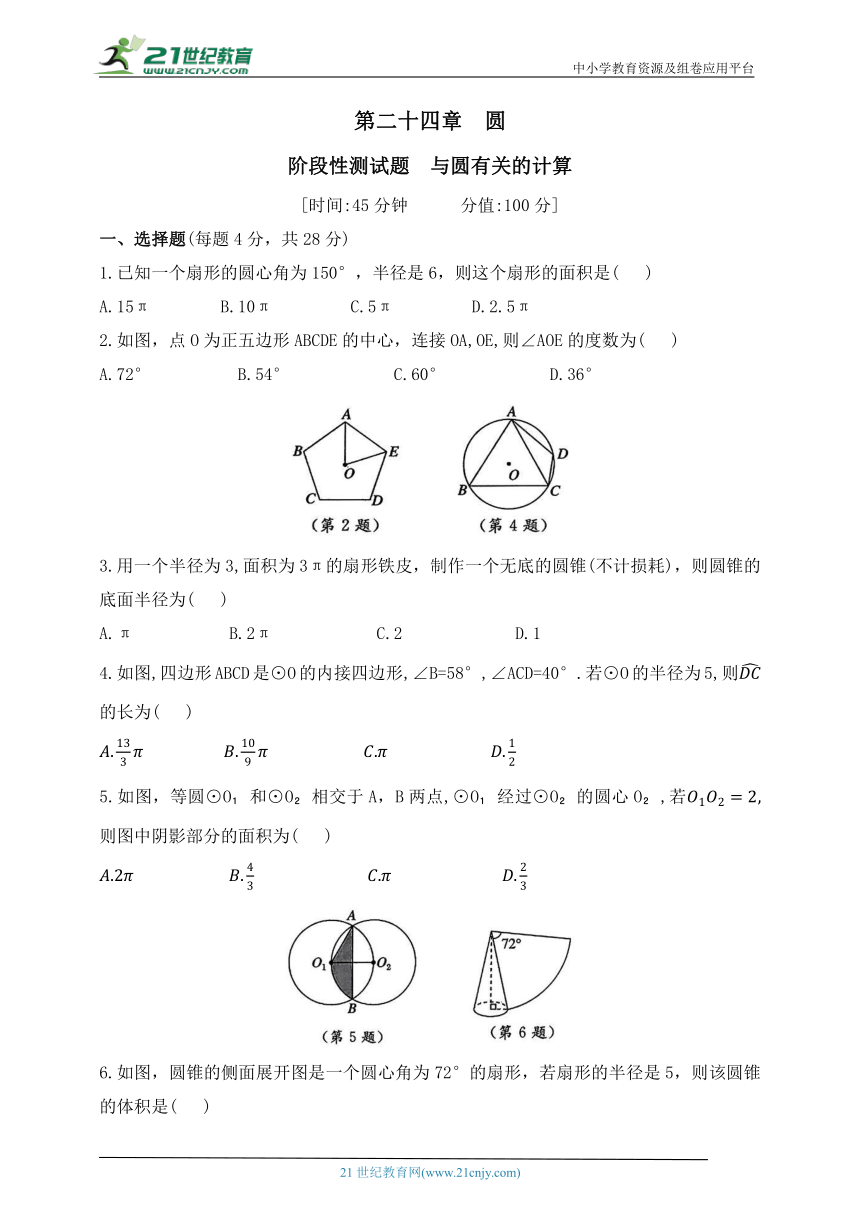 | |
| 格式 | docx | ||
| 文件大小 | 382.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:31:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
阶段性测试题 与圆有关的计算
[时间:45分钟 分值:100分]
一、选择题(每题4分,共28分)
1.已知一个扇形的圆心角为150°,半径是6,则这个扇形的面积是( )
A.15π B.10π C.5π D.2.5π
2.如图,点O为正五边形ABCDE的中心,连接OA,OE,则∠AOE的度数为( )
A.72° B.54° C.60° D.36°
3.用一个半径为3,面积为3π的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )
A.π B.2π C.2 D.1
4.如图,四边形ABCD是⊙O的内接四边形,∠B=58°,∠ACD=40°.若⊙O的半径为5,则的长为( )
5.如图,等圆⊙O 和⊙O 相交于A,B两点,⊙O 经过⊙O 的圆心O ,若则图中阴影部分的面积为( )
6.如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径是5,则该圆锥的体积是( )
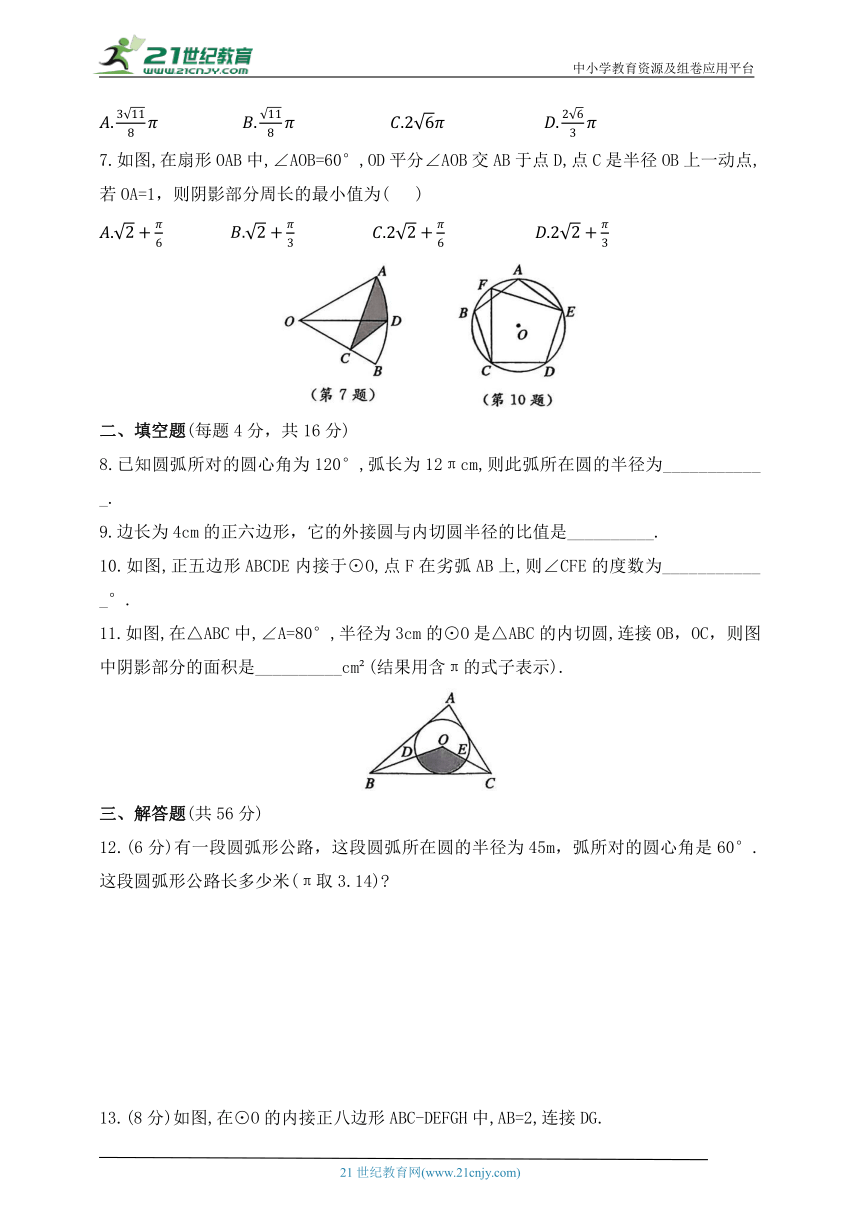
7.如图,在扇形OAB中,∠AOB=60°,OD平分∠AOB交AB于点D,点C是半径OB上一动点,若OA=1,则阴影部分周长的最小值为( )
二、填空题(每题4分,共16分)
8.已知圆弧所对的圆心角为120°,弧长为12πcm,则此弧所在圆的半径为____________.
9.边长为4cm的正六边形,它的外接圆与内切圆半径的比值是__________.
10.如图,正五边形ABCDE内接于⊙O,点F在劣弧AB上,则∠CFE的度数为____________°.
11.如图,在△ABC中,∠A=80°,半径为3cm的⊙O是△ABC的内切圆,连接OB,OC,则图中阴影部分的面积是__________cm (结果用含π的式子表示).
三、解答题(共56分)
12.(6分)有一段圆弧形公路,这段圆弧所在圆的半径为45m,弧所对的圆心角是60°.这段圆弧形公路长多少米(π取3.14)
13.(8分)如图,在⊙O的内接正八边形ABC-DEFGH中,AB=2,连接DG.
(1)求证:DG∥AB;
(2)DG的长为.
14.(12分)如图,一个圆锥的高为3cm,其侧面展开图是半圆形.求:
(1)圆锥的母线长与底面半径之比;
(2)∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
15.(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,G,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF与⊙O相切;
(2)当DB=BF=3时,求阴影部分的面积.
16.(18分)如图,是一个半圆形桥洞的截面示意图,圆心为O,直径AB是河底截线,弦CD是水位线,CD∥AB,AB=20m,OE⊥CD于点E.
(1)当测得水面宽(时.
①水位的高度OE=.
②水面以上的桥洞部分(即CD)的长为.
(2)当水位的高度比(1)上升1m时,有一艘宽为10m,船舱顶部高出水面2m的货船要经过桥洞(船舱截面为矩形MNPQ),请通过计算判断该货船能否顺利通过桥洞
参考答案
一、1.A 2.A 3.D
4.C【点拨】连接OC,OD.
∵四边形ABCD是⊙O的内接四边形,∠B=58°,
又∵∠ACD=40°,∴∠CAD=180°-∠ADC-∠ACD=18°.
5.D【点拨】连接BO ,BO ,设AB与O O 交于点H,如图.
∵⊙O 和⊙O 是等圆,⊙O 经过⊙O 的圆心O ,
∴△BO O 是等边三角形.
易知△AHO ≌△BHO ,
故选D.
6.D 7.A
二、8.18cm 10.72 11.
三、12.【解】这段圆弧形公路长为
答:这段圆弧形公路长约47.1m.
13.(1)【证明】如图,连接AD.
∵八边形ABCDEFGH是正八边形,
∴∠BAD=∠ADG.∴DG∥AB.
【点拨】∵八边形ABCDEFGH是正八边形,∴DE=EF=FG=AB=2,∠GFE=∠DEF=(8-2)×180°=135°.
如图,过点E作EP⊥DG于点P,过点F作FQ⊥DG于点Q,
同(1)可证EF∥DG,
在Rt△QGF中,∵∠DGF=45°,GF=2,
∴易得同理可得
∵EF∥DG,EP⊥DG,FQ⊥DG,
∴易得四边形PQFE是矩形.∴PQ=EF=2,
14.【解】(1)设此圆锥的底面半径为rcm,母线长AB=lcm.
∵2πr=πl,∴l=2r.∴l:r=2:1.
即圆锥的母线长与底面半径之比为2:1.
(2)由(1)知AB=AC=2BO=2CO.
∴AB=AC=BC,∴△ABC是等边三角形.∴∠BAC=60°.
(3)设OB=xcm,则AB=2xcm.由题意得(2x) ,解得(舍去).∴OB=3cm,AB=6cm.
∴圆锥的侧面积为
15.(1)【证明】∵AB=AC,∴∠C=∠OBD.
∵OD=OB,∴∠ODB=∠OBD,(∴∠ODB=∠C.∴OD∥AC.
∵EF⊥AC,∴EF⊥OD.
∵OD是⊙O的半径,∴EF是⊙O的切线.
(2)【解】∵BD=BF=3,∴∠BDF=∠F.
∵OD⊥EF,∴∠ODF=90°.
∴∠ODB=∠BOD.
又∵∠ODB=∠OBD,∴∠ODB=∠OBD=∠BOD=60°.
∴OB=OD=DB=3,∠F=∠BDF=30°.∴DB=BF=3.
∴OF=6,∴DF=3
16.【解】(1)①5m②πm【点拨】①连接OD.
又
∴水位的高度
②连接OC.由①易得∠DOE=60°.
∵OC=OD,OE⊥CD,∴∠COD=2∠DOE=120°.
∴水面以上的桥洞部分(即(CD)的长为
(2)由(1)中水位高度为5m可知此时水位高度OE=5+1=6(m).
延长OE交MQ于点F,则OF⊥MQ,连接OM.
∵货船宽为10m,船舱顶部高出水面2m,
∴OF=6+2=8(m),货船居中行驶时
又∵半圆形桥洞的半径
∴该货船能顺利通过桥洞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
阶段性测试题 与圆有关的计算
[时间:45分钟 分值:100分]
一、选择题(每题4分,共28分)
1.已知一个扇形的圆心角为150°,半径是6,则这个扇形的面积是( )
A.15π B.10π C.5π D.2.5π
2.如图,点O为正五边形ABCDE的中心,连接OA,OE,则∠AOE的度数为( )
A.72° B.54° C.60° D.36°
3.用一个半径为3,面积为3π的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )
A.π B.2π C.2 D.1
4.如图,四边形ABCD是⊙O的内接四边形,∠B=58°,∠ACD=40°.若⊙O的半径为5,则的长为( )
5.如图,等圆⊙O 和⊙O 相交于A,B两点,⊙O 经过⊙O 的圆心O ,若则图中阴影部分的面积为( )
6.如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径是5,则该圆锥的体积是( )
7.如图,在扇形OAB中,∠AOB=60°,OD平分∠AOB交AB于点D,点C是半径OB上一动点,若OA=1,则阴影部分周长的最小值为( )
二、填空题(每题4分,共16分)
8.已知圆弧所对的圆心角为120°,弧长为12πcm,则此弧所在圆的半径为____________.
9.边长为4cm的正六边形,它的外接圆与内切圆半径的比值是__________.
10.如图,正五边形ABCDE内接于⊙O,点F在劣弧AB上,则∠CFE的度数为____________°.
11.如图,在△ABC中,∠A=80°,半径为3cm的⊙O是△ABC的内切圆,连接OB,OC,则图中阴影部分的面积是__________cm (结果用含π的式子表示).
三、解答题(共56分)
12.(6分)有一段圆弧形公路,这段圆弧所在圆的半径为45m,弧所对的圆心角是60°.这段圆弧形公路长多少米(π取3.14)
13.(8分)如图,在⊙O的内接正八边形ABC-DEFGH中,AB=2,连接DG.
(1)求证:DG∥AB;
(2)DG的长为.
14.(12分)如图,一个圆锥的高为3cm,其侧面展开图是半圆形.求:
(1)圆锥的母线长与底面半径之比;
(2)∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
15.(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,G,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF与⊙O相切;
(2)当DB=BF=3时,求阴影部分的面积.
16.(18分)如图,是一个半圆形桥洞的截面示意图,圆心为O,直径AB是河底截线,弦CD是水位线,CD∥AB,AB=20m,OE⊥CD于点E.
(1)当测得水面宽(时.
①水位的高度OE=.
②水面以上的桥洞部分(即CD)的长为.
(2)当水位的高度比(1)上升1m时,有一艘宽为10m,船舱顶部高出水面2m的货船要经过桥洞(船舱截面为矩形MNPQ),请通过计算判断该货船能否顺利通过桥洞
参考答案
一、1.A 2.A 3.D
4.C【点拨】连接OC,OD.
∵四边形ABCD是⊙O的内接四边形,∠B=58°,
又∵∠ACD=40°,∴∠CAD=180°-∠ADC-∠ACD=18°.
5.D【点拨】连接BO ,BO ,设AB与O O 交于点H,如图.
∵⊙O 和⊙O 是等圆,⊙O 经过⊙O 的圆心O ,
∴△BO O 是等边三角形.
易知△AHO ≌△BHO ,
故选D.
6.D 7.A
二、8.18cm 10.72 11.
三、12.【解】这段圆弧形公路长为
答:这段圆弧形公路长约47.1m.
13.(1)【证明】如图,连接AD.
∵八边形ABCDEFGH是正八边形,
∴∠BAD=∠ADG.∴DG∥AB.
【点拨】∵八边形ABCDEFGH是正八边形,∴DE=EF=FG=AB=2,∠GFE=∠DEF=(8-2)×180°=135°.
如图,过点E作EP⊥DG于点P,过点F作FQ⊥DG于点Q,
同(1)可证EF∥DG,
在Rt△QGF中,∵∠DGF=45°,GF=2,
∴易得同理可得
∵EF∥DG,EP⊥DG,FQ⊥DG,
∴易得四边形PQFE是矩形.∴PQ=EF=2,
14.【解】(1)设此圆锥的底面半径为rcm,母线长AB=lcm.
∵2πr=πl,∴l=2r.∴l:r=2:1.
即圆锥的母线长与底面半径之比为2:1.
(2)由(1)知AB=AC=2BO=2CO.
∴AB=AC=BC,∴△ABC是等边三角形.∴∠BAC=60°.
(3)设OB=xcm,则AB=2xcm.由题意得(2x) ,解得(舍去).∴OB=3cm,AB=6cm.
∴圆锥的侧面积为
15.(1)【证明】∵AB=AC,∴∠C=∠OBD.
∵OD=OB,∴∠ODB=∠OBD,(∴∠ODB=∠C.∴OD∥AC.
∵EF⊥AC,∴EF⊥OD.
∵OD是⊙O的半径,∴EF是⊙O的切线.
(2)【解】∵BD=BF=3,∴∠BDF=∠F.
∵OD⊥EF,∴∠ODF=90°.
∴∠ODB=∠BOD.
又∵∠ODB=∠OBD,∴∠ODB=∠OBD=∠BOD=60°.
∴OB=OD=DB=3,∠F=∠BDF=30°.∴DB=BF=3.
∴OF=6,∴DF=3
16.【解】(1)①5m②πm【点拨】①连接OD.
又
∴水位的高度
②连接OC.由①易得∠DOE=60°.
∵OC=OD,OE⊥CD,∴∠COD=2∠DOE=120°.
∴水面以上的桥洞部分(即(CD)的长为
(2)由(1)中水位高度为5m可知此时水位高度OE=5+1=6(m).
延长OE交MQ于点F,则OF⊥MQ,连接OM.
∵货船宽为10m,船舱顶部高出水面2m,
∴OF=6+2=8(m),货船居中行驶时
又∵半圆形桥洞的半径
∴该货船能顺利通过桥洞.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
