第二十四章 圆 阶段性测试题 圆及圆的基本性质(含答案)
文档属性
| 名称 | 第二十四章 圆 阶段性测试题 圆及圆的基本性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 440.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:32:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
阶段性测试题 圆及圆的基本性质
[时间:45分钟 分值:100分]
一、选择题(每题3分,共30分)
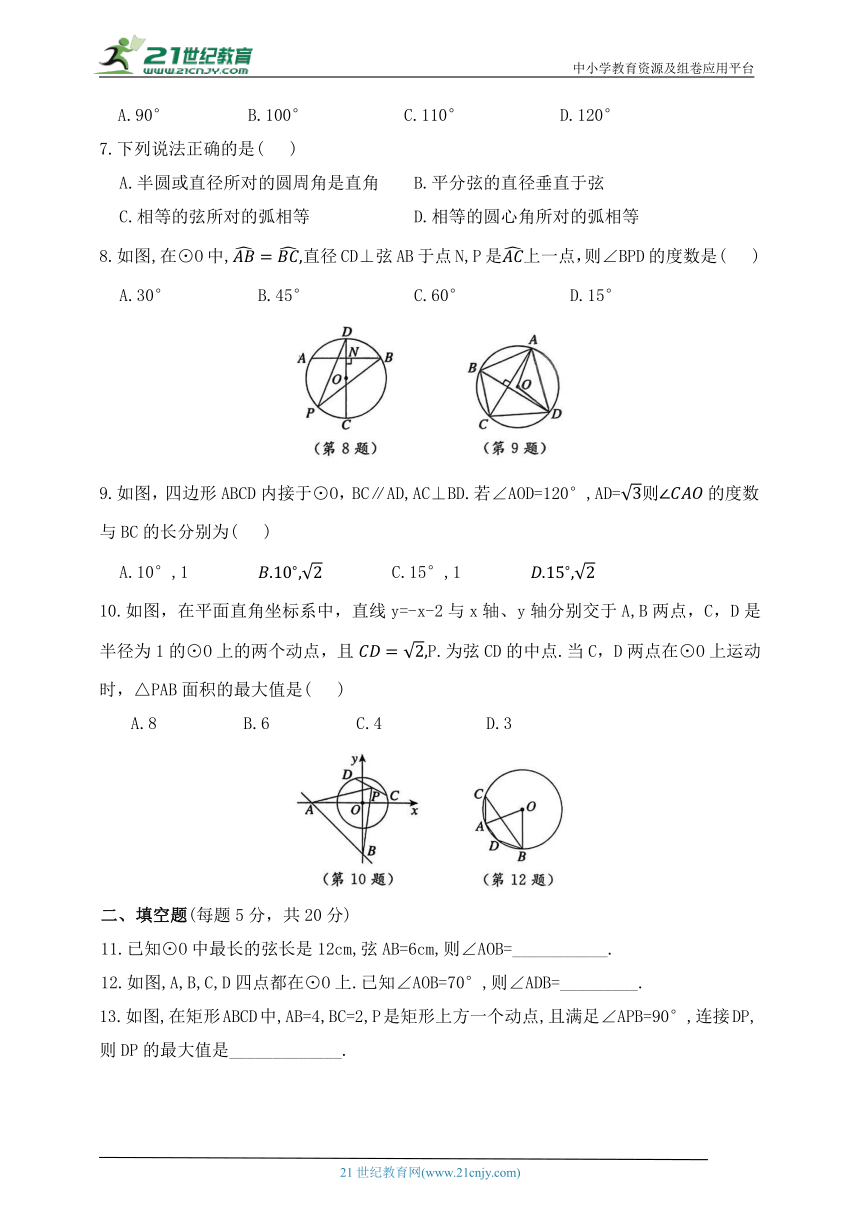
1.如图,在以原点为圆心,2为半径的⊙O上有一点C,∠COA=45°,则点C的坐标为( )
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=2OE,则∠BCD的度数为( )
A.15° B.22.5° C.30° D.45°
3.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=( )
A.72° B.62° C.52° D.28°
4.如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连接OB,OC,若∠DOE=130°,则∠BOC的度数为( )
A.95° B.100° C.105° D.130°
5.如图,AB是⊙O的直径,点C在圆上,将沿AC翻折与AB交于点D.若BC所对的圆心角的度数为30°,则.所对的圆心角的度数为( )
A.100° B.120° C.60° D.30°
6.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100° C.110° D.120°
7.下列说法正确的是( )
A.半圆或直径所对的圆周角是直角 B.平分弦的直径垂直于弦
C.相等的弦所对的弧相等 D.相等的圆心角所对的弧相等
8.如图,在⊙O中,直径CD⊥弦AB于点N,P是上一点,则∠BPD的度数是( )
A.30° B.45° C.60° D.15°
9.如图,四边形ABCD内接于⊙O,BC∥AD,AC⊥BD.若∠AOD=120°,AD=则的度数与BC的长分别为( )
A.10°,1 C.15°,1
10.如图,在平面直角坐标系中,直线y=-x-2与x轴、y轴分别交于A,B两点,C,D是半径为1的⊙O上的两个动点,且P.为弦CD的中点.当C,D两点在⊙O上运动时,△PAB面积的最大值是( )
A.8 B.6 C.4 D.3
二、填空题(每题5分,共20分)
11.已知⊙O中最长的弦长是12cm,弦AB=6cm,则∠AOB=___________.
12.如图,A,B,C,D四点都在⊙O上.已知∠AOB=70°,则∠ADB=_________.
13.如图,在矩形ABCD中,AB=4,BC=2,P是矩形上方一个动点,且满足∠APB=90°,连接DP,则DP的最大值是_____________.
14.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高,底面直径,球的最高点到瓶底面的距离为,则球的半径为__________(玻璃瓶厚度忽略不计).
三、解答题(共50分)
15.(10分)如图,A,B,C,D是⊙O上四点,且AD=CB.求证:AB=CD.
16.(13分)如图,已知在⊙O中,OC与AD相交于点E.求证:
(1)AD∥BC;
(2)四边形BCDE为菱形.
17.(13分)新考法构造直角三角形法/如图,已知AB是⊙O的直径,∠ACD是.所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F,若AB=4,求DF的长.
18.(14分)如图,在△ABC中,D是AB上一点,⊙O经过点A,C,D,交BC于点E,过点D作DF∥BC,交⊙O于点F,连接AF,EF,CF,AF=EF.
(1)求证:四边形DBCF是平行四边形;
(2)若D是AB的中点,求证:AC是⊙O的直径.
参考答案
一1.C 2.B 3.B 4.B 5.B
6.C【点拨】∵AB是⊙O的直径,∴∠ADB=90°.
又∵∠ABD=20°,∴∠DAB=70°.
∵四边形ABCD内接于⊙O,∴∠BAD+∠BCD=180°.∴∠BCD=110°.
7.A【点拨】选项B,如果“平分弦的直径垂直于弦”中的“弦”是直径,那么结论不一定成立.解题时容易忽略垂径定理的推论中“不是直径”这个条件而致错.选项C,D忽略了在同圆或等圆中这一前提,故选A.
8.A【点拨】连接OA,OB.∵直径CD⊥弦AB,.
又∵,∴.∴∠AOB=120°.
又∵AD=BD,∴∠BOD=60°.∴∠BPD=∠BOD=30°.
9.C【点拨】如图,设AC与BD的交点为F,连接OB,OC.
∵BC∥AD,∴∠DBC=∠ADB.∴AB=CD.∴∠CAD=∠BDA.
∵DB⊥AC,∴∠AFD=90°.∴∠CAD=∠BDA=45°.
∴∠AOB=2∠ADB=90°,∠COD=2∠CAD=90°.
∵∠AOD=120°,∴∠BOC=360°-90°-90°-
又∵OB=OC,∴△OBC是等边三角形.∴BC=OB.
过点O作OE⊥AD于点E,
∵OA=OD,∠AOD=120°,AD=,∴∠OAD=∠ODA=30°,AE=DE=AD=.
易得OA=1.
∴BC=OB=OA=1.
10.D【点拨】如图,作OQ⊥AB,连接OP,OD,OC,PQ,
∵CD=,OC=OD=1,∴OC +OD =CD .∴△OCD为等腰直角三角形.
由y=-x-2,得A(-2,0),B(0,-2).∴OA=OB=2.
∵OA⊥OB,∴△OAB为等腰直角三角形.
易知当P,O,Q三点共线时,S△ABP最大.
∵P为弦CD的中点,∴易得OP=
即△PAB面积的最大值为3.
二、11.60° 12.145°
【点拨】∵∠APB=90°,∴点P在以AB的长为直径的圆上.
如图,取AB的中点为O,以OA的长为半径画半圆O,连接OP,连接DO并延长交半圆O于点P',
则OP'=
∵在△OPD中,,∴当P,O,D三点共线时,DP有最大值,最大值即为DP'的长.
∵四边形ABCD是矩形,∴∠DAO=90°,AD=BC=2.∴OD=
14.7.5【点拨】如图,设球心为O,连接OA,AD,过点O作OM⊥AD于点M.
设球的半径为rcm,由题意得AD=12cm,OM=32-20-r=(12-r)cm.
由垂径定理得6cm.
在Rt△OAM中,AM +OM =OA ,即,解得r=7.5.
∴球的半径为7.5cm.
三、15.【证明】设AB,CD交于点E.
∵∠ADC=∠ABC,∠BAD=∠BCD,AD=CB,∴△ADE≌△CBE.∴AE=CE,DE=BE.
∴AE+EB=CE+ED,即AB=CD.
16.【证明】(1)如图,连接BD.
∵AB=CD,∴∠ADB=∠CBD.∴AD∥BC.
(2)如图,设OC与BD相交于点F.
OC为⊙O的半径,∴BF=DF,OC⊥BD.
又∵∠EDF=∠CBF,∠DFE=∠BFC,∴△DEF≌△BCF.∴EF=CF.
∴四边形BCDE是菱形.
点规律 判定菱形的条件:1.从边上看:四边形的四边相等或平行四边形的一组邻边相等;
2.从对角线看:四边形的对角线互相垂直平分或平行四边形的对角线互相垂直.
17.【解】(1)连接BD.
∵∠ACD=30°,∴∠B=∠ACD=30°.
∵AB是⊙O的直径,∴∠ADB=90°.
(2)∵∠ADB=90°,∠B=30°,AB=4,
∵∠DAB=60°,DE⊥AB,且AB是直径,∴∠ADE=30°,DE=EF.∴AE=AD=1.
18.【证明】(1)连接DE.
∵点D,E,C,F四点共圆,∴∠EDF+∠ECF=180°.
∵AF=EF,∴∠ADF=∠EDF.
∵DF∥BC,∴∠ADF=∠B.
∴∠EDF=∠B.∴∠B+∠ECF=180°.∴BD∥CF.
又∵DF∥BC,∴四边形DBCF是平行四边形.
(2)连接CD.
由(1)得四边形DBCF是平行四边形.∴∠BAC=∠DFC=∠B.∴BC=AC.
∵D是AB的中点,∴CD⊥AB.∴∠ADC=90°.∴AC是⊙O的直径.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
阶段性测试题 圆及圆的基本性质
[时间:45分钟 分值:100分]
一、选择题(每题3分,共30分)
1.如图,在以原点为圆心,2为半径的⊙O上有一点C,∠COA=45°,则点C的坐标为( )
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=2OE,则∠BCD的度数为( )
A.15° B.22.5° C.30° D.45°
3.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=( )
A.72° B.62° C.52° D.28°
4.如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连接OB,OC,若∠DOE=130°,则∠BOC的度数为( )
A.95° B.100° C.105° D.130°
5.如图,AB是⊙O的直径,点C在圆上,将沿AC翻折与AB交于点D.若BC所对的圆心角的度数为30°,则.所对的圆心角的度数为( )
A.100° B.120° C.60° D.30°
6.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100° C.110° D.120°
7.下列说法正确的是( )
A.半圆或直径所对的圆周角是直角 B.平分弦的直径垂直于弦
C.相等的弦所对的弧相等 D.相等的圆心角所对的弧相等
8.如图,在⊙O中,直径CD⊥弦AB于点N,P是上一点,则∠BPD的度数是( )
A.30° B.45° C.60° D.15°
9.如图,四边形ABCD内接于⊙O,BC∥AD,AC⊥BD.若∠AOD=120°,AD=则的度数与BC的长分别为( )
A.10°,1 C.15°,1
10.如图,在平面直角坐标系中,直线y=-x-2与x轴、y轴分别交于A,B两点,C,D是半径为1的⊙O上的两个动点,且P.为弦CD的中点.当C,D两点在⊙O上运动时,△PAB面积的最大值是( )
A.8 B.6 C.4 D.3
二、填空题(每题5分,共20分)
11.已知⊙O中最长的弦长是12cm,弦AB=6cm,则∠AOB=___________.
12.如图,A,B,C,D四点都在⊙O上.已知∠AOB=70°,则∠ADB=_________.
13.如图,在矩形ABCD中,AB=4,BC=2,P是矩形上方一个动点,且满足∠APB=90°,连接DP,则DP的最大值是_____________.
14.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高,底面直径,球的最高点到瓶底面的距离为,则球的半径为__________(玻璃瓶厚度忽略不计).
三、解答题(共50分)
15.(10分)如图,A,B,C,D是⊙O上四点,且AD=CB.求证:AB=CD.
16.(13分)如图,已知在⊙O中,OC与AD相交于点E.求证:
(1)AD∥BC;
(2)四边形BCDE为菱形.
17.(13分)新考法构造直角三角形法/如图,已知AB是⊙O的直径,∠ACD是.所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F,若AB=4,求DF的长.
18.(14分)如图,在△ABC中,D是AB上一点,⊙O经过点A,C,D,交BC于点E,过点D作DF∥BC,交⊙O于点F,连接AF,EF,CF,AF=EF.
(1)求证:四边形DBCF是平行四边形;
(2)若D是AB的中点,求证:AC是⊙O的直径.
参考答案
一1.C 2.B 3.B 4.B 5.B
6.C【点拨】∵AB是⊙O的直径,∴∠ADB=90°.
又∵∠ABD=20°,∴∠DAB=70°.
∵四边形ABCD内接于⊙O,∴∠BAD+∠BCD=180°.∴∠BCD=110°.
7.A【点拨】选项B,如果“平分弦的直径垂直于弦”中的“弦”是直径,那么结论不一定成立.解题时容易忽略垂径定理的推论中“不是直径”这个条件而致错.选项C,D忽略了在同圆或等圆中这一前提,故选A.
8.A【点拨】连接OA,OB.∵直径CD⊥弦AB,.
又∵,∴.∴∠AOB=120°.
又∵AD=BD,∴∠BOD=60°.∴∠BPD=∠BOD=30°.
9.C【点拨】如图,设AC与BD的交点为F,连接OB,OC.
∵BC∥AD,∴∠DBC=∠ADB.∴AB=CD.∴∠CAD=∠BDA.
∵DB⊥AC,∴∠AFD=90°.∴∠CAD=∠BDA=45°.
∴∠AOB=2∠ADB=90°,∠COD=2∠CAD=90°.
∵∠AOD=120°,∴∠BOC=360°-90°-90°-
又∵OB=OC,∴△OBC是等边三角形.∴BC=OB.
过点O作OE⊥AD于点E,
∵OA=OD,∠AOD=120°,AD=,∴∠OAD=∠ODA=30°,AE=DE=AD=.
易得OA=1.
∴BC=OB=OA=1.
10.D【点拨】如图,作OQ⊥AB,连接OP,OD,OC,PQ,
∵CD=,OC=OD=1,∴OC +OD =CD .∴△OCD为等腰直角三角形.
由y=-x-2,得A(-2,0),B(0,-2).∴OA=OB=2.
∵OA⊥OB,∴△OAB为等腰直角三角形.
易知当P,O,Q三点共线时,S△ABP最大.
∵P为弦CD的中点,∴易得OP=
即△PAB面积的最大值为3.
二、11.60° 12.145°
【点拨】∵∠APB=90°,∴点P在以AB的长为直径的圆上.
如图,取AB的中点为O,以OA的长为半径画半圆O,连接OP,连接DO并延长交半圆O于点P',
则OP'=
∵在△OPD中,,∴当P,O,D三点共线时,DP有最大值,最大值即为DP'的长.
∵四边形ABCD是矩形,∴∠DAO=90°,AD=BC=2.∴OD=
14.7.5【点拨】如图,设球心为O,连接OA,AD,过点O作OM⊥AD于点M.
设球的半径为rcm,由题意得AD=12cm,OM=32-20-r=(12-r)cm.
由垂径定理得6cm.
在Rt△OAM中,AM +OM =OA ,即,解得r=7.5.
∴球的半径为7.5cm.
三、15.【证明】设AB,CD交于点E.
∵∠ADC=∠ABC,∠BAD=∠BCD,AD=CB,∴△ADE≌△CBE.∴AE=CE,DE=BE.
∴AE+EB=CE+ED,即AB=CD.
16.【证明】(1)如图,连接BD.
∵AB=CD,∴∠ADB=∠CBD.∴AD∥BC.
(2)如图,设OC与BD相交于点F.
OC为⊙O的半径,∴BF=DF,OC⊥BD.
又∵∠EDF=∠CBF,∠DFE=∠BFC,∴△DEF≌△BCF.∴EF=CF.
∴四边形BCDE是菱形.
点规律 判定菱形的条件:1.从边上看:四边形的四边相等或平行四边形的一组邻边相等;
2.从对角线看:四边形的对角线互相垂直平分或平行四边形的对角线互相垂直.
17.【解】(1)连接BD.
∵∠ACD=30°,∴∠B=∠ACD=30°.
∵AB是⊙O的直径,∴∠ADB=90°.
(2)∵∠ADB=90°,∠B=30°,AB=4,
∵∠DAB=60°,DE⊥AB,且AB是直径,∴∠ADE=30°,DE=EF.∴AE=AD=1.
18.【证明】(1)连接DE.
∵点D,E,C,F四点共圆,∴∠EDF+∠ECF=180°.
∵AF=EF,∴∠ADF=∠EDF.
∵DF∥BC,∴∠ADF=∠B.
∴∠EDF=∠B.∴∠B+∠ECF=180°.∴BD∥CF.
又∵DF∥BC,∴四边形DBCF是平行四边形.
(2)连接CD.
由(1)得四边形DBCF是平行四边形.∴∠BAC=∠DFC=∠B.∴BC=AC.
∵D是AB的中点,∴CD⊥AB.∴∠ADC=90°.∴AC是⊙O的直径.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
