第二十四章 圆 章末复习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
章末复习
核心考点整合
考点1 圆的有关概念
1.下列说法中,正确的是( )
A.过圆心的直线是圆的直径 B.直径是圆中最长的弦
C.相等长度的两条弧是等弧 D.顶点在圆上的角是圆周角
考点2 垂径定理及其推论
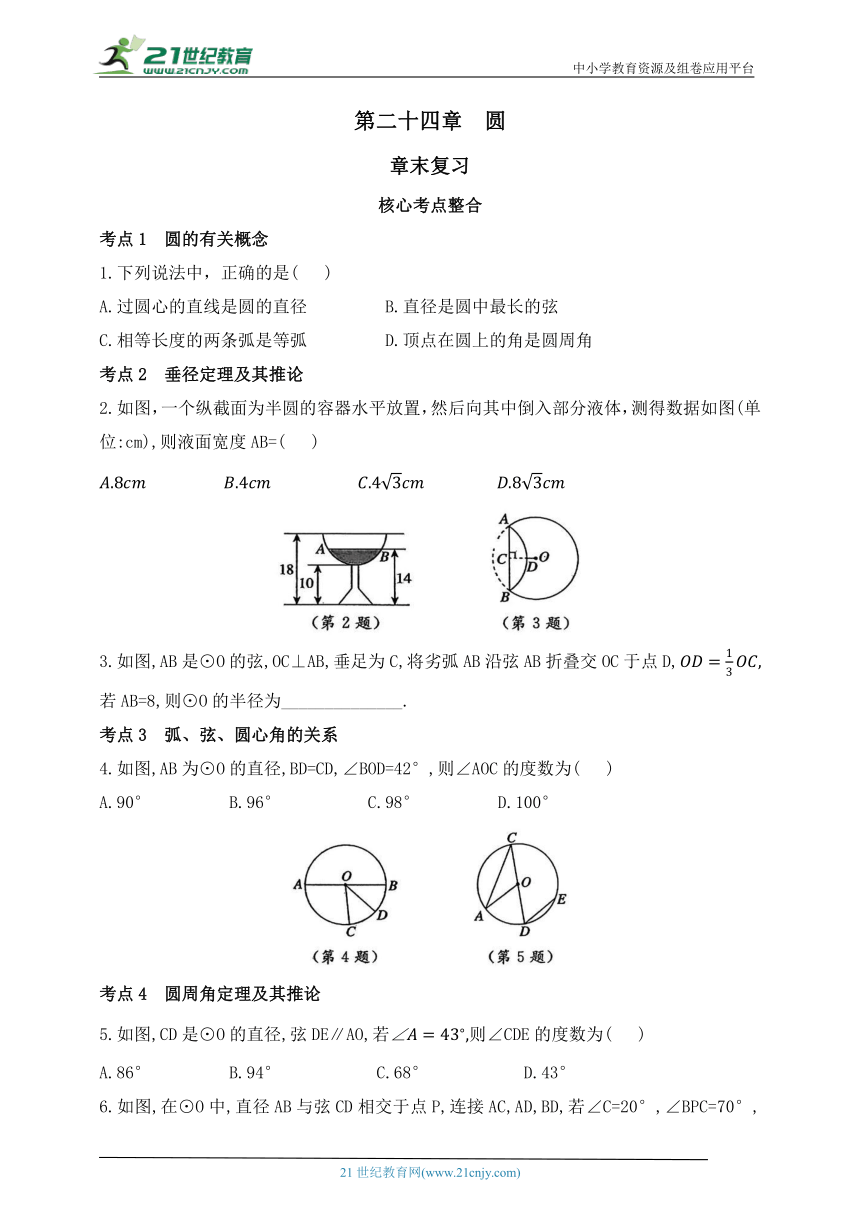
2.如图,一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图(单位:cm),则液面宽度AB=( )
3.如图,AB是⊙O的弦,OC⊥AB,垂足为C,将劣弧AB沿弦AB折叠交OC于点D,若AB=8,则⊙O的半径为______________.
考点3 弧、弦、圆心角的关系
4.如图,AB为⊙O的直径,BD=CD,∠BOD=42°,则∠AOC的度数为( )
A.90° B.96° C.98° D.100°
考点4 圆周角定理及其推论
5.如图,CD是⊙O的直径,弦DE∥AO,若则∠CDE的度数为( )
A.86° B.94° C.68° D.43°
6.如图,在⊙O中,直径AB与弦CD相交于点P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=( )
A.70° B.60° C.50° D.40°
考点5 点和圆、直线和圆的位置关系
7.在Rt△ABC中,∠C=90°,AC=2,AB=4,如果以点A为圆心,AC长为半径作⊙A,那么斜边AB的中点D在⊙A_________.(填“内”“上”或“外”)
8.如图,已知∠ACB=30°,CM=2,AM=5,以点M为圆心,r为半径作⊙M,当⊙M与线段AC有交点时,r的取值范围是______________.
考点6 切线的判定与性质
9.如图,AB是半圆O的直径,点C在半圆上(不与A,B重合),DE⊥AB于点D,交BC于点F,下列条件中能判断CE是半圆O的切线的是( )
A.∠E=∠CFE B.∠E=∠ECF C.∠ECF=∠EFC D.∠ECF=60°
10.如图,PA,PB是⊙O的切线,切点分别是A,B,点C在上,过点C的切线分别交PA,PB于点D,E.若PB=10,则△PDE的周长为_______________.
11.如图,AB为⊙O的直径,点C,D为圆上两点,连接AD,AC,CD,过点C作CE⊥AD交AD的延长线于E.
(1)求证:CE为⊙O的切线;
(2)若CD=4,CE=2求⊙O的半径.
考点7 三角形的外接圆与三角形的内切圆
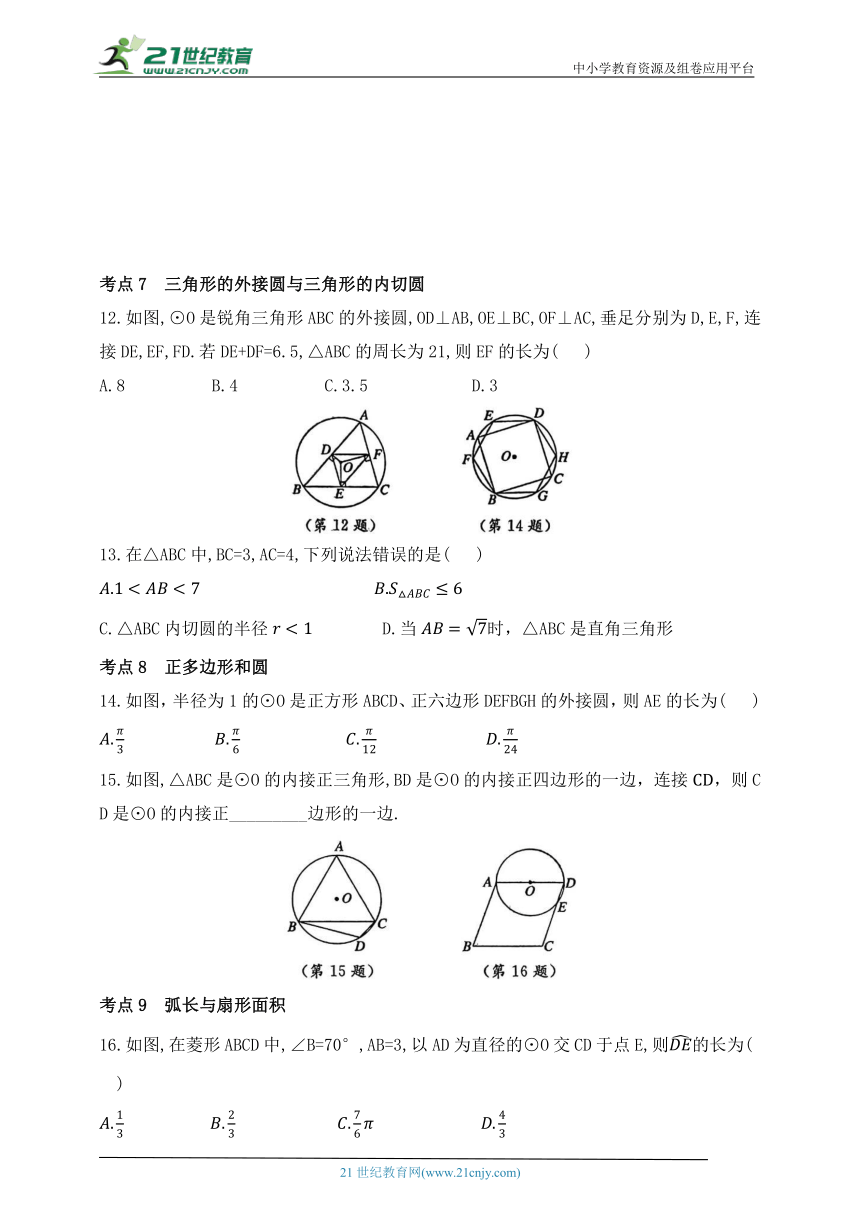
12.如图,⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为( )
A.8 B.4 C.3.5 D.3
13.在△ABC中,BC=3,AC=4,下列说法错误的是( )
C.△ABC内切圆的半径 D.当时,△ABC是直角三角形
考点8 正多边形和圆
14.如图,半径为1的⊙O是正方形ABCD、正六边形DEFBGH的外接圆,则AE的长为( )
15.如图,△ABC是⊙O的内接正三角形,BD是⊙O的内接正四边形的一边,连接,则CD是⊙O的内接正_________边形的一边.
考点9 弧长与扇形面积
16.如图,在菱形ABCD中,∠B=70°,AB=3,以AD为直径的⊙O交CD于点E,则的长为( )
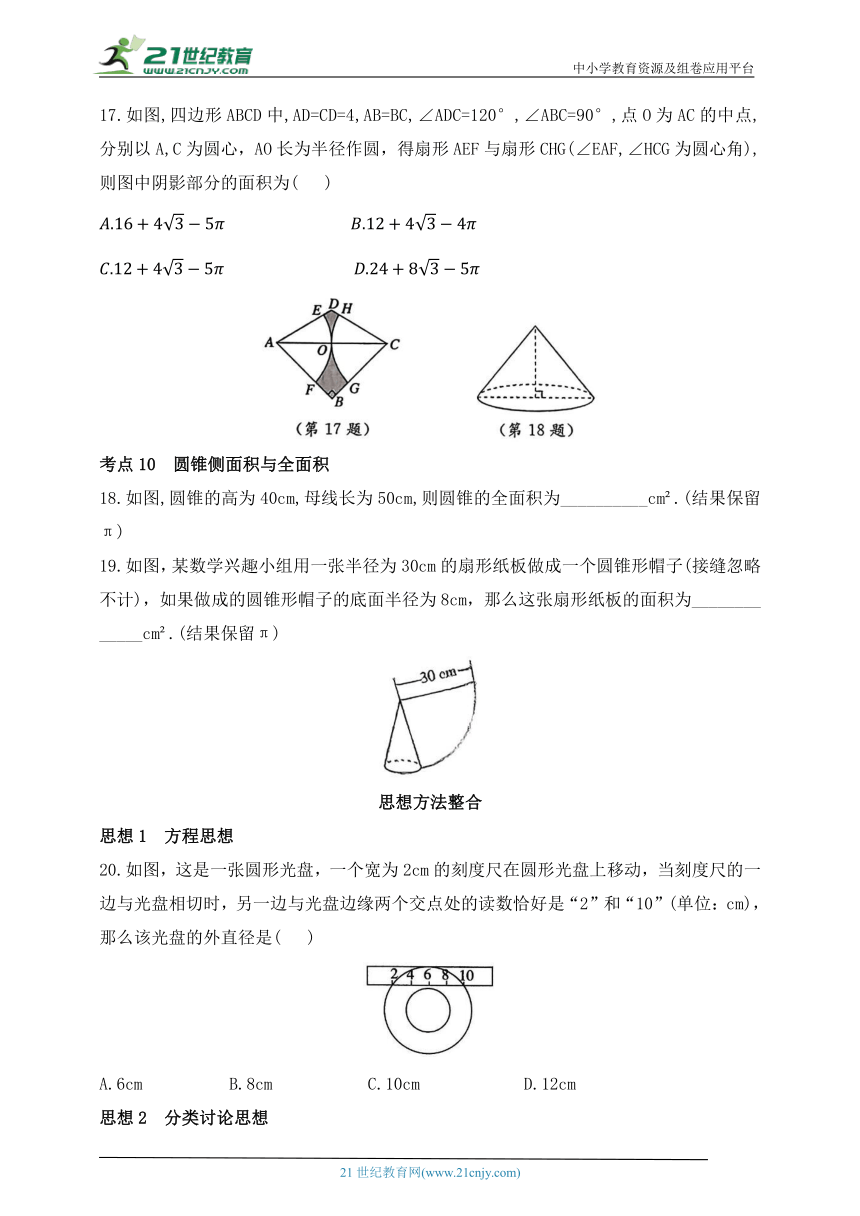
17.如图,四边形ABCD中,AD=CD=4,AB=BC,∠ADC=120°,∠ABC=90°,点O为AC的中点,分别以A,C为圆心,AO长为半径作圆,得扇形AEF与扇形CHG(∠EAF,∠HCG为圆心角),则图中阴影部分的面积为( )
考点10 圆锥侧面积与全面积
18.如图,圆锥的高为40cm,母线长为50cm,则圆锥的全面积为__________cm .(结果保留π)
19.如图,某数学兴趣小组用一张半径为30cm的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为8cm,那么这张扇形纸板的面积为_____________cm .(结果保留π)
思想方法整合
思想1 方程思想
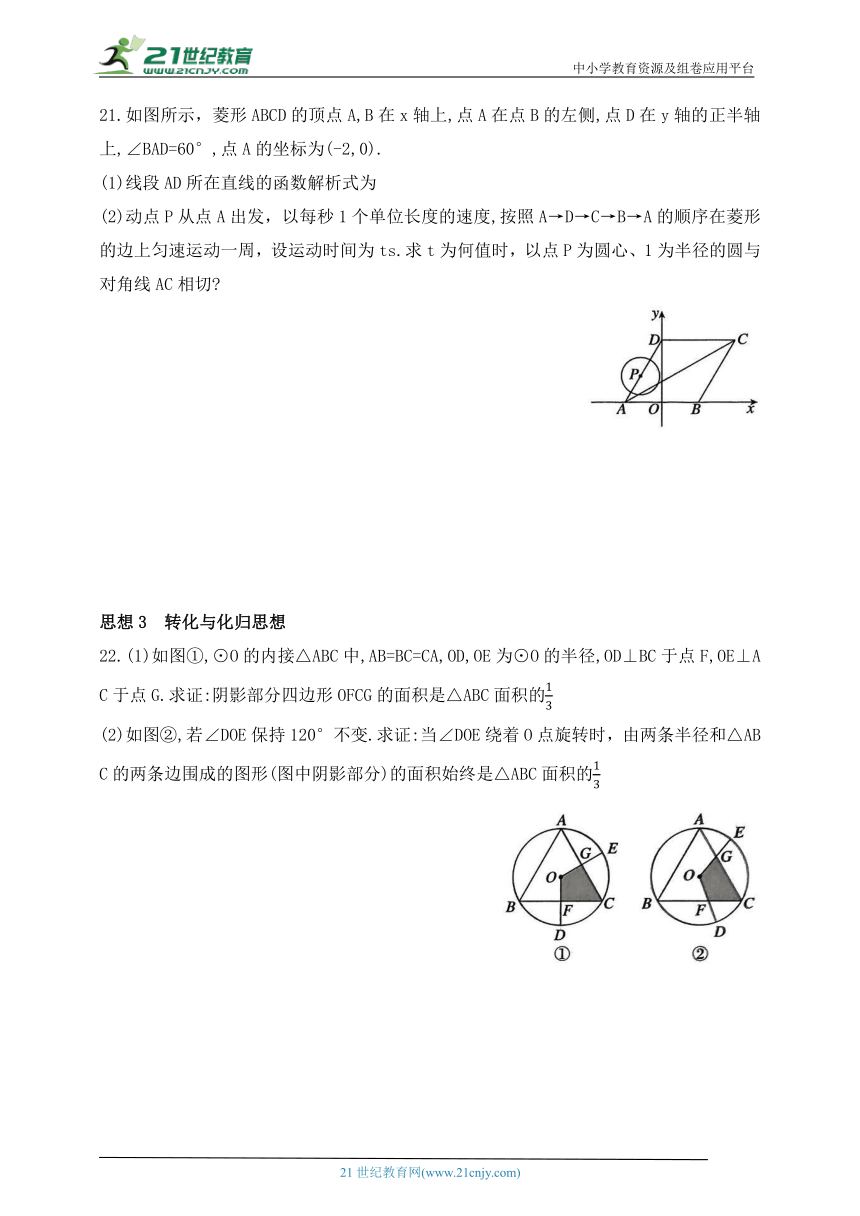
20.如图,这是一张圆形光盘,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的外直径是( )
A.6cm B.8cm C.10cm D.12cm
思想2 分类讨论思想
21.如图所示,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)线段AD所在直线的函数解析式为
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为ts.求t为何值时,以点P为圆心、1为半径的圆与对角线AC相切
思想3 转化与化归思想
22.(1)如图①,⊙O的内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.求证:阴影部分四边形OFCG的面积是△ABC面积的
(2)如图②,若∠DOE保持120°不变.求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)的面积始终是△ABC面积的
参考答案
1.B
2.D【点拨】如图,设半圆型容器的圆心为O,连接AO,过圆心O作OC⊥AB于点C,
则
在Rt△AOC中,OC=18-14=4(cm),AO=18-10=8(cm),
3.5 4.B 5.A
6.D【点拨】
∵∠BPC=70°,∴∠BDP=∠BPC-∠B=70°-20°=50°.
∵AB为⊙O的直径,∴∠ADB=90°.∴∠ADC=∠ADB-∠BDP=90°-50°=40°.
7.上
8.1≤r≤5【点拨】过点M作MH⊥AC于点H.
∵CM=2,∠ACB=30°,∴HM=CM=1.
又∵AM=5,⊙M与线段AC有交点,∴r的取值范围是1≤r≤5.
9.C【点拨】连接OC.∵OC=OB,∴∠OCB=∠OBC.
∵DE⊥AB,∴∠BDF=90°.∴∠OBC+∠DFB=90°.
∵∠EFC=∠BFD,∴∠OBC+∠EFC=90°.
∵∠ECF=∠EFC,∴∠OCB+∠ECF=90°,即OC⊥CE.
∵OC是半圆O的半径,∴CE是半圆O的切线.
10.20
11.(1)【证明】如图,连接OC.
∵OA=OC,∴∠BAC=∠OCA.∴∠DAC=∠OCA.∴OC∥AE.
∵CE⊥AD,∴OC⊥CE.
∵OC是⊙O的半径,∴CE为⊙O的切线.
(2)【解】如图,连接CB,过点C作CF⊥AB于点F.
∵∠DAC=∠CAB,CE⊥AD,∴CF=CE=2.
∵CD=BC,∴BC=CD=4.
设⊙O的半径为R,在Rt△OCF中,
解得R=4.即⊙O的半径为4.
12.B【点拨】∵⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,
∴点D,E,F分别是AB,BC,AC的中点.
∵△ABC的周长为21,即CB+CA+AB=21,∴2DF+2DE+2EF=21.
∵DE+DF=6.5,∴EF=4.
13.C【点拨】∵BC=3,AC=4,∴4-3以BC为底,高≤AC=4,∴S△ABC≤6,故B正确;
设△ABC内切圆的半径为r,
则
∵S△ABC≤6,当时,易得AB=5,∴此时r=故C错误;
当时,
∴△ABC是直角三角形,故D正确.
14.B
15.十二【点拨】如图,连接OB,OC,OD.
∵△ABC是⊙O的内接正三角形,
∵BD是⊙O的内接正四边形的一边,
∴∠COD=∠BOC-∠BOD=30°.
∴CD是⊙O的内接正十二边形的一边.
16.A【点拨】连接OE.
∵四边形ABCD是菱形,∴∠D=∠B=70°,AD=AB=3.∴OA=OD=1.5.
∵OD=OE,∴∠OED=∠D=70°.
∴DE的长
17.C【点拨】如图,连接DO.
∵AD=CD=4,∠ADC=120°,点O为AC的中点,
∴∠DAC=∠DCA=30°,AO=OC,DO⊥AC.
则
∵AB=BC,∠ABC=90°,∴∠BAC=∠BCA=45°
∴AB=BC=2,∠EAF=∠HCG=30°+45°=75°.
则
∵分别以A,C为圆心,AO长为半径作圆,得扇形AEF与扇形CHG(∠EAF,∠HCG为圆心角),
则图中阴影部分的面积为
18.2400π
19.240π【点拨】这张扇形纸板的面积240π(cm ).
20.C【点拨】设圆心为O,弦为AB,切点为C,连接OC,交AB于点D,连接OA,如图.
则AB=8cm,CD=2cm.
∵刻度尺的对边平行,光盘与直尺的外边缘相切,∴OC⊥AB.∴AD=4cm.
设光盘的外半径为Rcm,则解得R=5,
∴该光盘的外直径是10cm.
21.【解】【点拨】∵点A的坐标为(-2,0),∴OA=2.
∵∠BAD=60°,∠AOD=90°,
∴点D的坐标为(0,2).
设直线AD的函数解析式为y=kx+b,代入点A,D的坐标,
得解得
∴直线AD的函数解析式为
(2)如图所示,∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,AD=DC=CB=BA=4.
∴∠DAC=∠DCA=∠BCA=∠BAC=30°.
①当点P在AD上与AC相切时,易得
②当点P在DC上与AC相切时,易得
③当点P在BC上与AC相切时,易得
④当点P在AB上与AC相切时,易得
综上,当t的值为2或6或10或14时,以点P为圆心、1为半径的圆与对角线AC相切.
22.【证明】(1)过点O作OH⊥AB于点H.
∵AB=BC=CA,∴△ABC是等边三角形.∴∠B=∠C=60°.
∵△ABC是⊙O的内接三角形,OD⊥BC,OH⊥AB,OE⊥AC,
∴∠BHO=∠BFO=∠CFO=∠CGO=90°,BH=BF=CF=CG,OH=OF=OG.
∴四边形OFBH≌四边形OFCG.
同理得四边形OFBH≌四边形OGAH,∴四边形OFBH≌四边形OFCG≌四边形OGAH.
又∵
(2)过圆心O分别作OM⊥BC,ON⊥AC,垂足分别为M,N,
则有∠OMF=∠ONG=90°,OM=ON,∠MON=∠FOG=120°,
∴∠MON-∠FON=∠FOG-∠FON,即∠MOF=∠NOG.
∴△MOF≌△NOG.∴S△MOF=S△NOG.
∴若∠DOE保持120°不变,当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形的面积始终是△ABC面积的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
章末复习
核心考点整合
考点1 圆的有关概念
1.下列说法中,正确的是( )
A.过圆心的直线是圆的直径 B.直径是圆中最长的弦
C.相等长度的两条弧是等弧 D.顶点在圆上的角是圆周角
考点2 垂径定理及其推论
2.如图,一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图(单位:cm),则液面宽度AB=( )
3.如图,AB是⊙O的弦,OC⊥AB,垂足为C,将劣弧AB沿弦AB折叠交OC于点D,若AB=8,则⊙O的半径为______________.
考点3 弧、弦、圆心角的关系
4.如图,AB为⊙O的直径,BD=CD,∠BOD=42°,则∠AOC的度数为( )
A.90° B.96° C.98° D.100°
考点4 圆周角定理及其推论
5.如图,CD是⊙O的直径,弦DE∥AO,若则∠CDE的度数为( )
A.86° B.94° C.68° D.43°
6.如图,在⊙O中,直径AB与弦CD相交于点P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=( )
A.70° B.60° C.50° D.40°
考点5 点和圆、直线和圆的位置关系
7.在Rt△ABC中,∠C=90°,AC=2,AB=4,如果以点A为圆心,AC长为半径作⊙A,那么斜边AB的中点D在⊙A_________.(填“内”“上”或“外”)
8.如图,已知∠ACB=30°,CM=2,AM=5,以点M为圆心,r为半径作⊙M,当⊙M与线段AC有交点时,r的取值范围是______________.
考点6 切线的判定与性质
9.如图,AB是半圆O的直径,点C在半圆上(不与A,B重合),DE⊥AB于点D,交BC于点F,下列条件中能判断CE是半圆O的切线的是( )
A.∠E=∠CFE B.∠E=∠ECF C.∠ECF=∠EFC D.∠ECF=60°
10.如图,PA,PB是⊙O的切线,切点分别是A,B,点C在上,过点C的切线分别交PA,PB于点D,E.若PB=10,则△PDE的周长为_______________.
11.如图,AB为⊙O的直径,点C,D为圆上两点,连接AD,AC,CD,过点C作CE⊥AD交AD的延长线于E.
(1)求证:CE为⊙O的切线;
(2)若CD=4,CE=2求⊙O的半径.
考点7 三角形的外接圆与三角形的内切圆
12.如图,⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为( )
A.8 B.4 C.3.5 D.3
13.在△ABC中,BC=3,AC=4,下列说法错误的是( )
C.△ABC内切圆的半径 D.当时,△ABC是直角三角形
考点8 正多边形和圆
14.如图,半径为1的⊙O是正方形ABCD、正六边形DEFBGH的外接圆,则AE的长为( )
15.如图,△ABC是⊙O的内接正三角形,BD是⊙O的内接正四边形的一边,连接,则CD是⊙O的内接正_________边形的一边.
考点9 弧长与扇形面积
16.如图,在菱形ABCD中,∠B=70°,AB=3,以AD为直径的⊙O交CD于点E,则的长为( )
17.如图,四边形ABCD中,AD=CD=4,AB=BC,∠ADC=120°,∠ABC=90°,点O为AC的中点,分别以A,C为圆心,AO长为半径作圆,得扇形AEF与扇形CHG(∠EAF,∠HCG为圆心角),则图中阴影部分的面积为( )
考点10 圆锥侧面积与全面积
18.如图,圆锥的高为40cm,母线长为50cm,则圆锥的全面积为__________cm .(结果保留π)
19.如图,某数学兴趣小组用一张半径为30cm的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为8cm,那么这张扇形纸板的面积为_____________cm .(结果保留π)
思想方法整合
思想1 方程思想
20.如图,这是一张圆形光盘,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的外直径是( )
A.6cm B.8cm C.10cm D.12cm
思想2 分类讨论思想
21.如图所示,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)线段AD所在直线的函数解析式为
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为ts.求t为何值时,以点P为圆心、1为半径的圆与对角线AC相切
思想3 转化与化归思想
22.(1)如图①,⊙O的内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.求证:阴影部分四边形OFCG的面积是△ABC面积的
(2)如图②,若∠DOE保持120°不变.求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)的面积始终是△ABC面积的
参考答案
1.B
2.D【点拨】如图,设半圆型容器的圆心为O,连接AO,过圆心O作OC⊥AB于点C,
则
在Rt△AOC中,OC=18-14=4(cm),AO=18-10=8(cm),
3.5 4.B 5.A
6.D【点拨】
∵∠BPC=70°,∴∠BDP=∠BPC-∠B=70°-20°=50°.
∵AB为⊙O的直径,∴∠ADB=90°.∴∠ADC=∠ADB-∠BDP=90°-50°=40°.
7.上
8.1≤r≤5【点拨】过点M作MH⊥AC于点H.
∵CM=2,∠ACB=30°,∴HM=CM=1.
又∵AM=5,⊙M与线段AC有交点,∴r的取值范围是1≤r≤5.
9.C【点拨】连接OC.∵OC=OB,∴∠OCB=∠OBC.
∵DE⊥AB,∴∠BDF=90°.∴∠OBC+∠DFB=90°.
∵∠EFC=∠BFD,∴∠OBC+∠EFC=90°.
∵∠ECF=∠EFC,∴∠OCB+∠ECF=90°,即OC⊥CE.
∵OC是半圆O的半径,∴CE是半圆O的切线.
10.20
11.(1)【证明】如图,连接OC.
∵OA=OC,∴∠BAC=∠OCA.∴∠DAC=∠OCA.∴OC∥AE.
∵CE⊥AD,∴OC⊥CE.
∵OC是⊙O的半径,∴CE为⊙O的切线.
(2)【解】如图,连接CB,过点C作CF⊥AB于点F.
∵∠DAC=∠CAB,CE⊥AD,∴CF=CE=2.
∵CD=BC,∴BC=CD=4.
设⊙O的半径为R,在Rt△OCF中,
解得R=4.即⊙O的半径为4.
12.B【点拨】∵⊙O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,
∴点D,E,F分别是AB,BC,AC的中点.
∵△ABC的周长为21,即CB+CA+AB=21,∴2DF+2DE+2EF=21.
∵DE+DF=6.5,∴EF=4.
13.C【点拨】∵BC=3,AC=4,∴4-3
设△ABC内切圆的半径为r,
则
∵S△ABC≤6,当时,易得AB=5,∴此时r=故C错误;
当时,
∴△ABC是直角三角形,故D正确.
14.B
15.十二【点拨】如图,连接OB,OC,OD.
∵△ABC是⊙O的内接正三角形,
∵BD是⊙O的内接正四边形的一边,
∴∠COD=∠BOC-∠BOD=30°.
∴CD是⊙O的内接正十二边形的一边.
16.A【点拨】连接OE.
∵四边形ABCD是菱形,∴∠D=∠B=70°,AD=AB=3.∴OA=OD=1.5.
∵OD=OE,∴∠OED=∠D=70°.
∴DE的长
17.C【点拨】如图,连接DO.
∵AD=CD=4,∠ADC=120°,点O为AC的中点,
∴∠DAC=∠DCA=30°,AO=OC,DO⊥AC.
则
∵AB=BC,∠ABC=90°,∴∠BAC=∠BCA=45°
∴AB=BC=2,∠EAF=∠HCG=30°+45°=75°.
则
∵分别以A,C为圆心,AO长为半径作圆,得扇形AEF与扇形CHG(∠EAF,∠HCG为圆心角),
则图中阴影部分的面积为
18.2400π
19.240π【点拨】这张扇形纸板的面积240π(cm ).
20.C【点拨】设圆心为O,弦为AB,切点为C,连接OC,交AB于点D,连接OA,如图.
则AB=8cm,CD=2cm.
∵刻度尺的对边平行,光盘与直尺的外边缘相切,∴OC⊥AB.∴AD=4cm.
设光盘的外半径为Rcm,则解得R=5,
∴该光盘的外直径是10cm.
21.【解】【点拨】∵点A的坐标为(-2,0),∴OA=2.
∵∠BAD=60°,∠AOD=90°,
∴点D的坐标为(0,2).
设直线AD的函数解析式为y=kx+b,代入点A,D的坐标,
得解得
∴直线AD的函数解析式为
(2)如图所示,∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,AD=DC=CB=BA=4.
∴∠DAC=∠DCA=∠BCA=∠BAC=30°.
①当点P在AD上与AC相切时,易得
②当点P在DC上与AC相切时,易得
③当点P在BC上与AC相切时,易得
④当点P在AB上与AC相切时,易得
综上,当t的值为2或6或10或14时,以点P为圆心、1为半径的圆与对角线AC相切.
22.【证明】(1)过点O作OH⊥AB于点H.
∵AB=BC=CA,∴△ABC是等边三角形.∴∠B=∠C=60°.
∵△ABC是⊙O的内接三角形,OD⊥BC,OH⊥AB,OE⊥AC,
∴∠BHO=∠BFO=∠CFO=∠CGO=90°,BH=BF=CF=CG,OH=OF=OG.
∴四边形OFBH≌四边形OFCG.
同理得四边形OFBH≌四边形OGAH,∴四边形OFBH≌四边形OFCG≌四边形OGAH.
又∵
(2)过圆心O分别作OM⊥BC,ON⊥AC,垂足分别为M,N,
则有∠OMF=∠ONG=90°,OM=ON,∠MON=∠FOG=120°,
∴∠MON-∠FON=∠FOG-∠FON,即∠MOF=∠NOG.
∴△MOF≌△NOG.∴S△MOF=S△NOG.
∴若∠DOE保持120°不变,当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形的面积始终是△ABC面积的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
