第二十四章 圆 专题 构造圆的基本图形的八大技法(含答案)
文档属性
| 名称 | 第二十四章 圆 专题 构造圆的基本图形的八大技法(含答案) | 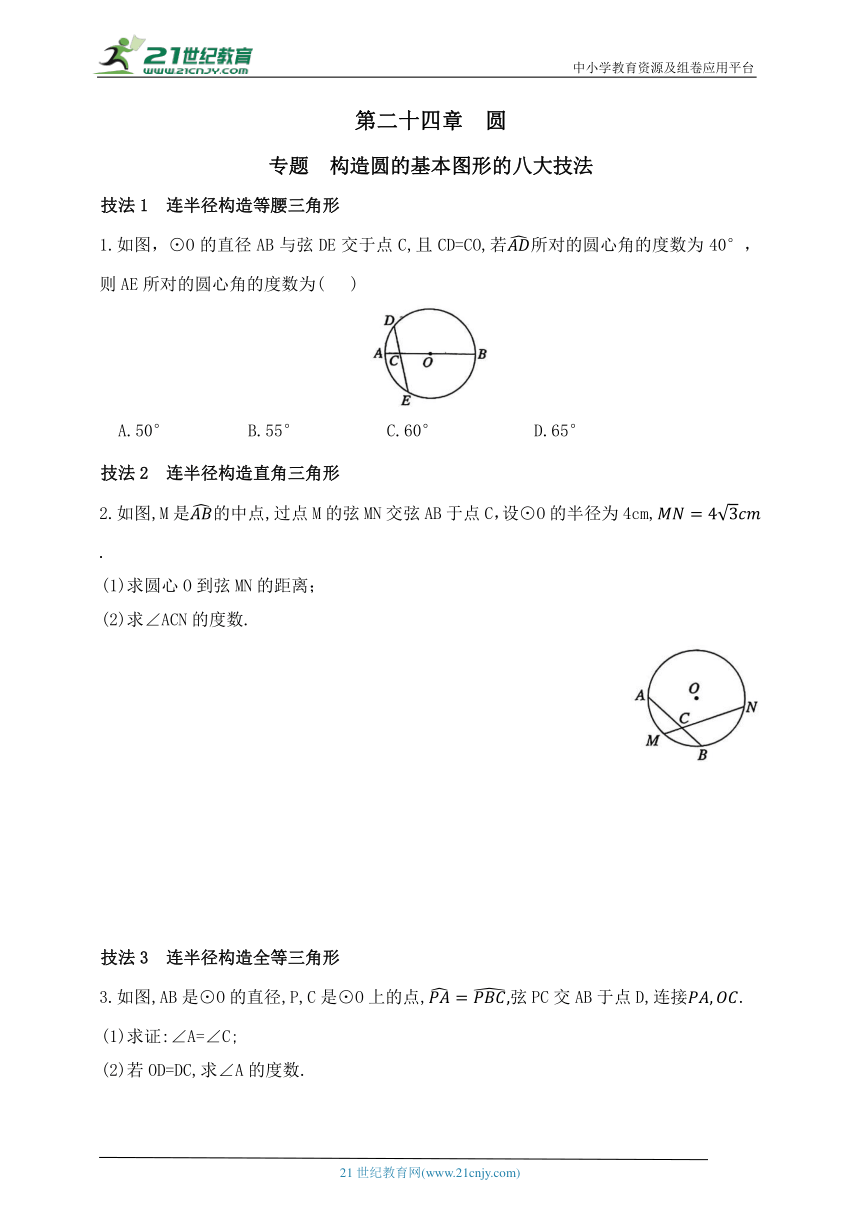 | |
| 格式 | docx | ||
| 文件大小 | 388.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:38:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
专题 构造圆的基本图形的八大技法
技法1 连半径构造等腰三角形
1.如图,⊙O的直径AB与弦DE交于点C,且CD=CO,若所对的圆心角的度数为40°,则AE所对的圆心角的度数为( )
A.50° B.55° C.60° D.65°
技法2 连半径构造直角三角形
2.如图,M是的中点,过点M的弦MN交弦AB于点C,设⊙O的半径为4cm,
(1)求圆心O到弦MN的距离;
(2)求∠ACN的度数.
技法3 连半径构造全等三角形
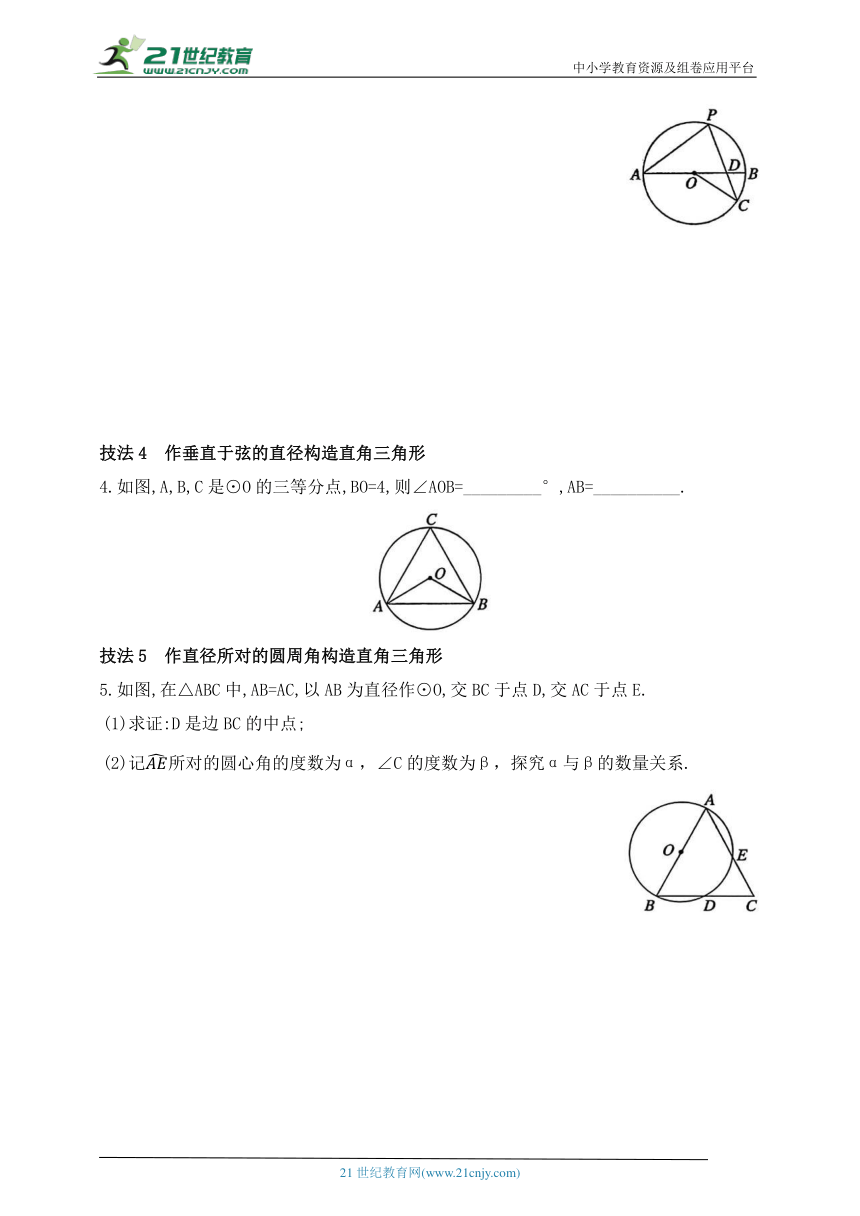
3.如图,AB是⊙O的直径,P,C是⊙O上的点,弦PC交AB于点D,连接.
(1)求证:∠A=∠C;
(2)若OD=DC,求∠A的度数.
技法4 作垂直于弦的直径构造直角三角形
4.如图,A,B,C是⊙O的三等分点,BO=4,则∠AOB=_________°,AB=__________.
技法5 作直径所对的圆周角构造直角三角形
5.如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交AC于点E.
(1)求证:D是边BC的中点;
(2)记所对的圆心角的度数为α,∠C的度数为β,探究α与β的数量关系.
技法6 作直角所对弦(直径)构造直角三角形
6.如图,四边形ABCD为矩形,AB=8,AD=12.P是线段AD上一动点,点E为线段BP上一点,连接AE,CE,∠BCE=∠ABP,则AE的最小值为( )
A.4 B.5 C.6 D.8
技法7 截长法构造全等三角形
7.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦弦BM平分交AC于点D,连接MA,MC.
(1)求⊙O的半径长;
(2)求证:AB+BC=BM.
技法8 补形法构造全等三角形
8.如图,BC是半圆O的直径,P是半圆的中点,A是BP的中点,AD⊥BC于点D,连接AB,PB,AC,BP分别与AD,AC相交于点E,F.
(1)求证:AE=BE.
(2)判断BE与EF是否相等,请说明理由.
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确 若正确,请说明理由;若不正确,请写出CF与AB之间正确的关系式.
参考答案
1.C
2.【解】(1)如图,过点O作OD⊥MN,垂足为D,连接OM,∴MD=ND.
又∵OM=4cm,
即圆心O到弦MN的距离为2cm.
(2)∵M是AB的中点,∴OM⊥AB.
由(1)易得∠OMD=30°.∴∠ACM=60°.∴∠ACN=120°.
3.(1)【证明】如图,连接OP.
在△POA和△POC中,∴△POA≌△POC(SSS).∴∠A=∠C.
(2)【解】设∠A=∠C=a°,∵OA=OP:∴∠A=∠OPA=x°;∴∠FOB=2∠A=2x°,
∵OD=DC,∴∠DOC=∠C==;
∵OP=OC,∴∠OPC=∠C=4°.
在△POC中,x+x+2x+x=180,解得x=36,∴∠A=36°,
4.120;4【点拨】∵A,B,C是⊙O的三等分点,∴AB=BC=AC,∴AB=BC=AC,
∴△ABC为等边三角形.∴∠ACB=60°,∴∠AOB=2∠ACB=120°,
如图,过点O作OD⊥AB于点D,
∴
∴在Rt△BOD中,
5.(1)【证明】如图,连接AD,
∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,
∵AB=AC,∴BD=CD,即D是边BC的中点.
(2)【解理由如下:如图,连接OE,
所对的圆心角的度数为a,∴∠AOE=a.
∵OA=OE,
∵AB=AC,∴∠ABC=∠C=β∴∠BAC=180°=2∠C=180°-2A
脚
6.A【点拨】∵四边形ABCD为矩形、∴∠ABP=∠CBP=∠ABC=90°.又∵∠BCE=∠ABP、∴∠BCE+∠CDP=90°.∴∠BEC=90°.∴点E在以BC的中点O为横心、OB长为半径的圆弧上运动.如图所示、连接OA交隔弧于点E,此时AE有最小值,
∵AD=BC=12、
又∵AB=8
∴AE=AO-OE=10-6=4,即AE的最小值为%.
7.(1)【解】如图,连接OA,OC、作OH⊥AC于点H.
∵∠ABC=120°,∴∠AOC=2∠AMC=120°.
易知
又∵OH⊥AC,∴∠OAH=30°.
在Rt△AOH中,(即
解得OA=2(负值已舍去),即⊙O的半径长为2.
(2)【证明】如图,在BM上截取BE=BC,连接CE.
∵BM平分∠ABC,∠ABC=120°,
又∵BE=BC,∴△EBC是等边三角形.∴CE=CB=BE,∠CEB=60°.
.
又∵∠CMB=∠CAB,∴△ABC≌△MEC(AAS).∴AB=ME.
∵ME+EB=BM,∴AB+BC=BM.
8.(1)【证明】∵BC是半圆O的直径,∴∠BAC=90°.∴∠ACB+∠ABC=90°.
∵AD⊥BC,∴∠ADB=90°.∴∠BAD+∠ABD=90°.∴∠ACB=∠BAD.
∵A是BP的中点,∴AB=AP.∴∠ACB=∠ABP.∴∠ABE=∠BAE.∴AE=BE.
(2)【解】BE=EF.理由如下:
由(1)知∠BAC=90°,∴∠BAE+∠FAD=∠ABF+∠AFB=90°.
又∵∠BAE=∠ABF,∴∠FAD=∠AFB.∴EF=AE.
又∵AE=BE,∴BE=EF.
(3)【解】小李的发现是正确的.
理由如下:如图,连接CP,延长BA与CP交于点G.
∵P为半圆O的中点,∴BP=PC.
∵BC是半圆O的直径,∴∠CPF=∠BPG=90°.
又∵∠PCF=∠PBG,∴△PCF≌△PBG(ASA).∴CF=BG.
∵BC为半圆O的直径,∴∠BAC=∠GAC=90°.
∵AB=AP,∴∠GCA=∠BCA.
又∵CA=CA,∴△BAC≌△GAC(ASA).∴CF=BG=2AB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
专题 构造圆的基本图形的八大技法
技法1 连半径构造等腰三角形
1.如图,⊙O的直径AB与弦DE交于点C,且CD=CO,若所对的圆心角的度数为40°,则AE所对的圆心角的度数为( )
A.50° B.55° C.60° D.65°
技法2 连半径构造直角三角形
2.如图,M是的中点,过点M的弦MN交弦AB于点C,设⊙O的半径为4cm,
(1)求圆心O到弦MN的距离;
(2)求∠ACN的度数.
技法3 连半径构造全等三角形
3.如图,AB是⊙O的直径,P,C是⊙O上的点,弦PC交AB于点D,连接.
(1)求证:∠A=∠C;
(2)若OD=DC,求∠A的度数.
技法4 作垂直于弦的直径构造直角三角形
4.如图,A,B,C是⊙O的三等分点,BO=4,则∠AOB=_________°,AB=__________.
技法5 作直径所对的圆周角构造直角三角形
5.如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交AC于点E.
(1)求证:D是边BC的中点;
(2)记所对的圆心角的度数为α,∠C的度数为β,探究α与β的数量关系.
技法6 作直角所对弦(直径)构造直角三角形
6.如图,四边形ABCD为矩形,AB=8,AD=12.P是线段AD上一动点,点E为线段BP上一点,连接AE,CE,∠BCE=∠ABP,则AE的最小值为( )
A.4 B.5 C.6 D.8
技法7 截长法构造全等三角形
7.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦弦BM平分交AC于点D,连接MA,MC.
(1)求⊙O的半径长;
(2)求证:AB+BC=BM.
技法8 补形法构造全等三角形
8.如图,BC是半圆O的直径,P是半圆的中点,A是BP的中点,AD⊥BC于点D,连接AB,PB,AC,BP分别与AD,AC相交于点E,F.
(1)求证:AE=BE.
(2)判断BE与EF是否相等,请说明理由.
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确 若正确,请说明理由;若不正确,请写出CF与AB之间正确的关系式.
参考答案
1.C
2.【解】(1)如图,过点O作OD⊥MN,垂足为D,连接OM,∴MD=ND.
又∵OM=4cm,
即圆心O到弦MN的距离为2cm.
(2)∵M是AB的中点,∴OM⊥AB.
由(1)易得∠OMD=30°.∴∠ACM=60°.∴∠ACN=120°.
3.(1)【证明】如图,连接OP.
在△POA和△POC中,∴△POA≌△POC(SSS).∴∠A=∠C.
(2)【解】设∠A=∠C=a°,∵OA=OP:∴∠A=∠OPA=x°;∴∠FOB=2∠A=2x°,
∵OD=DC,∴∠DOC=∠C==;
∵OP=OC,∴∠OPC=∠C=4°.
在△POC中,x+x+2x+x=180,解得x=36,∴∠A=36°,
4.120;4【点拨】∵A,B,C是⊙O的三等分点,∴AB=BC=AC,∴AB=BC=AC,
∴△ABC为等边三角形.∴∠ACB=60°,∴∠AOB=2∠ACB=120°,
如图,过点O作OD⊥AB于点D,
∴
∴在Rt△BOD中,
5.(1)【证明】如图,连接AD,
∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,
∵AB=AC,∴BD=CD,即D是边BC的中点.
(2)【解理由如下:如图,连接OE,
所对的圆心角的度数为a,∴∠AOE=a.
∵OA=OE,
∵AB=AC,∴∠ABC=∠C=β∴∠BAC=180°=2∠C=180°-2A
脚
6.A【点拨】∵四边形ABCD为矩形、∴∠ABP=∠CBP=∠ABC=90°.又∵∠BCE=∠ABP、∴∠BCE+∠CDP=90°.∴∠BEC=90°.∴点E在以BC的中点O为横心、OB长为半径的圆弧上运动.如图所示、连接OA交隔弧于点E,此时AE有最小值,
∵AD=BC=12、
又∵AB=8
∴AE=AO-OE=10-6=4,即AE的最小值为%.
7.(1)【解】如图,连接OA,OC、作OH⊥AC于点H.
∵∠ABC=120°,∴∠AOC=2∠AMC=120°.
易知
又∵OH⊥AC,∴∠OAH=30°.
在Rt△AOH中,(即
解得OA=2(负值已舍去),即⊙O的半径长为2.
(2)【证明】如图,在BM上截取BE=BC,连接CE.
∵BM平分∠ABC,∠ABC=120°,
又∵BE=BC,∴△EBC是等边三角形.∴CE=CB=BE,∠CEB=60°.
.
又∵∠CMB=∠CAB,∴△ABC≌△MEC(AAS).∴AB=ME.
∵ME+EB=BM,∴AB+BC=BM.
8.(1)【证明】∵BC是半圆O的直径,∴∠BAC=90°.∴∠ACB+∠ABC=90°.
∵AD⊥BC,∴∠ADB=90°.∴∠BAD+∠ABD=90°.∴∠ACB=∠BAD.
∵A是BP的中点,∴AB=AP.∴∠ACB=∠ABP.∴∠ABE=∠BAE.∴AE=BE.
(2)【解】BE=EF.理由如下:
由(1)知∠BAC=90°,∴∠BAE+∠FAD=∠ABF+∠AFB=90°.
又∵∠BAE=∠ABF,∴∠FAD=∠AFB.∴EF=AE.
又∵AE=BE,∴BE=EF.
(3)【解】小李的发现是正确的.
理由如下:如图,连接CP,延长BA与CP交于点G.
∵P为半圆O的中点,∴BP=PC.
∵BC是半圆O的直径,∴∠CPF=∠BPG=90°.
又∵∠PCF=∠PBG,∴△PCF≌△PBG(ASA).∴CF=BG.
∵BC为半圆O的直径,∴∠BAC=∠GAC=90°.
∵AB=AP,∴∠GCA=∠BCA.
又∵CA=CA,∴△BAC≌△GAC(ASA).∴CF=BG=2AB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
