第二十四章 圆 专题 圆中常见的计算题型(含答案)
文档属性
| 名称 | 第二十四章 圆 专题 圆中常见的计算题型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 459.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 12:51:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
专题 圆中常见的计算题型
类型1 与圆有关的线段长的计算
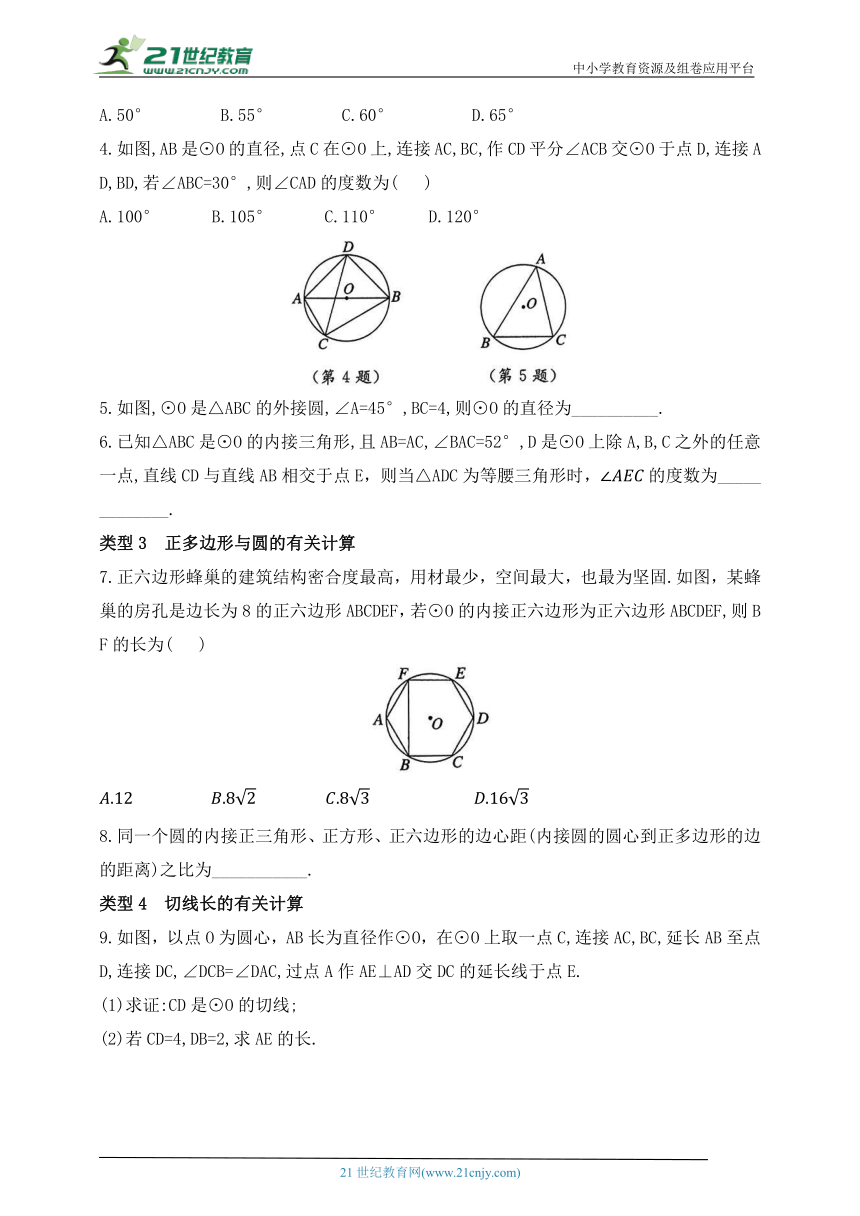
1.如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A,B,作半径OC⊥弦AB交外圆于点C,交内圆于点D.测得CD=10cm,AB=60cm,则这个车轮的外圆半径长是____________.
2.在⊙O中,直径AB=6,BC是⊙O的弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图①,当PQ∥AB时,求PQ的长;
(2)如图②,当点P在BC上移动时,求PQ长的最大值.
类型2 与圆有关的角的计算
3.如图,四边形ABCD内接于⊙O,连接OB,OD,E为BC延长线上一点.若∠BOD=100°,则∠ECD的度数是( )
A.50° B.55° C.60° D.65°
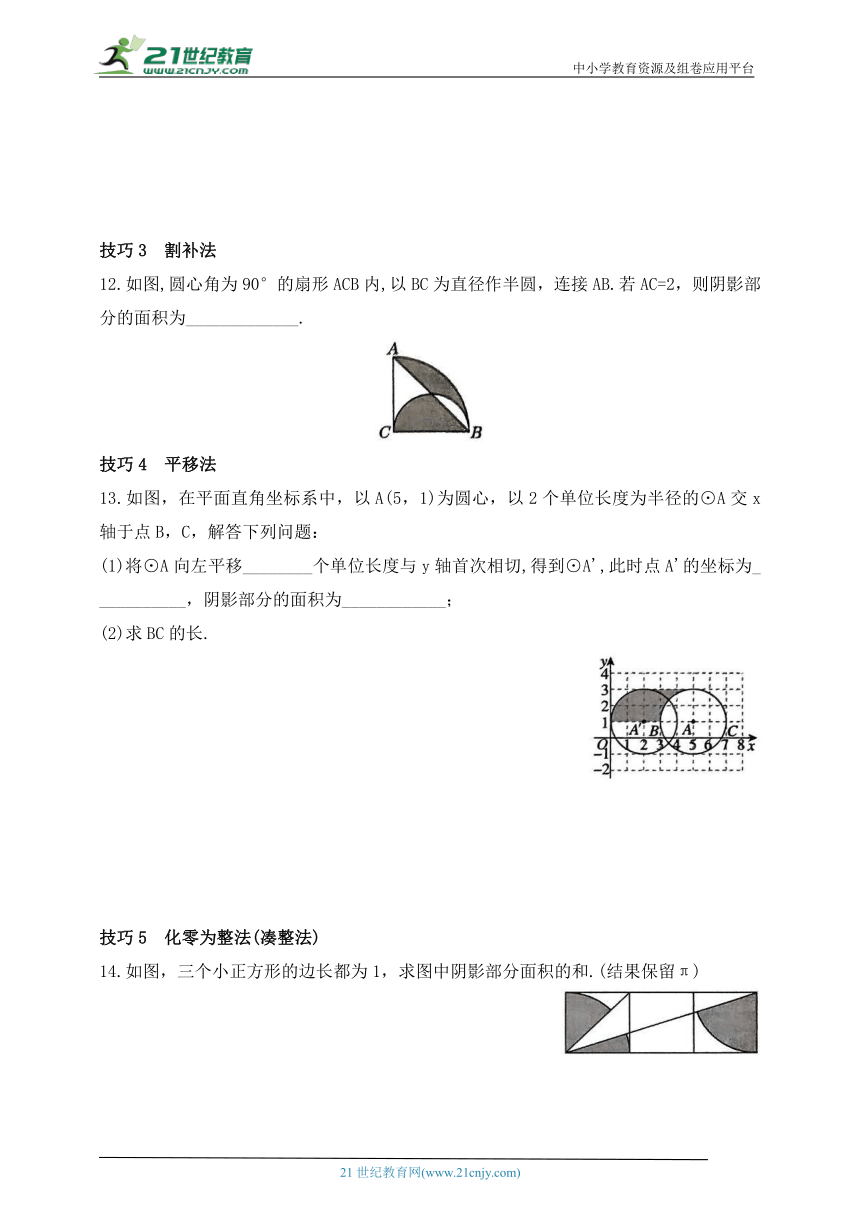
4.如图,AB是⊙O的直径,点C在⊙O上,连接AC,BC,作CD平分∠ACB交⊙O于点D,连接AD,BD,若∠ABC=30°,则∠CAD的度数为( )
A.100° B.105° C.110° D.120°
5.如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为__________.
6.已知△ABC是⊙O的内接三角形,且AB=AC,∠BAC=52°,D是⊙O上除A,B,C之外的任意一点,直线CD与直线AB相交于点E,则当△ADC为等腰三角形时,的度数为_____________.
类型3 正多边形与圆的有关计算
7.正六边形蜂巢的建筑结构密合度最高,用材最少,空间最大,也最为坚固.如图,某蜂巢的房孔是边长为8的正六边形ABCDEF,若⊙O的内接正六边形为正六边形ABCDEF,则BF的长为( )
8.同一个圆的内接正三角形、正方形、正六边形的边心距(内接圆的圆心到正多边形的边的距离)之比为___________.
类型4 切线长的有关计算
9.如图,以点O为圆心,AB长为直径作⊙O,在⊙O上取一点C,连接AC,BC,延长AB至点D,连接DC,∠DCB=∠DAC,过点A作AE⊥AD交DC的延长线于点E.
(1)求证:CD是⊙O的切线;
(2)若CD=4,DB=2,求AE的长.
类型5 阴影部分面积的计算
技巧1 和差法
10.如图,矩形ABCD内接于⊙O,分别以AB,BC,CD,AD为直径向外作半圆.若AB=4,BC=5,则阴影部分的面积是( )
技巧2 等积法
11.如图,AB为⊙O的直径,射线AD交⊙O于点F,C为BF的中点,过点C作CE⊥AD,垂足为E,连接AC.
(1)求证:CE是⊙O的切线;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
技巧3 割补法
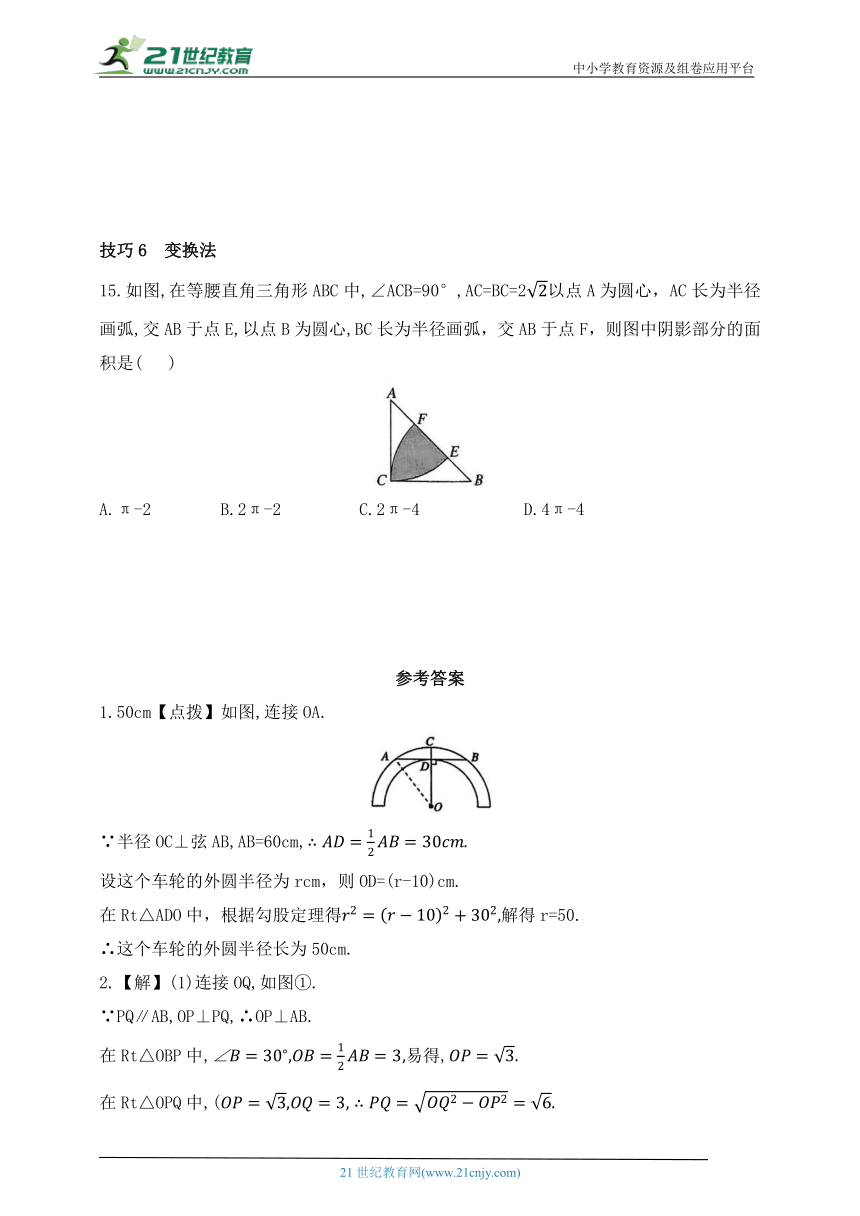
12.如图,圆心角为90°的扇形ACB内,以BC为直径作半圆,连接AB.若AC=2,则阴影部分的面积为_____________.
技巧4 平移法
13.如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B,C,解答下列问题:
(1)将⊙A向左平移________个单位长度与y轴首次相切,得到⊙A',此时点A'的坐标为___________,阴影部分的面积为____________;
(2)求BC的长.
技巧5 化零为整法(凑整法)
14.如图,三个小正方形的边长都为1,求图中阴影部分面积的和.(结果保留π)
技巧6 变换法
15.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=2以点A为圆心,AC长为半径画弧,交AB于点E,以点B为圆心,BC长为半径画弧,交AB于点F,则图中阴影部分的面积是( )
A.π-2 B.2π-2 C.2π-4 D.4π-4
参考答案
1.50cm【点拨】如图,连接OA.
∵半径OC⊥弦AB,AB=60cm,
设这个车轮的外圆半径为rcm,则OD=(r-10)cm.
在Rt△ADO中,根据勾股定理得解得r=50.
∴这个车轮的外圆半径长为50cm.
2.【解】(1)连接OQ,如图①.
∵PQ∥AB,OP⊥PQ,∴OP⊥AB.
在Rt△OBP中,易得,
在Rt△OPQ中,(
(2)连接OQ,如图②.
在Rt△OPQ中,
则当OP的长最小时,PQ的长有最大值.
当OP⊥BC时,OP的长最小,此时易得
∴PQ长的最大值为
③点方法圆中与弦有关的计算或证明问题,往往需要连接半径,以构造直角三角形,从而应用勾股定理进行计算,
3.A
4.B【点拨】∵AB是⊙O的直径,∴∠ACB=90°,
又∵∠ABC=30°,∴∠BAC=90°-∠ABC=90°-30°=60°,
∵CD平分∠ACB,∴∠BCD=45°.∴∠BAD=∠BCD=45°.
∴∠CAD=∠BAC+∠BAD=60°+45°=105°.
5.4
6.70°或76°或20°【点拨】∵AB=AC,∠BAC=52°,
若△ADC为等腰三角形,则需分以下情况讨论:
①如图①,当AD=CD时,∠DAC=∠DCA.
∵∠D=∠B=64°,
∴∠BCD=∠ACB-∠ACD=64°-58°=6°.∴∠AEC=∠B+∠BCD=64°+6°=70°;
②如图②,当CD=CA时,∠CDA=∠CAD.
∵∠D=∠B=64°,∴∠CAD=64°.∴∠BAD=∠CAD-∠BAC=64°-52°=12°.
∴∠AEC=∠D+∠BAD=64°+12°=76°;
③如图③,当AD=CD时,∠DAC=∠DCA.
∵∠B=64°,∴∠ADC=180°-∠B=116°.
∴∠DAE=180°-∠BAC-∠DAC=180°-52°-32°=96°.
∴∠AEC=∠ADC-∠DAE=116°-96°=20°.
综上,当△ADC为等腰三角形时,∠AEC的度数为70°或76°或20°,
7.C 8.1::
9.(1)【证明】如图,连接OC.
∵AB为⊙O直径,∴∠ACB=90°,即∠BCO+∠OCA=90°.
∵OC=OA,∴∠OCA=∠OAC.
又∵∠DCB=∠DAC,∴∠OCA=∠DCB.
∴∠DCB+∠BCO=90°,即∠DCO=90°,∴OC⊥DC.
又∵OC是⊙O的半径,∴CD是⊙O的切线.
(2)【解】
又∵OC=OB,CD=4,DB=2,∴OB +4 =(OB+2) .∴OB=3.∴AB=6.
∵AE⊥AD,AB是⊙O的直径,∴AE是⊙O的切线.
又∵CD是⊙O的切线,∴AE=CE.
∵.AE=6.
10.D【点拨】如图,连接BD,则BD过圆心O.
在矩形ABCD中,AB=CD=4,AD=BC=5,∠A=90°,
∴S阴影=S以AD为直径的圆+S以AB为直径的圆+S矩形ABCD-S⊙O
=20.
11(1)【证明】如图,连接BF,OC.
∵AB是⊙O的直径,∴∠AFB=90°,即BF⊥AD.
又∵CE⊥AD,∴BF∥CE.
∵C为BF的中点,∴OC⊥BF.
∵BF∥CE,∴OC⊥CE.
又∵OC是⊙O的半径,∴CE是⊙O的切线.
(2)【解】如图,连接OF与AC交于点M.
∵OA=OC,∠BAC=30°,∴∠BAC=∠ACO=30°.∴∠BOC=60°.
∵AD⊥CE,由(1)知OC⊥CE,∴AD∥OC.∴∠FAM=∠OCM=30°,∠FAB=∠BOC=60°.
又∵OA=OF,∴△AFO为等边三角形.∴AF=OA=OC.
又∵∠FMA=∠OMC,∴△AFM≌△COM.∴∴
∵C为的中点,∴∠FOC=∠BOC=60°.
∵AB=4,∴FO=OC=OB=2.即阴影部分的面积为π.
12.π-1【点拨】如图,设以BC为直径的半圆与AB交于点D,连接CD.
在Rt△ACB中,AC=BC=2,
∵BC是半圆的直径,∴∠CDB=90°,即CD⊥AB.
又∵CA=CB,∴CD=BD=AD=.
易知D为的中点,
∴
点方法 计算不规则图形的面积时,常常通过割补法将不,图形的面积转化为几个规则图形面积的和或差.
13.【解】(1)3;(2,1);6
(2)如图,连接AC,过点A作AD⊥BC于点D,则BC=2DC.
∵⊙A的半径AC=2,由A(5,1)可得AD=1,
∴在Rt△ADC中,
14.【解】易知,三个扇形的半径都为1,三个扇形圆心角的度数和为∴阴影部分面积的和为
点方法 利用凑整法可将图中阴影部分拼成一个圆心角为135°、半径是1的扇形,
15.C【点拨】在等腰直角三角形ABC中,∠ACB=90°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
专题 圆中常见的计算题型
类型1 与圆有关的线段长的计算
1.如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A,B,作半径OC⊥弦AB交外圆于点C,交内圆于点D.测得CD=10cm,AB=60cm,则这个车轮的外圆半径长是____________.
2.在⊙O中,直径AB=6,BC是⊙O的弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图①,当PQ∥AB时,求PQ的长;
(2)如图②,当点P在BC上移动时,求PQ长的最大值.
类型2 与圆有关的角的计算
3.如图,四边形ABCD内接于⊙O,连接OB,OD,E为BC延长线上一点.若∠BOD=100°,则∠ECD的度数是( )
A.50° B.55° C.60° D.65°
4.如图,AB是⊙O的直径,点C在⊙O上,连接AC,BC,作CD平分∠ACB交⊙O于点D,连接AD,BD,若∠ABC=30°,则∠CAD的度数为( )
A.100° B.105° C.110° D.120°
5.如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为__________.
6.已知△ABC是⊙O的内接三角形,且AB=AC,∠BAC=52°,D是⊙O上除A,B,C之外的任意一点,直线CD与直线AB相交于点E,则当△ADC为等腰三角形时,的度数为_____________.
类型3 正多边形与圆的有关计算
7.正六边形蜂巢的建筑结构密合度最高,用材最少,空间最大,也最为坚固.如图,某蜂巢的房孔是边长为8的正六边形ABCDEF,若⊙O的内接正六边形为正六边形ABCDEF,则BF的长为( )
8.同一个圆的内接正三角形、正方形、正六边形的边心距(内接圆的圆心到正多边形的边的距离)之比为___________.
类型4 切线长的有关计算
9.如图,以点O为圆心,AB长为直径作⊙O,在⊙O上取一点C,连接AC,BC,延长AB至点D,连接DC,∠DCB=∠DAC,过点A作AE⊥AD交DC的延长线于点E.
(1)求证:CD是⊙O的切线;
(2)若CD=4,DB=2,求AE的长.
类型5 阴影部分面积的计算
技巧1 和差法
10.如图,矩形ABCD内接于⊙O,分别以AB,BC,CD,AD为直径向外作半圆.若AB=4,BC=5,则阴影部分的面积是( )
技巧2 等积法
11.如图,AB为⊙O的直径,射线AD交⊙O于点F,C为BF的中点,过点C作CE⊥AD,垂足为E,连接AC.
(1)求证:CE是⊙O的切线;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
技巧3 割补法
12.如图,圆心角为90°的扇形ACB内,以BC为直径作半圆,连接AB.若AC=2,则阴影部分的面积为_____________.
技巧4 平移法
13.如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B,C,解答下列问题:
(1)将⊙A向左平移________个单位长度与y轴首次相切,得到⊙A',此时点A'的坐标为___________,阴影部分的面积为____________;
(2)求BC的长.
技巧5 化零为整法(凑整法)
14.如图,三个小正方形的边长都为1,求图中阴影部分面积的和.(结果保留π)
技巧6 变换法
15.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=2以点A为圆心,AC长为半径画弧,交AB于点E,以点B为圆心,BC长为半径画弧,交AB于点F,则图中阴影部分的面积是( )
A.π-2 B.2π-2 C.2π-4 D.4π-4
参考答案
1.50cm【点拨】如图,连接OA.
∵半径OC⊥弦AB,AB=60cm,
设这个车轮的外圆半径为rcm,则OD=(r-10)cm.
在Rt△ADO中,根据勾股定理得解得r=50.
∴这个车轮的外圆半径长为50cm.
2.【解】(1)连接OQ,如图①.
∵PQ∥AB,OP⊥PQ,∴OP⊥AB.
在Rt△OBP中,易得,
在Rt△OPQ中,(
(2)连接OQ,如图②.
在Rt△OPQ中,
则当OP的长最小时,PQ的长有最大值.
当OP⊥BC时,OP的长最小,此时易得
∴PQ长的最大值为
③点方法圆中与弦有关的计算或证明问题,往往需要连接半径,以构造直角三角形,从而应用勾股定理进行计算,
3.A
4.B【点拨】∵AB是⊙O的直径,∴∠ACB=90°,
又∵∠ABC=30°,∴∠BAC=90°-∠ABC=90°-30°=60°,
∵CD平分∠ACB,∴∠BCD=45°.∴∠BAD=∠BCD=45°.
∴∠CAD=∠BAC+∠BAD=60°+45°=105°.
5.4
6.70°或76°或20°【点拨】∵AB=AC,∠BAC=52°,
若△ADC为等腰三角形,则需分以下情况讨论:
①如图①,当AD=CD时,∠DAC=∠DCA.
∵∠D=∠B=64°,
∴∠BCD=∠ACB-∠ACD=64°-58°=6°.∴∠AEC=∠B+∠BCD=64°+6°=70°;
②如图②,当CD=CA时,∠CDA=∠CAD.
∵∠D=∠B=64°,∴∠CAD=64°.∴∠BAD=∠CAD-∠BAC=64°-52°=12°.
∴∠AEC=∠D+∠BAD=64°+12°=76°;
③如图③,当AD=CD时,∠DAC=∠DCA.
∵∠B=64°,∴∠ADC=180°-∠B=116°.
∴∠DAE=180°-∠BAC-∠DAC=180°-52°-32°=96°.
∴∠AEC=∠ADC-∠DAE=116°-96°=20°.
综上,当△ADC为等腰三角形时,∠AEC的度数为70°或76°或20°,
7.C 8.1::
9.(1)【证明】如图,连接OC.
∵AB为⊙O直径,∴∠ACB=90°,即∠BCO+∠OCA=90°.
∵OC=OA,∴∠OCA=∠OAC.
又∵∠DCB=∠DAC,∴∠OCA=∠DCB.
∴∠DCB+∠BCO=90°,即∠DCO=90°,∴OC⊥DC.
又∵OC是⊙O的半径,∴CD是⊙O的切线.
(2)【解】
又∵OC=OB,CD=4,DB=2,∴OB +4 =(OB+2) .∴OB=3.∴AB=6.
∵AE⊥AD,AB是⊙O的直径,∴AE是⊙O的切线.
又∵CD是⊙O的切线,∴AE=CE.
∵.AE=6.
10.D【点拨】如图,连接BD,则BD过圆心O.
在矩形ABCD中,AB=CD=4,AD=BC=5,∠A=90°,
∴S阴影=S以AD为直径的圆+S以AB为直径的圆+S矩形ABCD-S⊙O
=20.
11(1)【证明】如图,连接BF,OC.
∵AB是⊙O的直径,∴∠AFB=90°,即BF⊥AD.
又∵CE⊥AD,∴BF∥CE.
∵C为BF的中点,∴OC⊥BF.
∵BF∥CE,∴OC⊥CE.
又∵OC是⊙O的半径,∴CE是⊙O的切线.
(2)【解】如图,连接OF与AC交于点M.
∵OA=OC,∠BAC=30°,∴∠BAC=∠ACO=30°.∴∠BOC=60°.
∵AD⊥CE,由(1)知OC⊥CE,∴AD∥OC.∴∠FAM=∠OCM=30°,∠FAB=∠BOC=60°.
又∵OA=OF,∴△AFO为等边三角形.∴AF=OA=OC.
又∵∠FMA=∠OMC,∴△AFM≌△COM.∴∴
∵C为的中点,∴∠FOC=∠BOC=60°.
∵AB=4,∴FO=OC=OB=2.即阴影部分的面积为π.
12.π-1【点拨】如图,设以BC为直径的半圆与AB交于点D,连接CD.
在Rt△ACB中,AC=BC=2,
∵BC是半圆的直径,∴∠CDB=90°,即CD⊥AB.
又∵CA=CB,∴CD=BD=AD=.
易知D为的中点,
∴
点方法 计算不规则图形的面积时,常常通过割补法将不,图形的面积转化为几个规则图形面积的和或差.
13.【解】(1)3;(2,1);6
(2)如图,连接AC,过点A作AD⊥BC于点D,则BC=2DC.
∵⊙A的半径AC=2,由A(5,1)可得AD=1,
∴在Rt△ADC中,
14.【解】易知,三个扇形的半径都为1,三个扇形圆心角的度数和为∴阴影部分面积的和为
点方法 利用凑整法可将图中阴影部分拼成一个圆心角为135°、半径是1的扇形,
15.C【点拨】在等腰直角三角形ABC中,∠ACB=90°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
