2025--2026年湖南省邵阳市九年级数学人教版上学期第25章--26章综合能力基础练习试卷(含解析)
文档属性
| 名称 | 2025--2026年湖南省邵阳市九年级数学人教版上学期第25章--26章综合能力基础练习试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 09:55:47 | ||
图片预览




文档简介
2025--2026年湖南省邵阳市九年级数学人教版
上学期第25章--26章综合能力基础练习试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
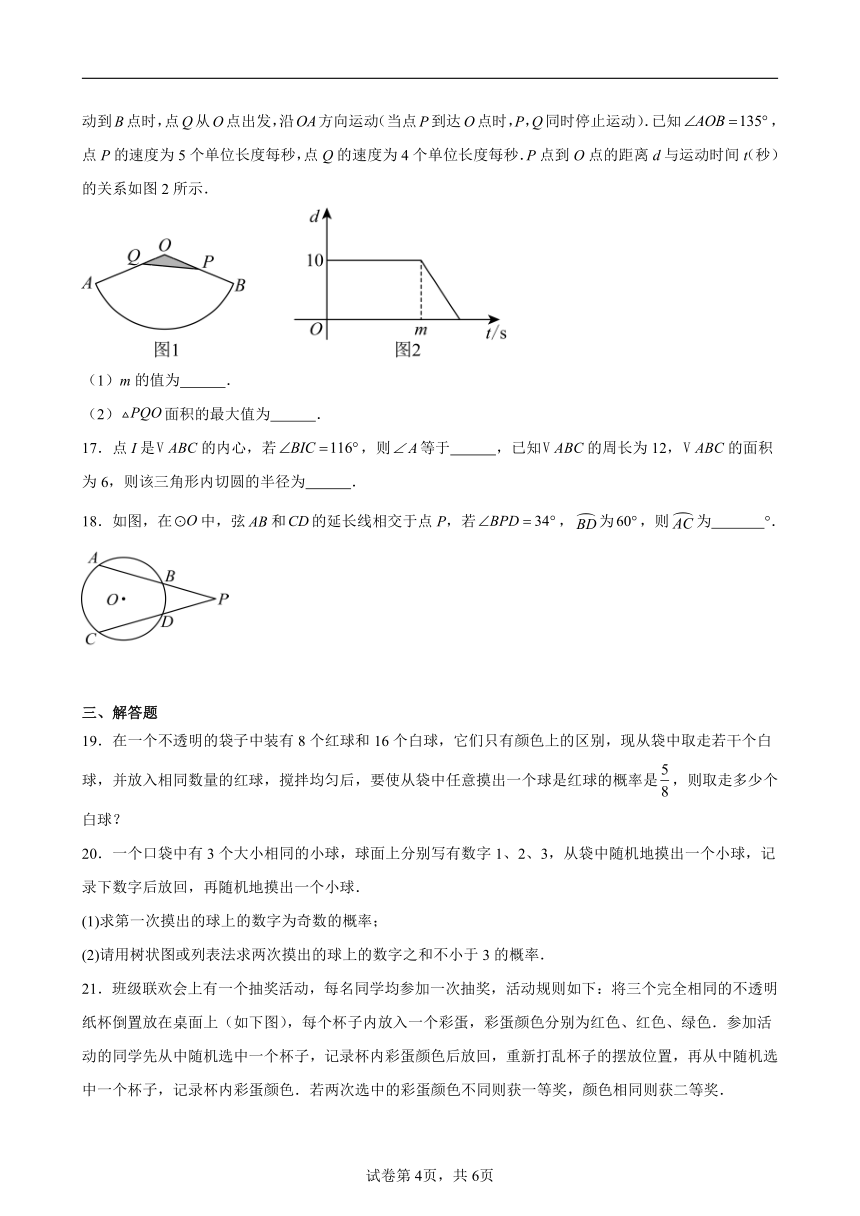
1.如图,四个转盘分别被分成不同的等份,若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是( )
A. B.
C. D.
2.将一个正六面体骰子掷一次,它的点数恰好是4的概率是( )
A. B. C. D.
3.下列事件是随机事件的是( )
A.通常加热到时,水沸腾
B.任意画一个四边形,其内角和是
C.射击运动员射击一次,命中靶心
D.明天太阳从东方升起
4.已知的半径为,,则点P与的位置关系是( )
A.点P在内 B.点P在上
C.点P在外 D.无法确定
5.如图,点A、B、C、D在上,,,则( )
A. B. C. D.
6.如图,内接于,,,为的直径,,那么的值为( )
A.4 B. C. D.2
7.下列说话正确的是( )
A.检测某城市的空气质量,用全面调查 B.了解全国中学生的视力和用眼卫生情况,用抽样调查
C.篮球队员在罚球线上投篮一次,未投中是必然事件 D.任意画一个三角形,其内角和是是随机事件
8.下列事件是不可能事件的是( )
A.射击运动员射击一次,命中靶心
B.投一枚图钉,钉尖朝上
C.把一粒种子种在花盆中,种子发芽
D.水中捞月
9.如图,在等腰中,,点O是边中点,的半径为1,点P是边上一动点,则由点P到的切线长的最小值为( )
A. B. C. D.
10.如图,四边形内接于,,,的直径为,四边形的周长为,的长为,则关于的函数关系式是( )
A. B.
C. D.
二、填空题
11.一个密码锁的密码由三个数字组成,每个数字都是0至9这十个数字中的一个,只有当三个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了中间的数字,他一次就能打开该锁的概率是 .
12.一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是 ;
13.如图,在 中,弦 等于 的半径, 交 于点 ,则 .
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,为半径的圆,且圆心在水面上方,若圆被水面截得的弦长为,当筒车工作时,则盛水桶在水面以下的最大深度为 m.
15.如图,是的直径,弦与交于点,若,,则的半径为 .
16.如图1,在扇形中,点P从A点出发,沿运动至B点,再沿线段运动至O点.当点P运动到B点时,点Q从O点出发,沿方向运动(当点P到达O点时,P,Q同时停止运动).已知,点P的速度为5个单位长度每秒,点Q的速度为4个单位长度每秒.P点到O点的距离d与运动时间t(秒)的关系如图2所示.
(1)m的值为 .
(2)面积的最大值为 .
17.点I是的内心,若,则等于 ,已知的周长为12,的面积为6,则该三角形内切圆的半径为 .
18.如图,在中,弦和的延长线相交于点P,若,为,则为 °.
三、解答题
19.在一个不透明的袋子中装有8个红球和16个白球,它们只有颜色上的区别,现从袋中取走若干个白球,并放入相同数量的红球,搅拌均匀后,要使从袋中任意摸出一个球是红球的概率是,则取走多少个白球?
20.一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)求第一次摸出的球上的数字为奇数的概率;
(2)请用树状图或列表法求两次摸出的球上的数字之和不小于3的概率.
21.班级联欢会上有一个抽奖活动,每名同学均参加一次抽奖,活动规则如下:将三个完全相同的不透明纸杯倒置放在桌面上(如下图),每个杯子内放入一个彩蛋,彩蛋颜色分别为红色、红色、绿色.参加活动的同学先从中随机选中一个杯子,记录杯内彩蛋颜色后放回,重新打乱杯子的摆放位置,再从中随机选中一个杯子,记录杯内彩蛋颜色.若两次选中的彩蛋颜色不同则获一等奖,颜色相同则获二等奖.
(1)“随机选中一个杯子,杯内彩蛋颜色是黑色”是 事件(填“随机”“必然”或“不可能”);
(2)请用画树状图(或列表)的方法,求某同学获一等奖的概率.
22.在某次数学活动中,有两个如图所示的转盘,转盘A被分成四个相同的扇形,分别标有数字1、2、3、4,转盘B被分成三个相同的扇形,分别标有数字5、6、7,指针固定不变,转动转盘(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止).小滨自由转动A盘,小河自由转动B盘,当两个转盘停止后,记下各个转盘指针所指区域内对应的数字,请用画树状图或列表法求所得两数之和为的倍数的概率.
23.如图,,,均为的直径,点是弧的中点,点在上,且四边形是平行四边形,.
(1)求证:;
(2)若点在的延长线上,且,证明:是的切线;
(3)求的半径.
24.如图,在中,是直径,弦,垂足为点E,连结,.
(1)求证:.
(2)若,,求的长度.
25.用一个圆心角为,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面半径是多少?
26.如图,在平面直角坐标系中,点,,
(1)以点C为旋转中心,把逆时针旋转,画出旋转后的;
(2)在(1)的条件下,求点B经过的路径长.
试卷第1页,共3页
试卷第1页,共3页
《2025--2026年湖南省邵阳市九年级数学人教版 上学期第25章--26章综合能力基础练习试卷》参考答案
1.D
【分析】此题主要考查了几何概率,计算阴影区域的面积在总面积中占的比例是解题关键.利用指针落在阴影区域内的概率阴影部分面积总面积,分别求出概率比较即可.
【详解】解:A、指针落在阴影区域内的概率为;
B、指针落在阴影区域内的概率是;
C、指针落在阴影区域内的概率为;
D、指针落在阴影区域内的概率为,
,
指针落在阴影区域内的概率最大的转盘是D选项.
故选:D.
2.A
【分析】列举出所有情况,看所求的情况占总情况的多少即可.
【详解】解:骰子上有6个数,点数是4的只有6种情况,
∴点数是4的概率是.
故选:A.
【点睛】考查了列表法和树状图法,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率.注意本题是放回实验.
3.C
【分析】本题考查事件的分类,根据生活常识及四边形内角和即可判断答案,解决本题需要熟记事件分为必然事件、不可能事件、随机事件,必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.熟记事件分类及相关定义是解决问题的关键.
【详解】解:A、通常加热到时,水沸腾,是必然事件,不符合题意;
B、由四边形内角和为,则任意画一个四边形,其内角和是,是不可能事件,不符合题意;
C、射击运动员射击一次,命中靶心,是随机事件,符合题意;
D、明天太阳从东方升起,是必然事件,不符合题意;
故选:C.
4.A
【分析】本题考查的是点与圆的位置关系:当点到圆心距离小于半径时,点在圆内;当点到圆心距离等于半径时,点在圆上;当点到圆心距离大于半径时,点在圆外. 根据点到圆心的距离即可得出答案.
【详解】解:∵
即的半径,
∴点P在内,
故选:A.
5.D
【分析】本题考查了圆周角定理,平行线的性质,三角形的内角和定理,等腰三角形的性质,正确添加辅助线是解题的关键.连接,则,由平行线的性质以及等腰三角形得到,再由三角形内角和定理求出,再由角度和差计算即可.
【详解】解:连接,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
故选:D.
6.A
【分析】本题考查了等边对等角、三角形内角和定理、圆周角定理、含角的直角三角形的性质,根据等边对等角结合三角形内角和定理得出,由圆周角定理得出,,再由含角的直角三角形的性质即可得出答案.
【详解】解:,,
∴,
∵,
,
为的直径,
,
在中,,
∴,
故选:A.
7.B
【分析】本题主要考查了事件的分类,全面调查,抽样调查等知识.根据事件的分类,全面调查,抽样调查对各选项进行判断作答即可,熟练掌事件的分类,全面调查,抽样调查是解题的关键.
【详解】A、检测某城市的空气质量,用抽样调查,原说法错误,不符合题意;
B、了解全国中学生的视力和用眼卫生情况,用抽样调查,原说法正确,故符合题意;
C、“篮球队员在罚球线上投篮一次,未投中”是随机事件,原说法错误,不符合题意;
D、“任意画一个三角形,其内角和是是不可能事件”,原说法错误,不符合题意;
故选:B.
8.D
【分析】本题考查了随机事件,掌握事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,可以有发生也可能不发生的事件叫随机事件是解题的关键.
根据不可能事件的定义判断即可.
【详解】解:A、“射击运动员射击一次,命中靶心”是随机事件,不符合题意;
B、“投一枚图钉,钉尖朝上”是随机事件,不符合题意;
C、“把一粒种子种在花盆中,种子发芽”是随机事件,不符合题意;
D、“水中捞月”是不可能事件,符合题意;
故选:D.
9.B
【分析】本题考查动态几何和勾股定理,转化线段的最小值,找到位置是解题的关键.先确定最小值时的位置为最短时,线段最小,再利用勾股定理解题.
【详解】解:如图,连接,
与相切于点Q,
,
当最短时,线段最小,
当时,线段最小,
点O是边的中点,
,
,
,
,
,即P到的切线长的最小值为.
故选:B.
10.B
【分析】过点作交的延长线于,连接,先证明是等腰直角三角形,为直径,则,而得,证明是等腰直角三角形得,,然后证明和全等得,则,即可得出答案.
【详解】解:过点作交的延长线于,连接,如图所示:
四边形内接于,,,
为的直径,是等腰直角三角形,
,,
,,
,
是等腰直角三角形,
,,
∴,
,,
,
,,
,,
,
在和中,
,
,
,
,
故选:B.
【点睛】本题考查了圆内接四边形的性质,等腰直角三角形的判定和性质,圆周角定理,全等三角形的判定和性质,勾股定理,理解圆内接四边形的性质,等腰直角三角形的判定和性质,圆周角定理,熟练掌握全等三角形的判定和性质,灵活运用勾股定理进行计算是解决问题的关键.
11.
【分析】根据中间一个数字共有0至9十种情况,其中只有一种能打开,利用概率公式进行求解即可.
【详解】因为密码由三个数字组成,个位和百位上的数字已经确定,中间一个数字为0至9这十个数字中的一个,所以一次就能打开该锁的概率是.
故答案为:
【点睛】本题考查了简单概率公式的计算,熟悉概率公式是解题的关键,如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件A的概率.
12.
【分析】根据概率公式直接进行计算即可得解.
【详解】解:从袋子中随机摸出一个小球,共有9种等可能的结果,其中摸出的小球是红球的结果有6种,
∴摸出的小球是红球的概率是;
故答案为:.
【点睛】本题考查概率.熟练掌握概率公式,是解题的关键.
13./30度
【分析】根据题意可得是等边三角形,再结合,得到.
【详解】解:∵弦 等于 的半径,
∴是等边三角形,
∴,
∵,
∴,
故答案为:.
【点睛】本题考查了等边三角形的性质和圆的性质,灵活运用所学知识是解题关键.
14.1
【分析】本题主要考查垂径定理,熟练掌握垂径定理是解题的关键;过点O作,交于点C,交于点H,则有,然后根据勾股定理可进行求解.
【详解】解:过点O作,交于点C,交于点H,如图所示:
∴,
∴,
∴;
故答案为:1.
15.2
【分析】此题考查垂径定理,勾股定理,等腰直角三角形的性质与判定等,把式子进行变形是解题的关键.过点作, 连接,根据垂径定理可得根据得到对式子进行变换,即可求出半径.
【详解】解:设的半径为R,过点作, 连接,
,
∴是等腰直角三角形,
,
∴
,
在中,由勾股定理得,
∴,
解得或(舍去),
∴的半径为2.
故答案为:2.
16.
【分析】本题考查了动点问题的函数图象,列函数解析式是解题的关键.
(1)由图象得扇形的半径为10,根据弧长公式求出的长即可求解;
(2)根据二次函数的性质求解.
【详解】解:(1)由图象得:扇形的半径为10,
∴ ,
∴,
故答案为:;
(2)设从点B处开始经过时,面积的面积为y,
则:
∴
∵,
∵,
∴当时,y随x的增大而增大,
∴当时,y取最大值,为,
故答案为:.
17. /52度 1
【分析】本题方要考查了三角形角平分线的性质、内切圆与内心性质、三角形面积公式等知识点,熟悉角平分线相关性质与结论是解答本题的关键.根据三角形两条内角平分线相交所形成的角,即可计算出,进而得到,由三角形内角和定理即可求出;根据三角形的面积等于周长与内切圆半径乘积的一半,据此算出答案.
【详解】解:如图,
∵点I是的内心,,
∴,
∴,
∴.
设内切圆半径为r,则,
故答案为:,1.
18.
【分析】本题主要考查圆周角定理,三角形外角和定理,熟练掌握圆周角定理是解题的关键.连接,根据圆周角定理求出的度数,由三角形外角的性质求出的度数,最后再根据圆周角定理求出的度数即可.
【详解】解:如图,连接.
,
,
,
.
故答案为:.
19.取走7个白球
【分析】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.取走x个白球,则放入x个红球,根据题意可得=,解方程即可求得答案.
【详解】解:设取走x个白球,则放入x个红球,
根据题意可得,
解得,
所以取走7个白球.
20.(1)
(2)
【分析】直接根据概率公式用出现情况数除以总情况数即可.
画树状图即可.
【详解】(1)∵奇数出现的情况是2种,总情况有3种,
∴概率为:.
(2)画树状图为:
则共有9种等可能结果,
∴两次摸出的球上的数字之和不小于3的情况有8种,
∴概率为:.
【点睛】本题考查了概率的求法及树状图的画法,掌握概率=所求情况与总情况之比.
21.(1)不可能
(2)
【分析】(1)根据事件的分类标准判断解答即可.
(2)利用画树状图法解答即可.
本题考查了事件,树状图法求概率,熟练掌握画树状图法求概率是解题的关键.
【详解】(1)解:根据题意,得杯内彩蛋颜色是黑色”是不可能事件,
故答案为:不可能.
(2)解:根据题意,画树状图如下:
由图可知,共有9种等可能的结果,其中两次选中的彩蛋颜色不同的有4种,
∴获一等奖的概率.
22.所得两数之和为3的倍数的概率为
【分析】本题考查列表法与树状图法,画出树状图,然后根据概率公式列式计算即可得解;解题的关键是掌握:概率等于所求情况数与总情况数之比.
【详解】解:根据题意画出树状图如下:
一共有12种情况,两数之和为3的倍数的情况有4种,
∴P(两数之和为3的倍数),
答:所得两数之和为3的倍数的概率为.
23.(1)见解析
(2)见解析
(3)
【分析】(1)证明,又由,,即可证明;
(2)连接交于点.由得到,由圆周角定理得到,已知,得到,则.由点是弧的中点得到半径,则半径,即可证明是的切线;
(3)设的半径为.证明,..求出,则.由得到.根据勾股定理得到,则,解方程即可求出的半径.
【详解】(1)证明:∵点是弧的中点,
∴
∴.
∵,,
∴.
∵,,
∴.
(2)证明:连接交于点.
∵,
∴,且,
∵,
∴,
∴.
∵点是弧的中点,
∴半径,
∴半径,
∴是的切线.
(3)解:设的半径为.
∵四边形是平行四边形,
∴,.
∵,
∴.
∵点是的中点,
∴点是的中点.
∵点是的中点,
∴,
∴.
∵,
∴.
∵,
∴,
整理得,
解得或(舍去).
∴的半径为.
【点睛】此题考查了圆周角定理、切线的判定、垂径定理、勾股定理、平行四边形的性质、全等三角形的判定和性质等知识,综合性较强,熟练掌握圆的相关性质是解题的关键.
24.(1)证明见解析
(2)
【分析】本题考查了垂径定理,圆周角定理,弧长公式,正确掌握相关性质内容是解题的关键.
(1)因为是直径,所以,结合圆周角定理,即可作答.
(2)因为是直径,所以,即,故,则,再运用弧长公式列式计算,即可作答.
【详解】(1)证明:,是直径,
,
;
(2)解:如图,连接,,.
,是直径,
,
,
,
,
,
的长.
25.
【分析】本题考查了圆锥的底面周长,弧长公式,利用底面周长展开图的弧长可得.解答本题的关键是有确定底面周长展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.
【详解】解:扇形的弧长,
设圆锥底面半径为,
故可得,
解得.
底面圆的半径为.
26.(1)见解析;
(2).
【分析】本题考查了作图-旋转变换,弧长公式,勾股定理等知识,掌握相关知识是解题的关键.
(1)利用旋转变换的性质分别作出的对应点,依次连接即可;
(2)由勾股定理求出,再利用弧长公式即可求解.
【详解】(1)解:作出点、以点C为旋转中心,把逆时针旋转的对应点、,依次连接 、、,则即为所求,如图所示:
(2)解:由网格和勾股定理可得:,
由题意可得:,
点B经过的路径长为.
答案第1页,共2页
上学期第25章--26章综合能力基础练习试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四个转盘分别被分成不同的等份,若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是( )
A. B.
C. D.
2.将一个正六面体骰子掷一次,它的点数恰好是4的概率是( )
A. B. C. D.
3.下列事件是随机事件的是( )
A.通常加热到时,水沸腾
B.任意画一个四边形,其内角和是
C.射击运动员射击一次,命中靶心
D.明天太阳从东方升起
4.已知的半径为,,则点P与的位置关系是( )
A.点P在内 B.点P在上
C.点P在外 D.无法确定
5.如图,点A、B、C、D在上,,,则( )
A. B. C. D.
6.如图,内接于,,,为的直径,,那么的值为( )
A.4 B. C. D.2
7.下列说话正确的是( )
A.检测某城市的空气质量,用全面调查 B.了解全国中学生的视力和用眼卫生情况,用抽样调查
C.篮球队员在罚球线上投篮一次,未投中是必然事件 D.任意画一个三角形,其内角和是是随机事件
8.下列事件是不可能事件的是( )
A.射击运动员射击一次,命中靶心
B.投一枚图钉,钉尖朝上
C.把一粒种子种在花盆中,种子发芽
D.水中捞月
9.如图,在等腰中,,点O是边中点,的半径为1,点P是边上一动点,则由点P到的切线长的最小值为( )
A. B. C. D.
10.如图,四边形内接于,,,的直径为,四边形的周长为,的长为,则关于的函数关系式是( )
A. B.
C. D.
二、填空题
11.一个密码锁的密码由三个数字组成,每个数字都是0至9这十个数字中的一个,只有当三个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了中间的数字,他一次就能打开该锁的概率是 .
12.一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是 ;
13.如图,在 中,弦 等于 的半径, 交 于点 ,则 .
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,为半径的圆,且圆心在水面上方,若圆被水面截得的弦长为,当筒车工作时,则盛水桶在水面以下的最大深度为 m.
15.如图,是的直径,弦与交于点,若,,则的半径为 .
16.如图1,在扇形中,点P从A点出发,沿运动至B点,再沿线段运动至O点.当点P运动到B点时,点Q从O点出发,沿方向运动(当点P到达O点时,P,Q同时停止运动).已知,点P的速度为5个单位长度每秒,点Q的速度为4个单位长度每秒.P点到O点的距离d与运动时间t(秒)的关系如图2所示.
(1)m的值为 .
(2)面积的最大值为 .
17.点I是的内心,若,则等于 ,已知的周长为12,的面积为6,则该三角形内切圆的半径为 .
18.如图,在中,弦和的延长线相交于点P,若,为,则为 °.
三、解答题
19.在一个不透明的袋子中装有8个红球和16个白球,它们只有颜色上的区别,现从袋中取走若干个白球,并放入相同数量的红球,搅拌均匀后,要使从袋中任意摸出一个球是红球的概率是,则取走多少个白球?
20.一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)求第一次摸出的球上的数字为奇数的概率;
(2)请用树状图或列表法求两次摸出的球上的数字之和不小于3的概率.
21.班级联欢会上有一个抽奖活动,每名同学均参加一次抽奖,活动规则如下:将三个完全相同的不透明纸杯倒置放在桌面上(如下图),每个杯子内放入一个彩蛋,彩蛋颜色分别为红色、红色、绿色.参加活动的同学先从中随机选中一个杯子,记录杯内彩蛋颜色后放回,重新打乱杯子的摆放位置,再从中随机选中一个杯子,记录杯内彩蛋颜色.若两次选中的彩蛋颜色不同则获一等奖,颜色相同则获二等奖.
(1)“随机选中一个杯子,杯内彩蛋颜色是黑色”是 事件(填“随机”“必然”或“不可能”);
(2)请用画树状图(或列表)的方法,求某同学获一等奖的概率.
22.在某次数学活动中,有两个如图所示的转盘,转盘A被分成四个相同的扇形,分别标有数字1、2、3、4,转盘B被分成三个相同的扇形,分别标有数字5、6、7,指针固定不变,转动转盘(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止).小滨自由转动A盘,小河自由转动B盘,当两个转盘停止后,记下各个转盘指针所指区域内对应的数字,请用画树状图或列表法求所得两数之和为的倍数的概率.
23.如图,,,均为的直径,点是弧的中点,点在上,且四边形是平行四边形,.
(1)求证:;
(2)若点在的延长线上,且,证明:是的切线;
(3)求的半径.
24.如图,在中,是直径,弦,垂足为点E,连结,.
(1)求证:.
(2)若,,求的长度.
25.用一个圆心角为,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面半径是多少?
26.如图,在平面直角坐标系中,点,,
(1)以点C为旋转中心,把逆时针旋转,画出旋转后的;
(2)在(1)的条件下,求点B经过的路径长.
试卷第1页,共3页
试卷第1页,共3页
《2025--2026年湖南省邵阳市九年级数学人教版 上学期第25章--26章综合能力基础练习试卷》参考答案
1.D
【分析】此题主要考查了几何概率,计算阴影区域的面积在总面积中占的比例是解题关键.利用指针落在阴影区域内的概率阴影部分面积总面积,分别求出概率比较即可.
【详解】解:A、指针落在阴影区域内的概率为;
B、指针落在阴影区域内的概率是;
C、指针落在阴影区域内的概率为;
D、指针落在阴影区域内的概率为,
,
指针落在阴影区域内的概率最大的转盘是D选项.
故选:D.
2.A
【分析】列举出所有情况,看所求的情况占总情况的多少即可.
【详解】解:骰子上有6个数,点数是4的只有6种情况,
∴点数是4的概率是.
故选:A.
【点睛】考查了列表法和树状图法,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率.注意本题是放回实验.
3.C
【分析】本题考查事件的分类,根据生活常识及四边形内角和即可判断答案,解决本题需要熟记事件分为必然事件、不可能事件、随机事件,必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.熟记事件分类及相关定义是解决问题的关键.
【详解】解:A、通常加热到时,水沸腾,是必然事件,不符合题意;
B、由四边形内角和为,则任意画一个四边形,其内角和是,是不可能事件,不符合题意;
C、射击运动员射击一次,命中靶心,是随机事件,符合题意;
D、明天太阳从东方升起,是必然事件,不符合题意;
故选:C.
4.A
【分析】本题考查的是点与圆的位置关系:当点到圆心距离小于半径时,点在圆内;当点到圆心距离等于半径时,点在圆上;当点到圆心距离大于半径时,点在圆外. 根据点到圆心的距离即可得出答案.
【详解】解:∵
即的半径,
∴点P在内,
故选:A.
5.D
【分析】本题考查了圆周角定理,平行线的性质,三角形的内角和定理,等腰三角形的性质,正确添加辅助线是解题的关键.连接,则,由平行线的性质以及等腰三角形得到,再由三角形内角和定理求出,再由角度和差计算即可.
【详解】解:连接,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
故选:D.
6.A
【分析】本题考查了等边对等角、三角形内角和定理、圆周角定理、含角的直角三角形的性质,根据等边对等角结合三角形内角和定理得出,由圆周角定理得出,,再由含角的直角三角形的性质即可得出答案.
【详解】解:,,
∴,
∵,
,
为的直径,
,
在中,,
∴,
故选:A.
7.B
【分析】本题主要考查了事件的分类,全面调查,抽样调查等知识.根据事件的分类,全面调查,抽样调查对各选项进行判断作答即可,熟练掌事件的分类,全面调查,抽样调查是解题的关键.
【详解】A、检测某城市的空气质量,用抽样调查,原说法错误,不符合题意;
B、了解全国中学生的视力和用眼卫生情况,用抽样调查,原说法正确,故符合题意;
C、“篮球队员在罚球线上投篮一次,未投中”是随机事件,原说法错误,不符合题意;
D、“任意画一个三角形,其内角和是是不可能事件”,原说法错误,不符合题意;
故选:B.
8.D
【分析】本题考查了随机事件,掌握事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,可以有发生也可能不发生的事件叫随机事件是解题的关键.
根据不可能事件的定义判断即可.
【详解】解:A、“射击运动员射击一次,命中靶心”是随机事件,不符合题意;
B、“投一枚图钉,钉尖朝上”是随机事件,不符合题意;
C、“把一粒种子种在花盆中,种子发芽”是随机事件,不符合题意;
D、“水中捞月”是不可能事件,符合题意;
故选:D.
9.B
【分析】本题考查动态几何和勾股定理,转化线段的最小值,找到位置是解题的关键.先确定最小值时的位置为最短时,线段最小,再利用勾股定理解题.
【详解】解:如图,连接,
与相切于点Q,
,
当最短时,线段最小,
当时,线段最小,
点O是边的中点,
,
,
,
,
,即P到的切线长的最小值为.
故选:B.
10.B
【分析】过点作交的延长线于,连接,先证明是等腰直角三角形,为直径,则,而得,证明是等腰直角三角形得,,然后证明和全等得,则,即可得出答案.
【详解】解:过点作交的延长线于,连接,如图所示:
四边形内接于,,,
为的直径,是等腰直角三角形,
,,
,,
,
是等腰直角三角形,
,,
∴,
,,
,
,,
,,
,
在和中,
,
,
,
,
故选:B.
【点睛】本题考查了圆内接四边形的性质,等腰直角三角形的判定和性质,圆周角定理,全等三角形的判定和性质,勾股定理,理解圆内接四边形的性质,等腰直角三角形的判定和性质,圆周角定理,熟练掌握全等三角形的判定和性质,灵活运用勾股定理进行计算是解决问题的关键.
11.
【分析】根据中间一个数字共有0至9十种情况,其中只有一种能打开,利用概率公式进行求解即可.
【详解】因为密码由三个数字组成,个位和百位上的数字已经确定,中间一个数字为0至9这十个数字中的一个,所以一次就能打开该锁的概率是.
故答案为:
【点睛】本题考查了简单概率公式的计算,熟悉概率公式是解题的关键,如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件A的概率.
12.
【分析】根据概率公式直接进行计算即可得解.
【详解】解:从袋子中随机摸出一个小球,共有9种等可能的结果,其中摸出的小球是红球的结果有6种,
∴摸出的小球是红球的概率是;
故答案为:.
【点睛】本题考查概率.熟练掌握概率公式,是解题的关键.
13./30度
【分析】根据题意可得是等边三角形,再结合,得到.
【详解】解:∵弦 等于 的半径,
∴是等边三角形,
∴,
∵,
∴,
故答案为:.
【点睛】本题考查了等边三角形的性质和圆的性质,灵活运用所学知识是解题关键.
14.1
【分析】本题主要考查垂径定理,熟练掌握垂径定理是解题的关键;过点O作,交于点C,交于点H,则有,然后根据勾股定理可进行求解.
【详解】解:过点O作,交于点C,交于点H,如图所示:
∴,
∴,
∴;
故答案为:1.
15.2
【分析】此题考查垂径定理,勾股定理,等腰直角三角形的性质与判定等,把式子进行变形是解题的关键.过点作, 连接,根据垂径定理可得根据得到对式子进行变换,即可求出半径.
【详解】解:设的半径为R,过点作, 连接,
,
∴是等腰直角三角形,
,
∴
,
在中,由勾股定理得,
∴,
解得或(舍去),
∴的半径为2.
故答案为:2.
16.
【分析】本题考查了动点问题的函数图象,列函数解析式是解题的关键.
(1)由图象得扇形的半径为10,根据弧长公式求出的长即可求解;
(2)根据二次函数的性质求解.
【详解】解:(1)由图象得:扇形的半径为10,
∴ ,
∴,
故答案为:;
(2)设从点B处开始经过时,面积的面积为y,
则:
∴
∵,
∵,
∴当时,y随x的增大而增大,
∴当时,y取最大值,为,
故答案为:.
17. /52度 1
【分析】本题方要考查了三角形角平分线的性质、内切圆与内心性质、三角形面积公式等知识点,熟悉角平分线相关性质与结论是解答本题的关键.根据三角形两条内角平分线相交所形成的角,即可计算出,进而得到,由三角形内角和定理即可求出;根据三角形的面积等于周长与内切圆半径乘积的一半,据此算出答案.
【详解】解:如图,
∵点I是的内心,,
∴,
∴,
∴.
设内切圆半径为r,则,
故答案为:,1.
18.
【分析】本题主要考查圆周角定理,三角形外角和定理,熟练掌握圆周角定理是解题的关键.连接,根据圆周角定理求出的度数,由三角形外角的性质求出的度数,最后再根据圆周角定理求出的度数即可.
【详解】解:如图,连接.
,
,
,
.
故答案为:.
19.取走7个白球
【分析】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.取走x个白球,则放入x个红球,根据题意可得=,解方程即可求得答案.
【详解】解:设取走x个白球,则放入x个红球,
根据题意可得,
解得,
所以取走7个白球.
20.(1)
(2)
【分析】直接根据概率公式用出现情况数除以总情况数即可.
画树状图即可.
【详解】(1)∵奇数出现的情况是2种,总情况有3种,
∴概率为:.
(2)画树状图为:
则共有9种等可能结果,
∴两次摸出的球上的数字之和不小于3的情况有8种,
∴概率为:.
【点睛】本题考查了概率的求法及树状图的画法,掌握概率=所求情况与总情况之比.
21.(1)不可能
(2)
【分析】(1)根据事件的分类标准判断解答即可.
(2)利用画树状图法解答即可.
本题考查了事件,树状图法求概率,熟练掌握画树状图法求概率是解题的关键.
【详解】(1)解:根据题意,得杯内彩蛋颜色是黑色”是不可能事件,
故答案为:不可能.
(2)解:根据题意,画树状图如下:
由图可知,共有9种等可能的结果,其中两次选中的彩蛋颜色不同的有4种,
∴获一等奖的概率.
22.所得两数之和为3的倍数的概率为
【分析】本题考查列表法与树状图法,画出树状图,然后根据概率公式列式计算即可得解;解题的关键是掌握:概率等于所求情况数与总情况数之比.
【详解】解:根据题意画出树状图如下:
一共有12种情况,两数之和为3的倍数的情况有4种,
∴P(两数之和为3的倍数),
答:所得两数之和为3的倍数的概率为.
23.(1)见解析
(2)见解析
(3)
【分析】(1)证明,又由,,即可证明;
(2)连接交于点.由得到,由圆周角定理得到,已知,得到,则.由点是弧的中点得到半径,则半径,即可证明是的切线;
(3)设的半径为.证明,..求出,则.由得到.根据勾股定理得到,则,解方程即可求出的半径.
【详解】(1)证明:∵点是弧的中点,
∴
∴.
∵,,
∴.
∵,,
∴.
(2)证明:连接交于点.
∵,
∴,且,
∵,
∴,
∴.
∵点是弧的中点,
∴半径,
∴半径,
∴是的切线.
(3)解:设的半径为.
∵四边形是平行四边形,
∴,.
∵,
∴.
∵点是的中点,
∴点是的中点.
∵点是的中点,
∴,
∴.
∵,
∴.
∵,
∴,
整理得,
解得或(舍去).
∴的半径为.
【点睛】此题考查了圆周角定理、切线的判定、垂径定理、勾股定理、平行四边形的性质、全等三角形的判定和性质等知识,综合性较强,熟练掌握圆的相关性质是解题的关键.
24.(1)证明见解析
(2)
【分析】本题考查了垂径定理,圆周角定理,弧长公式,正确掌握相关性质内容是解题的关键.
(1)因为是直径,所以,结合圆周角定理,即可作答.
(2)因为是直径,所以,即,故,则,再运用弧长公式列式计算,即可作答.
【详解】(1)证明:,是直径,
,
;
(2)解:如图,连接,,.
,是直径,
,
,
,
,
,
的长.
25.
【分析】本题考查了圆锥的底面周长,弧长公式,利用底面周长展开图的弧长可得.解答本题的关键是有确定底面周长展开图的弧长这个等量关系,然后由扇形的弧长公式和圆的周长公式求值.
【详解】解:扇形的弧长,
设圆锥底面半径为,
故可得,
解得.
底面圆的半径为.
26.(1)见解析;
(2).
【分析】本题考查了作图-旋转变换,弧长公式,勾股定理等知识,掌握相关知识是解题的关键.
(1)利用旋转变换的性质分别作出的对应点,依次连接即可;
(2)由勾股定理求出,再利用弧长公式即可求解.
【详解】(1)解:作出点、以点C为旋转中心,把逆时针旋转的对应点、,依次连接 、、,则即为所求,如图所示:
(2)解:由网格和勾股定理可得:,
由题意可得:,
点B经过的路径长为.
答案第1页,共2页
同课章节目录
