(单元培优卷)第5单元 平行四边形和梯形 单元全真模拟培优卷(含解析)-2025-2026学年四年级上册数学(人教版)
文档属性
| 名称 | (单元培优卷)第5单元 平行四边形和梯形 单元全真模拟培优卷(含解析)-2025-2026学年四年级上册数学(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 141.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-03 00:00:00 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年四年级上册数学单元全真模拟培优卷(人教版)
第5单元 平行四边形和梯形
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题)
1.从平行四边形的一条边上的一点到对边可以引( )垂线.
A.一条 B.两条 C.无数条
2.如果在纸上画甲乙两条直线都与第三条直线相交成直角,那么甲乙两条直线就( )
A.互相平行 B.相交 C.互相垂直
3.当一个四边形只有一组对边平行时,它是( )
A.正方形 B.长方形 C.平行四边形 D.梯形
4.在同一平面内,两条互相平行的直线,若其中一条直线与直线a互相垂直,则另一条直线与直线a( )
A.互相平行 B.互相垂直 C.相交但不垂直 D.无法判断
5.在同一平面内,与一条直线的距离为2厘米的点有( )个。
A.1 B.2 C.0 D.无数
6.下面说法正确的是( )
A.平行线就是不相交的两条直线
B.两条直线相交,交点就是垂足
C.垂直是两条直线相交时的一种特殊位置关系
D.在纸上能画出一条完整的直线
7.电动伸缩门就是利用了平行四边形的( )的特性.
A.稳定性 B.容易变形 C.对边相等 D.对边平行
8.长方形中有( )组对边分别平行.
A.1 B.2 C.4
9.两条平行线之间( )最短.
A.直线 B.线段 C.垂线段
10.过直线外一点可以画( )条直线与这条直线平行.
A.1 B.2 C.3 D.无数条
二.填空题(共12小题)
11.数一数:图中有 个平行四边形, 个梯形.
12.从平行四边形一条边上的任意一点到对边引一条 ,这点和垂足之间的距离叫做平行四边形的 .
13.在同一平面内与一条已知直线平行的直线有 条.
14.把符合要求的图形序号填在横线上.
①两组对边分别平行,有四个直角.
②只有一组对边平行的四边形.
③两组对边形分别平行,没有直角
A.正方形 B.长方形 C.平行四边形 D.梯形.
15.过点P画出线段MN的垂线,并量出∠M的大小。∠M= °
16.经过平行四边形的一个顶点可以画 条不同的高.
17.数一数,有 条直线;
有 组平行线。
18.通过直线上一点,在同一个平面内只能画 条直线与已知直线垂直.
19.两条直线相交成 度时,这两条直线互相垂直,其中一条直线叫做另一条直线的 ,这两条直线的交点叫做 .
20.两组对边 的四边形叫做平行四边形.
21.一个长方形,它有 组互相平行的线段,有 组互相垂直的线段.
22.在一个正方形中,相邻的两条边互相 ,相对的两条边互相 .
三.判断题(共8小题)
23.从直线外一点向这条直线可以作无数条垂线。
24.平行四边形的对边平行且相等. .
25.正方形的两组对边分别平行.
26.平行四边形和梯形是两种不同的四边形。
27.平行四边形必有两个角是钝角。
28.梯形的上底和下底都和高互相垂直。
29.在同一平面内的两条直线叫做平行线. .
30.正方形中,相邻的两条边都互相垂直.
四.操作题(共3小题)
31.画出下面梯形的高.
32.如图,过已知直线外一点A,分别作已知直线的平行线和垂线。
33.按要求在方格纸上画图。(每个方格的边长为1厘米)上底是5厘米,下底是7厘米,高是6厘米的直角梯形。
五.应用题(共6小题)
34.某广场有一块平行四边形草地,草地两条相邻的边分别长15米和10米,小玲绕草地周围走了4圈,她一共走了多少米?
35.一个直角梯形的上底是8厘米,若将上底延长4厘米,则该梯形就能变成一个正方形,这个梯形的下底和高各是多少厘米?
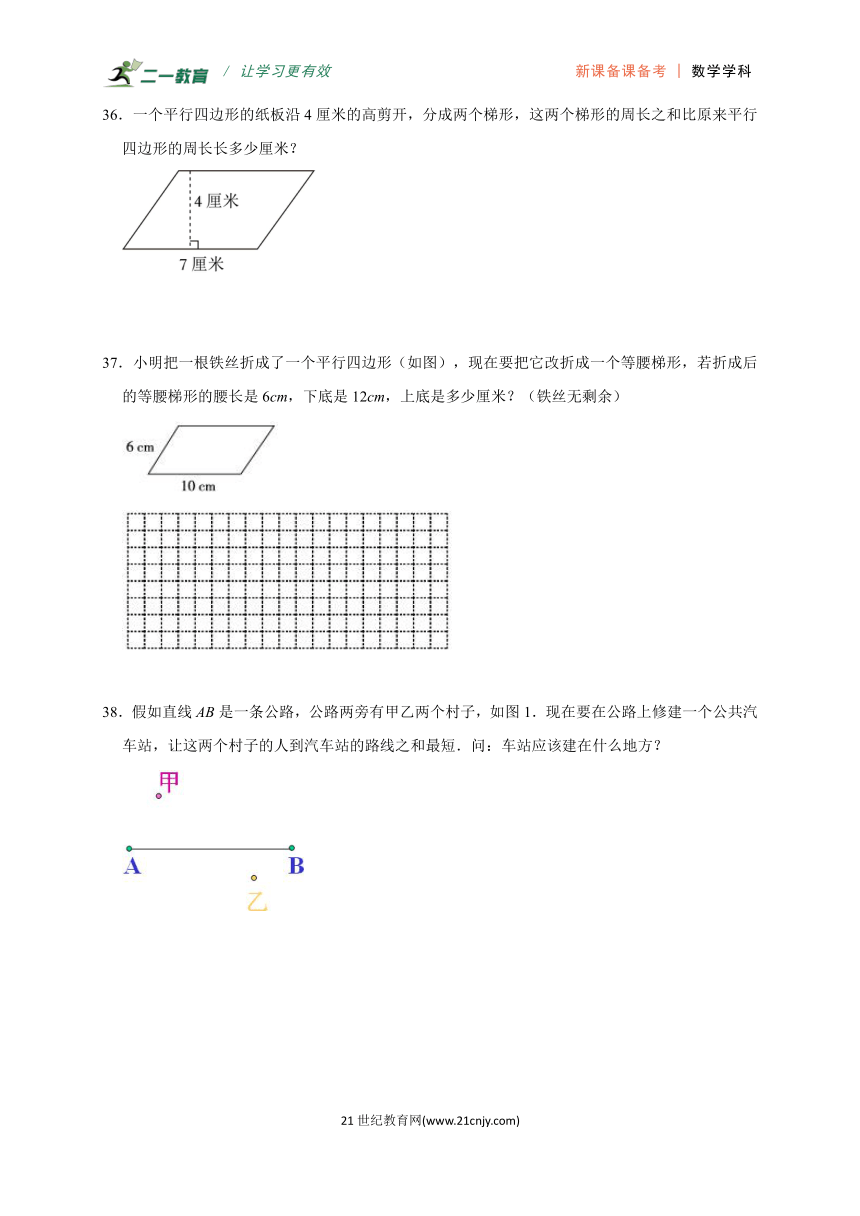
36.一个平行四边形的纸板沿4厘米的高剪开,分成两个梯形,这两个梯形的周长之和比原来平行四边形的周长长多少厘米?
37.小明把一根铁丝折成了一个平行四边形(如图),现在要把它改折成一个等腰梯形,若折成后的等腰梯形的腰长是6cm,下底是12cm,上底是多少厘米?(铁丝无剩余)
38.假如直线AB是一条公路,公路两旁有甲乙两个村子,如图1.现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短.问:车站应该建在什么地方?
39.某小区要在小区的三面围上铁栅栏(如图)。已知铁栅栏每米的成本是60元,围这三面铁栅栏需要多少钱?
参考答案及试题解析
一.选择题(共10小题)
1.A
【思路分析】因为从一条边上的一点向对边作垂线,即过直线外一点只能作一条已知直线的垂线.
【解答】解:由分析得出:从平行四边形的一条边上的一点到对边可以引一条垂线.
故选:A.
【名师点评】此题主要考查过直线外一点只能作一条已知直线的垂线.
2.A
【思路分析】因为在同一平面内,垂直于同一条直线的两条直线平行;进而得出结论.
【解答】解:根据垂直和平行的性质可知:如果在纸上画甲乙两条直线都与第三条直线相交成直角,
那么甲乙两条直线就互相平行;
故选:A。
【名师点评】此题应根据平行和垂直的特征及性质进行解答.
3.D
【思路分析】根据平行四边形和图形的定义:两组对边分别平行的四边形叫平行四边形,正方形和长方形都是特殊的平行四边形;只有一组对边平行的四边形叫梯形,即可解答.
【解答】解:当一个四边形只有一组对边平行时,它是梯形;
故选:D.
【名师点评】此题考查了平行四边形和梯形的定义.
4.B
【思路分析】根据平行线的性质:在同一个平面内,一条直线垂直于两条平行线中的一条,这条直线也必须垂直于另一条平行线。
【解答】解:在同一平面内,两条互相平行的直线,若其中一条直线与直线a互相垂直,则另一条直线与直线a互相垂直。
故选:B。
【名师点评】本题考查了平行线的性质的应用。
5.D
【思路分析】根据在同一平面内与一条直线相距2厘米的直线有上、下两条,每条直线上有无数个点,所以在同一平面内,与一条直线的距离为2厘米的点有无数个。
【解答】解:如图所示
如图可知:同一平面内与一条直线相距2厘米的直线只有2条,每条直线上有无数个点,所以在同一平面内,与一条直线的距离为2厘米的点有无数个。
故选:D。
【名师点评】此题考查了垂直和平行的特征,结合题意,作出图,是解答此题的关键。
6.C
【思路分析】平行线是指在同一平面内,不相交的两条直线,故A错误;
两条直线相交所成的角是直角,两条直线相交,交点就是垂足,相交不是直角的不是垂足,故B错误;
在同一平面内,两条直线只有相交和平行两种位置关系,垂直是一种特殊的相交,故C正确;
直线是无限长的,在一张纸上不能画出一条完整的直线,故D错误。
【解答】解:由分析可得,选项A、B、D是错误的,只有选项C正确。
故选:C。
【名师点评】此题主要考查在同一平面内,两条直线的位置关系。
7.B
【思路分析】由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,伸缩门运用了平行四边形易变形的特性.
【解答】解:伸缩门做成平行四边形的形状,是利用平行四边形的易变形的特性.
故选:B.
【名师点评】此题主要考查了平行四边形的特性是容易变形.
8.B
【思路分析】因为长方形是特殊的平行四边形,所以具备平行四边形的特征:即对边平行且相等;据此解答.
【解答】解:根据长方形的性质可得:长方形中有两组对边分别平行;
故选:B.
【名师点评】明确长方形具备平行四边形的特征,是解答此题的关键.
9.C
【思路分析】根据“在两条平行线之间的线段中,垂直两条平行线的线段最短,这条线段的长叫做平行线之间的距离”即可进行选择.
【解答】解:据分析可知:两条平行线之间垂线段最短;
故选:C.
【名师点评】此题考查了垂直和平行的特征和性质,注意基础知识的灵活运用.
10.A
【思路分析】根据平行的性质:过直线外一点,画已知直线的平行线,只能画一条;据此解答即可.
【解答】解:根据平行的性质可知:过直线外一点可以画一条直线与已知直线平行,
故选:A.
【名师点评】此题考查了平行的性质,注意基础知识的积累和运用.
二.填空题(共12小题)
11.见试题解答内容
【思路分析】(1)长方形也是特殊的平行四边形,所以由图形可知:单个的小长方形有2个,2个长方形拼成的长方形有1个,共有平行四边形2+1=3个;
(2)由两个小三角形组成的梯形有2个,由3个小三角形组成的梯形有4个,由4个小三角形组成的梯形有2个,由5个小三角形组成的梯形有2个,由6个小三角形组成的梯形有1个,所以共有2+4+2+2+1=11个.
【解答】解:根据题干分析可得,平行四边形一共有2+1=3(个),
梯形有2+4+2+2+1=11(个),
故答案为:3,11.
【名师点评】考查了图形的计数,在图形的计数时,应注重一定的顺序计数,做到不遗漏,不重复.
12.见试题解答内容
【思路分析】根据平行四边形高的含义:在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高;据此解答即可.
【解答】解:从平行四边形一条边上的任意一点到对边引一条垂线,这点和垂足之间的距离叫做平行四边形的高
故答案为:垂线,高.
【名师点评】此题考查了平行四边形高的含义,应注意灵活运用.
13.见试题解答内容
【思路分析】根据平行线的定义,在同一平面内,不相交的两条直线叫做平行线,在同一平面内与一条直线互相平行的直线有无数条;据此解答.
【解答】解:在同一平面内与一条已知直线平行的直线有 无数条;
故答案为:无数.
【名师点评】此题考查了平行的特征及性质,应注意基础知识的积累.
14.见试题解答内容
【思路分析】根据长方形、平行四边形和梯形的含义及特征:两组对边分别平行,有四个直角的四边形是长方形;只有一组对边平行的四边形是梯形;两组对边分别平行的四边形是平行四边形;由此进行解答即可.
【解答】解:①两组对边分别平行,有四个直角,是长方形;
②只有一组对边平行的四边形是梯形;
③两组对边分别平行,没有直角的四边形是平行四边形;
故选:B,D,C.
【名师点评】明确长方形、平行四边形和梯形的含义及特征,是解答此题的关键.
15.
50。
【思路分析】把三角板一直角边与MN重合,左、右滑动三角板,当点P落在三角板的另一直角边时,沿这条直角边作直线,向已知线段MN画直线即可;量角要注意:量角器的中心和角的顶点对齐,角的一边与量角器的0刻度线重合。
【解答】解:作图如下:
量得∠M的度数是50度。
故答案为:50。
【名师点评】本题考查了学生垂线的作法和量角,培养学生的作图能力。
16.见试题解答内容
【思路分析】根据平行四边形高的含义:从平行四边形一条边上的一点到它的对边引一条垂线,这一点和垂足之间的距离,即平行四边形的高;每一个顶点所对的边有两条,所以平行四边形的一个顶点可以向对边作2条高(如图);进而解答即可.
【解答】解:如图,可以作2条高:
故答案为:2.
【名师点评】此题应根据平行四边形高的含义进行分析、解答.
17.1;3。
【思路分析】(1)直线没有端点,所以图中只有一条直线;
(2),如图所示,互相平行的有:AB∥CD,AD∥BC,EF∥BD,共三组平行线。
【解答】解:(1)因为直线没有端点,所以有 1条直线;
(2),如左图所示,AB∥CD,AD∥BC,EF∥BD,所以有3组平行线。
故答案为:1;3。
【名师点评】解决本题的关键在于知道直线的特点及平行的特点。
18.见试题解答内容
【思路分析】利用定理“在同一平面内,经过直线外一点有且只有一条直线与已知直线垂直”解答即可.
【解答】解:在一个平面内,过直线外一点只能画一条直线与已知直线垂直;
故答案为:一.
【名师点评】熟记“在同一平面内,经过直线外一点有且只有一条直线与已知直线垂直”是解答本题的关键.
19.见试题解答内容
【思路分析】根据垂直的定义:如果两条直线相交成直角,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫做垂足;据此解答即可.
【解答】解:如果两条直线相交成90度时,这两条直线叫做互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫做垂足.
故答案为:90,垂线,垂足.
【名师点评】此题考查了垂直与垂足的定义.
20.见试题解答内容
【思路分析】根据平行四边形的含义:有两组对边分别平行的四边形叫做平行四边形;由此解答即可.
【解答】解:两组对边分别平行的四边形叫做平行四边形;
故答案为:分别平行.
【名师点评】本题考查了平行四边形的概念,注意基础知识的积累.
21.见试题解答内容
【思路分析】依据长方形的特征及性质可知:长方形有两组互相平行的线段,有四组互相垂直的线段,据此解答即可.
【解答】解:在一个长方形中,互相平行的线段有2组,互相垂直的有4组.
故答案为:2,4.
【名师点评】此题主要考查长方形的特征及性质.
22.见试题解答内容
【思路分析】正方形是特殊的平行四边形,根据正方形的特征:四条边都相等,四个角都是直角,可知正方形相邻的两条边互相垂直,相对的两边互相平行;据此解答.
【解答】解:正方形中相邻两条边相互垂直,相对两条边相互平行;
故选:垂直,平行.
【名师点评】此题主要考查了垂直和平行的特征及性质,用到的知识点:正方形的特征.
三.判断题(共8小题)
23.×
【思路分析】根据垂线的性质:过一点有且只有一条直线与已知直线垂直,判断即可得出答案。
【解答】解:从直线外一点,向这条直线可以作有且只有一条直线与已知直线垂直。
故答案为:×。
【名师点评】考查垂线的性质。注意理解和掌握。
24.√
【思路分析】根据平行四边形的特征:对边分别平行且长度相等;进而判断即可.
【解答】解:根据平行四边形的特征可知:平行四边形的两组对边不但平行,而且长度相等;
故答案为:√.
【名师点评】此题考查了平行四边形的特征.
25.√
【思路分析】四条边都相等的是正方形;也就是说:正方形的两组对边分别平行,它是特殊的平行四边形;由此解答即可.
【解答】解:正方形的两组对边分别平行,说法正确;
故答案为:√.
【名师点评】此题应根据正方形的特征进行解答.
26.√
【思路分析】平行四边形:两组对边分别平行的四边形;梯形:只有一组对边平行的四边形,它们是两种不同的四边形,由此判断。
【解答】解:
平行四边形和梯形是两种不同的四边形,原题说法正确。
故答案为:√。
【名师点评】此题根据平行四边形、梯形的特征进行解答即可。
27.×
【思路分析】根据平行四边形的对角相等,内角和等于360°,但应该考虑特殊的平行四边形(长方形和正方形)。
【解答】解:长方形和正方形是特殊的平行四边形,长方形和正方形的四个角都是直角,所以说”平行四边形有2个锐角和2个钝角“,说法是错误的。
故答案为:×。
【名师点评】熟练掌握平行四边形的特征,是解答此题的关键。
28.√
【思路分析】梯形两底间的距离叫做梯形的高。
【解答】解:由分析可知:梯形的高与上底和下底互相垂直,所以题干的说法是正确的。
故答案为:√。
【名师点评】本题是考查作梯形的高的意义。
29.见试题解答内容
【思路分析】根据平行线的定义:在同一平面内不相交的两条直线叫做平行线;据此解答即可.
【解答】解:因为在同一平面内不相交的两条直线叫做平行线;
所以上面的说法是错误的.
故答案为:×.
【名师点评】此题考查了平行线的定义.
30.见试题解答内容
【思路分析】正方形的特征:有4条边,4条边长度相等,4个角,都是直角;据此可知正方形的对边互相平行,相邻的两条边互相垂直.
【解答】解:正方形中,相邻的两条边都互相垂直;
故答案为:√.
【名师点评】此题考查正方形的特征,也考查了垂直的意义.
四.操作题(共3小题)
31.见试题解答内容
【思路分析】梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高.
【解答】解:画出下面梯形的高(红色虚线).
【名师点评】本题是考查作梯形的高.注意作高用虚线,并标出垂足.
32.
【思路分析】把三角板一直角边与直线重合,左、右滑动三角板,当点A落在三角板的另一直角边时,这A点沿这条直角边,向已知直线画直线即可;把三角板任一边与直线重合,另边紧靠一直尺,沿直尺滑动三角板,当与直线重合的一边结过点A时,没这边画直线,所画直线就是过A点已知直线的平行线。
【解答】解:根据题意作图如下:
【名师点评】本题考查了学生垂线的作法和平行线的作法,培养学生的作图能力。
33.
【思路分析】解:先画直角梯形的高,然后在高的两端分别取直角向同一侧画出上底和下底,最后将上底和下底末端连起来成为梯形的另一条腰。
【解答】解:画图如下:
【名师点评】此题重点考查梯形的认识及作图能力。
五.应用题(共6小题)
34.200米。
【思路分析】根据平行四边形的周长=两邻边的和×2,求出周长,再乘4即可。
【解答】解:(15+10)×2×4
=25×2×4
=200(米)
答:她一共走了200米。
【名师点评】熟练掌握平行四边形的周长公式,是解答此题的关键。
35.12厘米;12厘米。
【思路分析】由题意可知,若将上底延长4厘米,则该梯形就能变成一个正方形,那么下底就是8+4=12(厘米),高也是12厘米,据此解答即可。
【解答】解:8+4=12(厘米)
答:这个梯形的下底和高都是12厘米。
【名师点评】该梯形就能变成一个正方形,这是解答此题的关键条件。
36.见试题解答内容
【思路分析】这两个梯形的周长之和比原来平行四边形的周长多了两个4厘米,据此解答即可。
【解答】解:4+4=8(厘米)
答:这两个梯形的周长之和比原来平行四边形的周长长8厘米。
【名师点评】能找出这两个梯形的周长之和与原来平行四边形的周长的关系,是解答此题的关键。
37.8厘米。
【思路分析】先算出平行四边形的周长。再求梯形的上底长即可。
【解答】解:(10+6)×2
=16×2
=32(厘米)
32﹣6×2﹣12
=32﹣12﹣12
=8(厘米)
答:上底是8厘米。
【名师点评】熟练掌握平行四边形的对边相等的性质,是解答此题的关键。
38.见试题解答内容
【思路分析】本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来路程之和最短,因为两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(如图):
【解答】解:用直线把甲村、乙村连起来.因为甲村乙村在公路的两侧,
所以这条连线必与公路AB有一个交点,
设这个交点为P,那么在P点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短.
【名师点评】两点之间的距离,线段最短,根据此性质解决问题.
39.22200元。
【思路分析】把已知的这三条边的长度相加即能求出铁栅栏的长度,再用铁栅栏的长度乘每米铁栅栏需要的钱数即可求解。
【解答】解:(120+90+160)×60
=370×60
=22200(元)
答:围这三面铁栅栏需要22200元钱。
【名师点评】本题考查了梯形周长的意义和计算方法的应用。
21世纪教育网(www.21cnjy.com)
2025-2026学年四年级上册数学单元全真模拟培优卷(人教版)
第5单元 平行四边形和梯形
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题)
1.从平行四边形的一条边上的一点到对边可以引( )垂线.
A.一条 B.两条 C.无数条
2.如果在纸上画甲乙两条直线都与第三条直线相交成直角,那么甲乙两条直线就( )
A.互相平行 B.相交 C.互相垂直
3.当一个四边形只有一组对边平行时,它是( )
A.正方形 B.长方形 C.平行四边形 D.梯形
4.在同一平面内,两条互相平行的直线,若其中一条直线与直线a互相垂直,则另一条直线与直线a( )
A.互相平行 B.互相垂直 C.相交但不垂直 D.无法判断
5.在同一平面内,与一条直线的距离为2厘米的点有( )个。
A.1 B.2 C.0 D.无数
6.下面说法正确的是( )
A.平行线就是不相交的两条直线
B.两条直线相交,交点就是垂足
C.垂直是两条直线相交时的一种特殊位置关系
D.在纸上能画出一条完整的直线
7.电动伸缩门就是利用了平行四边形的( )的特性.
A.稳定性 B.容易变形 C.对边相等 D.对边平行
8.长方形中有( )组对边分别平行.
A.1 B.2 C.4
9.两条平行线之间( )最短.
A.直线 B.线段 C.垂线段
10.过直线外一点可以画( )条直线与这条直线平行.
A.1 B.2 C.3 D.无数条
二.填空题(共12小题)
11.数一数:图中有 个平行四边形, 个梯形.
12.从平行四边形一条边上的任意一点到对边引一条 ,这点和垂足之间的距离叫做平行四边形的 .
13.在同一平面内与一条已知直线平行的直线有 条.
14.把符合要求的图形序号填在横线上.
①两组对边分别平行,有四个直角.
②只有一组对边平行的四边形.
③两组对边形分别平行,没有直角
A.正方形 B.长方形 C.平行四边形 D.梯形.
15.过点P画出线段MN的垂线,并量出∠M的大小。∠M= °
16.经过平行四边形的一个顶点可以画 条不同的高.
17.数一数,有 条直线;
有 组平行线。
18.通过直线上一点,在同一个平面内只能画 条直线与已知直线垂直.
19.两条直线相交成 度时,这两条直线互相垂直,其中一条直线叫做另一条直线的 ,这两条直线的交点叫做 .
20.两组对边 的四边形叫做平行四边形.
21.一个长方形,它有 组互相平行的线段,有 组互相垂直的线段.
22.在一个正方形中,相邻的两条边互相 ,相对的两条边互相 .
三.判断题(共8小题)
23.从直线外一点向这条直线可以作无数条垂线。
24.平行四边形的对边平行且相等. .
25.正方形的两组对边分别平行.
26.平行四边形和梯形是两种不同的四边形。
27.平行四边形必有两个角是钝角。
28.梯形的上底和下底都和高互相垂直。
29.在同一平面内的两条直线叫做平行线. .
30.正方形中,相邻的两条边都互相垂直.
四.操作题(共3小题)
31.画出下面梯形的高.
32.如图,过已知直线外一点A,分别作已知直线的平行线和垂线。
33.按要求在方格纸上画图。(每个方格的边长为1厘米)上底是5厘米,下底是7厘米,高是6厘米的直角梯形。
五.应用题(共6小题)
34.某广场有一块平行四边形草地,草地两条相邻的边分别长15米和10米,小玲绕草地周围走了4圈,她一共走了多少米?
35.一个直角梯形的上底是8厘米,若将上底延长4厘米,则该梯形就能变成一个正方形,这个梯形的下底和高各是多少厘米?
36.一个平行四边形的纸板沿4厘米的高剪开,分成两个梯形,这两个梯形的周长之和比原来平行四边形的周长长多少厘米?
37.小明把一根铁丝折成了一个平行四边形(如图),现在要把它改折成一个等腰梯形,若折成后的等腰梯形的腰长是6cm,下底是12cm,上底是多少厘米?(铁丝无剩余)
38.假如直线AB是一条公路,公路两旁有甲乙两个村子,如图1.现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短.问:车站应该建在什么地方?
39.某小区要在小区的三面围上铁栅栏(如图)。已知铁栅栏每米的成本是60元,围这三面铁栅栏需要多少钱?
参考答案及试题解析
一.选择题(共10小题)
1.A
【思路分析】因为从一条边上的一点向对边作垂线,即过直线外一点只能作一条已知直线的垂线.
【解答】解:由分析得出:从平行四边形的一条边上的一点到对边可以引一条垂线.
故选:A.
【名师点评】此题主要考查过直线外一点只能作一条已知直线的垂线.
2.A
【思路分析】因为在同一平面内,垂直于同一条直线的两条直线平行;进而得出结论.
【解答】解:根据垂直和平行的性质可知:如果在纸上画甲乙两条直线都与第三条直线相交成直角,
那么甲乙两条直线就互相平行;
故选:A。
【名师点评】此题应根据平行和垂直的特征及性质进行解答.
3.D
【思路分析】根据平行四边形和图形的定义:两组对边分别平行的四边形叫平行四边形,正方形和长方形都是特殊的平行四边形;只有一组对边平行的四边形叫梯形,即可解答.
【解答】解:当一个四边形只有一组对边平行时,它是梯形;
故选:D.
【名师点评】此题考查了平行四边形和梯形的定义.
4.B
【思路分析】根据平行线的性质:在同一个平面内,一条直线垂直于两条平行线中的一条,这条直线也必须垂直于另一条平行线。
【解答】解:在同一平面内,两条互相平行的直线,若其中一条直线与直线a互相垂直,则另一条直线与直线a互相垂直。
故选:B。
【名师点评】本题考查了平行线的性质的应用。
5.D
【思路分析】根据在同一平面内与一条直线相距2厘米的直线有上、下两条,每条直线上有无数个点,所以在同一平面内,与一条直线的距离为2厘米的点有无数个。
【解答】解:如图所示
如图可知:同一平面内与一条直线相距2厘米的直线只有2条,每条直线上有无数个点,所以在同一平面内,与一条直线的距离为2厘米的点有无数个。
故选:D。
【名师点评】此题考查了垂直和平行的特征,结合题意,作出图,是解答此题的关键。
6.C
【思路分析】平行线是指在同一平面内,不相交的两条直线,故A错误;
两条直线相交所成的角是直角,两条直线相交,交点就是垂足,相交不是直角的不是垂足,故B错误;
在同一平面内,两条直线只有相交和平行两种位置关系,垂直是一种特殊的相交,故C正确;
直线是无限长的,在一张纸上不能画出一条完整的直线,故D错误。
【解答】解:由分析可得,选项A、B、D是错误的,只有选项C正确。
故选:C。
【名师点评】此题主要考查在同一平面内,两条直线的位置关系。
7.B
【思路分析】由平行四边形的特性可知,平行四边形具有不稳定性,所以容易变形,伸缩门运用了平行四边形易变形的特性.
【解答】解:伸缩门做成平行四边形的形状,是利用平行四边形的易变形的特性.
故选:B.
【名师点评】此题主要考查了平行四边形的特性是容易变形.
8.B
【思路分析】因为长方形是特殊的平行四边形,所以具备平行四边形的特征:即对边平行且相等;据此解答.
【解答】解:根据长方形的性质可得:长方形中有两组对边分别平行;
故选:B.
【名师点评】明确长方形具备平行四边形的特征,是解答此题的关键.
9.C
【思路分析】根据“在两条平行线之间的线段中,垂直两条平行线的线段最短,这条线段的长叫做平行线之间的距离”即可进行选择.
【解答】解:据分析可知:两条平行线之间垂线段最短;
故选:C.
【名师点评】此题考查了垂直和平行的特征和性质,注意基础知识的灵活运用.
10.A
【思路分析】根据平行的性质:过直线外一点,画已知直线的平行线,只能画一条;据此解答即可.
【解答】解:根据平行的性质可知:过直线外一点可以画一条直线与已知直线平行,
故选:A.
【名师点评】此题考查了平行的性质,注意基础知识的积累和运用.
二.填空题(共12小题)
11.见试题解答内容
【思路分析】(1)长方形也是特殊的平行四边形,所以由图形可知:单个的小长方形有2个,2个长方形拼成的长方形有1个,共有平行四边形2+1=3个;
(2)由两个小三角形组成的梯形有2个,由3个小三角形组成的梯形有4个,由4个小三角形组成的梯形有2个,由5个小三角形组成的梯形有2个,由6个小三角形组成的梯形有1个,所以共有2+4+2+2+1=11个.
【解答】解:根据题干分析可得,平行四边形一共有2+1=3(个),
梯形有2+4+2+2+1=11(个),
故答案为:3,11.
【名师点评】考查了图形的计数,在图形的计数时,应注重一定的顺序计数,做到不遗漏,不重复.
12.见试题解答内容
【思路分析】根据平行四边形高的含义:在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高;据此解答即可.
【解答】解:从平行四边形一条边上的任意一点到对边引一条垂线,这点和垂足之间的距离叫做平行四边形的高
故答案为:垂线,高.
【名师点评】此题考查了平行四边形高的含义,应注意灵活运用.
13.见试题解答内容
【思路分析】根据平行线的定义,在同一平面内,不相交的两条直线叫做平行线,在同一平面内与一条直线互相平行的直线有无数条;据此解答.
【解答】解:在同一平面内与一条已知直线平行的直线有 无数条;
故答案为:无数.
【名师点评】此题考查了平行的特征及性质,应注意基础知识的积累.
14.见试题解答内容
【思路分析】根据长方形、平行四边形和梯形的含义及特征:两组对边分别平行,有四个直角的四边形是长方形;只有一组对边平行的四边形是梯形;两组对边分别平行的四边形是平行四边形;由此进行解答即可.
【解答】解:①两组对边分别平行,有四个直角,是长方形;
②只有一组对边平行的四边形是梯形;
③两组对边分别平行,没有直角的四边形是平行四边形;
故选:B,D,C.
【名师点评】明确长方形、平行四边形和梯形的含义及特征,是解答此题的关键.
15.
50。
【思路分析】把三角板一直角边与MN重合,左、右滑动三角板,当点P落在三角板的另一直角边时,沿这条直角边作直线,向已知线段MN画直线即可;量角要注意:量角器的中心和角的顶点对齐,角的一边与量角器的0刻度线重合。
【解答】解:作图如下:
量得∠M的度数是50度。
故答案为:50。
【名师点评】本题考查了学生垂线的作法和量角,培养学生的作图能力。
16.见试题解答内容
【思路分析】根据平行四边形高的含义:从平行四边形一条边上的一点到它的对边引一条垂线,这一点和垂足之间的距离,即平行四边形的高;每一个顶点所对的边有两条,所以平行四边形的一个顶点可以向对边作2条高(如图);进而解答即可.
【解答】解:如图,可以作2条高:
故答案为:2.
【名师点评】此题应根据平行四边形高的含义进行分析、解答.
17.1;3。
【思路分析】(1)直线没有端点,所以图中只有一条直线;
(2),如图所示,互相平行的有:AB∥CD,AD∥BC,EF∥BD,共三组平行线。
【解答】解:(1)因为直线没有端点,所以有 1条直线;
(2),如左图所示,AB∥CD,AD∥BC,EF∥BD,所以有3组平行线。
故答案为:1;3。
【名师点评】解决本题的关键在于知道直线的特点及平行的特点。
18.见试题解答内容
【思路分析】利用定理“在同一平面内,经过直线外一点有且只有一条直线与已知直线垂直”解答即可.
【解答】解:在一个平面内,过直线外一点只能画一条直线与已知直线垂直;
故答案为:一.
【名师点评】熟记“在同一平面内,经过直线外一点有且只有一条直线与已知直线垂直”是解答本题的关键.
19.见试题解答内容
【思路分析】根据垂直的定义:如果两条直线相交成直角,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫做垂足;据此解答即可.
【解答】解:如果两条直线相交成90度时,这两条直线叫做互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫做垂足.
故答案为:90,垂线,垂足.
【名师点评】此题考查了垂直与垂足的定义.
20.见试题解答内容
【思路分析】根据平行四边形的含义:有两组对边分别平行的四边形叫做平行四边形;由此解答即可.
【解答】解:两组对边分别平行的四边形叫做平行四边形;
故答案为:分别平行.
【名师点评】本题考查了平行四边形的概念,注意基础知识的积累.
21.见试题解答内容
【思路分析】依据长方形的特征及性质可知:长方形有两组互相平行的线段,有四组互相垂直的线段,据此解答即可.
【解答】解:在一个长方形中,互相平行的线段有2组,互相垂直的有4组.
故答案为:2,4.
【名师点评】此题主要考查长方形的特征及性质.
22.见试题解答内容
【思路分析】正方形是特殊的平行四边形,根据正方形的特征:四条边都相等,四个角都是直角,可知正方形相邻的两条边互相垂直,相对的两边互相平行;据此解答.
【解答】解:正方形中相邻两条边相互垂直,相对两条边相互平行;
故选:垂直,平行.
【名师点评】此题主要考查了垂直和平行的特征及性质,用到的知识点:正方形的特征.
三.判断题(共8小题)
23.×
【思路分析】根据垂线的性质:过一点有且只有一条直线与已知直线垂直,判断即可得出答案。
【解答】解:从直线外一点,向这条直线可以作有且只有一条直线与已知直线垂直。
故答案为:×。
【名师点评】考查垂线的性质。注意理解和掌握。
24.√
【思路分析】根据平行四边形的特征:对边分别平行且长度相等;进而判断即可.
【解答】解:根据平行四边形的特征可知:平行四边形的两组对边不但平行,而且长度相等;
故答案为:√.
【名师点评】此题考查了平行四边形的特征.
25.√
【思路分析】四条边都相等的是正方形;也就是说:正方形的两组对边分别平行,它是特殊的平行四边形;由此解答即可.
【解答】解:正方形的两组对边分别平行,说法正确;
故答案为:√.
【名师点评】此题应根据正方形的特征进行解答.
26.√
【思路分析】平行四边形:两组对边分别平行的四边形;梯形:只有一组对边平行的四边形,它们是两种不同的四边形,由此判断。
【解答】解:
平行四边形和梯形是两种不同的四边形,原题说法正确。
故答案为:√。
【名师点评】此题根据平行四边形、梯形的特征进行解答即可。
27.×
【思路分析】根据平行四边形的对角相等,内角和等于360°,但应该考虑特殊的平行四边形(长方形和正方形)。
【解答】解:长方形和正方形是特殊的平行四边形,长方形和正方形的四个角都是直角,所以说”平行四边形有2个锐角和2个钝角“,说法是错误的。
故答案为:×。
【名师点评】熟练掌握平行四边形的特征,是解答此题的关键。
28.√
【思路分析】梯形两底间的距离叫做梯形的高。
【解答】解:由分析可知:梯形的高与上底和下底互相垂直,所以题干的说法是正确的。
故答案为:√。
【名师点评】本题是考查作梯形的高的意义。
29.见试题解答内容
【思路分析】根据平行线的定义:在同一平面内不相交的两条直线叫做平行线;据此解答即可.
【解答】解:因为在同一平面内不相交的两条直线叫做平行线;
所以上面的说法是错误的.
故答案为:×.
【名师点评】此题考查了平行线的定义.
30.见试题解答内容
【思路分析】正方形的特征:有4条边,4条边长度相等,4个角,都是直角;据此可知正方形的对边互相平行,相邻的两条边互相垂直.
【解答】解:正方形中,相邻的两条边都互相垂直;
故答案为:√.
【名师点评】此题考查正方形的特征,也考查了垂直的意义.
四.操作题(共3小题)
31.见试题解答内容
【思路分析】梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高.
【解答】解:画出下面梯形的高(红色虚线).
【名师点评】本题是考查作梯形的高.注意作高用虚线,并标出垂足.
32.
【思路分析】把三角板一直角边与直线重合,左、右滑动三角板,当点A落在三角板的另一直角边时,这A点沿这条直角边,向已知直线画直线即可;把三角板任一边与直线重合,另边紧靠一直尺,沿直尺滑动三角板,当与直线重合的一边结过点A时,没这边画直线,所画直线就是过A点已知直线的平行线。
【解答】解:根据题意作图如下:
【名师点评】本题考查了学生垂线的作法和平行线的作法,培养学生的作图能力。
33.
【思路分析】解:先画直角梯形的高,然后在高的两端分别取直角向同一侧画出上底和下底,最后将上底和下底末端连起来成为梯形的另一条腰。
【解答】解:画图如下:
【名师点评】此题重点考查梯形的认识及作图能力。
五.应用题(共6小题)
34.200米。
【思路分析】根据平行四边形的周长=两邻边的和×2,求出周长,再乘4即可。
【解答】解:(15+10)×2×4
=25×2×4
=200(米)
答:她一共走了200米。
【名师点评】熟练掌握平行四边形的周长公式,是解答此题的关键。
35.12厘米;12厘米。
【思路分析】由题意可知,若将上底延长4厘米,则该梯形就能变成一个正方形,那么下底就是8+4=12(厘米),高也是12厘米,据此解答即可。
【解答】解:8+4=12(厘米)
答:这个梯形的下底和高都是12厘米。
【名师点评】该梯形就能变成一个正方形,这是解答此题的关键条件。
36.见试题解答内容
【思路分析】这两个梯形的周长之和比原来平行四边形的周长多了两个4厘米,据此解答即可。
【解答】解:4+4=8(厘米)
答:这两个梯形的周长之和比原来平行四边形的周长长8厘米。
【名师点评】能找出这两个梯形的周长之和与原来平行四边形的周长的关系,是解答此题的关键。
37.8厘米。
【思路分析】先算出平行四边形的周长。再求梯形的上底长即可。
【解答】解:(10+6)×2
=16×2
=32(厘米)
32﹣6×2﹣12
=32﹣12﹣12
=8(厘米)
答:上底是8厘米。
【名师点评】熟练掌握平行四边形的对边相等的性质,是解答此题的关键。
38.见试题解答内容
【思路分析】本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来路程之和最短,因为两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(如图):
【解答】解:用直线把甲村、乙村连起来.因为甲村乙村在公路的两侧,
所以这条连线必与公路AB有一个交点,
设这个交点为P,那么在P点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短.
【名师点评】两点之间的距离,线段最短,根据此性质解决问题.
39.22200元。
【思路分析】把已知的这三条边的长度相加即能求出铁栅栏的长度,再用铁栅栏的长度乘每米铁栅栏需要的钱数即可求解。
【解答】解:(120+90+160)×60
=370×60
=22200(元)
答:围这三面铁栅栏需要22200元钱。
【名师点评】本题考查了梯形周长的意义和计算方法的应用。
21世纪教育网(www.21cnjy.com)
