6.4.3.1 余弦定理 课件(共17张PPT)
文档属性
| 名称 | 6.4.3.1 余弦定理 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-03 10:24:37 | ||
图片预览




文档简介
(共17张PPT)
6.4.3.余弦定理
做数学的艺术在于找到一个特例,其中隐含了所有推广的胚芽。——大卫·希尔伯特
6.4 平面向量的应用
授课人:丁俊雅
素养目标 学科素养
1.了解余弦定理的推导过程 2.掌握余弦定理的几种变形公式及应用 3.能利用余弦定理求解三角形的边、角等问题 1.数学运算
2.数学抽象
3.逻辑推理
学习目标
问题1:初中数学学习中,判定三角形全等的方法有哪些?
初中判定三角形全等的方法有:SSS SAS ASA AAS HL.
问题2:为什么这些方法可以判断全等呢?
因为这些方法能够唯一确定三角形的形状和大小。
复习旧知
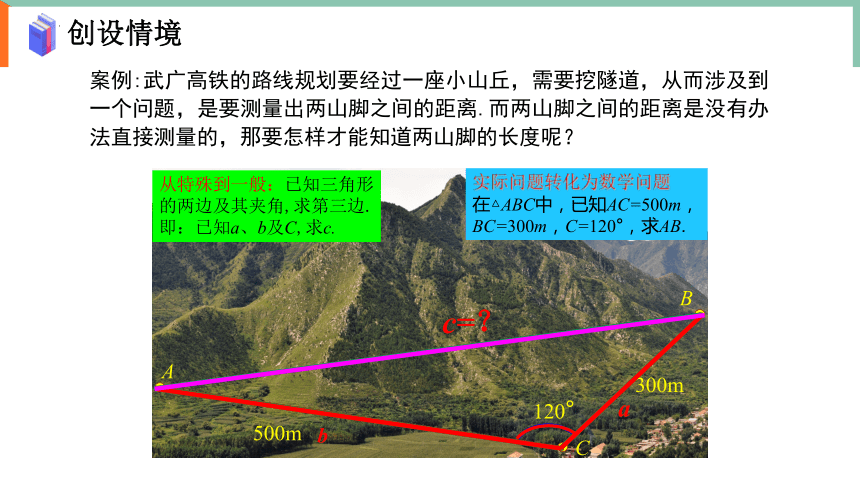
案例:武广高铁的路线规划要经过一座小山丘,需要挖隧道,从而涉及到一个问题,是要测量出两山脚之间的距离.而两山脚之间的距离是没有办法直接测量的,那要怎样才能知道两山脚的长度呢?
A
B
C
500m
120°
实际问题转化为数学问题
在△ABC中,已知AC=500m,BC=300m,C=120°,求AB.
300m
b
a
c=?
从特殊到一般:已知三角形的两边及其夹角,求第三边.即:已知a、b及C,求c.
创设情境
高中数学
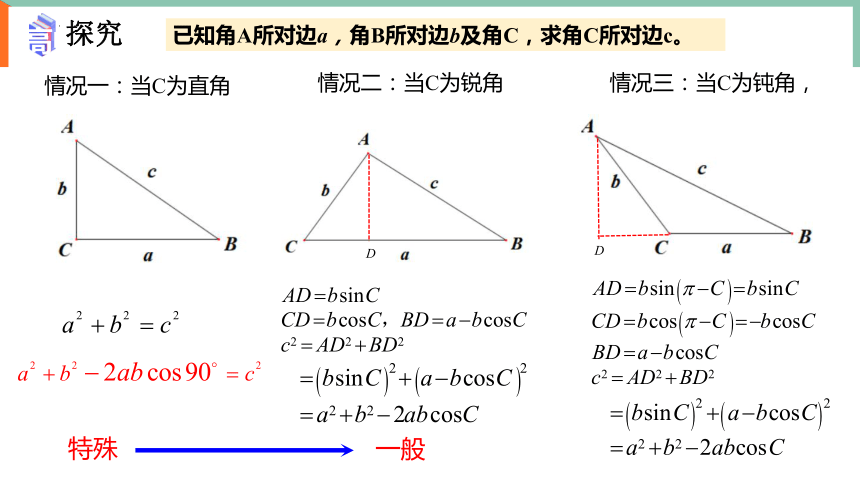
情况一:当C为直角
情况二:当C为锐角
情况三:当C为钝角,
探究
已知角A所对边a,角B所对边b及角C,求角C所对边c。
特殊
一般
三角形中任何一边的平方,等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
符号语言:
(余弦定理适用于任何三角形)
1.余弦定理
文字语言:
c
b
a
新知生成
思考:余弦定理与勾股定理有什么关系?
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
当C=90°,由余弦定理可得
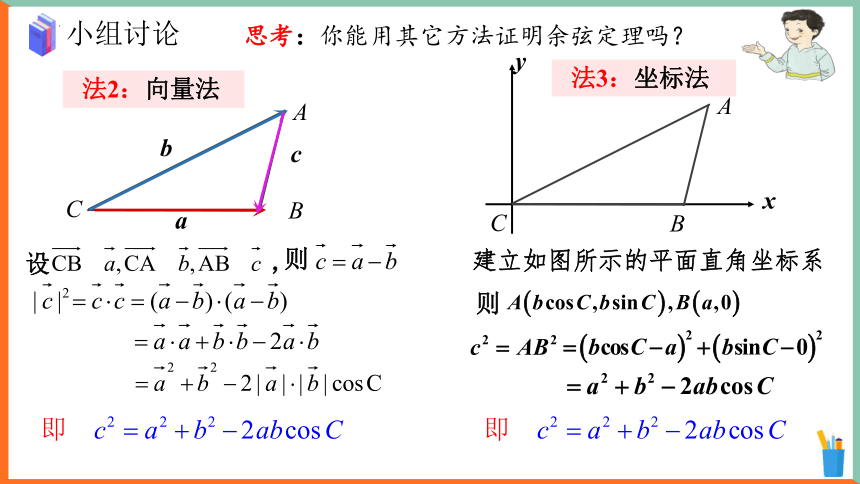
思考:你能用其它方法证明余弦定理吗?
小组讨论
y
x
b
a
c
法2:向量法
法3:坐标法
设 ,
则
建立如图所示的平面直角坐标系
则
2.余弦定理的推论
已知三条边求任意角
(SSS)
已知两边夹一角求第三边
(SAS)
问题3 利用余弦定理可以解决三角形的哪类问题?
探究
角A的对边边长:a
角B的对边边长:b
角C的对边边长:c
把三角形的三个角A,B,C和它们的对边边长a,b,c叫三角形的元素.
已知三角形的几个元素求其他元素的过程叫做解三角形.
“解三角形”的含义
解:令AC=b,BC=a,AB=c
c = a +b -2abcosC
=300 +500 -2×300×500×cos120°
=490000
所以 AB=c=700(m)
实际问题转化为数学问题
例1 在△ABC中,已知AC=500m,BC=300m,C=120°,求AB.
A
B
C
500m
120°
300m
b
a
c=?
从特殊到一般:已知三角形的两边及其夹角,求第三边.即:已知a、b及C,求c. (SAS型)
由余弦定理,得
学以致用
解:由余弦定理得
例2 在△ABC中,a= 5 ,b=2,c= ,求角C.
b= 2
c=
a= 5
()
学以致用
应用二:已知三条边求任意角(SSS)
问题4 如何利用余弦定理判断角的类型,直角、锐角还是钝角
探究
快快做笔记
学以致用
例3 在 中,内角 , , 的对边分别为 , , ,若 ,
则 ( )
A.一定是锐角三角形 B.一定是直角三角形
C.一定是钝角三角形 D.是锐角或直角三角形
C
应用三:利用余弦定理判断三角形的形状
C
在△ABC中,a=7,b=5,c=3,判断△ABC的形状为( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不确定
巩固练习
这节课你的收获是什么 请填一填.
余弦定理 文字表述 三角形中任何一边的平方,等于 减去这两边与它们的 的两倍.
公式表达 a2= ,cosA= ,
b2= ,cosB= ,
c2= . cosC= ,
应用 判断三角形的形状:
c2=a2+b2 C为 ;c2>a2+b2 C为 ;
c2解三角形:(1)已知三条边,求 ;
(2)已知两边及其夹角,求_____________________.
其他两边的平方的和
夹角的余弦的积
b
c
a
直角
钝角
锐角
三角
课堂小结
第三边和其他两个角
在△ABC中,若a=2bcosC,判断△ABC的形状.
思考:
思考
课后作业
基础巩固:
1.已知三角形的两边分别为5和6,夹角为45°,求第三边。
2.已知三角形的三边分别为5、12、13,判断其形状。
能力提升:
1.已知三角形的两边分别为7和9,夹角为60°,求第三边及最大角的余弦值。
2.已知三角形的三边分别为8、15、17,求最小角的余弦值。
综合运用:
1.某人在A点测得山峰的仰角为30°,向山峰方向行走100米后,测得仰角为45°,求山峰的高度。
2.在△ABC中,已知a=7,b=5,c=3,判断△ABC的形状,并求其面积。
6.4.3.余弦定理
做数学的艺术在于找到一个特例,其中隐含了所有推广的胚芽。——大卫·希尔伯特
6.4 平面向量的应用
授课人:丁俊雅
素养目标 学科素养
1.了解余弦定理的推导过程 2.掌握余弦定理的几种变形公式及应用 3.能利用余弦定理求解三角形的边、角等问题 1.数学运算
2.数学抽象
3.逻辑推理
学习目标
问题1:初中数学学习中,判定三角形全等的方法有哪些?
初中判定三角形全等的方法有:SSS SAS ASA AAS HL.
问题2:为什么这些方法可以判断全等呢?
因为这些方法能够唯一确定三角形的形状和大小。
复习旧知
案例:武广高铁的路线规划要经过一座小山丘,需要挖隧道,从而涉及到一个问题,是要测量出两山脚之间的距离.而两山脚之间的距离是没有办法直接测量的,那要怎样才能知道两山脚的长度呢?
A
B
C
500m
120°
实际问题转化为数学问题
在△ABC中,已知AC=500m,BC=300m,C=120°,求AB.
300m
b
a
c=?
从特殊到一般:已知三角形的两边及其夹角,求第三边.即:已知a、b及C,求c.
创设情境
高中数学
情况一:当C为直角
情况二:当C为锐角
情况三:当C为钝角,
探究
已知角A所对边a,角B所对边b及角C,求角C所对边c。
特殊
一般
三角形中任何一边的平方,等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
符号语言:
(余弦定理适用于任何三角形)
1.余弦定理
文字语言:
c
b
a
新知生成
思考:余弦定理与勾股定理有什么关系?
勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.
当C=90°,由余弦定理可得
思考:你能用其它方法证明余弦定理吗?
小组讨论
y
x
b
a
c
法2:向量法
法3:坐标法
设 ,
则
建立如图所示的平面直角坐标系
则
2.余弦定理的推论
已知三条边求任意角
(SSS)
已知两边夹一角求第三边
(SAS)
问题3 利用余弦定理可以解决三角形的哪类问题?
探究
角A的对边边长:a
角B的对边边长:b
角C的对边边长:c
把三角形的三个角A,B,C和它们的对边边长a,b,c叫三角形的元素.
已知三角形的几个元素求其他元素的过程叫做解三角形.
“解三角形”的含义
解:令AC=b,BC=a,AB=c
c = a +b -2abcosC
=300 +500 -2×300×500×cos120°
=490000
所以 AB=c=700(m)
实际问题转化为数学问题
例1 在△ABC中,已知AC=500m,BC=300m,C=120°,求AB.
A
B
C
500m
120°
300m
b
a
c=?
从特殊到一般:已知三角形的两边及其夹角,求第三边.即:已知a、b及C,求c. (SAS型)
由余弦定理,得
学以致用
解:由余弦定理得
例2 在△ABC中,a= 5 ,b=2,c= ,求角C.
b= 2
c=
a= 5
()
学以致用
应用二:已知三条边求任意角(SSS)
问题4 如何利用余弦定理判断角的类型,直角、锐角还是钝角
探究
快快做笔记
学以致用
例3 在 中,内角 , , 的对边分别为 , , ,若 ,
则 ( )
A.一定是锐角三角形 B.一定是直角三角形
C.一定是钝角三角形 D.是锐角或直角三角形
C
应用三:利用余弦定理判断三角形的形状
C
在△ABC中,a=7,b=5,c=3,判断△ABC的形状为( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不确定
巩固练习
这节课你的收获是什么 请填一填.
余弦定理 文字表述 三角形中任何一边的平方,等于 减去这两边与它们的 的两倍.
公式表达 a2= ,cosA= ,
b2= ,cosB= ,
c2= . cosC= ,
应用 判断三角形的形状:
c2=a2+b2 C为 ;c2>a2+b2 C为 ;
c2
(2)已知两边及其夹角,求_____________________.
其他两边的平方的和
夹角的余弦的积
b
c
a
直角
钝角
锐角
三角
课堂小结
第三边和其他两个角
在△ABC中,若a=2bcosC,判断△ABC的形状.
思考:
思考
课后作业
基础巩固:
1.已知三角形的两边分别为5和6,夹角为45°,求第三边。
2.已知三角形的三边分别为5、12、13,判断其形状。
能力提升:
1.已知三角形的两边分别为7和9,夹角为60°,求第三边及最大角的余弦值。
2.已知三角形的三边分别为8、15、17,求最小角的余弦值。
综合运用:
1.某人在A点测得山峰的仰角为30°,向山峰方向行走100米后,测得仰角为45°,求山峰的高度。
2.在△ABC中,已知a=7,b=5,c=3,判断△ABC的形状,并求其面积。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
