四年级暑假新课预习提升练专项练习检测卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版
文档属性
| 名称 | 四年级暑假新课预习提升练专项练习检测卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 984.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-03 21:04:20 | ||
图片预览


文档简介
四年级暑假新课预习提升练专项练习检测卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版
学校:___________姓名:___________班级:___________考号:___________
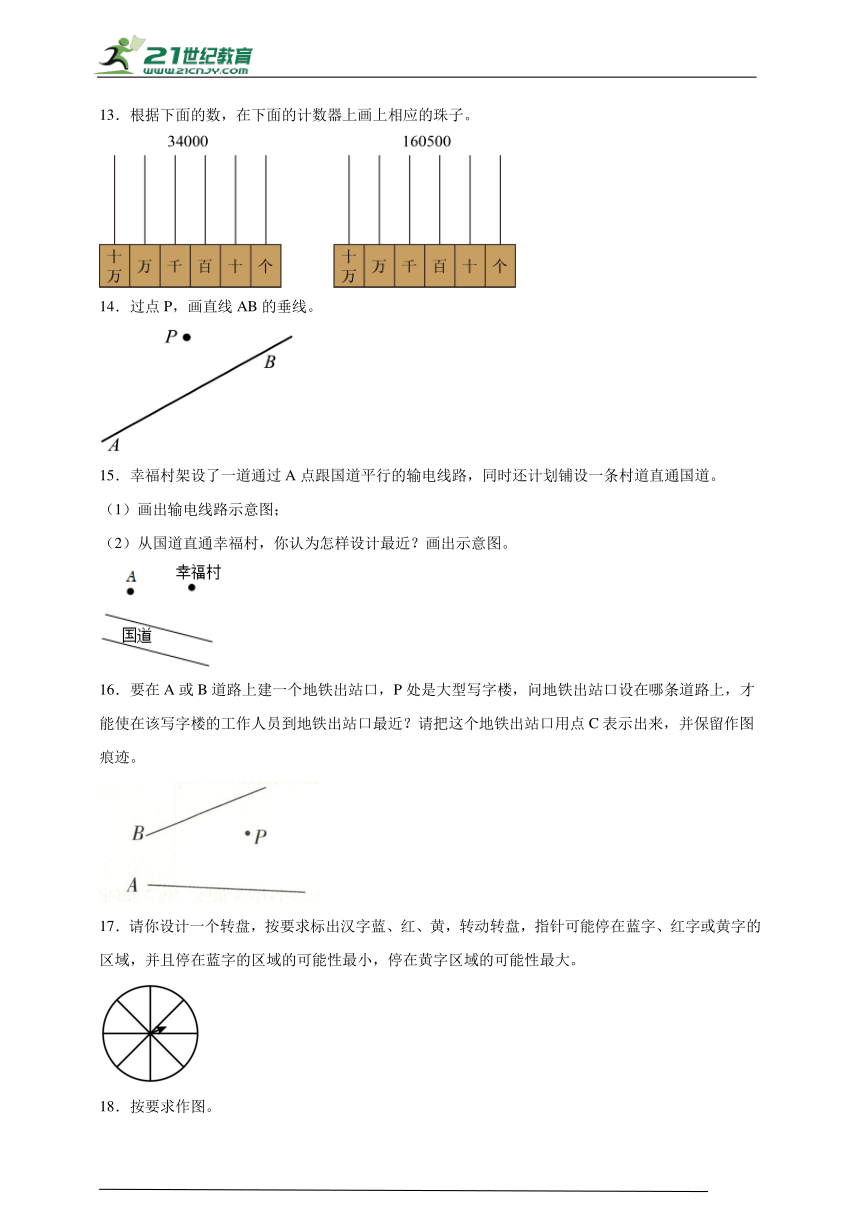
一、作图题
1.画出线段AB,射线BC和直线AC。
2.先描出A(1,1),B(4,1),C(2,3)各点,并依次连成封闭图形,再将这个图形向右平移4格,并画出来。
3.按要求画一画。
(1)商场东面50米的地方有一个书报亭,请你用★标出它的位置。
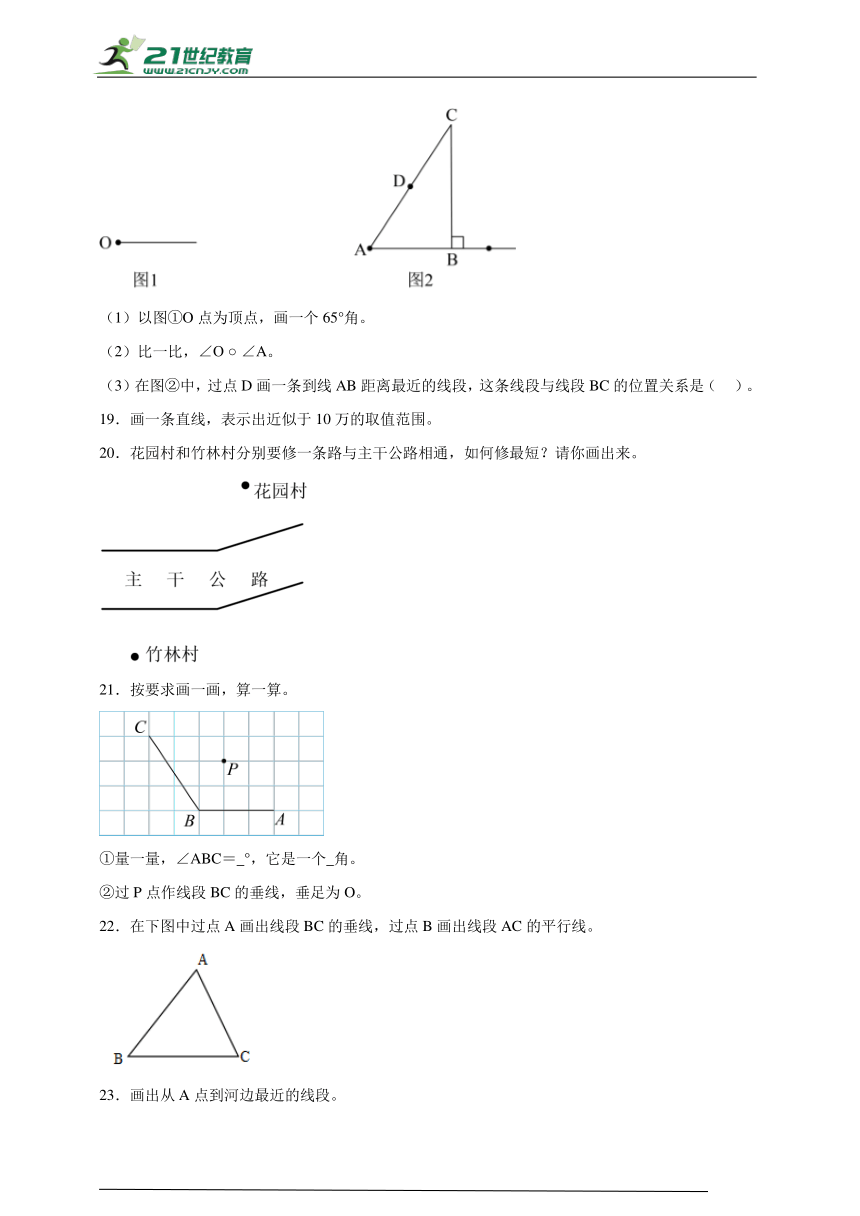
(2)书报亭北面60米的地方有一个公园,请你用▲标出它的位置。
4.在图上标出94000000、1亿、105000000。
5.画出下面各角,并说出它们分别是哪种角。
45° 90° 130°
6.以给出的射线的端点为顶点,画一个125°的角。
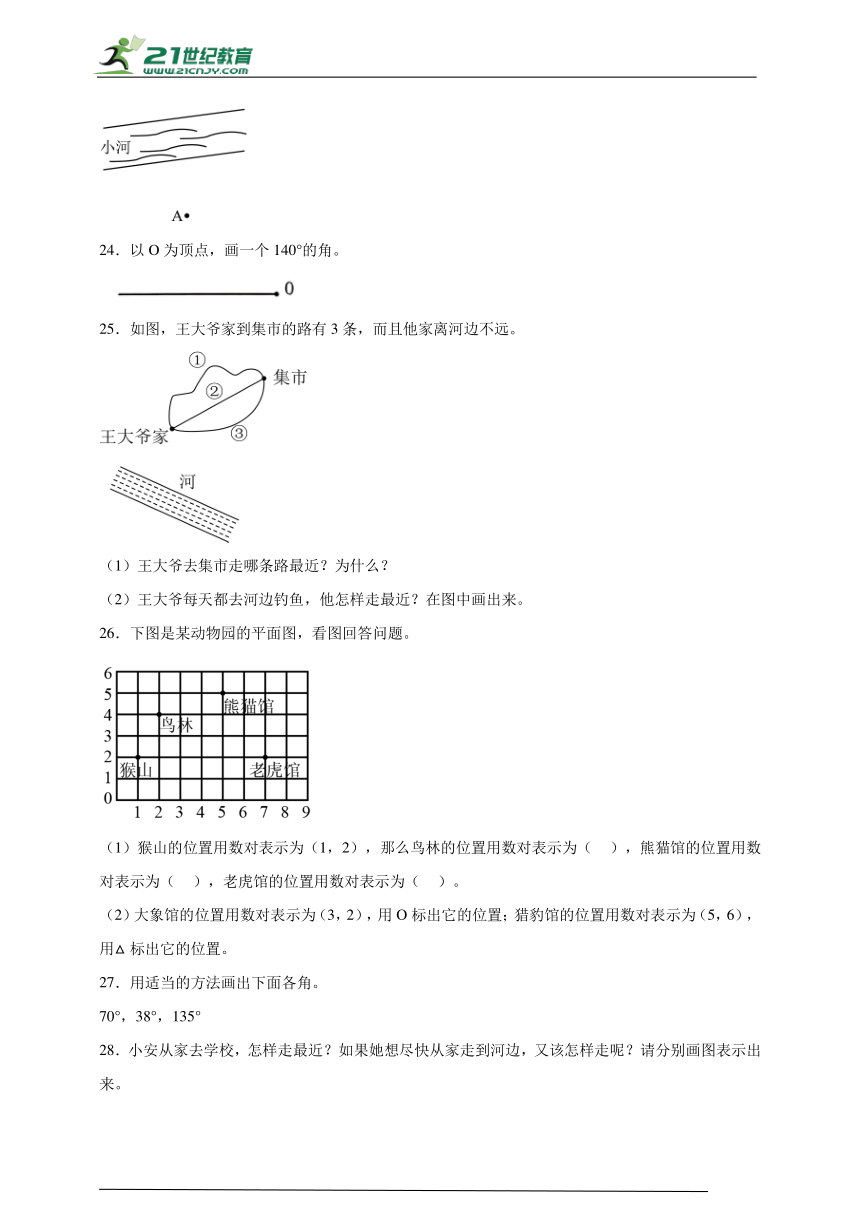
7.标一标,画一画。
在花园小区的东边70米的地方有一所中学,西边30米的地方有一家超市;在超市南边20米的地方是中心广场。请你用标出中学的位置,用标出超市的位置,用☆标出中心广场的位置。
8.过P点作OB边的平行线,过P点作OA边的垂直线。
9.
(1)超市东面30米处有一个书店,请用“”标出它的位置,超市西面50米有一个电影院,请用“”标出它的位置。
(2)书店北面20米处有一所学校,请用“”标出它的位置。
10.先画射线AC,再以A为顶点,AC为边,画80°的角。
11.李叔叔要挖一条引水渠把河里的水引到饲养场,怎样设计可以使水渠最短?在图中画一画。
12.按要求画一画。
(1)画直线AB。
(2)画射线AD。
(3)过点C作直线AB的平行线。
(4)过点D作直线AB的垂线。
13.根据下面的数,在下面的计数器上画上相应的珠子。
14.过点P,画直线AB的垂线。
15.幸福村架设了一道通过A点跟国道平行的输电线路,同时还计划铺设一条村道直通国道。
(1)画出输电线路示意图;
(2)从国道直通幸福村,你认为怎样设计最近?画出示意图。
16.要在A或B道路上建一个地铁出站口,P处是大型写字楼,问地铁出站口设在哪条道路上,才能使在该写字楼的工作人员到地铁出站口最近?请把这个地铁出站口用点C表示出来,并保留作图痕迹。
17.请你设计一个转盘,按要求标出汉字蓝、红、黄,转动转盘,指针可能停在蓝字、红字或黄字的区域,并且停在蓝字的区域的可能性最小,停在黄字区域的可能性最大。
18.按要求作图。
(1)以图①O点为顶点,画一个65°角。
(2)比一比,∠O ○ ∠A。
(3)在图②中,过点D画一条到线AB距离最近的线段,这条线段与线段BC的位置关系是( )。
19.画一条直线,表示出近似于10万的取值范围。
20.花园村和竹林村分别要修一条路与主干公路相通,如何修最短?请你画出来。
21.按要求画一画,算一算。
①量一量,∠ABC= °,它是一个 角。
②过P点作线段BC的垂线,垂足为O。
22.在下图中过点A画出线段BC的垂线,过点B画出线段AC的平行线。
23.画出从A点到河边最近的线段。
24.以O为顶点,画一个140°的角。
25.如图,王大爷家到集市的路有3条,而且他家离河边不远。
(1)王大爷去集市走哪条路最近?为什么?
(2)王大爷每天都去河边钓鱼,他怎样走最近?在图中画出来。
26.下图是某动物园的平面图,看图回答问题。
(1)猴山的位置用数对表示为(1,2),那么鸟林的位置用数对表示为( ),熊猫馆的位置用数对表示为( ),老虎馆的位置用数对表示为( )。
(2)大象馆的位置用数对表示为(3,2),用O标出它的位置;猎豹馆的位置用数对表示为(5,6),用△标出它的位置。
27.用适当的方法画出下面各角。
70°,38°,135°
28.小安从家去学校,怎样走最近?如果她想尽快从家走到河边,又该怎样走呢?请分别画图表示出来。
29.画一画。
在下面方格纸上画出一组平行线。
30.量出下面各个角的度数。
31.操作。
(1)请你画出从教学楼到实验室最近的路。
(2)请你画出从教学楼到操场最近的路。
32.画一条直线与已知直线平行。
33.在数线图上标出三个数:950万、1000万、895万。
34.过点A画已知直线的平行线。
35.过直线外一点O画已知直线AB的垂线和平行线。
36.过A点做下面直线的垂线和平行线。
37.过O点分别作出直线AB的平行线和直线CD的垂线。
38.一个游泳池,四条岸边正好围成一个长方形,其中的两条岸边已标出。
(1)请将游泳池另外两条岸边补充完整。
(2)乐乐在游泳池里游泳,目前他在处,他想尽快游上岸。请你帮他设计一条游上岸的路线,在图上画出来。
39.画一条3厘米长的线段AB,以A为顶点,画一个65°的角,再画线段AB的一条垂线。
40.利用三角尺、直尺,过点C作直线AB的平行线。
41.以点O为顶点,画一个135°的角,并标出角的度数。
42.过M点作直线AB的平行线和垂线。
43.草地上有一只小羊,小羊想去河边喝水,请你画出小羊走到河边最近的路线。
44.分别画一个110°、60°的角。
45.画直线l的垂线。
46.以O为顶点,用量角器画一个120°的角,并标出角的度数。
47.用量角器分别画出30°、115°、140°和170°的角。
48.用学过的画垂线和平行线的方法把长方形画完整。
49.以点O为顶点,画一个136°的角。
50.分别用三角板和量角器两种方法画一个的角。
《四年级暑假新课预习提升练专项练习检测卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版》参考答案
1.见详解
【分析】(1)线段有两个端点,不能向两端延伸,据此连接AB,即可得到线段AB;
(2)射线只有一个端点,只能向一端无限延伸,不能量出长度,据此连接BC并向C点的一端延长,即可画出射线BC;
(3)直线没有端点,可以向两端无限延伸,不能量出长度,据此连接AC并向两端延长,即可画出直线AC。
【详解】作图如下:
2.见详解
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可在图中描出各点,并依次连成封闭图形。根据平移的特征,把这个图形的各顶点分别向右平移4格,依次连接即可得到向右平移4格后的图形。图形的形状和大小不变,只是图形的位置发生了变化。
【详解】据分析作图如下:
3.(1)见详解;(2)见详解
【分析】(1)图中1格表示10米,书报亭在商场东面,即商场的右面,距离是50米,即距离5格,据此标出书报亭的位置;
(2)公园在书报亭的北面,且距离是60米,即从书报亭向上6格的位置,即为公园的位置。
【详解】
(1)(2)
4.见详解
【分析】观察数轴,每个单位长度表示100万,100万100万地数,从9000万数4个百万是94000000,从9000万数10个百万是1亿,从1亿数5个百万是105000000。
【详解】
【点睛】此题考查的是大数在数轴上的表示。
5.见详解
【分析】画角:画一条射线用量角器的中心和射线的端点重合,0刻度线和射线重合,从射线端的0刻度线开始,数到要画的度数,在度数的刻度处点上一个小圆点。从射线的端点起,过刚才画好的小圆点画一条射线。最后再标注上角的符号和度数。
锐角度数大于0度小于90度;直角度数等于90度;钝角度数大于90度小于180度。
【详解】
【点睛】明确角的分类及角的画法是解决本题关键。
6.具体画法见详解
【分析】使量角器的中心与给出的射线的端点重合,0刻度线与给出的射线重合。再在量角器上对准要画角的度数的刻度线,并点上一点。然后以已画出的射线的端点为端点,通过刚画的点,再画一条射线,这两条射线所成的夹角就是所要画的角度。据此画一个125°的角。
【详解】具体画法如图所示:
7.见详解
【分析】由题目可知,根据利用方向和距离确定物体位置的方法,先确定方向,再确定距离。通过观察图形可知,图中每格表示10米,从花园小区往西数3格就是超市的位置,从花园小区往东数7格就是中学的位置,从超市往南数2格就是中心广场,据此作图即可。
【详解】如图:
8.见详解
【分析】把直角三角尺的一条直角边与OB重合,使得点P在直角三角尺的另一条直角边上,将直尺紧靠这条直角边,沿着直尺的边过点P画直线即为OB的平行线;把直角三角尺的一条直角边与OA重合,使得点P在直角三角尺的另一条直角边上,沿着直角三角尺的这条直角边过点P向OA作直线即为OA边的垂线。
【详解】
【点睛】考查学生借助直角三角尺以及直尺作已知直线的平行线与垂线的方法。
9.见详解
【分析】图中方向已给出,可知一格代表10米, 30米即为3格,50米即为5格,20米即为2格,据此画图即可。
【详解】
10.见详解
【分析】射线只有一个端点,因此以点A为端点过C点画一条直的线,即可得到射线AC;
使量角器的中心和射线的A点重合,0°刻度线和射线AC重合,然后在量角器80°刻度线的地方点一个点,最后以画出的射线的端点为端点,通过刚画的点,再画一条射线;依此画图并标上对应的度数即可。
【详解】画图如下:
【点睛】解答此题的关键是要熟练掌握射线的特点,以及应掌握用量角器画角的方法。
11.见详解
【分析】直线外一点到直线上各点的连线中,垂线段最短,从饲养场作小河的垂线段,沿垂线段挖可以使水渠最短。
【详解】
【点睛】本题主要考查学生对垂线的特征及性质的掌握和灵活运用。
12.见详解
【分析】(1)根据直线没有端点,无限延长,画直线AB。
(2)根据射线只有一个端点,无限延长,画射线AD。
(3)把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和C点重合,过C点沿三角板的直角边,向已知直线画直线即可。
(4)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和D点重合,过D点沿三角板的直角边画直线即可。
【详解】(1)(2)(3)(4)如图:
13.见详解
【分析】用计数器表示数字时,哪个数位上是几,就在那个数位上拨几个珠子。
34000,这个数的千位是4,拨4个珠子,万位是3,拨3个珠子,个位、十位和百位是0,不拨珠子;
160500,这个数的百位是5,拨5个珠子,万位是6,拨6个珠子,十万位是1,拨1个珠子,个位、十位和千位是0,不拨珠子。
【详解】
14.见详解
【分析】过直线上或直线外一点作垂线的步骤:
①把三角尺的一条直角边与已知直线重合;
②沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上;
③沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是已知直线的垂线。
【详解】作图如下:
15.见详解
【分析】(1)过直线外一点作直线的平行线:把三角板的一边靠紧直线,另一边靠紧一直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线就是过该点作的直线的平行线;过A点作国道的平行线即可。
(2)直线外一点到直线上各点的连线中,垂线段最短,从幸福村作国道的垂线段,沿垂线段修村道最近。
【详解】(1)(2)见下图:
【点睛】熟练掌握平行线和垂线的画法是解答本题的关键。
16.见详解
【分析】从直线外一点到这条直线所画的所有线段中,垂线段最短。所以在垂线段与直线的交点处设地铁口,才能使在该写字楼工作的人到地铁口最近。
分别过点P向道路A和道路B作垂线,并标出垂足点。经测量发现,点P与B道路的距离更近,所以地铁口应设在点C。
【详解】根据分析画图如下:
经测量发现,点P与B道路的距离更近,所以地铁口应设在点C。
17.见详解
【分析】可能性的大小与区域的大小有关,某种颜色所占的区域大则停在该区域的可能性就大,反之就小;由题意可知,转盘内有黄、红、蓝三种颜色且蓝字的区域最小,黄字区域最大。共有8个区域,则黄字区域有5个,红字区域有2个,蓝字区域有1个,据此作图即可。
【详解】如图所示:
(答案不唯一)
【点睛】本题考查可能性,明确可能性的大小与区域的大小有关是解题的关键。
18.(1)图见详解
(2)∠O > ∠A
(3)图见详解;平行
【分析】(1)画角的步骤是:使量角器的中心和O点重合,0°刻度线和已知射线重合,然后在量角器65°刻度线的地方点一个点,最后以画出的射线的端点为端点,通过刚画的点,再画一条射线;
(2)用量角器测量出∠A的度数,再比较;用量角器测量角时,量角器的中心和角的顶点重合,0刻度线和角的一边重合,另一边所指的刻度就是角的大小;
(3)从线段外一点到这条线段所画的垂直线段最短,它的长度叫作点到线段的距离;把直角三角尺的一边与线段AB重合,使得D点在另一条直角边上,过点D沿着另一条直角边画线段交AB与E点,即DE为点D到AB的距离(标上垂直符号),也就是到线AB距离最近的线段。两条直线都与第三条直线垂直,那么这两条直线也互相平行,据此解答。
【详解】(1)65°角如下图:
(2)根据分析可测量出∠A=58°,65°>58°,也就是∠O > ∠A;
(3)根据分析可画出到线AB距离最近的线段DE,如下图:
根据题意可知,线段DE和线段BC都与线段AB垂直,所以DE∥AB,也就是这条线段与线段BC的位置关系是平行。
19.见详解
【分析】省略万后面的尾数要看千位上的数,根据四舍五入法的原则,若千位上的数字大于等于5,就向万位进1;若千位上的数字小于5,就舍去千位及其后面数位上的数。据此解答即可。
【详解】“四舍”得到的10万最大,是104999;“五入”得到的10万最小,是95000。
20.见详解
【分析】直线外一点与直线上各点的连线中,垂线段最短,分别从两个村作公路的垂线段,沿垂线段修最短。
【详解】
【点睛】本题主要考查学生对垂直的特征及性质的掌握和灵活运用。
21.①120;钝
②见详解
【分析】①角的测量方法:用量角器量角时,先把量角器的中心点与角的顶点重合, 0°刻度线与角的一条边重合。角的另一条边所对的量角器上的刻度,就是这个角的度数;大于90°且小于180°的角是钝角;
②用三角板的一条直角边和已知线段BC重合,沿重合的线段平移三角板,使三角板的另一条直角边和P点重合,过P沿直角边向已知线段画垂线即可。
【详解】①通过测量可知,∠ABC=120°,120°<180°,则它是一个钝角。
②如下图:
22.见详解
【分析】过一点作直线的垂线:把三角板的一直角边靠紧直线,沿这条直线滑动三角板,当另一直角边经过该点时,沿这条直角边画的直线就是过该点作的直线的垂线;
过直线外一点作直线的平行线:把三角板的一边靠紧直线,另一边靠紧一直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线就是过该点作的直线的平行线。
【详解】
【点睛】熟练掌握垂线和平行线的画法是解答本题的关键。
23.见详解
【分析】从直线外一点到这条直线所画的垂直线段最短,它的长度叫作点到直线的距离;因此过A点作河边的垂线段即可。
过一点作已知直线的垂线:把三角板的一直角边靠紧直线,沿这条直线滑动三角板,当另一直角边经过该点时,沿这条直角边画的直线就是过该点作的直线的垂线,依此画图并标上垂直符号即可。
【详解】画图如下:
24.见详解
【分析】使量角器的中心和射线的端点重合,零刻度线和射线重合,在量角器上140度刻度线的地方点一个点,然后以射线的端点为端点,通过刚画的点,再画一条射线,这两条射线所夹的角就是140°的角。
【详解】
25.(1)第②条路最近; 因为两点之间线段最短。
(2)王大爷去河边挑水应走垂直线;见详解
【分析】(1)首先明确两点之间线段最短,王大爷去集市走第②条路最近。
(2)直线外一点到直线的线段中, 垂线段最短, 所以王大爷去河边挑水应走垂直线。从王大爷家向河边画垂线即可。
【详解】根据分析可知:
(1)王大爷去集市走第②条路最近, 因为两点之间线段最短。
(2)王大爷去河边挑水应走垂直线。画图如下:
26.(1)(2,4);(5,5);(7,2)
(2)见详解。
【分析】根据图示,结合所学知识,确定位置,先列后行,数对中第一个数表示在第几列,第二个数表示在第几行,根据这个,可以得出鸟林的位置、熊猫馆的位置和老虎馆的位置该如何表示。
【详解】(1)依题意,结合所学知识,鸟林在第二列,第四行,其位置用数对表示为(2,4),熊猫馆在第五列,第五行,其位置用数对表示为(5,5),老虎馆在第七列,第二行,其位置用数对表示为(7,2)。
(2)大象馆的位置用数对表示为(3,2),意味着其在第3列,第2行,对应位置如下图;同理可得猎豹馆的位置。如下图表示:
【点睛】本题考查学生对用数对表示位置知识的理解和掌握,学生能够熟记规则是解答的关键。
27.见详解
【分析】画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合。在量角器70°刻度线的地方点一个点。以画出的射线的端点为端点,通过刚画的点,再画一条射线。据此画出70°的角。同理画出38°和135°的角。
【详解】
28.见详解。
【分析】从家去学校,可以看成两点之间,找最短的距离,根据两点之间线段最短可以画出。从家尽快到河边,可以看成是直线外一点到之间的距离,根据垂线段最短知识可以画出。
【详解】依题意,结合所学知识,两点间线段最短,直接画线段连接小安家和学校;根据垂线段最短,可以得出从小安家画一条垂线与河边垂直即可。如下图所示:
【点睛】本题考查两点之间线段最短和垂线段最短知识,学生熟练掌握是解题的关键。
29.见详解
【分析】根据同一平面内,永不相交的两条直线叫做平行线,平行线之间的距离处处相等,先画一条线段,利用平移即可作出它的平行线,据此画图即可。
【详解】据分析作图如下:
(答案不唯一)
30.见详解
【分析】角的度量方法:用量角器量角时,先把量角器的中心与角的顶点重合, 0°刻度线与角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数;如果角的起始边不是与0刻度线重合,角的度数为两条边所对的刻度之差。
【详解】
【点睛】本题主要考查学生用量角器度量角度数方法的掌握和灵活运用。
31.(1)见详解
(2)见详解
【分析】(1)根据两点之间线段最短,将实验室与教学楼用直尺进行连线即可得到教学楼到实验室最近的路;
(2)点到直线之间,垂线段最短,因此,过教学楼一点向操场的一边作垂线与操场一边相交的点即为垂足,教学楼与垂足之间的距离即为教学楼到操场最近的路。
【详解】(1)教学楼到实验室最近的路如下图:
(2)教学楼到操场最近的路如下图:
32.见详解
【分析】用三角板的一条直角边和已知直线重合,用直尺紧靠三角板的另一条直角边,按住直尺不动,沿直尺平移三角板一段距离后,沿着这条直角边画一条直线,所画直线与已知直线平行,据此作图即可。
【详解】画一条直线与已知直线平行,如下图所示:
(答案不唯一)
【点睛】经过直线外一点有且只有一条直线与已知直线平行;因为直线外有无数点,所以有无数条直线与已知直线平行。
33.标数见详解
【分析】从图上可以看出,800万和900万之间相差100万,平均分成了10份,每份是10万;950万比900万多50万,也就是多5个10万,即在900万右边第5格处;1000万比900万多100万,也就是多10个10万,即在900万右边第10格处;895万可以看作800万加90万再加5万,先在800万右边第9格处找到890万,5万是10万的一半,即895万在890万和900万中间处;据此解答。
【详解】根据分析,标数如下:
34.见详解
【分析】把三角尺的一条直角边与已知直线重合,使得点A在三角尺的另一条直角边上,把直尺与三角尺的这条直角边重合,沿着直尺过点A画直线即为已知直线的平行线。
【详解】
【点睛】画图时借助直尺和三角尺画平行线。在同一平面内,永不相交的两条直线互相平行。
35.见详解
【分析】(1)用三角板的一条直角边的已知直线AB重合,沿重合的直线AB平移三角板,使三角板的另一条直角边和O点重合,过O点沿直角边向已知直线AB画直线即可;
(2)把三角板的一条直角边与已知直线AB重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线AB重合的直角边和O点重合,过O点沿三角板的直角边画直线即可。
【详解】据分析作图如下:
【点睛】本题主要考查了平行线和垂线的作法,培养学生的作图能力。
36.见详解
【分析】用直角三角尺的一条直角边和直线重合,移动三角尺,使三角尺的另一条直角边和点A重合,过A点沿直角边向已知直线画直线即是过A点作出的直线的垂线。把三角尺的一条直角边和已知直线重合,用直尺靠紧三角尺的另一条直角边,沿直尺移动三角尺,使三角尺原来和已知直线重合的直角边和A点重合,过A点沿三角尺的直角边画直线即是过A点作出的直线的平行线。
【详解】
【点睛】此题考查了学生用三角尺和直尺作垂线和平行线的能力。
37.见详解
【分析】把三角板的一条直角边与已知直线CD重合,沿直线移动三角板,使三角板的另一条直角边和O点重合,过O点沿三角板的直角边,向已知直线CD画直线即为其垂线。
把三角板的一条直角边与已知直线AB重合,把直尺靠紧三角板的另一条直角边,使得点O在另一条直角边上,移动直尺,沿着直尺过点O画直线即为所求平行线。
【详解】作图如下:
【点睛】本题考查了学生平行线和垂线的作法,培养学生的作图能力。
38.图见详解
【分析】(1)长方形的特征:两组对边平行且相等,有4个直角;用三角尺的直角边分别紧靠长方形的长和宽,然后平移三角尺至长(宽)的另一端点处,在三角尺的另一条直角边上,过该端点画出与之长(宽)平行且相等的线段,依此画出长方形的另外两条边即可;
(2)在同一平面内,点到直线的所有连线中,垂线段最短;显然,点M离长方形的宽比较近,因此用三角尺的直角边与长方形的宽重合,另一直角边平移至点M处,沿着直角边即可画出垂线段(不出头),最后标上直角符号即可。
【详解】根据分析作图如下:
39.见详解
【分析】沿直尺的0刻度线到3厘米刻度线画出的图形就是3厘米长的线段,标上端点和长度;使量角器的中心点和线段的端点A重合,0刻度线和线段AB重合,在量角器上找到65°度数的地方点一个点,以点A为端点,通过刚画的点,再画一条射线,组成的图形就是65°的角,在角内标上角的符号和度数;用直角三角尺的一条直角边和线段AB重合,沿另一直角边向线段AB画直线即可。
【详解】
【点睛】此题考查了学生画线段和角以及画垂线的能力。
40.见详解
【分析】过直线外一点作直线的平行线:把三角板的一条直角边靠紧直线,另一条直角边靠紧直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线就是过该点作的直线的平行线。
【详解】画图如下:
41.见详解
【分析】画角的步骤:先画一条射线,使量角器的中心和射线的端点重合,零刻度线和射线重合,在量角器上要画的角的度数刻度线的地方点一个点,然后以画出的射线的端点为端点,通过刚刚画的点,再画一条射线,这两条射线所夹的角就是我们所要画的角。
【详解】如图:
【点睛】熟练掌握用量角器画角的方法是解答本题的关键。
42.见详解
【分析】(1)过直线上或直线外一点作垂线的方法:先把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是已知直线的垂线。
(2)过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使直线外的点在三角尺上。沿直角边画出另一条直线即可。
【详解】
43.见详解
【分析】因为直线外一点与这条直线所有点的连线中,垂线段最短,所以,只要作出小羊到小河的垂线段即可。
【详解】根据垂直线段最短的性质,即可画出这条从小羊到河边最近的线路,如图所示:
【点睛】此题考查了垂直线段最短的性质的在解决实际问题中的灵活应用。
44.见详解
【分析】先画一条射线使量角器的中心和射线的端点重合,零刻度线和射线重合,在量角器所画角度刻度线的地方点一个点,以射线的端点为端点,通过刚画的点,再画一条射线即可。
【详解】
【点睛】本题考查了学生根据所给度数利用作图工具画角的动手能力。
45.见详解
【分析】用直角三角尺的一条直角边和直线重合,沿直角三角尺的另一条直角边向已知直线画直线即可。
【详解】
【点睛】此题考查了学生用三角尺作垂线的能力。
46.见详解
【分析】将量角器的中心对准O,然后将量角器的0刻度线与角的一边重合,由于O在左边,所以角的开口向右,此时观察量角器的外圈刻度,找到120°处标一点,然后连接这个点与点O即可得到一个120°的角。
【详解】
47.见详解
【分析】先确定一个端点,引出一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合;再在量角器上对准要画角的度数的刻度线,并点上一个点;然后以已画出的射线的端点为端点,通过刚画的点,再画一条射线,这两条射线所成的夹角就是所要画的角度。
【详解】
【点睛】本题主要考查学生对用量角器画角方法的掌握。
48.见详解
【分析】长方形的特征:长方形两组对边平行且相等,两条对角线相等且互相平分,长方形是特殊的平行四边形;
过直线外一点画平行线:固定三角尺,沿一条直角边先画一条直线;用直尺紧靠着三角尺的另一条直角边,固定直尺,然后沿着直尺平移三角尺;平移后,沿直角边画出另一条直线;
过直线上或直线外一点作垂线的步骤:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上;沿三角尺的另一条直角边画一条直线,并画上垂直符号;这条直线就是已知直线的垂线;据此作图。
【详解】如图:
【点睛】掌握长方形的特征,以及垂线和平行线的画法是解答本题的关键。
49.见详解
【分析】以O点为端点画一条射线,使量角器的中心点和点O重合,0刻度线和射线重合,在量角器上找到136°度数的地方点一个点,以点O为端点,通过刚画的点,再画一条射线,组成的图形就是136°的角,在角内标上角的符号和度数。
【详解】
【点睛】画角的方法可以总结为一画射线,二重合,三找点,四连线,五标度数,六检查。
50.见详解
【分析】(1)画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合,在量角器150°刻度线的地方点一个点,以画出的射线的端点为端点,通过刚画的点,再画一条射线,据此画出150°的角。
(2)用三角尺上的90°的角,画一个角,再在这个画的90°角的外部,用三角尺上的60°的角同90°的角在顶点重合,一条边重合,画出60°的角,这两个角拼成的角就是150°的角,据此解答。
【详解】根据分析,用量角器画角如下:
三角尺画角如下:
【点睛】本题考查了量角器画角的方法和用三角尺上的角进行组合画角的方法,注意用量角器时,量角器的中心和射线的端点要重合。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.画出线段AB,射线BC和直线AC。
2.先描出A(1,1),B(4,1),C(2,3)各点,并依次连成封闭图形,再将这个图形向右平移4格,并画出来。
3.按要求画一画。
(1)商场东面50米的地方有一个书报亭,请你用★标出它的位置。
(2)书报亭北面60米的地方有一个公园,请你用▲标出它的位置。
4.在图上标出94000000、1亿、105000000。
5.画出下面各角,并说出它们分别是哪种角。
45° 90° 130°
6.以给出的射线的端点为顶点,画一个125°的角。
7.标一标,画一画。
在花园小区的东边70米的地方有一所中学,西边30米的地方有一家超市;在超市南边20米的地方是中心广场。请你用标出中学的位置,用标出超市的位置,用☆标出中心广场的位置。
8.过P点作OB边的平行线,过P点作OA边的垂直线。
9.
(1)超市东面30米处有一个书店,请用“”标出它的位置,超市西面50米有一个电影院,请用“”标出它的位置。
(2)书店北面20米处有一所学校,请用“”标出它的位置。
10.先画射线AC,再以A为顶点,AC为边,画80°的角。
11.李叔叔要挖一条引水渠把河里的水引到饲养场,怎样设计可以使水渠最短?在图中画一画。
12.按要求画一画。
(1)画直线AB。
(2)画射线AD。
(3)过点C作直线AB的平行线。
(4)过点D作直线AB的垂线。
13.根据下面的数,在下面的计数器上画上相应的珠子。
14.过点P,画直线AB的垂线。
15.幸福村架设了一道通过A点跟国道平行的输电线路,同时还计划铺设一条村道直通国道。
(1)画出输电线路示意图;
(2)从国道直通幸福村,你认为怎样设计最近?画出示意图。
16.要在A或B道路上建一个地铁出站口,P处是大型写字楼,问地铁出站口设在哪条道路上,才能使在该写字楼的工作人员到地铁出站口最近?请把这个地铁出站口用点C表示出来,并保留作图痕迹。
17.请你设计一个转盘,按要求标出汉字蓝、红、黄,转动转盘,指针可能停在蓝字、红字或黄字的区域,并且停在蓝字的区域的可能性最小,停在黄字区域的可能性最大。
18.按要求作图。
(1)以图①O点为顶点,画一个65°角。
(2)比一比,∠O ○ ∠A。
(3)在图②中,过点D画一条到线AB距离最近的线段,这条线段与线段BC的位置关系是( )。
19.画一条直线,表示出近似于10万的取值范围。
20.花园村和竹林村分别要修一条路与主干公路相通,如何修最短?请你画出来。
21.按要求画一画,算一算。
①量一量,∠ABC= °,它是一个 角。
②过P点作线段BC的垂线,垂足为O。
22.在下图中过点A画出线段BC的垂线,过点B画出线段AC的平行线。
23.画出从A点到河边最近的线段。
24.以O为顶点,画一个140°的角。
25.如图,王大爷家到集市的路有3条,而且他家离河边不远。
(1)王大爷去集市走哪条路最近?为什么?
(2)王大爷每天都去河边钓鱼,他怎样走最近?在图中画出来。
26.下图是某动物园的平面图,看图回答问题。
(1)猴山的位置用数对表示为(1,2),那么鸟林的位置用数对表示为( ),熊猫馆的位置用数对表示为( ),老虎馆的位置用数对表示为( )。
(2)大象馆的位置用数对表示为(3,2),用O标出它的位置;猎豹馆的位置用数对表示为(5,6),用△标出它的位置。
27.用适当的方法画出下面各角。
70°,38°,135°
28.小安从家去学校,怎样走最近?如果她想尽快从家走到河边,又该怎样走呢?请分别画图表示出来。
29.画一画。
在下面方格纸上画出一组平行线。
30.量出下面各个角的度数。
31.操作。
(1)请你画出从教学楼到实验室最近的路。
(2)请你画出从教学楼到操场最近的路。
32.画一条直线与已知直线平行。
33.在数线图上标出三个数:950万、1000万、895万。
34.过点A画已知直线的平行线。
35.过直线外一点O画已知直线AB的垂线和平行线。
36.过A点做下面直线的垂线和平行线。
37.过O点分别作出直线AB的平行线和直线CD的垂线。
38.一个游泳池,四条岸边正好围成一个长方形,其中的两条岸边已标出。
(1)请将游泳池另外两条岸边补充完整。
(2)乐乐在游泳池里游泳,目前他在处,他想尽快游上岸。请你帮他设计一条游上岸的路线,在图上画出来。
39.画一条3厘米长的线段AB,以A为顶点,画一个65°的角,再画线段AB的一条垂线。
40.利用三角尺、直尺,过点C作直线AB的平行线。
41.以点O为顶点,画一个135°的角,并标出角的度数。
42.过M点作直线AB的平行线和垂线。
43.草地上有一只小羊,小羊想去河边喝水,请你画出小羊走到河边最近的路线。
44.分别画一个110°、60°的角。
45.画直线l的垂线。
46.以O为顶点,用量角器画一个120°的角,并标出角的度数。
47.用量角器分别画出30°、115°、140°和170°的角。
48.用学过的画垂线和平行线的方法把长方形画完整。
49.以点O为顶点,画一个136°的角。
50.分别用三角板和量角器两种方法画一个的角。
《四年级暑假新课预习提升练专项练习检测卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版》参考答案
1.见详解
【分析】(1)线段有两个端点,不能向两端延伸,据此连接AB,即可得到线段AB;
(2)射线只有一个端点,只能向一端无限延伸,不能量出长度,据此连接BC并向C点的一端延长,即可画出射线BC;
(3)直线没有端点,可以向两端无限延伸,不能量出长度,据此连接AC并向两端延长,即可画出直线AC。
【详解】作图如下:
2.见详解
【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可在图中描出各点,并依次连成封闭图形。根据平移的特征,把这个图形的各顶点分别向右平移4格,依次连接即可得到向右平移4格后的图形。图形的形状和大小不变,只是图形的位置发生了变化。
【详解】据分析作图如下:
3.(1)见详解;(2)见详解
【分析】(1)图中1格表示10米,书报亭在商场东面,即商场的右面,距离是50米,即距离5格,据此标出书报亭的位置;
(2)公园在书报亭的北面,且距离是60米,即从书报亭向上6格的位置,即为公园的位置。
【详解】
(1)(2)
4.见详解
【分析】观察数轴,每个单位长度表示100万,100万100万地数,从9000万数4个百万是94000000,从9000万数10个百万是1亿,从1亿数5个百万是105000000。
【详解】
【点睛】此题考查的是大数在数轴上的表示。
5.见详解
【分析】画角:画一条射线用量角器的中心和射线的端点重合,0刻度线和射线重合,从射线端的0刻度线开始,数到要画的度数,在度数的刻度处点上一个小圆点。从射线的端点起,过刚才画好的小圆点画一条射线。最后再标注上角的符号和度数。
锐角度数大于0度小于90度;直角度数等于90度;钝角度数大于90度小于180度。
【详解】
【点睛】明确角的分类及角的画法是解决本题关键。
6.具体画法见详解
【分析】使量角器的中心与给出的射线的端点重合,0刻度线与给出的射线重合。再在量角器上对准要画角的度数的刻度线,并点上一点。然后以已画出的射线的端点为端点,通过刚画的点,再画一条射线,这两条射线所成的夹角就是所要画的角度。据此画一个125°的角。
【详解】具体画法如图所示:
7.见详解
【分析】由题目可知,根据利用方向和距离确定物体位置的方法,先确定方向,再确定距离。通过观察图形可知,图中每格表示10米,从花园小区往西数3格就是超市的位置,从花园小区往东数7格就是中学的位置,从超市往南数2格就是中心广场,据此作图即可。
【详解】如图:
8.见详解
【分析】把直角三角尺的一条直角边与OB重合,使得点P在直角三角尺的另一条直角边上,将直尺紧靠这条直角边,沿着直尺的边过点P画直线即为OB的平行线;把直角三角尺的一条直角边与OA重合,使得点P在直角三角尺的另一条直角边上,沿着直角三角尺的这条直角边过点P向OA作直线即为OA边的垂线。
【详解】
【点睛】考查学生借助直角三角尺以及直尺作已知直线的平行线与垂线的方法。
9.见详解
【分析】图中方向已给出,可知一格代表10米, 30米即为3格,50米即为5格,20米即为2格,据此画图即可。
【详解】
10.见详解
【分析】射线只有一个端点,因此以点A为端点过C点画一条直的线,即可得到射线AC;
使量角器的中心和射线的A点重合,0°刻度线和射线AC重合,然后在量角器80°刻度线的地方点一个点,最后以画出的射线的端点为端点,通过刚画的点,再画一条射线;依此画图并标上对应的度数即可。
【详解】画图如下:
【点睛】解答此题的关键是要熟练掌握射线的特点,以及应掌握用量角器画角的方法。
11.见详解
【分析】直线外一点到直线上各点的连线中,垂线段最短,从饲养场作小河的垂线段,沿垂线段挖可以使水渠最短。
【详解】
【点睛】本题主要考查学生对垂线的特征及性质的掌握和灵活运用。
12.见详解
【分析】(1)根据直线没有端点,无限延长,画直线AB。
(2)根据射线只有一个端点,无限延长,画射线AD。
(3)把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和C点重合,过C点沿三角板的直角边,向已知直线画直线即可。
(4)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和D点重合,过D点沿三角板的直角边画直线即可。
【详解】(1)(2)(3)(4)如图:
13.见详解
【分析】用计数器表示数字时,哪个数位上是几,就在那个数位上拨几个珠子。
34000,这个数的千位是4,拨4个珠子,万位是3,拨3个珠子,个位、十位和百位是0,不拨珠子;
160500,这个数的百位是5,拨5个珠子,万位是6,拨6个珠子,十万位是1,拨1个珠子,个位、十位和千位是0,不拨珠子。
【详解】
14.见详解
【分析】过直线上或直线外一点作垂线的步骤:
①把三角尺的一条直角边与已知直线重合;
②沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上;
③沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是已知直线的垂线。
【详解】作图如下:
15.见详解
【分析】(1)过直线外一点作直线的平行线:把三角板的一边靠紧直线,另一边靠紧一直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线就是过该点作的直线的平行线;过A点作国道的平行线即可。
(2)直线外一点到直线上各点的连线中,垂线段最短,从幸福村作国道的垂线段,沿垂线段修村道最近。
【详解】(1)(2)见下图:
【点睛】熟练掌握平行线和垂线的画法是解答本题的关键。
16.见详解
【分析】从直线外一点到这条直线所画的所有线段中,垂线段最短。所以在垂线段与直线的交点处设地铁口,才能使在该写字楼工作的人到地铁口最近。
分别过点P向道路A和道路B作垂线,并标出垂足点。经测量发现,点P与B道路的距离更近,所以地铁口应设在点C。
【详解】根据分析画图如下:
经测量发现,点P与B道路的距离更近,所以地铁口应设在点C。
17.见详解
【分析】可能性的大小与区域的大小有关,某种颜色所占的区域大则停在该区域的可能性就大,反之就小;由题意可知,转盘内有黄、红、蓝三种颜色且蓝字的区域最小,黄字区域最大。共有8个区域,则黄字区域有5个,红字区域有2个,蓝字区域有1个,据此作图即可。
【详解】如图所示:
(答案不唯一)
【点睛】本题考查可能性,明确可能性的大小与区域的大小有关是解题的关键。
18.(1)图见详解
(2)∠O > ∠A
(3)图见详解;平行
【分析】(1)画角的步骤是:使量角器的中心和O点重合,0°刻度线和已知射线重合,然后在量角器65°刻度线的地方点一个点,最后以画出的射线的端点为端点,通过刚画的点,再画一条射线;
(2)用量角器测量出∠A的度数,再比较;用量角器测量角时,量角器的中心和角的顶点重合,0刻度线和角的一边重合,另一边所指的刻度就是角的大小;
(3)从线段外一点到这条线段所画的垂直线段最短,它的长度叫作点到线段的距离;把直角三角尺的一边与线段AB重合,使得D点在另一条直角边上,过点D沿着另一条直角边画线段交AB与E点,即DE为点D到AB的距离(标上垂直符号),也就是到线AB距离最近的线段。两条直线都与第三条直线垂直,那么这两条直线也互相平行,据此解答。
【详解】(1)65°角如下图:
(2)根据分析可测量出∠A=58°,65°>58°,也就是∠O > ∠A;
(3)根据分析可画出到线AB距离最近的线段DE,如下图:
根据题意可知,线段DE和线段BC都与线段AB垂直,所以DE∥AB,也就是这条线段与线段BC的位置关系是平行。
19.见详解
【分析】省略万后面的尾数要看千位上的数,根据四舍五入法的原则,若千位上的数字大于等于5,就向万位进1;若千位上的数字小于5,就舍去千位及其后面数位上的数。据此解答即可。
【详解】“四舍”得到的10万最大,是104999;“五入”得到的10万最小,是95000。
20.见详解
【分析】直线外一点与直线上各点的连线中,垂线段最短,分别从两个村作公路的垂线段,沿垂线段修最短。
【详解】
【点睛】本题主要考查学生对垂直的特征及性质的掌握和灵活运用。
21.①120;钝
②见详解
【分析】①角的测量方法:用量角器量角时,先把量角器的中心点与角的顶点重合, 0°刻度线与角的一条边重合。角的另一条边所对的量角器上的刻度,就是这个角的度数;大于90°且小于180°的角是钝角;
②用三角板的一条直角边和已知线段BC重合,沿重合的线段平移三角板,使三角板的另一条直角边和P点重合,过P沿直角边向已知线段画垂线即可。
【详解】①通过测量可知,∠ABC=120°,120°<180°,则它是一个钝角。
②如下图:
22.见详解
【分析】过一点作直线的垂线:把三角板的一直角边靠紧直线,沿这条直线滑动三角板,当另一直角边经过该点时,沿这条直角边画的直线就是过该点作的直线的垂线;
过直线外一点作直线的平行线:把三角板的一边靠紧直线,另一边靠紧一直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线就是过该点作的直线的平行线。
【详解】
【点睛】熟练掌握垂线和平行线的画法是解答本题的关键。
23.见详解
【分析】从直线外一点到这条直线所画的垂直线段最短,它的长度叫作点到直线的距离;因此过A点作河边的垂线段即可。
过一点作已知直线的垂线:把三角板的一直角边靠紧直线,沿这条直线滑动三角板,当另一直角边经过该点时,沿这条直角边画的直线就是过该点作的直线的垂线,依此画图并标上垂直符号即可。
【详解】画图如下:
24.见详解
【分析】使量角器的中心和射线的端点重合,零刻度线和射线重合,在量角器上140度刻度线的地方点一个点,然后以射线的端点为端点,通过刚画的点,再画一条射线,这两条射线所夹的角就是140°的角。
【详解】
25.(1)第②条路最近; 因为两点之间线段最短。
(2)王大爷去河边挑水应走垂直线;见详解
【分析】(1)首先明确两点之间线段最短,王大爷去集市走第②条路最近。
(2)直线外一点到直线的线段中, 垂线段最短, 所以王大爷去河边挑水应走垂直线。从王大爷家向河边画垂线即可。
【详解】根据分析可知:
(1)王大爷去集市走第②条路最近, 因为两点之间线段最短。
(2)王大爷去河边挑水应走垂直线。画图如下:
26.(1)(2,4);(5,5);(7,2)
(2)见详解。
【分析】根据图示,结合所学知识,确定位置,先列后行,数对中第一个数表示在第几列,第二个数表示在第几行,根据这个,可以得出鸟林的位置、熊猫馆的位置和老虎馆的位置该如何表示。
【详解】(1)依题意,结合所学知识,鸟林在第二列,第四行,其位置用数对表示为(2,4),熊猫馆在第五列,第五行,其位置用数对表示为(5,5),老虎馆在第七列,第二行,其位置用数对表示为(7,2)。
(2)大象馆的位置用数对表示为(3,2),意味着其在第3列,第2行,对应位置如下图;同理可得猎豹馆的位置。如下图表示:
【点睛】本题考查学生对用数对表示位置知识的理解和掌握,学生能够熟记规则是解答的关键。
27.见详解
【分析】画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合。在量角器70°刻度线的地方点一个点。以画出的射线的端点为端点,通过刚画的点,再画一条射线。据此画出70°的角。同理画出38°和135°的角。
【详解】
28.见详解。
【分析】从家去学校,可以看成两点之间,找最短的距离,根据两点之间线段最短可以画出。从家尽快到河边,可以看成是直线外一点到之间的距离,根据垂线段最短知识可以画出。
【详解】依题意,结合所学知识,两点间线段最短,直接画线段连接小安家和学校;根据垂线段最短,可以得出从小安家画一条垂线与河边垂直即可。如下图所示:
【点睛】本题考查两点之间线段最短和垂线段最短知识,学生熟练掌握是解题的关键。
29.见详解
【分析】根据同一平面内,永不相交的两条直线叫做平行线,平行线之间的距离处处相等,先画一条线段,利用平移即可作出它的平行线,据此画图即可。
【详解】据分析作图如下:
(答案不唯一)
30.见详解
【分析】角的度量方法:用量角器量角时,先把量角器的中心与角的顶点重合, 0°刻度线与角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数;如果角的起始边不是与0刻度线重合,角的度数为两条边所对的刻度之差。
【详解】
【点睛】本题主要考查学生用量角器度量角度数方法的掌握和灵活运用。
31.(1)见详解
(2)见详解
【分析】(1)根据两点之间线段最短,将实验室与教学楼用直尺进行连线即可得到教学楼到实验室最近的路;
(2)点到直线之间,垂线段最短,因此,过教学楼一点向操场的一边作垂线与操场一边相交的点即为垂足,教学楼与垂足之间的距离即为教学楼到操场最近的路。
【详解】(1)教学楼到实验室最近的路如下图:
(2)教学楼到操场最近的路如下图:
32.见详解
【分析】用三角板的一条直角边和已知直线重合,用直尺紧靠三角板的另一条直角边,按住直尺不动,沿直尺平移三角板一段距离后,沿着这条直角边画一条直线,所画直线与已知直线平行,据此作图即可。
【详解】画一条直线与已知直线平行,如下图所示:
(答案不唯一)
【点睛】经过直线外一点有且只有一条直线与已知直线平行;因为直线外有无数点,所以有无数条直线与已知直线平行。
33.标数见详解
【分析】从图上可以看出,800万和900万之间相差100万,平均分成了10份,每份是10万;950万比900万多50万,也就是多5个10万,即在900万右边第5格处;1000万比900万多100万,也就是多10个10万,即在900万右边第10格处;895万可以看作800万加90万再加5万,先在800万右边第9格处找到890万,5万是10万的一半,即895万在890万和900万中间处;据此解答。
【详解】根据分析,标数如下:
34.见详解
【分析】把三角尺的一条直角边与已知直线重合,使得点A在三角尺的另一条直角边上,把直尺与三角尺的这条直角边重合,沿着直尺过点A画直线即为已知直线的平行线。
【详解】
【点睛】画图时借助直尺和三角尺画平行线。在同一平面内,永不相交的两条直线互相平行。
35.见详解
【分析】(1)用三角板的一条直角边的已知直线AB重合,沿重合的直线AB平移三角板,使三角板的另一条直角边和O点重合,过O点沿直角边向已知直线AB画直线即可;
(2)把三角板的一条直角边与已知直线AB重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线AB重合的直角边和O点重合,过O点沿三角板的直角边画直线即可。
【详解】据分析作图如下:
【点睛】本题主要考查了平行线和垂线的作法,培养学生的作图能力。
36.见详解
【分析】用直角三角尺的一条直角边和直线重合,移动三角尺,使三角尺的另一条直角边和点A重合,过A点沿直角边向已知直线画直线即是过A点作出的直线的垂线。把三角尺的一条直角边和已知直线重合,用直尺靠紧三角尺的另一条直角边,沿直尺移动三角尺,使三角尺原来和已知直线重合的直角边和A点重合,过A点沿三角尺的直角边画直线即是过A点作出的直线的平行线。
【详解】
【点睛】此题考查了学生用三角尺和直尺作垂线和平行线的能力。
37.见详解
【分析】把三角板的一条直角边与已知直线CD重合,沿直线移动三角板,使三角板的另一条直角边和O点重合,过O点沿三角板的直角边,向已知直线CD画直线即为其垂线。
把三角板的一条直角边与已知直线AB重合,把直尺靠紧三角板的另一条直角边,使得点O在另一条直角边上,移动直尺,沿着直尺过点O画直线即为所求平行线。
【详解】作图如下:
【点睛】本题考查了学生平行线和垂线的作法,培养学生的作图能力。
38.图见详解
【分析】(1)长方形的特征:两组对边平行且相等,有4个直角;用三角尺的直角边分别紧靠长方形的长和宽,然后平移三角尺至长(宽)的另一端点处,在三角尺的另一条直角边上,过该端点画出与之长(宽)平行且相等的线段,依此画出长方形的另外两条边即可;
(2)在同一平面内,点到直线的所有连线中,垂线段最短;显然,点M离长方形的宽比较近,因此用三角尺的直角边与长方形的宽重合,另一直角边平移至点M处,沿着直角边即可画出垂线段(不出头),最后标上直角符号即可。
【详解】根据分析作图如下:
39.见详解
【分析】沿直尺的0刻度线到3厘米刻度线画出的图形就是3厘米长的线段,标上端点和长度;使量角器的中心点和线段的端点A重合,0刻度线和线段AB重合,在量角器上找到65°度数的地方点一个点,以点A为端点,通过刚画的点,再画一条射线,组成的图形就是65°的角,在角内标上角的符号和度数;用直角三角尺的一条直角边和线段AB重合,沿另一直角边向线段AB画直线即可。
【详解】
【点睛】此题考查了学生画线段和角以及画垂线的能力。
40.见详解
【分析】过直线外一点作直线的平行线:把三角板的一条直角边靠紧直线,另一条直角边靠紧直尺,沿直尺滑动三角板,当与直线重合的一边经过已知点时,沿这边画直线就是过该点作的直线的平行线。
【详解】画图如下:
41.见详解
【分析】画角的步骤:先画一条射线,使量角器的中心和射线的端点重合,零刻度线和射线重合,在量角器上要画的角的度数刻度线的地方点一个点,然后以画出的射线的端点为端点,通过刚刚画的点,再画一条射线,这两条射线所夹的角就是我们所要画的角。
【详解】如图:
【点睛】熟练掌握用量角器画角的方法是解答本题的关键。
42.见详解
【分析】(1)过直线上或直线外一点作垂线的方法:先把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号。这条直线就是已知直线的垂线。
(2)过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。固定直尺,然后沿着直尺平移三角尺,使直线外的点在三角尺上。沿直角边画出另一条直线即可。
【详解】
43.见详解
【分析】因为直线外一点与这条直线所有点的连线中,垂线段最短,所以,只要作出小羊到小河的垂线段即可。
【详解】根据垂直线段最短的性质,即可画出这条从小羊到河边最近的线路,如图所示:
【点睛】此题考查了垂直线段最短的性质的在解决实际问题中的灵活应用。
44.见详解
【分析】先画一条射线使量角器的中心和射线的端点重合,零刻度线和射线重合,在量角器所画角度刻度线的地方点一个点,以射线的端点为端点,通过刚画的点,再画一条射线即可。
【详解】
【点睛】本题考查了学生根据所给度数利用作图工具画角的动手能力。
45.见详解
【分析】用直角三角尺的一条直角边和直线重合,沿直角三角尺的另一条直角边向已知直线画直线即可。
【详解】
【点睛】此题考查了学生用三角尺作垂线的能力。
46.见详解
【分析】将量角器的中心对准O,然后将量角器的0刻度线与角的一边重合,由于O在左边,所以角的开口向右,此时观察量角器的外圈刻度,找到120°处标一点,然后连接这个点与点O即可得到一个120°的角。
【详解】
47.见详解
【分析】先确定一个端点,引出一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合;再在量角器上对准要画角的度数的刻度线,并点上一个点;然后以已画出的射线的端点为端点,通过刚画的点,再画一条射线,这两条射线所成的夹角就是所要画的角度。
【详解】
【点睛】本题主要考查学生对用量角器画角方法的掌握。
48.见详解
【分析】长方形的特征:长方形两组对边平行且相等,两条对角线相等且互相平分,长方形是特殊的平行四边形;
过直线外一点画平行线:固定三角尺,沿一条直角边先画一条直线;用直尺紧靠着三角尺的另一条直角边,固定直尺,然后沿着直尺平移三角尺;平移后,沿直角边画出另一条直线;
过直线上或直线外一点作垂线的步骤:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使直线上或直线外的点在三角尺的另一条直角边上;沿三角尺的另一条直角边画一条直线,并画上垂直符号;这条直线就是已知直线的垂线;据此作图。
【详解】如图:
【点睛】掌握长方形的特征,以及垂线和平行线的画法是解答本题的关键。
49.见详解
【分析】以O点为端点画一条射线,使量角器的中心点和点O重合,0刻度线和射线重合,在量角器上找到136°度数的地方点一个点,以点O为端点,通过刚画的点,再画一条射线,组成的图形就是136°的角,在角内标上角的符号和度数。
【详解】
【点睛】画角的方法可以总结为一画射线,二重合,三找点,四连线,五标度数,六检查。
50.见详解
【分析】(1)画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合,在量角器150°刻度线的地方点一个点,以画出的射线的端点为端点,通过刚画的点,再画一条射线,据此画出150°的角。
(2)用三角尺上的90°的角,画一个角,再在这个画的90°角的外部,用三角尺上的60°的角同90°的角在顶点重合,一条边重合,画出60°的角,这两个角拼成的角就是150°的角,据此解答。
【详解】根据分析,用量角器画角如下:
三角尺画角如下:
【点睛】本题考查了量角器画角的方法和用三角尺上的角进行组合画角的方法,注意用量角器时,量角器的中心和射线的端点要重合。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
