2026中考数学专题复习 二次函数的实际应用三年真题汇总(含解析)
文档属性
| 名称 | 2026中考数学专题复习 二次函数的实际应用三年真题汇总(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:14:58 | ||
图片预览



文档简介
2026中考数学专题复习二次函数的实际应用三年真题汇总
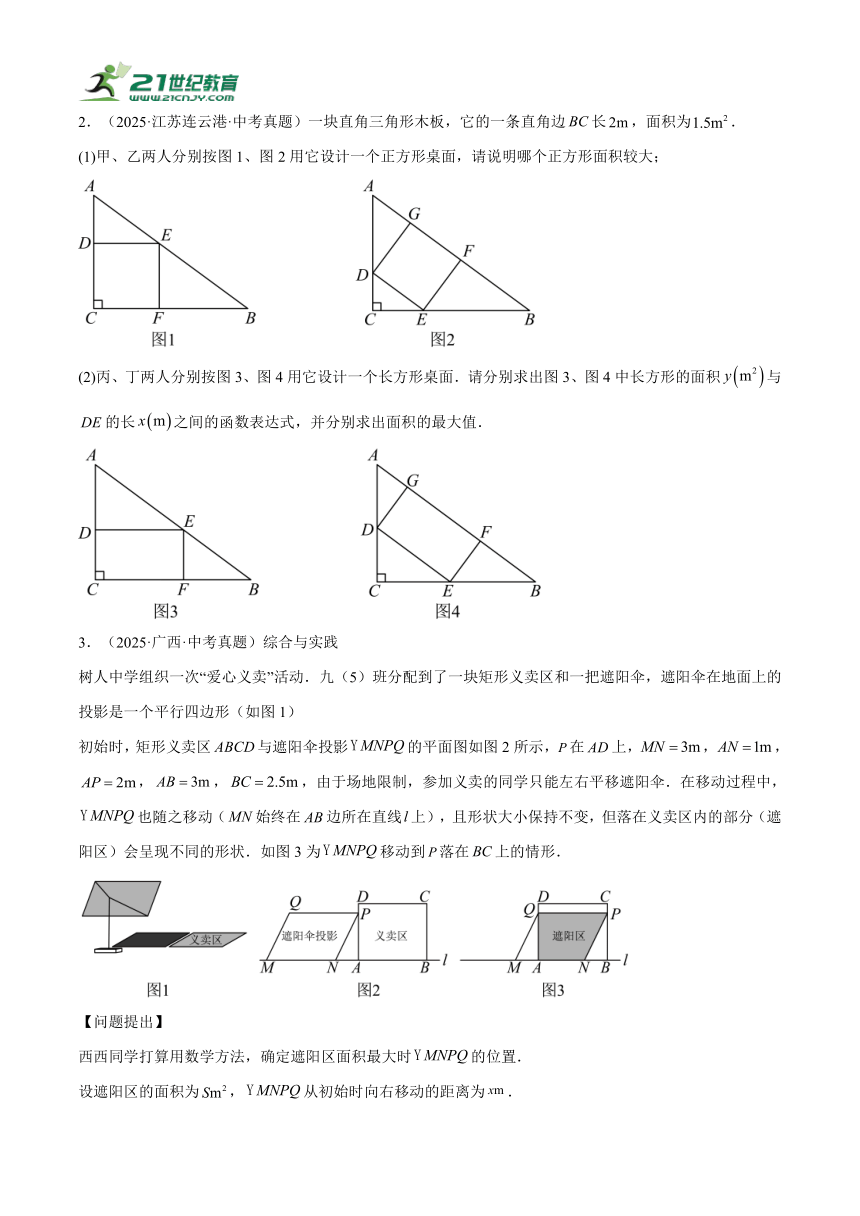
1.(2025·内蒙古·中考真题)问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为.在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴.建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
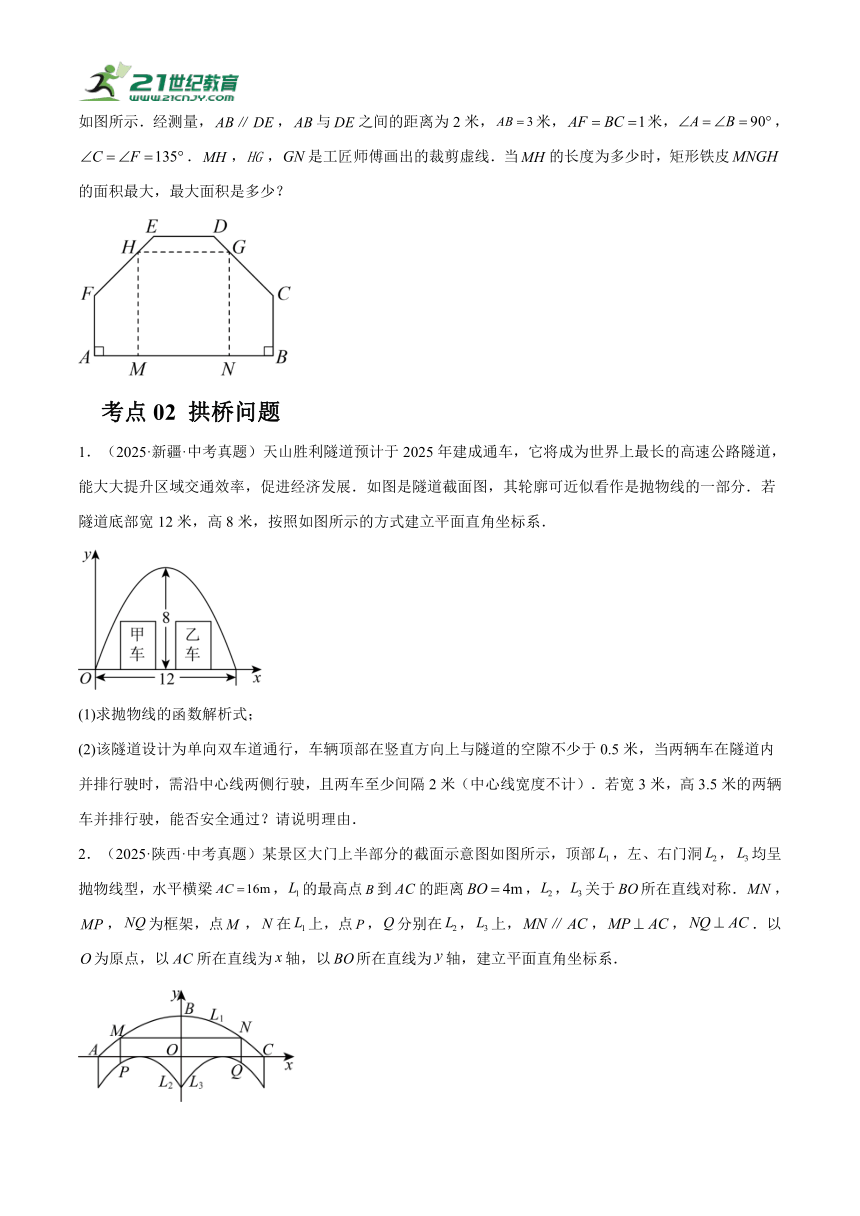
2.(2025·江苏连云港·中考真题)一块直角三角形木板,它的一条直角边长,面积为.
(1)甲、乙两人分别按图1、图2用它设计一个正方形桌面,请说明哪个正方形面积较大;
(2)丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积与的长之间的函数表达式,并分别求出面积的最大值.
3.(2025·广西·中考真题)综合与实践
树人中学组织一次“爱心义卖”活动.九(5)班分配到了一块矩形义卖区和一把遮阳伞,遮阳伞在地面上的投影是一个平行四边形(如图1)
初始时,矩形义卖区与遮阳伞投影的平面图如图2所示,在上,,,,,,由于场地限制,参加义卖的同学只能左右平移遮阳伞.在移动过程中,也随之移动(始终在边所在直线上),且形状大小保持不变,但落在义卖区内的部分(遮阳区)会呈现不同的形状.如图3为移动到落在上的情形.
【问题提出】
西西同学打算用数学方法,确定遮阳区面积最大时的位置.
设遮阳区的面积为,从初始时向右移动的距离为.
【直观感知】(1)从初始起右移至图3情形的过程中,随的增大如何变化?
【初步探究】(2)求图3情形的与的值;
【深入研究】(3)从图3情形起右移至与重合,求该过程中关于的解析式;
【问题解决】(4)当遮阳区面积最大时,向右移动了多少?(直接写出结果)
4.(2024·湖北·中考真题)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
5.(2024·山东潍坊·中考真题)【问题提出】
在绿化公园时,需要安装一定数量的自动喷洒装置,定时喷水养护,某公司准备在一块边长为的正方形草坪(如图1)中安装自动喷洒装置,为了既节约安装成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方案.
说明:一个自动喷洒装置的喷洒范围是半径为的圆面.喷洒覆盖率,为待喷洒区域面积,为待喷洒区域中的实际喷洒面积.
【数学建模】
这个问题可以转化为用圆面覆盖正方形面积的数学问题.
【探索发现】
(1)如图2,在该草坪中心位置设计安装1个喷洒半径为的自动喷洒装置,该方案的喷洒覆盖率______.
(2)如图3,在该草坪内设计安装4个喷洒半径均为的自动喷洒装置;如图4,设计安装9个喷洒半径均为3m的自动喷洒装置;,以此类推,如图5,设计安装个喷洒半径均为的自动喷洒装置.与(1)中的方案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒覆盖率?请判断并给出理由.
(3)如图6所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,且使得该草坪的喷洒覆盖率.已知正方形各边上依次取点F,G,H,E,使得,设,的面积为,求关于的函数表达式,并求当取得最小值时的值.
【问题解决】
(4)该公司现有喷洒半径为的自动喷洒装置若干个,至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率?(直接写出结果即可)
6.(2023·山东潍坊·中考真题)工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
考点02 拱桥问题
1.(2025·新疆·中考真题)天山胜利隧道预计于2025年建成通车,它将成为世界上最长的高速公路隧道,能大大提升区域交通效率,促进经济发展.如图是隧道截面图,其轮廓可近似看作是抛物线的一部分.若隧道底部宽12米,高8米,按照如图所示的方式建立平面直角坐标系.
(1)求抛物线的函数解析式;
(2)该隧道设计为单向双车道通行,车辆顶部在竖直方向上与隧道的空隙不少于0.5米,当两辆车在隧道内并排行驶时,需沿中心线两侧行驶,且两车至少间隔2米(中心线宽度不计).若宽3米,高3.5米的两辆车并排行驶,能否安全通过?请说明理由.
2.(2025·陕西·中考真题)某景区大门上半部分的截面示意图如图所示,顶部,左、右门洞,均呈抛物线型,水平横梁,的最高点到的距离,,关于所在直线对称.,,为框架,点,在上,点,分别在,上,,,.以为原点,以所在直线为轴,以所在直线为轴,建立平面直角坐标系.
(1)求抛物线的函数表达式;
(2)已知抛物线的函数表达式为,,求的长.
3.(2024·陕西·中考真题)一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
4.(2023·贵州·中考真题)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
考点03 销售问题
1.(2025·四川内江·中考真题)2025年春节期间,我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录,商家推出A、B两款“哪吒”文旅纪念品.已知购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元.
(1)求A、B两款“哪吒”纪念品每个进价分别为多少元?
(2)根据网上预约的情况,如果该商家计划用不超过12000元的资金购进A、B两款“哪吒”纪念品共400个,那么至少需要购进B款纪念品多少个?
(3)在销售中,该商家发现每个A款纪念品售价60元时,可售出200个,售价每增加1元,销售量将减少5个.设每个A款纪念品售价元,W表示该商家销售A款纪念品的利润(单位:元),求W关于a的函数表达式,并求出W的最大值.
2.(2025·四川南充·中考真题)学校计划租用客车送师生到某红色基地,参加主题为“缅怀先烈,强国有我”的研学活动,请阅读下列材料,并完成相关问题.
材料一 租车公司有A,B两种型号的客车可供租用,在每辆车满员情况下,每辆A型客车比每辆B型客车多载客15人;用A型客车载客600人与用B型客车载客450人的车辆数相同.
材料二 A型客车租车费用为3200元/辆;B型客车租车费用为3000元/辆. 优惠方案:租用A型客车m辆,租车费用元/辆; 租用B型客车,租车费用打八折.
材料三 租车公司最多提供8辆A型客车; 学校参加研学活动师生共有530人,租用A,B两种型号客车共10辆.
(1)A,B两种型号的客车每辆载客量分别是多少?
(2)本次研学活动学校的最少租车费用是多少?
3.(2024·山东青岛·中考真题)5月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季.为了解樱桃的收益情况,从第1天销售开始,小明对自己家的两处樱桃园连续15天的销售情况进行了统计与分析:
A樱桃园 第x天的单价、销售量与x的关系如下表: 单价(元/盒)销售量(盒)第1天5020第2天4830第3天4640第4天4450………第x天10x+10
第x天的单价与x近似地满足一次函数关系,已知每天的固定成本为745元. B樱桃园 第x天的利润(元)与x的关系可以近似地用二次函数刻画,其图象如图:
(1)A樱桃园第x天的单价是______元/盒(用含x的代数式表示);
(2)求A樱桃园第x天的利润(元)与x的函数关系式;(利润单价销售量固定成本)
(3)①与x的函数关系式是______;
②求第几天两处樱桃园的利润之和(即)最大,最大是多少元?
(4)这15天中,共有______天B樱桃园的利润比A樱桃园的利润大.
4.(2024·黑龙江大庆·中考真题)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的天中,第天且为整数)的售价为(元千克).当时,;当时,.销量(千克)与的函数关系式为,已知该产品第天的售价为元千克,第天的售价为元千克,设第天的销售额为(元).
(1) ,_____;
(2)写出第天的销售额与之间的函数关系式;
(3)求在试销售的天中,共有多少天销售额超过元?
5.(2024·贵州·中考真题)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
6.(2024·江苏盐城·中考真题)请根据以下素材,完成探究任务.
制定加工方案
生产背景 背景1 ◆某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式. ◆因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或“雅”服装1件,或“正”服装1件. ◆要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
背景2 每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为: ①“风”服装:24元/件; ②“正”服装:48元/件; ③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整理 现安排x名工人加工“雅”服装,y名工人加工“风”服装,列表如下: 服装种类加工人数(人)每人每天加工量(件)平均每件获利(元)风y224雅x1正148
探究任务 任务1 探寻变量关系 求x、y之间的数量关系.
任务2 建立数学模型 设该工厂每天的总利润为w元,求w关于x的函数表达式.
任务3 拟定加工方案 制定使每天总利润最大的加工方案.
7.(2023·湖北黄石·中考真题)某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元/件.设第个生产周期设备的售价为万元/件,售价与之间的函数解析式是,其中是正整数.当时,;当时,.
(1)求,的值;
(2)设第个生产周期生产并销售完设备的数量为件,且y与x满足关系式.
当时,工厂第几个生产周期获得的利润最大 最大的利润是多少万元
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.
考点04 投球问题
1.(2025·贵州·中考真题)用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点,运动路径近似为抛物线,且,石块在水面上弹起后第二次与水面接触于点,运动路径近似为抛物线,且.(小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
(1)如图②,当时,若点坐标为,求抛物线的表达式;
(2)在(1)的条件下,若,在水面上有一个截面宽,高的矩形的障碍物,点的坐标为,判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;
(3)小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中,求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)
2.(2025·江苏连云港·中考真题)如图,小亮同学掷铅球时,铅球沿抛物线运行,其中是铅球离初始位置的水平距离,是铅球离地面的高度.若铅球抛出时离地面的高度为,则铅球掷出的水平距离为 .
3.(2024·甘肃兰州·中考真题)在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:
水平距离 0 3 4 10 15 20 22 27
竖直高度 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据上表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.
4.(2024·青海·中考真题)在如图所示的平面直角坐标系中,有一斜坡,从点O处抛出一个小球,落到点处.小球在空中所经过的路线是抛物线的一部分.
(1)求抛物线的解析式;
(2)求抛物线最高点的坐标;
(3)斜坡上点B处有一棵树,点B是的三等分点,小球恰好越过树的顶端C,求这棵树的高度.
5.(2024·天津·中考真题)从地面竖直向上抛出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是.有下列结论:
①小球从抛出到落地需要;
②小球运动中的高度可以是;
③小球运动时的高度小于运动时的高度.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6.(2024·江西·中考真题)如图,一小球从斜坡O点以一定的方向弹出球的飞行路线可以用二次函数刻画,斜坡可以用一次函数刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如下表:
x 0 1 2 m 4 5 6 7 …
y 0 6 8 n …
(1)①______,______;
②小球的落点是A,求点A的坐标.
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系.
①小球飞行的最大高度为______米;
②求v的值.
7.(2023·浙江·中考真题)根据以下素材,探究完成任务.
如何把实心球掷得更远?
素材1
小林在练习投掷实心球,其示意图如图,第一次练习时,球从点A处被抛出,其路线是抛物线.点A距离地面,当球到OA的水平距离为时,达到最大高度为.
素材2
根据体育老师建议,第二次练习时,小林在正前方处(如图)架起距离地面高为的横线.球从点A处被抛出,恰好越过横线,测得投掷距离.
问题解决
任务1
计算投掷距离 建立合适的直角坐标系,求素材1中的投掷距离.
任务2
探求高度变化 求素材2和素材1中球的最大高度的变化量
任务3
提出训练建议 为了把球掷得更远,请给小林提出一条合理的训练建议.
8.(2023·内蒙古赤峰·中考真题)乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
水平距离x/
竖直高度y/
(1)在平面直角坐标系中,描出表格中各组数值所对应的点,并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是__________,当乒乓球落在对面球台上时,到起始点的水平距离是__________;
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274,球网高为15.25.现在已经计算出乒乓球恰好过网的击球高度的值约为1.27.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).
考点05 喷水问题
1.(2025·甘肃平凉·中考真题)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是,则水流喷出的最大高度是( )
A. B. C. D.
2.(2023·山东滨州·中考真题)如图,要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为3米,水柱落地处离池中心3米,水管长 米.
3.(2023·山东·中考真题)城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽.(结果精确到0.1米)参考数据:
4.(2023·吉林长春·中考真题)年5月8日,商业首航完成——中国民商业运营国产大飞机正式起步.时分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”、是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为米时,两条水柱在物线的顶点H处相遇,此时相遇点H距地面米,喷水口A、B距地面均为4米.若两辆消防车同时后退米,两条水柱的形状及喷水口、到地面的距离均保持不变,则此时两条水柱相遇点距地面 米.
答案解析
考点01 图形问题
1.(2025·内蒙古·中考真题)问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为.在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴.建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
【答案】(1),,
(2)抛物线和的顶点坐标分别为,, 的表达式为;的表达式为;
(3)
【分析】(1)由矩形性质可得,,,,即可得出坐标;
(2)由装置整体图案为轴对称图形,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,由矩形中,抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,即可得出抛物线和的顶点坐标分别为,,分别设抛物线和的表达式为,,分别将将和代入求解即可;
(3)由装置整体图案为轴对称图形,得出,,证明轴,设,则,,则,求得,由抛物线对称性可得.
【详解】(1)解:∵矩形的边,,
∴,,,,
∴,,;
(2)解:∵装置整体图案为轴对称图形,
如图,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,
结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,
∴四边形是矩形,
∴,
∵抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,
∴,,
∴抛物线和的顶点坐标分别为,,
分别设抛物线和的表达式为,,
将代入,
解得,
则抛物线的表达式为;
将代入,
解得;
则抛物线的表达式为;
(3)解:∵装置整体图案为轴对称图形,
∴,,
∵轴,
∴轴,
∵是矩形,
∴,
∴轴,
∴,
设,
∴,,
∴,
解得:或(在对称轴右侧,舍),
∴,
由抛物线对称性可得.
【点睛】本题考查二次函数的图象与几何综合,矩形的性质,平面直角坐标系,待定系数法求二次函数的解析式,二次函数的图象与性质,熟练掌握相关性质是解题的关键.
2.(2025·江苏连云港·中考真题)一块直角三角形木板,它的一条直角边长,面积为.
(1)甲、乙两人分别按图1、图2用它设计一个正方形桌面,请说明哪个正方形面积较大;
(2)丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积与的长之间的函数表达式,并分别求出面积的最大值.
【答案】(1)图1的正方形面积较大
(2)在图3中,,当时,长方形的面积有最大值为;在图4中,,当时,长方形的面积有最大值为
【分析】本题考查了相似三角形的判定与性质,勾股定理,正方形的性质,二次函数的应用,正确掌握相关性质内容是解题的关键.
(1)先运用勾股定理算出,再运用正方形的性质分别证明,,,然后代入数值化简得,进行计算得,然后进行比较,即可作答.
(2)与(1)同理证明,则长方形的面积,结合二次函数的图象性质得当时,长方形的面积有最大值为.,然后证明,,再把数值代入长方形的面积,化简得,结合二次函数的图象性质进行作答即可.
【详解】(1)解:∵,面积为,
∴,
∴.
设正方形的边长为,
∵四边形是正方形
∴,,
∵
∴
得,
即,
解得.
∵四边形是正方形
∴,
∴
∴,
得,
即,
∴.
,
∵
∴,
得,
即,
解得.
∵,
∴图1的正方形面积较大.
(2)解:∵四边形是长方形
∴,,
∵
∴;
得,
则,,
∴长方形的面积,
∵
∴开口向下,
当时,长方形的面积有最大值为.
在图4中,同理得,
得,
∴,,
同理得,
得,
则,
∴长方形的面积,
∵
∴开口向下,
∴当时,长方形的面积有最大值为.
3.(2025·广西·中考真题)综合与实践
树人中学组织一次“爱心义卖”活动.九(5)班分配到了一块矩形义卖区和一把遮阳伞,遮阳伞在地面上的投影是一个平行四边形(如图1)
初始时,矩形义卖区与遮阳伞投影的平面图如图2所示,在上,,,,,,由于场地限制,参加义卖的同学只能左右平移遮阳伞.在移动过程中,也随之移动(始终在边所在直线上),且形状大小保持不变,但落在义卖区内的部分(遮阳区)会呈现不同的形状.如图3为移动到落在上的情形.
【问题提出】
西西同学打算用数学方法,确定遮阳区面积最大时的位置.
设遮阳区的面积为,从初始时向右移动的距离为.
【直观感知】(1)从初始起右移至图3情形的过程中,随的增大如何变化?
【初步探究】(2)求图3情形的与的值;
【深入研究】(3)从图3情形起右移至与重合,求该过程中关于的解析式;
【问题解决】(4)当遮阳区面积最大时,向右移动了多少?(直接写出结果)
【答案】(1)随的增大而增大;(2),;(3);(4)
【分析】(1)根据矩形的性质得,根据平行四边形的面积公式得,然后分别求出当时,当时,关于的解析式,即可得出结论;
(2)根据(1)的结论可得答案;
(3)当时,如图,设向右移动后得到,设交于点,交于点,交于点,则,,
此时遮阳区的面积为六边形的面积,推出,,得,,再根据即可得出结论;
(4)分别确定:当时,当时,当时,各个范围内的最大值,即可得出结论.
【详解】解:(1)∵四边形是矩形,四边形是平行四边形,,,,在边所在直线上,
∴,,,
又∵如图2,在上,,,
∴,
,
当时,如图,设交于点,交于点,则,
此时遮阳区的面积为的面积,
∵,
∴,,
∴,
∴,
∴,
∴当时,随的增大而增大,的值从增大到;
当时,如图,设交于点,则,,,
此时遮阳区的面积为四边形的面积,
∵,
∴四边形为梯形,
∴,
∴当时,随的增大而增大,的值从增大到;
综上所述,从初始起右移至图3情形的过程中,随的增大而增大;
(2)如图3,此时点落在上,则,
由(1)知:当时,;
∴图3情形时,,;
(3)当时,如图,设向右移动后得到,设交于点,交于点,交于点,则,,
此时遮阳区的面积为六边形的面积,
∴,,,
∴,,
∴,,
∴,,
∴
,
∴从图3情形起右移至与重合,该过程中关于的解析式为;
(4)当时,,
当时,的最大值为:;
当时,,
当时,的最大值为:;
当时,,
∵
∴当时,的最大值为:,
综上所述,当时,取得最大值,最大值为,
∴当遮阳区面积最大时,向右移动了.
【点睛】本题考查平移的性质,矩形的性质,平行四边形的性质,锐角三角函数的定义,列函数关系式,二次函数的最值,等积变换等知识点,利用分类讨论的思想及数形结合的思想解决问题是解题的关键.
4.(2024·湖北·中考真题)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
【答案】(1),
(2)
(3)当时,实验田的面积S最大,最大面积是
【分析】本题考查了矩形的性质,二次函数的实际应用,计算的取值范围是解题的关键.
(1)根据,求出与的函数解析式,根据矩形面积公式求出与的函数解析式;
(2)先求出的取值范围,再将代入函数中,求出的值;
(3)将与的函数配成顶点式,求出的最大值.
【详解】(1)解:,
,
,
;
(2),
,
,
,
当时,,
,
,
,
当时,矩形实验田的面积能达到;
(3),
当时,有最大值.
5.(2024·山东潍坊·中考真题)【问题提出】
在绿化公园时,需要安装一定数量的自动喷洒装置,定时喷水养护,某公司准备在一块边长为的正方形草坪(如图1)中安装自动喷洒装置,为了既节约安装成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方案.
说明:一个自动喷洒装置的喷洒范围是半径为的圆面.喷洒覆盖率,为待喷洒区域面积,为待喷洒区域中的实际喷洒面积.
【数学建模】
这个问题可以转化为用圆面覆盖正方形面积的数学问题.
【探索发现】
(1)如图2,在该草坪中心位置设计安装1个喷洒半径为的自动喷洒装置,该方案的喷洒覆盖率______.
(2)如图3,在该草坪内设计安装4个喷洒半径均为的自动喷洒装置;如图4,设计安装9个喷洒半径均为3m的自动喷洒装置;,以此类推,如图5,设计安装个喷洒半径均为的自动喷洒装置.与(1)中的方案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒覆盖率?请判断并给出理由.
(3)如图6所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,且使得该草坪的喷洒覆盖率.已知正方形各边上依次取点F,G,H,E,使得,设,的面积为,求关于的函数表达式,并求当取得最小值时的值.
【问题解决】
(4)该公司现有喷洒半径为的自动喷洒装置若干个,至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率?(直接写出结果即可)
【答案】(1);(2)不能,理由见解析;(3);当取得最小值时;(4)
【分析】(1)根据定义,分别计算圆的面积与正方形的面积,即可求解;
(2)根据(1)的方法求得喷洒覆盖率即可求解;
(3)根据勾股定理求得的关系,进而根据圆的面积公式得出函数关系式,根据二次函数的性质,即可求解;
(4)根据(3)的结论可得当圆为正方形的外接圆时,面积最小,则求得半径为的圆的内接正方形的边长为,进而将草坪分为个正方形,即可求解.
【详解】(1)当喷洒半径为时,喷洒的圆面积.
正方形草坪的面积.
故喷洒覆盖率.
(2)对于任意的,喷洒面积,而草坪面积始终为.
因此,无论取何值,喷洒覆盖率始终为.
这说明增加装置个数同时减小喷洒半径,对提高喷洒覆盖率不起作用.
(3)如图所示,连接,
要使喷洒覆盖率,即要求,其中为草坪面积,为喷洒面积.
∴都经过正方形的中心点,
在中,,,
∵
∴,
在中,
∴
∴
∴当时,取得最小值,此时
解得:
(4)由(3)可得,当的面积最小时,此时圆为边长为的正方形的外接圆,
则当时,圆的内接正方形的边长为
而草坪的边长为,,即将草坪分为个正方形,将半径为的自动喷洒装置放置于9个正方形的中心,此时所用装置个数最少,
∴至少安装个这样的喷洒装置可使该草坪的喷洒覆盖率
【点睛】本题考查了正方形与圆综合问题,二次函数的应用;本题要求我们先理解和计算喷洒覆盖率,然后通过调整喷洒装置的数量和喷洒半径来分析喷洒覆盖率的变化,最后在一个特定的条件下找出喷洒面积和喷洒半径之间的函数关系.解决此类问题的关键在于将实际问题转化为数学问题,即如何将喷洒覆盖率的计算问题转化为面积计算和函数求解问题.同时,在解决具体问题时,需要灵活运用已知的数学知识,如圆的面积公式,正方形面积公式,以及函数解析式求解等.最后,还需要注意将数学计算结果还原为实际问题的解决方案.
6.(2023·山东潍坊·中考真题)工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
【答案】当的长度为米时,矩形铁皮的面积最大,最大面积是平方米
【分析】连接,分别交于点,交于点,先判断出四边形是矩形,从而可得,再判断出四边形和四边形都是矩形,从而可得米,,然后设矩形的面积为平方米,米,则米,米,利用矩形的面积公式可得关于的二次函数,最后利用二次函数的性质求解即可得.
【详解】解:如图,连接,分别交于点,交于点,
,
,
米,
四边形是平行四边形,
又,
四边形是矩形,
,,
,
,
四边形是矩形,
,
四边形和四边形都是矩形,
米,,
和都是等腰直角三角形,
,
,
设矩形的面积为平方米,米,则米,米,
米,
米,
,
又,与之间的距离为2米,米,
,
由二次函数的性质可知,当时,随的增大而增大;当时,随的增大而减小,
则当时,取得最大值,最大值为,
答:当的长度为米时,矩形铁皮的面积最大,最大面积是平方米.
【点睛】本题考查了二次函数的几何应用、矩形的判定与性质等知识点,熟练掌握二次函数的性质是解题关键.
考点02 拱桥问题
1.(2025·新疆·中考真题)天山胜利隧道预计于2025年建成通车,它将成为世界上最长的高速公路隧道,能大大提升区域交通效率,促进经济发展.如图是隧道截面图,其轮廓可近似看作是抛物线的一部分.若隧道底部宽12米,高8米,按照如图所示的方式建立平面直角坐标系.
(1)求抛物线的函数解析式;
(2)该隧道设计为单向双车道通行,车辆顶部在竖直方向上与隧道的空隙不少于0.5米,当两辆车在隧道内并排行驶时,需沿中心线两侧行驶,且两车至少间隔2米(中心线宽度不计).若宽3米,高3.5米的两辆车并排行驶,能否安全通过?请说明理由.
【答案】(1)
(2)能安全通过,见解析
【分析】本题考查了二次函数的实际应用,正确理解题意是解题的关键.
(1)先得到顶点坐标,然后设顶点式,再代入即可求解,继而得到函数解析式;
(2)先求出点坐标,然后求出点距离抛物线的距离,然后减去车辆的高度,得到的差值与比较即可.
【详解】(1)解:由题意得,顶点为,即,
设抛物线的解析式为:
代入点得,
解得:,
∴抛物线解析式为;
(2)解:能安全通过,理由如下:
如图,
由题意得:,
将代入,
则,
∵,
∴能安全通过.
2.(2025·陕西·中考真题)某景区大门上半部分的截面示意图如图所示,顶部,左、右门洞,均呈抛物线型,水平横梁,的最高点到的距离,,关于所在直线对称.,,为框架,点,在上,点,分别在,上,,,.以为原点,以所在直线为轴,以所在直线为轴,建立平面直角坐标系.
(1)求抛物线的函数表达式;
(2)已知抛物线的函数表达式为,,求的长.
【答案】(1)
(2)
【分析】本题考查了二次函数的图象性质,二次函数的解析式,因式分解法进行解方程,正确掌握相关性质内容是解题的关键.
(1)理解题意,先设抛物线的函数表达式为,结合二次函数的对称性得,再代入进行求解,即可作答.
(2)理解题意,得出,再结合抛物线,的函数表达式分别为,,代入,整理得,再解方程,可作答.
【详解】(1)解:∵,
∴抛物线的顶点坐标为,
设抛物线的函数表达式为,
∵,
∴结合二次函数的对称性得,
将代入,
得
则,
∴;
(2)解:由(1)得抛物线的函数表达式,
∵,,.,且抛物线的函数表达式为,
∴,
整理得,
∴,
∴,
解得,
∴.
3.(2024·陕西·中考真题)一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
【答案】(1);
(2)的长为.
【分析】本题考查了二次函数的应用,待定系数法求二次函数解析式,根据题意求得函数解析式是解题的关键.
(1)根据题意设缆索所在抛物线的函数表达式为,把代入求解即可;
(2)根据轴对称的性质得到缆索所在抛物线的函数表达式为,由,把代入求得,,据此求解即可.
【详解】(1)解:由题意得顶点P的坐标为,点A的坐标为,
设缆索所在抛物线的函数表达式为,
把代入得,
解得,
∴缆索所在抛物线的函数表达式为;
(2)解:∵缆索所在抛物线与缆索所在抛物线关于y轴对称,
∴缆索所在抛物线的函数表达式为,
∵,
∴把代入得,,
解得,,
∴或,
∵,
∴的长为.
4.(2023·贵州·中考真题)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
【答案】(1)
(2)点的坐标为
(3)
【分析】(1)设抛物线的解析式为,将,代入即可求解;
(2)点B关于y轴的对称点,则,求出直线与y轴的交点坐标即可;
(3)分和两种情况,根据最小值大于等于9列不等式,即可求解.
【详解】(1)解:抛物线的对称轴与y轴重合,
设抛物线的解析式为,
,,
,,
将,代入,得:
,
解得,
抛物线的解析式为;
(2)解: 抛物线的解析式为,点到对称轴的距离是1,
当时,,
,
作点B关于y轴的对称点,
则,,
,
当,,A共线时,拉杆长度之和最短,
设直线的解析式为,
将,代入,得,
解得,
直线的解析式为,
当时,,
点的坐标为,位置如下图所示:
(3)解:中,
抛物线开口向下,
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
综上可知,或,
的取值范围为.
【点睛】本题考查二次函数的实际应用,涉及求二次函数解析式,求一次函数解析式,根据对称性求线段的最值,抛物线的增减性等知识点,解题的关键是熟练掌握二次函数的图象和性质,第3问注意分情况讨论.
考点03 销售问题
1.(2025·四川内江·中考真题)2025年春节期间,我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录,商家推出A、B两款“哪吒”文旅纪念品.已知购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元.
(1)求A、B两款“哪吒”纪念品每个进价分别为多少元?
(2)根据网上预约的情况,如果该商家计划用不超过12000元的资金购进A、B两款“哪吒”纪念品共400个,那么至少需要购进B款纪念品多少个?
(3)在销售中,该商家发现每个A款纪念品售价60元时,可售出200个,售价每增加1元,销售量将减少5个.设每个A款纪念品售价元,W表示该商家销售A款纪念品的利润(单位:元),求W关于a的函数表达式,并求出W的最大值.
【答案】(1)A款“哪吒”纪念品每个进价为40元,B款“哪吒”纪念品每个进价为20元;
(2)至少需要购进B款纪念品200个
(3),W的最大值为4500
【分析】本题主要考查了二元一次方程组的实际应用,二次函数的实际应用,一元一次不等式的实际应用,正确理解题意列出方程组,函数关系式和不等式是解题的关键.
(1)设A款“哪吒”纪念品每个进价为x元,B款“哪吒”纪念品每个进价为y元,根据购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元建立方程组求解即可;
(2)设需要购进B款纪念品m个,则需要购进A款纪念品个,根据购买资金不超过12000元建立不等式求解即可;
(3)根据题意可得每个A款纪念品的利润为元,销售量为个,据此列出W关于a的二次函数关系式,再利用二次函数的性质求出W的最大值即可.
【详解】(1)解:设A款“哪吒”纪念品每个进价为x元,B款“哪吒”纪念品每个进价为y元,
由题意得,,
解得,
答:A款“哪吒”纪念品每个进价为40元,B款“哪吒”纪念品每个进价为20元;
(2)解:设需要购进B款纪念品m个,则需要购进A款纪念品个,
由题意得,,
解得,
∴m的最小值为200,
答:至少需要购进B款纪念品200个;
(3)解:由题意得,
,
∵,
∴当,即时,W最大,最大值为4500.
2.(2025·四川南充·中考真题)学校计划租用客车送师生到某红色基地,参加主题为“缅怀先烈,强国有我”的研学活动,请阅读下列材料,并完成相关问题.
材料一 租车公司有A,B两种型号的客车可供租用,在每辆车满员情况下,每辆A型客车比每辆B型客车多载客15人;用A型客车载客600人与用B型客车载客450人的车辆数相同.
材料二 A型客车租车费用为3200元/辆;B型客车租车费用为3000元/辆. 优惠方案:租用A型客车m辆,租车费用元/辆; 租用B型客车,租车费用打八折.
材料三 租车公司最多提供8辆A型客车; 学校参加研学活动师生共有530人,租用A,B两种型号客车共10辆.
(1)A,B两种型号的客车每辆载客量分别是多少?
(2)本次研学活动学校的最少租车费用是多少?
【答案】(1)A型客车每辆载客量为60人,B型客车每辆载客量为45人
(2)本次研学活动学校最少租车费用为27 000元
【分析】本题主要考查了分式方程的应用,二次函数的实际应用,根据题意得到等量关系式是解题的关键.
(1)设A型客车每辆载客量为人,根据题意列出方程,求解即可;
(2)设租A型客车辆,B型客车辆,租车总费用,根据材料三先求出m的取值范围,再列出w关于m的函数关系式,结合二次函数的性质解答即可.
【详解】(1)解:设A型客车每辆载客量为人,根据题意得:
.
解之得.
经检验:是方程的根,且符合题意,
答:A型客车每辆载客量为60人,B型客车每辆载客量为45人.
(2)解:设租A型客车辆,B型客车辆,租车总费用,则
.
解之得.
.
∵,且对称轴为,
∴时,随着的增大而增大.
∵取正整数,且,
∴当时,最小值为27000(元).
∴本次研学活动学校最少租车费用为27000元
3.(2024·山东青岛·中考真题)5月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季.为了解樱桃的收益情况,从第1天销售开始,小明对自己家的两处樱桃园连续15天的销售情况进行了统计与分析:
A樱桃园 第x天的单价、销售量与x的关系如下表: 单价(元/盒)销售量(盒)第1天5020第2天4830第3天4640第4天4450………第x天10x+10
第x天的单价与x近似地满足一次函数关系,已知每天的固定成本为745元. B樱桃园 第x天的利润(元)与x的关系可以近似地用二次函数刻画,其图象如图:
(1)A樱桃园第x天的单价是______元/盒(用含x的代数式表示);
(2)求A樱桃园第x天的利润(元)与x的函数关系式;(利润单价销售量固定成本)
(3)①与x的函数关系式是______;
②求第几天两处樱桃园的利润之和(即)最大,最大是多少元?
(4)这15天中,共有______天B樱桃园的利润比A樱桃园的利润大.
【答案】(1)
(2)
(3)①;②第10天两处樱桃园的利润之和(即)最大,最大是4800元;
(4)4
【分析】本题主要考查了二次函数的实际应用,一次函数的实际应用:
(1)设出对应的函数解析式,利用待定系数法求解即可;
(2)根据(1)所求结合利润单价销售量固定成本进行求解即可;
(3)①利用待定系数法求解即可;②根据前面所求求出的结果,再利用二次函数的性质求解即可;
(4)根据题意建立不等式,求出不等式的正整数解即可得到答案.
【详解】(1)解:第天的单价与满足的一次函数关系式为,
把代入中得,
∴,
∴第天的单价与满足的一次函数关系式为,
∴A樱桃园第x天的单价是元/盒,
故答案为:;
(2)解:由题意得,
(3)解:①把代入中得:,
解得,
∴;
②∵,,
∴
,
∵,且(x为正整数),
∴当时,有最大值,最大值为4800,
∴第10天两处樱桃园的利润之和(即)最大,最大是4800元;
(4)解:当时,则,
∴,
∴,
∴,
∵x的正整数解有4个,
∴这15天中,共有4天B樱桃园的利润比A樱桃园的利润大.
4.(2024·黑龙江大庆·中考真题)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的天中,第天且为整数)的售价为(元千克).当时,;当时,.销量(千克)与的函数关系式为,已知该产品第天的售价为元千克,第天的售价为元千克,设第天的销售额为(元).
(1) ,_____;
(2)写出第天的销售额与之间的函数关系式;
(3)求在试销售的天中,共有多少天销售额超过元?
【答案】(1),
(2)
(3)在试销售的天中,共有天销售额超过元
【分析】本题考查了一次函数与二次函数的综合应用;
(1)待定系数法求解析式,即可求解;
(2)根据销售额等于销量乘以售价,分段列出函数关系式,即可求解;
(3)根据题意,根据,列出方程,解方程,即可求解.
【详解】(1)解:依题意,将,代入,
∴
解得:
∴
故答案为:,.
(2)解:依题意,
当时,
当时,
∴
(3)解:依题意,当时,
当时,
解得:
为正整数,
∴第天至第天,销售额超过元
(天)
答:在试销售的天中,共有天销售额超过元
5.(2024·贵州·中考真题)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
【答案】(1)
(2)糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元
(3)2
【分析】本题考查了二次函数的应用,解题的关键是:
(1)利用待定系数法求解即可;
(2)设日销售利润为w元,根据利润=单件利润×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可;
(3)设日销售利润为w元,根据利润=单件利润×销售量-m×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可.
【详解】(1)解∶设y与x的函数表达式为,
把,;,代入,得,
解得,
∴y与x的函数表达式为;
(2)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为450,
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元;
(3)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为,
∵糖果日销售获得的最大利润为392元,
∴,
化简得
解得,
当时,,
则每盒的利润为:,舍去,
∴m的值为2.
6.(2024·江苏盐城·中考真题)请根据以下素材,完成探究任务.
制定加工方案
生产背景 背景1 ◆某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式. ◆因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或“雅”服装1件,或“正”服装1件. ◆要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
背景2 每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为: ①“风”服装:24元/件; ②“正”服装:48元/件; ③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整理 现安排x名工人加工“雅”服装,y名工人加工“风”服装,列表如下: 服装种类加工人数(人)每人每天加工量(件)平均每件获利(元)风y224雅x1正148
探究任务 任务1 探寻变量关系 求x、y之间的数量关系.
任务2 建立数学模型 设该工厂每天的总利润为w元,求w关于x的函数表达式.
任务3 拟定加工方案 制定使每天总利润最大的加工方案.
【答案】任务1:;任务2:;任务3:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”服装,即可获得最大利润
【分析】题目主要考查一次函数及二次函数的应用,理解题意,根据二次函数的性质求解是解题关键.
任务1:根据题意安排x名工人加工“雅”服装,y名工人加工“风”服装,得出加工“正”服装的有人,然后利用“正”服装总件数和“风”服装相等,得出关系式即可得出结果;
任务2:根据题意得:“雅”服装每天获利为:,然后将2种服装的获利求和即可得出结果;
任务3:根据任务2结果化为顶点式,然后结合题意,求解即可.
【详解】解:任务1:根据题意安排70名工人加工一批夏季服装,
∵安排x名工人加工“雅”服装,y名工人加工“风”服装,
∴加工“正”服装的有人,
∵“正”服装总件数和“风”服装相等,
∴,
整理得:;
任务2:根据题意得:“雅”服装每天获利为:,
∴,
整理得:
∴
任务3:由任务2得,
∴当时,获得最大利润,
,
∴,
∵开口向下,
∴取或,
当时,,不符合题意;
当时,,符合题意;
∴,
综上:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”服装,即可获得最大利润.
7.(2023·湖北黄石·中考真题)某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元/件.设第个生产周期设备的售价为万元/件,售价与之间的函数解析式是,其中是正整数.当时,;当时,.
(1)求,的值;
(2)设第个生产周期生产并销售完设备的数量为件,且y与x满足关系式.
当时,工厂第几个生产周期获得的利润最大 最大的利润是多少万元
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.
【答案】(1),;
(2),;.
【分析】()用待定系数法求出,的值即可;
()当,根据利润(售价成本)设备的数量,可得出关于的二次函数,由函数的性质求出最值;
当时,关于的函数解析式,再画出关于的函数图象的简图,由题意可得结论.
【详解】(1)把时,;时,代入得:
,解得:,;
(2)设第个生产周期创造的利润为万元,由()知,当时,,
∴,
,
,
∵,,
∴当时,取得最大值,最大值为,
∴工厂第个生产周期获得的利润最大,最大的利润是万元;
当时,,
∴,
∴,
则与的函数图象如图所示:
由图象可知,若有且只有个生产周期的利润不小于万元,
∴当,时,,
当,时,,
∴的取值范围.
【点睛】此题考查了一次函数与二次函数在销售问题中的应用,明确一次函数与二次函数的性质并分类讨论是解题的关键.
考点04 投球问题
1.(2025·贵州·中考真题)用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点,运动路径近似为抛物线,且,石块在水面上弹起后第二次与水面接触于点,运动路径近似为抛物线,且.(小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
(1)如图②,当时,若点坐标为,求抛物线的表达式;
(2)在(1)的条件下,若,在水面上有一个截面宽,高的矩形的障碍物,点的坐标为,判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;
(3)小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中,求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)
【答案】(1)
(2)不能,理由见解析
(3)
【分析】(1)利用待定系数法求解即可;
(2)首先得到,然后求出,然后将代入求解判断即可;
(3)首先求出,然后由越小开口越大,越大开口越小,点在和之间(包括这两点)得到当抛物线顶点为点M,且经过点时,开口最大,此时a最大,当抛物线顶点为点P,且经过点时,开口最小,此时a最小,然后分别利用待定系数法求解即可.
【详解】(1)∵当时,
∵点坐标为
∴
∴
∴抛物线的表达式为;
(2)不能,理由如下:
∵,点坐标为
∴
∴
∵点的坐标为,
∴
∴将代入
∴此时石块沿抛物线运动时不能越过障碍物;
(3)∵正方形,
∴
∴如图所示,
∵抛物线开口向下
∴
∵越小开口越大,越大开口越小,点在和之间(包括这两点)
∴由图象可得,当抛物线顶点为点M,且经过点时,开口最大,此时a最大
∴设的表达式为
将代入得,
解得;
∴由图象可得,当抛物线顶点为点P,且经过点时,开口最小,此时a最小
∴设的表达式为
将代入得,
解得;
∴的取值范围为.
【点睛】此题考查了二次函数的应用,待定系数法求二次函数解析式,正方形的性质等知识,数形结合是解题的关键.
2.(2025·江苏连云港·中考真题)如图,小亮同学掷铅球时,铅球沿抛物线运行,其中是铅球离初始位置的水平距离,是铅球离地面的高度.若铅球抛出时离地面的高度为,则铅球掷出的水平距离为 .
【答案】
【分析】本题考查待定系数法求抛物线解析式,二次函数与轴的交点坐标,熟练掌握待定系数法和二次函数与一元二次方程的关系是解题的关键.由题得,代入,得出抛物线的解析式为,令,求解即可,
【详解】解:由题意,,
得,
将代入,
得:,
解得:,
∴,
令,得,
解得:,,
∴为,
故答案为:.
3.(2024·甘肃兰州·中考真题)在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:
水平距离 0 3 4 10 15 20 22 27
竖直高度 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据上表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.
【答案】(1)抛物线的表达式
(2)水火箭距离地面的竖直高度米
【分析】本题主要考查二次函数的性质,
根据题意可设抛物线的表达式,结合体图标可知抛物线的顶点坐标为,代入求解即可;
由题意知,代入抛物线的表达式即可求得水火箭距离地面的竖直高度.
【详解】(1)解:根据题意可知抛物线过原点,设抛物线的表达式,
由表格得抛物线的顶点坐标为,则,解得,
则抛物线的表达式,
(2)解:由题意知,则,
那么,水火箭距离地面的竖直高度米.
4.(2024·青海·中考真题)在如图所示的平面直角坐标系中,有一斜坡,从点O处抛出一个小球,落到点处.小球在空中所经过的路线是抛物线的一部分.
(1)求抛物线的解析式;
(2)求抛物线最高点的坐标;
(3)斜坡上点B处有一棵树,点B是的三等分点,小球恰好越过树的顶端C,求这棵树的高度.
【答案】(1)
(2)
(3)这棵树的高为2
【分析】本题考查了二次函数的应用,其中涉及到待定系数法求二次函数的解析式,二次函数顶点坐标的求解方法,相似三角形的判定和性质,难度适中利用数形结合与方程思想是解题的关键.
(1)利用待定系数法求解即可;
(2)配成顶点式,利用二次函数的性质即可求解;
(3)过点A、B分别作x轴的垂线,证明,利用相似三角形的性质求得,,据此求解即可.
【详解】(1)解:∵点是抛物线上的一点,
把点代入中,得:,
解得,
∴抛物线的解析式为;
(2)解:由(1)得:,
∴抛物线最高点对坐标为;
(3)解:过点A、B分别作x轴的垂线,垂足分别是点E、D,
∵,,
∴,
∴,
又∵点B是的三等分点,
∴,
∵,
∴,,
∴,
解得,
∴,
解得,
∴点C的横坐标为1,
将代入中,,
∴点C的坐标为,
∴,
∴,
答:这棵树的高为2.
5.(2024·天津·中考真题)从地面竖直向上抛出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是.有下列结论:
①小球从抛出到落地需要;
②小球运动中的高度可以是;
③小球运动时的高度小于运动时的高度.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【答案】C
【分析】本题考查二次函数的图像和性质,令解方程即可判断①;配方成顶点式即可判断②;把和代入计算即可判断③.
【详解】解:令,则,解得:,,
∴小球从抛出到落地需要,故①正确;
∵,
∴最大高度为,
∴小球运动中的高度可以是,故②正确;
当时,;当时,;
∴小球运动时的高度大于运动时的高度,故③错误;
故选C.
6.(2024·江西·中考真题)如图,一小球从斜坡O点以一定的方向弹出球的飞行路线可以用二次函数刻画,斜坡可以用一次函数刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如下表:
x 0 1 2 m 4 5 6 7 …
y 0 6 8 n …
(1)①______,______;
②小球的落点是A,求点A的坐标.
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系.
①小球飞行的最大高度为______米;
②求v的值.
【答案】(1)①3,6;②;
(2)①8,②
【分析】本题主要考查二次函数的应用以及从图象和表格中获取数据,
(1)①由抛物线的顶点坐标为可建立过于a,b的二元一次方程组,求出a,b的值即可;②联立两函数解析式求解,可求出交点A的坐标;
(2)①根据第一问可知最大高度为8米;
②将小球飞行高度与飞行时间的函数关系式化简为顶点式即可求得v值.
【详解】(1)解:①根据小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律表可知:抛物线顶点坐标为,
∴,
解得:,
∴二次函数解析式为,
当时,,
解得:或(舍去),
∴,
当时,,
故答案为:3,6.
②联立得:,
解得:或 ,
∴点A的坐标是,
(2)①由题干可知小球飞行最大高度为8米,
故答案为:8;
②,
则,
解得(负值舍去).
7.(2023·浙江·中考真题)根据以下素材,探究完成任务.
如何把实心球掷得更远?
素材1
小林在练习投掷实心球,其示意图如图,第一次练习时,球从点A处被抛出,其路线是抛物线.点A距离地面,当球到OA的水平距离为时,达到最大高度为.
素材2
根据体育老师建议,第二次练习时,小林在正前方处(如图)架起距离地面高为的横线.球从点A处被抛出,恰好越过横线,测得投掷距离.
问题解决
任务1
计算投掷距离 建立合适的直角坐标系,求素材1中的投掷距离.
任务2
探求高度变化 求素材2和素材1中球的最大高度的变化量
任务3
提出训练建议 为了把球掷得更远,请给小林提出一条合理的训练建议.
【答案】任务一:4m;任务二:;任务三:应该尽量提高掷出点的高度、尽量提高掷出点的速度、选择适当的掷出仰角
【分析】任务一:建立直角坐标系,由题意得:抛物线的顶点坐标为,设抛物线的解析式为,过点,利用待定系数法求出解析式,当时求出x的值即可得到;
任务二:建立直角坐标系,求出任务二的抛物线解析式,得到顶点纵坐标,与任务一的纵坐标相减即可;
任务三:根据题意给出合理的建议即可.
【详解】任务一:建立如图所示的直角坐标系,
由题意得:抛物线的顶点坐标为,
设抛物线的解析式为,过点,
∴,
解得,
∴,
当时,,
得(舍去),
∴素材1中的投掷距离为4m;
(2)建立直角坐标系,如图,
设素材2中抛物线的解析式为,
由题意得,过点,
∴,
解得,
∴
∴顶点纵坐标为,
(m),
∴素材2和素材1中球的最大高度的变化量为;
任务三:应该尽量提高掷出点的高度、尽量提高掷出点的速度、选择适当的掷出仰角.
【点睛】此题考查了二次函数的实际应用,求函数解析式,求抛物线与坐标轴的距离,正确理解题意建立恰当的直角坐标系是解题的关键.
8.(2023·内蒙古赤峰·中考真题)乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
水平距离x/
竖直高度y/
(1)在平面直角坐标系中,描出表格中各组数值所对应的点,并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是__________,当乒乓球落在对面球台上时,到起始点的水平距离是__________;
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274,球网高为15.25.现在已经计算出乒乓球恰好过网的击球高度的值约为1.27.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).
【答案】(1)见解析
(2)①;;②
(3)乒乓球恰好落在对面球台边缘点B处时,击球高度的值为
【分析】(1)根据描点法画出函数图象即可求解;
(2)①根据二次函数图象的对称性求得对称轴以及顶点,根据表格数据,可得当时,;
②待定系数法求解析式即可求解;
(3)根据题意,设平移后的抛物线的解析式为,根据题意当时,,代入进行计算即可求解.
【详解】(1)解:如图所示,
(2)①观察表格数据,可知当和时,函数值相等,则对称轴为直线,顶点坐标为,
又抛物线开口向下,可得最高点时,与球台之间的距离是,
当时,,
∴乒乓球落在对面球台上时,到起始点的水平距离是;
故答案为:;.
②设抛物线解析式为,将代入得,
,
解得:,
∴抛物线解析式为;
(3)∵当时,抛物线的解析式为,
设乒乓球恰好落在对面球台边缘点B处时,击球高度的值为,则平移距离为,
∴平移后的抛物线的解析式为,
依题意,当时,,
即,
解得:.
答:乒乓球恰好落在对面球台边缘点B处时,击球高度的值为.
【点睛】本题考查了二次函数的应用,画二次函数图象,二次函数图象的平移,熟练掌握二次函数图象的性质是解题的关键.
考点05 喷水问题
1.(2025·甘肃平凉·中考真题)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是,则水流喷出的最大高度是( )
A. B. C. D.
【答案】B
【分析】本题考查了二次函数的实际应用,正确理解题意、将抛物线转化为顶点式是解题关键;
将抛物线化为顶点式即可解决问题.
【详解】解:∵,
∴当时,;
故选:B.
2.(2023·山东滨州·中考真题)如图,要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为3米,水柱落地处离池中心3米,水管长 米.
【答案】//2.25
【分析】本题考查二次函数的实际应用,根据题意建立平面直角坐标系,设二次函数顶点式,求出二次函数解析式,再求出抛物线与y轴交点坐标即可.
【详解】解:如图,建立平面直角坐标系,
设抛物线的解析式为,
将代入,得,
解得,
∴抛物线的解析式为:,
令,得,
故答案为:.
3.(2023·山东·中考真题)城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽.(结果精确到0.1米)参考数据:
【答案】3.2米
【分析】先以点O为坐标原点,所在直线为x轴,所在直线为y轴,建立平面直角坐标系,则,,设设抛物线的解析式为,把代入,求得,即,再求出点D的坐标,即可求解.
【详解】解:如图,建立平面直角坐标系,
由题意知:,,
∵抛物线的最高点B,
∴设抛物线的解析式为,
把代入,得,
解得,
∴抛物线的解析式为,
令,则,
解得:,
∴,
∴ (米),
答:步行通道的宽的长约为3.2米.
【点睛】本题考查抛物线的实际应用.熟练掌握用待定系数法求抛物线解析式和抛物线的图象性质是解题的关键.
4.(2023·吉林长春·中考真题)年5月8日,商业首航完成——中国民商业运营国产大飞机正式起步.时分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”、是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为米时,两条水柱在物线的顶点H处相遇,此时相遇点H距地面米,喷水口A、B距地面均为4米.若两辆消防车同时后退米,两条水柱的形状及喷水口、到地面的距离均保持不变,则此时两条水柱相遇点距地面 米.
【答案】
【分析】根据题意求出原来抛物线的解析式,从而求得平移后的抛物线解析式,再令求平移后的抛物线与轴的交点即可.
【详解】解:由题意可知:
、、,
设抛物线解析式为:,
将代入解析式,
解得:,
,
消防车同时后退米,即抛物线向左(右)平移米,
平移后的抛物线解析式为:,
令,解得:,
故答案为:.
【点睛】本题考查了待定系数法求抛物线解析式、函数图像的平移及坐标轴的交点;解题的关键是求得移动前后抛物线的解析式.
1.(2025·内蒙古·中考真题)问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为.在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴.建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
2.(2025·江苏连云港·中考真题)一块直角三角形木板,它的一条直角边长,面积为.
(1)甲、乙两人分别按图1、图2用它设计一个正方形桌面,请说明哪个正方形面积较大;
(2)丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积与的长之间的函数表达式,并分别求出面积的最大值.
3.(2025·广西·中考真题)综合与实践
树人中学组织一次“爱心义卖”活动.九(5)班分配到了一块矩形义卖区和一把遮阳伞,遮阳伞在地面上的投影是一个平行四边形(如图1)
初始时,矩形义卖区与遮阳伞投影的平面图如图2所示,在上,,,,,,由于场地限制,参加义卖的同学只能左右平移遮阳伞.在移动过程中,也随之移动(始终在边所在直线上),且形状大小保持不变,但落在义卖区内的部分(遮阳区)会呈现不同的形状.如图3为移动到落在上的情形.
【问题提出】
西西同学打算用数学方法,确定遮阳区面积最大时的位置.
设遮阳区的面积为,从初始时向右移动的距离为.
【直观感知】(1)从初始起右移至图3情形的过程中,随的增大如何变化?
【初步探究】(2)求图3情形的与的值;
【深入研究】(3)从图3情形起右移至与重合,求该过程中关于的解析式;
【问题解决】(4)当遮阳区面积最大时,向右移动了多少?(直接写出结果)
4.(2024·湖北·中考真题)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
5.(2024·山东潍坊·中考真题)【问题提出】
在绿化公园时,需要安装一定数量的自动喷洒装置,定时喷水养护,某公司准备在一块边长为的正方形草坪(如图1)中安装自动喷洒装置,为了既节约安装成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方案.
说明:一个自动喷洒装置的喷洒范围是半径为的圆面.喷洒覆盖率,为待喷洒区域面积,为待喷洒区域中的实际喷洒面积.
【数学建模】
这个问题可以转化为用圆面覆盖正方形面积的数学问题.
【探索发现】
(1)如图2,在该草坪中心位置设计安装1个喷洒半径为的自动喷洒装置,该方案的喷洒覆盖率______.
(2)如图3,在该草坪内设计安装4个喷洒半径均为的自动喷洒装置;如图4,设计安装9个喷洒半径均为3m的自动喷洒装置;,以此类推,如图5,设计安装个喷洒半径均为的自动喷洒装置.与(1)中的方案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒覆盖率?请判断并给出理由.
(3)如图6所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,且使得该草坪的喷洒覆盖率.已知正方形各边上依次取点F,G,H,E,使得,设,的面积为,求关于的函数表达式,并求当取得最小值时的值.
【问题解决】
(4)该公司现有喷洒半径为的自动喷洒装置若干个,至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率?(直接写出结果即可)
6.(2023·山东潍坊·中考真题)工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
考点02 拱桥问题
1.(2025·新疆·中考真题)天山胜利隧道预计于2025年建成通车,它将成为世界上最长的高速公路隧道,能大大提升区域交通效率,促进经济发展.如图是隧道截面图,其轮廓可近似看作是抛物线的一部分.若隧道底部宽12米,高8米,按照如图所示的方式建立平面直角坐标系.
(1)求抛物线的函数解析式;
(2)该隧道设计为单向双车道通行,车辆顶部在竖直方向上与隧道的空隙不少于0.5米,当两辆车在隧道内并排行驶时,需沿中心线两侧行驶,且两车至少间隔2米(中心线宽度不计).若宽3米,高3.5米的两辆车并排行驶,能否安全通过?请说明理由.
2.(2025·陕西·中考真题)某景区大门上半部分的截面示意图如图所示,顶部,左、右门洞,均呈抛物线型,水平横梁,的最高点到的距离,,关于所在直线对称.,,为框架,点,在上,点,分别在,上,,,.以为原点,以所在直线为轴,以所在直线为轴,建立平面直角坐标系.
(1)求抛物线的函数表达式;
(2)已知抛物线的函数表达式为,,求的长.
3.(2024·陕西·中考真题)一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
4.(2023·贵州·中考真题)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
考点03 销售问题
1.(2025·四川内江·中考真题)2025年春节期间,我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录,商家推出A、B两款“哪吒”文旅纪念品.已知购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元.
(1)求A、B两款“哪吒”纪念品每个进价分别为多少元?
(2)根据网上预约的情况,如果该商家计划用不超过12000元的资金购进A、B两款“哪吒”纪念品共400个,那么至少需要购进B款纪念品多少个?
(3)在销售中,该商家发现每个A款纪念品售价60元时,可售出200个,售价每增加1元,销售量将减少5个.设每个A款纪念品售价元,W表示该商家销售A款纪念品的利润(单位:元),求W关于a的函数表达式,并求出W的最大值.
2.(2025·四川南充·中考真题)学校计划租用客车送师生到某红色基地,参加主题为“缅怀先烈,强国有我”的研学活动,请阅读下列材料,并完成相关问题.
材料一 租车公司有A,B两种型号的客车可供租用,在每辆车满员情况下,每辆A型客车比每辆B型客车多载客15人;用A型客车载客600人与用B型客车载客450人的车辆数相同.
材料二 A型客车租车费用为3200元/辆;B型客车租车费用为3000元/辆. 优惠方案:租用A型客车m辆,租车费用元/辆; 租用B型客车,租车费用打八折.
材料三 租车公司最多提供8辆A型客车; 学校参加研学活动师生共有530人,租用A,B两种型号客车共10辆.
(1)A,B两种型号的客车每辆载客量分别是多少?
(2)本次研学活动学校的最少租车费用是多少?
3.(2024·山东青岛·中考真题)5月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季.为了解樱桃的收益情况,从第1天销售开始,小明对自己家的两处樱桃园连续15天的销售情况进行了统计与分析:
A樱桃园 第x天的单价、销售量与x的关系如下表: 单价(元/盒)销售量(盒)第1天5020第2天4830第3天4640第4天4450………第x天10x+10
第x天的单价与x近似地满足一次函数关系,已知每天的固定成本为745元. B樱桃园 第x天的利润(元)与x的关系可以近似地用二次函数刻画,其图象如图:
(1)A樱桃园第x天的单价是______元/盒(用含x的代数式表示);
(2)求A樱桃园第x天的利润(元)与x的函数关系式;(利润单价销售量固定成本)
(3)①与x的函数关系式是______;
②求第几天两处樱桃园的利润之和(即)最大,最大是多少元?
(4)这15天中,共有______天B樱桃园的利润比A樱桃园的利润大.
4.(2024·黑龙江大庆·中考真题)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的天中,第天且为整数)的售价为(元千克).当时,;当时,.销量(千克)与的函数关系式为,已知该产品第天的售价为元千克,第天的售价为元千克,设第天的销售额为(元).
(1) ,_____;
(2)写出第天的销售额与之间的函数关系式;
(3)求在试销售的天中,共有多少天销售额超过元?
5.(2024·贵州·中考真题)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
6.(2024·江苏盐城·中考真题)请根据以下素材,完成探究任务.
制定加工方案
生产背景 背景1 ◆某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式. ◆因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或“雅”服装1件,或“正”服装1件. ◆要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
背景2 每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为: ①“风”服装:24元/件; ②“正”服装:48元/件; ③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整理 现安排x名工人加工“雅”服装,y名工人加工“风”服装,列表如下: 服装种类加工人数(人)每人每天加工量(件)平均每件获利(元)风y224雅x1正148
探究任务 任务1 探寻变量关系 求x、y之间的数量关系.
任务2 建立数学模型 设该工厂每天的总利润为w元,求w关于x的函数表达式.
任务3 拟定加工方案 制定使每天总利润最大的加工方案.
7.(2023·湖北黄石·中考真题)某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元/件.设第个生产周期设备的售价为万元/件,售价与之间的函数解析式是,其中是正整数.当时,;当时,.
(1)求,的值;
(2)设第个生产周期生产并销售完设备的数量为件,且y与x满足关系式.
当时,工厂第几个生产周期获得的利润最大 最大的利润是多少万元
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.
考点04 投球问题
1.(2025·贵州·中考真题)用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点,运动路径近似为抛物线,且,石块在水面上弹起后第二次与水面接触于点,运动路径近似为抛物线,且.(小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
(1)如图②,当时,若点坐标为,求抛物线的表达式;
(2)在(1)的条件下,若,在水面上有一个截面宽,高的矩形的障碍物,点的坐标为,判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;
(3)小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中,求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)
2.(2025·江苏连云港·中考真题)如图,小亮同学掷铅球时,铅球沿抛物线运行,其中是铅球离初始位置的水平距离,是铅球离地面的高度.若铅球抛出时离地面的高度为,则铅球掷出的水平距离为 .
3.(2024·甘肃兰州·中考真题)在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:
水平距离 0 3 4 10 15 20 22 27
竖直高度 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据上表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.
4.(2024·青海·中考真题)在如图所示的平面直角坐标系中,有一斜坡,从点O处抛出一个小球,落到点处.小球在空中所经过的路线是抛物线的一部分.
(1)求抛物线的解析式;
(2)求抛物线最高点的坐标;
(3)斜坡上点B处有一棵树,点B是的三等分点,小球恰好越过树的顶端C,求这棵树的高度.
5.(2024·天津·中考真题)从地面竖直向上抛出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是.有下列结论:
①小球从抛出到落地需要;
②小球运动中的高度可以是;
③小球运动时的高度小于运动时的高度.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6.(2024·江西·中考真题)如图,一小球从斜坡O点以一定的方向弹出球的飞行路线可以用二次函数刻画,斜坡可以用一次函数刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如下表:
x 0 1 2 m 4 5 6 7 …
y 0 6 8 n …
(1)①______,______;
②小球的落点是A,求点A的坐标.
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系.
①小球飞行的最大高度为______米;
②求v的值.
7.(2023·浙江·中考真题)根据以下素材,探究完成任务.
如何把实心球掷得更远?
素材1
小林在练习投掷实心球,其示意图如图,第一次练习时,球从点A处被抛出,其路线是抛物线.点A距离地面,当球到OA的水平距离为时,达到最大高度为.
素材2
根据体育老师建议,第二次练习时,小林在正前方处(如图)架起距离地面高为的横线.球从点A处被抛出,恰好越过横线,测得投掷距离.
问题解决
任务1
计算投掷距离 建立合适的直角坐标系,求素材1中的投掷距离.
任务2
探求高度变化 求素材2和素材1中球的最大高度的变化量
任务3
提出训练建议 为了把球掷得更远,请给小林提出一条合理的训练建议.
8.(2023·内蒙古赤峰·中考真题)乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
水平距离x/
竖直高度y/
(1)在平面直角坐标系中,描出表格中各组数值所对应的点,并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是__________,当乒乓球落在对面球台上时,到起始点的水平距离是__________;
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274,球网高为15.25.现在已经计算出乒乓球恰好过网的击球高度的值约为1.27.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).
考点05 喷水问题
1.(2025·甘肃平凉·中考真题)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是,则水流喷出的最大高度是( )
A. B. C. D.
2.(2023·山东滨州·中考真题)如图,要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为3米,水柱落地处离池中心3米,水管长 米.
3.(2023·山东·中考真题)城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽.(结果精确到0.1米)参考数据:
4.(2023·吉林长春·中考真题)年5月8日,商业首航完成——中国民商业运营国产大飞机正式起步.时分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”、是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为米时,两条水柱在物线的顶点H处相遇,此时相遇点H距地面米,喷水口A、B距地面均为4米.若两辆消防车同时后退米,两条水柱的形状及喷水口、到地面的距离均保持不变,则此时两条水柱相遇点距地面 米.
答案解析
考点01 图形问题
1.(2025·内蒙古·中考真题)问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为.在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴.建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
【答案】(1),,
(2)抛物线和的顶点坐标分别为,, 的表达式为;的表达式为;
(3)
【分析】(1)由矩形性质可得,,,,即可得出坐标;
(2)由装置整体图案为轴对称图形,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,由矩形中,抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,即可得出抛物线和的顶点坐标分别为,,分别设抛物线和的表达式为,,分别将将和代入求解即可;
(3)由装置整体图案为轴对称图形,得出,,证明轴,设,则,,则,求得,由抛物线对称性可得.
【详解】(1)解:∵矩形的边,,
∴,,,,
∴,,;
(2)解:∵装置整体图案为轴对称图形,
如图,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,
结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,
∴四边形是矩形,
∴,
∵抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,
∴,,
∴抛物线和的顶点坐标分别为,,
分别设抛物线和的表达式为,,
将代入,
解得,
则抛物线的表达式为;
将代入,
解得;
则抛物线的表达式为;
(3)解:∵装置整体图案为轴对称图形,
∴,,
∵轴,
∴轴,
∵是矩形,
∴,
∴轴,
∴,
设,
∴,,
∴,
解得:或(在对称轴右侧,舍),
∴,
由抛物线对称性可得.
【点睛】本题考查二次函数的图象与几何综合,矩形的性质,平面直角坐标系,待定系数法求二次函数的解析式,二次函数的图象与性质,熟练掌握相关性质是解题的关键.
2.(2025·江苏连云港·中考真题)一块直角三角形木板,它的一条直角边长,面积为.
(1)甲、乙两人分别按图1、图2用它设计一个正方形桌面,请说明哪个正方形面积较大;
(2)丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积与的长之间的函数表达式,并分别求出面积的最大值.
【答案】(1)图1的正方形面积较大
(2)在图3中,,当时,长方形的面积有最大值为;在图4中,,当时,长方形的面积有最大值为
【分析】本题考查了相似三角形的判定与性质,勾股定理,正方形的性质,二次函数的应用,正确掌握相关性质内容是解题的关键.
(1)先运用勾股定理算出,再运用正方形的性质分别证明,,,然后代入数值化简得,进行计算得,然后进行比较,即可作答.
(2)与(1)同理证明,则长方形的面积,结合二次函数的图象性质得当时,长方形的面积有最大值为.,然后证明,,再把数值代入长方形的面积,化简得,结合二次函数的图象性质进行作答即可.
【详解】(1)解:∵,面积为,
∴,
∴.
设正方形的边长为,
∵四边形是正方形
∴,,
∵
∴
得,
即,
解得.
∵四边形是正方形
∴,
∴
∴,
得,
即,
∴.
,
∵
∴,
得,
即,
解得.
∵,
∴图1的正方形面积较大.
(2)解:∵四边形是长方形
∴,,
∵
∴;
得,
则,,
∴长方形的面积,
∵
∴开口向下,
当时,长方形的面积有最大值为.
在图4中,同理得,
得,
∴,,
同理得,
得,
则,
∴长方形的面积,
∵
∴开口向下,
∴当时,长方形的面积有最大值为.
3.(2025·广西·中考真题)综合与实践
树人中学组织一次“爱心义卖”活动.九(5)班分配到了一块矩形义卖区和一把遮阳伞,遮阳伞在地面上的投影是一个平行四边形(如图1)
初始时,矩形义卖区与遮阳伞投影的平面图如图2所示,在上,,,,,,由于场地限制,参加义卖的同学只能左右平移遮阳伞.在移动过程中,也随之移动(始终在边所在直线上),且形状大小保持不变,但落在义卖区内的部分(遮阳区)会呈现不同的形状.如图3为移动到落在上的情形.
【问题提出】
西西同学打算用数学方法,确定遮阳区面积最大时的位置.
设遮阳区的面积为,从初始时向右移动的距离为.
【直观感知】(1)从初始起右移至图3情形的过程中,随的增大如何变化?
【初步探究】(2)求图3情形的与的值;
【深入研究】(3)从图3情形起右移至与重合,求该过程中关于的解析式;
【问题解决】(4)当遮阳区面积最大时,向右移动了多少?(直接写出结果)
【答案】(1)随的增大而增大;(2),;(3);(4)
【分析】(1)根据矩形的性质得,根据平行四边形的面积公式得,然后分别求出当时,当时,关于的解析式,即可得出结论;
(2)根据(1)的结论可得答案;
(3)当时,如图,设向右移动后得到,设交于点,交于点,交于点,则,,
此时遮阳区的面积为六边形的面积,推出,,得,,再根据即可得出结论;
(4)分别确定:当时,当时,当时,各个范围内的最大值,即可得出结论.
【详解】解:(1)∵四边形是矩形,四边形是平行四边形,,,,在边所在直线上,
∴,,,
又∵如图2,在上,,,
∴,
,
当时,如图,设交于点,交于点,则,
此时遮阳区的面积为的面积,
∵,
∴,,
∴,
∴,
∴,
∴当时,随的增大而增大,的值从增大到;
当时,如图,设交于点,则,,,
此时遮阳区的面积为四边形的面积,
∵,
∴四边形为梯形,
∴,
∴当时,随的增大而增大,的值从增大到;
综上所述,从初始起右移至图3情形的过程中,随的增大而增大;
(2)如图3,此时点落在上,则,
由(1)知:当时,;
∴图3情形时,,;
(3)当时,如图,设向右移动后得到,设交于点,交于点,交于点,则,,
此时遮阳区的面积为六边形的面积,
∴,,,
∴,,
∴,,
∴,,
∴
,
∴从图3情形起右移至与重合,该过程中关于的解析式为;
(4)当时,,
当时,的最大值为:;
当时,,
当时,的最大值为:;
当时,,
∵
∴当时,的最大值为:,
综上所述,当时,取得最大值,最大值为,
∴当遮阳区面积最大时,向右移动了.
【点睛】本题考查平移的性质,矩形的性质,平行四边形的性质,锐角三角函数的定义,列函数关系式,二次函数的最值,等积变换等知识点,利用分类讨论的思想及数形结合的思想解决问题是解题的关键.
4.(2024·湖北·中考真题)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到吗?如果能,求x的值;如果不能,请说明理由.
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
【答案】(1),
(2)
(3)当时,实验田的面积S最大,最大面积是
【分析】本题考查了矩形的性质,二次函数的实际应用,计算的取值范围是解题的关键.
(1)根据,求出与的函数解析式,根据矩形面积公式求出与的函数解析式;
(2)先求出的取值范围,再将代入函数中,求出的值;
(3)将与的函数配成顶点式,求出的最大值.
【详解】(1)解:,
,
,
;
(2),
,
,
,
当时,,
,
,
,
当时,矩形实验田的面积能达到;
(3),
当时,有最大值.
5.(2024·山东潍坊·中考真题)【问题提出】
在绿化公园时,需要安装一定数量的自动喷洒装置,定时喷水养护,某公司准备在一块边长为的正方形草坪(如图1)中安装自动喷洒装置,为了既节约安装成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方案.
说明:一个自动喷洒装置的喷洒范围是半径为的圆面.喷洒覆盖率,为待喷洒区域面积,为待喷洒区域中的实际喷洒面积.
【数学建模】
这个问题可以转化为用圆面覆盖正方形面积的数学问题.
【探索发现】
(1)如图2,在该草坪中心位置设计安装1个喷洒半径为的自动喷洒装置,该方案的喷洒覆盖率______.
(2)如图3,在该草坪内设计安装4个喷洒半径均为的自动喷洒装置;如图4,设计安装9个喷洒半径均为3m的自动喷洒装置;,以此类推,如图5,设计安装个喷洒半径均为的自动喷洒装置.与(1)中的方案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒覆盖率?请判断并给出理由.
(3)如图6所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,且使得该草坪的喷洒覆盖率.已知正方形各边上依次取点F,G,H,E,使得,设,的面积为,求关于的函数表达式,并求当取得最小值时的值.
【问题解决】
(4)该公司现有喷洒半径为的自动喷洒装置若干个,至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率?(直接写出结果即可)
【答案】(1);(2)不能,理由见解析;(3);当取得最小值时;(4)
【分析】(1)根据定义,分别计算圆的面积与正方形的面积,即可求解;
(2)根据(1)的方法求得喷洒覆盖率即可求解;
(3)根据勾股定理求得的关系,进而根据圆的面积公式得出函数关系式,根据二次函数的性质,即可求解;
(4)根据(3)的结论可得当圆为正方形的外接圆时,面积最小,则求得半径为的圆的内接正方形的边长为,进而将草坪分为个正方形,即可求解.
【详解】(1)当喷洒半径为时,喷洒的圆面积.
正方形草坪的面积.
故喷洒覆盖率.
(2)对于任意的,喷洒面积,而草坪面积始终为.
因此,无论取何值,喷洒覆盖率始终为.
这说明增加装置个数同时减小喷洒半径,对提高喷洒覆盖率不起作用.
(3)如图所示,连接,
要使喷洒覆盖率,即要求,其中为草坪面积,为喷洒面积.
∴都经过正方形的中心点,
在中,,,
∵
∴,
在中,
∴
∴
∴当时,取得最小值,此时
解得:
(4)由(3)可得,当的面积最小时,此时圆为边长为的正方形的外接圆,
则当时,圆的内接正方形的边长为
而草坪的边长为,,即将草坪分为个正方形,将半径为的自动喷洒装置放置于9个正方形的中心,此时所用装置个数最少,
∴至少安装个这样的喷洒装置可使该草坪的喷洒覆盖率
【点睛】本题考查了正方形与圆综合问题,二次函数的应用;本题要求我们先理解和计算喷洒覆盖率,然后通过调整喷洒装置的数量和喷洒半径来分析喷洒覆盖率的变化,最后在一个特定的条件下找出喷洒面积和喷洒半径之间的函数关系.解决此类问题的关键在于将实际问题转化为数学问题,即如何将喷洒覆盖率的计算问题转化为面积计算和函数求解问题.同时,在解决具体问题时,需要灵活运用已知的数学知识,如圆的面积公式,正方形面积公式,以及函数解析式求解等.最后,还需要注意将数学计算结果还原为实际问题的解决方案.
6.(2023·山东潍坊·中考真题)工匠师傅准备从六边形的铁皮中,裁出一块矩形铁皮制作工件,如图所示.经测量,,与之间的距离为2米,米,米,,.,,是工匠师傅画出的裁剪虚线.当的长度为多少时,矩形铁皮的面积最大,最大面积是多少?
【答案】当的长度为米时,矩形铁皮的面积最大,最大面积是平方米
【分析】连接,分别交于点,交于点,先判断出四边形是矩形,从而可得,再判断出四边形和四边形都是矩形,从而可得米,,然后设矩形的面积为平方米,米,则米,米,利用矩形的面积公式可得关于的二次函数,最后利用二次函数的性质求解即可得.
【详解】解:如图,连接,分别交于点,交于点,
,
,
米,
四边形是平行四边形,
又,
四边形是矩形,
,,
,
,
四边形是矩形,
,
四边形和四边形都是矩形,
米,,
和都是等腰直角三角形,
,
,
设矩形的面积为平方米,米,则米,米,
米,
米,
,
又,与之间的距离为2米,米,
,
由二次函数的性质可知,当时,随的增大而增大;当时,随的增大而减小,
则当时,取得最大值,最大值为,
答:当的长度为米时,矩形铁皮的面积最大,最大面积是平方米.
【点睛】本题考查了二次函数的几何应用、矩形的判定与性质等知识点,熟练掌握二次函数的性质是解题关键.
考点02 拱桥问题
1.(2025·新疆·中考真题)天山胜利隧道预计于2025年建成通车,它将成为世界上最长的高速公路隧道,能大大提升区域交通效率,促进经济发展.如图是隧道截面图,其轮廓可近似看作是抛物线的一部分.若隧道底部宽12米,高8米,按照如图所示的方式建立平面直角坐标系.
(1)求抛物线的函数解析式;
(2)该隧道设计为单向双车道通行,车辆顶部在竖直方向上与隧道的空隙不少于0.5米,当两辆车在隧道内并排行驶时,需沿中心线两侧行驶,且两车至少间隔2米(中心线宽度不计).若宽3米,高3.5米的两辆车并排行驶,能否安全通过?请说明理由.
【答案】(1)
(2)能安全通过,见解析
【分析】本题考查了二次函数的实际应用,正确理解题意是解题的关键.
(1)先得到顶点坐标,然后设顶点式,再代入即可求解,继而得到函数解析式;
(2)先求出点坐标,然后求出点距离抛物线的距离,然后减去车辆的高度,得到的差值与比较即可.
【详解】(1)解:由题意得,顶点为,即,
设抛物线的解析式为:
代入点得,
解得:,
∴抛物线解析式为;
(2)解:能安全通过,理由如下:
如图,
由题意得:,
将代入,
则,
∵,
∴能安全通过.
2.(2025·陕西·中考真题)某景区大门上半部分的截面示意图如图所示,顶部,左、右门洞,均呈抛物线型,水平横梁,的最高点到的距离,,关于所在直线对称.,,为框架,点,在上,点,分别在,上,,,.以为原点,以所在直线为轴,以所在直线为轴,建立平面直角坐标系.
(1)求抛物线的函数表达式;
(2)已知抛物线的函数表达式为,,求的长.
【答案】(1)
(2)
【分析】本题考查了二次函数的图象性质,二次函数的解析式,因式分解法进行解方程,正确掌握相关性质内容是解题的关键.
(1)理解题意,先设抛物线的函数表达式为,结合二次函数的对称性得,再代入进行求解,即可作答.
(2)理解题意,得出,再结合抛物线,的函数表达式分别为,,代入,整理得,再解方程,可作答.
【详解】(1)解:∵,
∴抛物线的顶点坐标为,
设抛物线的函数表达式为,
∵,
∴结合二次函数的对称性得,
将代入,
得
则,
∴;
(2)解:由(1)得抛物线的函数表达式,
∵,,.,且抛物线的函数表达式为,
∴,
整理得,
∴,
∴,
解得,
∴.
3.(2024·陕西·中考真题)一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
【答案】(1);
(2)的长为.
【分析】本题考查了二次函数的应用,待定系数法求二次函数解析式,根据题意求得函数解析式是解题的关键.
(1)根据题意设缆索所在抛物线的函数表达式为,把代入求解即可;
(2)根据轴对称的性质得到缆索所在抛物线的函数表达式为,由,把代入求得,,据此求解即可.
【详解】(1)解:由题意得顶点P的坐标为,点A的坐标为,
设缆索所在抛物线的函数表达式为,
把代入得,
解得,
∴缆索所在抛物线的函数表达式为;
(2)解:∵缆索所在抛物线与缆索所在抛物线关于y轴对称,
∴缆索所在抛物线的函数表达式为,
∵,
∴把代入得,,
解得,,
∴或,
∵,
∴的长为.
4.(2023·贵州·中考真题)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
【答案】(1)
(2)点的坐标为
(3)
【分析】(1)设抛物线的解析式为,将,代入即可求解;
(2)点B关于y轴的对称点,则,求出直线与y轴的交点坐标即可;
(3)分和两种情况,根据最小值大于等于9列不等式,即可求解.
【详解】(1)解:抛物线的对称轴与y轴重合,
设抛物线的解析式为,
,,
,,
将,代入,得:
,
解得,
抛物线的解析式为;
(2)解: 抛物线的解析式为,点到对称轴的距离是1,
当时,,
,
作点B关于y轴的对称点,
则,,
,
当,,A共线时,拉杆长度之和最短,
设直线的解析式为,
将,代入,得,
解得,
直线的解析式为,
当时,,
点的坐标为,位置如下图所示:
(3)解:中,
抛物线开口向下,
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
当时,
在范围内,当时,y取最小值,最小值为:
则,
解得,
;
综上可知,或,
的取值范围为.
【点睛】本题考查二次函数的实际应用,涉及求二次函数解析式,求一次函数解析式,根据对称性求线段的最值,抛物线的增减性等知识点,解题的关键是熟练掌握二次函数的图象和性质,第3问注意分情况讨论.
考点03 销售问题
1.(2025·四川内江·中考真题)2025年春节期间,我国国产动画电影《哪吒之魔童闹海》刷新了中国电影票房的新纪录,商家推出A、B两款“哪吒”文旅纪念品.已知购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元.
(1)求A、B两款“哪吒”纪念品每个进价分别为多少元?
(2)根据网上预约的情况,如果该商家计划用不超过12000元的资金购进A、B两款“哪吒”纪念品共400个,那么至少需要购进B款纪念品多少个?
(3)在销售中,该商家发现每个A款纪念品售价60元时,可售出200个,售价每增加1元,销售量将减少5个.设每个A款纪念品售价元,W表示该商家销售A款纪念品的利润(单位:元),求W关于a的函数表达式,并求出W的最大值.
【答案】(1)A款“哪吒”纪念品每个进价为40元,B款“哪吒”纪念品每个进价为20元;
(2)至少需要购进B款纪念品200个
(3),W的最大值为4500
【分析】本题主要考查了二元一次方程组的实际应用,二次函数的实际应用,一元一次不等式的实际应用,正确理解题意列出方程组,函数关系式和不等式是解题的关键.
(1)设A款“哪吒”纪念品每个进价为x元,B款“哪吒”纪念品每个进价为y元,根据购进A款200个,B款300个,需花费14000元;购进A款100个,B款200个,需花费8000元建立方程组求解即可;
(2)设需要购进B款纪念品m个,则需要购进A款纪念品个,根据购买资金不超过12000元建立不等式求解即可;
(3)根据题意可得每个A款纪念品的利润为元,销售量为个,据此列出W关于a的二次函数关系式,再利用二次函数的性质求出W的最大值即可.
【详解】(1)解:设A款“哪吒”纪念品每个进价为x元,B款“哪吒”纪念品每个进价为y元,
由题意得,,
解得,
答:A款“哪吒”纪念品每个进价为40元,B款“哪吒”纪念品每个进价为20元;
(2)解:设需要购进B款纪念品m个,则需要购进A款纪念品个,
由题意得,,
解得,
∴m的最小值为200,
答:至少需要购进B款纪念品200个;
(3)解:由题意得,
,
∵,
∴当,即时,W最大,最大值为4500.
2.(2025·四川南充·中考真题)学校计划租用客车送师生到某红色基地,参加主题为“缅怀先烈,强国有我”的研学活动,请阅读下列材料,并完成相关问题.
材料一 租车公司有A,B两种型号的客车可供租用,在每辆车满员情况下,每辆A型客车比每辆B型客车多载客15人;用A型客车载客600人与用B型客车载客450人的车辆数相同.
材料二 A型客车租车费用为3200元/辆;B型客车租车费用为3000元/辆. 优惠方案:租用A型客车m辆,租车费用元/辆; 租用B型客车,租车费用打八折.
材料三 租车公司最多提供8辆A型客车; 学校参加研学活动师生共有530人,租用A,B两种型号客车共10辆.
(1)A,B两种型号的客车每辆载客量分别是多少?
(2)本次研学活动学校的最少租车费用是多少?
【答案】(1)A型客车每辆载客量为60人,B型客车每辆载客量为45人
(2)本次研学活动学校最少租车费用为27 000元
【分析】本题主要考查了分式方程的应用,二次函数的实际应用,根据题意得到等量关系式是解题的关键.
(1)设A型客车每辆载客量为人,根据题意列出方程,求解即可;
(2)设租A型客车辆,B型客车辆,租车总费用,根据材料三先求出m的取值范围,再列出w关于m的函数关系式,结合二次函数的性质解答即可.
【详解】(1)解:设A型客车每辆载客量为人,根据题意得:
.
解之得.
经检验:是方程的根,且符合题意,
答:A型客车每辆载客量为60人,B型客车每辆载客量为45人.
(2)解:设租A型客车辆,B型客车辆,租车总费用,则
.
解之得.
.
∵,且对称轴为,
∴时,随着的增大而增大.
∵取正整数,且,
∴当时,最小值为27000(元).
∴本次研学活动学校最少租车费用为27000元
3.(2024·山东青岛·中考真题)5月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季.为了解樱桃的收益情况,从第1天销售开始,小明对自己家的两处樱桃园连续15天的销售情况进行了统计与分析:
A樱桃园 第x天的单价、销售量与x的关系如下表: 单价(元/盒)销售量(盒)第1天5020第2天4830第3天4640第4天4450………第x天10x+10
第x天的单价与x近似地满足一次函数关系,已知每天的固定成本为745元. B樱桃园 第x天的利润(元)与x的关系可以近似地用二次函数刻画,其图象如图:
(1)A樱桃园第x天的单价是______元/盒(用含x的代数式表示);
(2)求A樱桃园第x天的利润(元)与x的函数关系式;(利润单价销售量固定成本)
(3)①与x的函数关系式是______;
②求第几天两处樱桃园的利润之和(即)最大,最大是多少元?
(4)这15天中,共有______天B樱桃园的利润比A樱桃园的利润大.
【答案】(1)
(2)
(3)①;②第10天两处樱桃园的利润之和(即)最大,最大是4800元;
(4)4
【分析】本题主要考查了二次函数的实际应用,一次函数的实际应用:
(1)设出对应的函数解析式,利用待定系数法求解即可;
(2)根据(1)所求结合利润单价销售量固定成本进行求解即可;
(3)①利用待定系数法求解即可;②根据前面所求求出的结果,再利用二次函数的性质求解即可;
(4)根据题意建立不等式,求出不等式的正整数解即可得到答案.
【详解】(1)解:第天的单价与满足的一次函数关系式为,
把代入中得,
∴,
∴第天的单价与满足的一次函数关系式为,
∴A樱桃园第x天的单价是元/盒,
故答案为:;
(2)解:由题意得,
(3)解:①把代入中得:,
解得,
∴;
②∵,,
∴
,
∵,且(x为正整数),
∴当时,有最大值,最大值为4800,
∴第10天两处樱桃园的利润之和(即)最大,最大是4800元;
(4)解:当时,则,
∴,
∴,
∴,
∵x的正整数解有4个,
∴这15天中,共有4天B樱桃园的利润比A樱桃园的利润大.
4.(2024·黑龙江大庆·中考真题)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的天中,第天且为整数)的售价为(元千克).当时,;当时,.销量(千克)与的函数关系式为,已知该产品第天的售价为元千克,第天的售价为元千克,设第天的销售额为(元).
(1) ,_____;
(2)写出第天的销售额与之间的函数关系式;
(3)求在试销售的天中,共有多少天销售额超过元?
【答案】(1),
(2)
(3)在试销售的天中,共有天销售额超过元
【分析】本题考查了一次函数与二次函数的综合应用;
(1)待定系数法求解析式,即可求解;
(2)根据销售额等于销量乘以售价,分段列出函数关系式,即可求解;
(3)根据题意,根据,列出方程,解方程,即可求解.
【详解】(1)解:依题意,将,代入,
∴
解得:
∴
故答案为:,.
(2)解:依题意,
当时,
当时,
∴
(3)解:依题意,当时,
当时,
解得:
为正整数,
∴第天至第天,销售额超过元
(天)
答:在试销售的天中,共有天销售额超过元
5.(2024·贵州·中考真题)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
【答案】(1)
(2)糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元
(3)2
【分析】本题考查了二次函数的应用,解题的关键是:
(1)利用待定系数法求解即可;
(2)设日销售利润为w元,根据利润=单件利润×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可;
(3)设日销售利润为w元,根据利润=单件利润×销售量-m×销售量求出w关于x的函数表达式,然后利用二次函数的性质求解即可.
【详解】(1)解∶设y与x的函数表达式为,
把,;,代入,得,
解得,
∴y与x的函数表达式为;
(2)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为450,
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元;
(3)解:设日销售利润为w元,
根据题意,得
,
∴当时,有最大值为,
∵糖果日销售获得的最大利润为392元,
∴,
化简得
解得,
当时,,
则每盒的利润为:,舍去,
∴m的值为2.
6.(2024·江苏盐城·中考真题)请根据以下素材,完成探究任务.
制定加工方案
生产背景 背景1 ◆某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式. ◆因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或“雅”服装1件,或“正”服装1件. ◆要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
背景2 每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为: ①“风”服装:24元/件; ②“正”服装:48元/件; ③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整理 现安排x名工人加工“雅”服装,y名工人加工“风”服装,列表如下: 服装种类加工人数(人)每人每天加工量(件)平均每件获利(元)风y224雅x1正148
探究任务 任务1 探寻变量关系 求x、y之间的数量关系.
任务2 建立数学模型 设该工厂每天的总利润为w元,求w关于x的函数表达式.
任务3 拟定加工方案 制定使每天总利润最大的加工方案.
【答案】任务1:;任务2:;任务3:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”服装,即可获得最大利润
【分析】题目主要考查一次函数及二次函数的应用,理解题意,根据二次函数的性质求解是解题关键.
任务1:根据题意安排x名工人加工“雅”服装,y名工人加工“风”服装,得出加工“正”服装的有人,然后利用“正”服装总件数和“风”服装相等,得出关系式即可得出结果;
任务2:根据题意得:“雅”服装每天获利为:,然后将2种服装的获利求和即可得出结果;
任务3:根据任务2结果化为顶点式,然后结合题意,求解即可.
【详解】解:任务1:根据题意安排70名工人加工一批夏季服装,
∵安排x名工人加工“雅”服装,y名工人加工“风”服装,
∴加工“正”服装的有人,
∵“正”服装总件数和“风”服装相等,
∴,
整理得:;
任务2:根据题意得:“雅”服装每天获利为:,
∴,
整理得:
∴
任务3:由任务2得,
∴当时,获得最大利润,
,
∴,
∵开口向下,
∴取或,
当时,,不符合题意;
当时,,符合题意;
∴,
综上:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”服装,即可获得最大利润.
7.(2023·湖北黄石·中考真题)某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元/件.设第个生产周期设备的售价为万元/件,售价与之间的函数解析式是,其中是正整数.当时,;当时,.
(1)求,的值;
(2)设第个生产周期生产并销售完设备的数量为件,且y与x满足关系式.
当时,工厂第几个生产周期获得的利润最大 最大的利润是多少万元
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.
【答案】(1),;
(2),;.
【分析】()用待定系数法求出,的值即可;
()当,根据利润(售价成本)设备的数量,可得出关于的二次函数,由函数的性质求出最值;
当时,关于的函数解析式,再画出关于的函数图象的简图,由题意可得结论.
【详解】(1)把时,;时,代入得:
,解得:,;
(2)设第个生产周期创造的利润为万元,由()知,当时,,
∴,
,
,
∵,,
∴当时,取得最大值,最大值为,
∴工厂第个生产周期获得的利润最大,最大的利润是万元;
当时,,
∴,
∴,
则与的函数图象如图所示:
由图象可知,若有且只有个生产周期的利润不小于万元,
∴当,时,,
当,时,,
∴的取值范围.
【点睛】此题考查了一次函数与二次函数在销售问题中的应用,明确一次函数与二次函数的性质并分类讨论是解题的关键.
考点04 投球问题
1.(2025·贵州·中考真题)用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点,运动路径近似为抛物线,且,石块在水面上弹起后第二次与水面接触于点,运动路径近似为抛物线,且.(小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
(1)如图②,当时,若点坐标为,求抛物线的表达式;
(2)在(1)的条件下,若,在水面上有一个截面宽,高的矩形的障碍物,点的坐标为,判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;
(3)小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中,求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)
【答案】(1)
(2)不能,理由见解析
(3)
【分析】(1)利用待定系数法求解即可;
(2)首先得到,然后求出,然后将代入求解判断即可;
(3)首先求出,然后由越小开口越大,越大开口越小,点在和之间(包括这两点)得到当抛物线顶点为点M,且经过点时,开口最大,此时a最大,当抛物线顶点为点P,且经过点时,开口最小,此时a最小,然后分别利用待定系数法求解即可.
【详解】(1)∵当时,
∵点坐标为
∴
∴
∴抛物线的表达式为;
(2)不能,理由如下:
∵,点坐标为
∴
∴
∵点的坐标为,
∴
∴将代入
∴此时石块沿抛物线运动时不能越过障碍物;
(3)∵正方形,
∴
∴如图所示,
∵抛物线开口向下
∴
∵越小开口越大,越大开口越小,点在和之间(包括这两点)
∴由图象可得,当抛物线顶点为点M,且经过点时,开口最大,此时a最大
∴设的表达式为
将代入得,
解得;
∴由图象可得,当抛物线顶点为点P,且经过点时,开口最小,此时a最小
∴设的表达式为
将代入得,
解得;
∴的取值范围为.
【点睛】此题考查了二次函数的应用,待定系数法求二次函数解析式,正方形的性质等知识,数形结合是解题的关键.
2.(2025·江苏连云港·中考真题)如图,小亮同学掷铅球时,铅球沿抛物线运行,其中是铅球离初始位置的水平距离,是铅球离地面的高度.若铅球抛出时离地面的高度为,则铅球掷出的水平距离为 .
【答案】
【分析】本题考查待定系数法求抛物线解析式,二次函数与轴的交点坐标,熟练掌握待定系数法和二次函数与一元二次方程的关系是解题的关键.由题得,代入,得出抛物线的解析式为,令,求解即可,
【详解】解:由题意,,
得,
将代入,
得:,
解得:,
∴,
令,得,
解得:,,
∴为,
故答案为:.
3.(2024·甘肃兰州·中考真题)在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:
水平距离 0 3 4 10 15 20 22 27
竖直高度 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据上表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.
【答案】(1)抛物线的表达式
(2)水火箭距离地面的竖直高度米
【分析】本题主要考查二次函数的性质,
根据题意可设抛物线的表达式,结合体图标可知抛物线的顶点坐标为,代入求解即可;
由题意知,代入抛物线的表达式即可求得水火箭距离地面的竖直高度.
【详解】(1)解:根据题意可知抛物线过原点,设抛物线的表达式,
由表格得抛物线的顶点坐标为,则,解得,
则抛物线的表达式,
(2)解:由题意知,则,
那么,水火箭距离地面的竖直高度米.
4.(2024·青海·中考真题)在如图所示的平面直角坐标系中,有一斜坡,从点O处抛出一个小球,落到点处.小球在空中所经过的路线是抛物线的一部分.
(1)求抛物线的解析式;
(2)求抛物线最高点的坐标;
(3)斜坡上点B处有一棵树,点B是的三等分点,小球恰好越过树的顶端C,求这棵树的高度.
【答案】(1)
(2)
(3)这棵树的高为2
【分析】本题考查了二次函数的应用,其中涉及到待定系数法求二次函数的解析式,二次函数顶点坐标的求解方法,相似三角形的判定和性质,难度适中利用数形结合与方程思想是解题的关键.
(1)利用待定系数法求解即可;
(2)配成顶点式,利用二次函数的性质即可求解;
(3)过点A、B分别作x轴的垂线,证明,利用相似三角形的性质求得,,据此求解即可.
【详解】(1)解:∵点是抛物线上的一点,
把点代入中,得:,
解得,
∴抛物线的解析式为;
(2)解:由(1)得:,
∴抛物线最高点对坐标为;
(3)解:过点A、B分别作x轴的垂线,垂足分别是点E、D,
∵,,
∴,
∴,
又∵点B是的三等分点,
∴,
∵,
∴,,
∴,
解得,
∴,
解得,
∴点C的横坐标为1,
将代入中,,
∴点C的坐标为,
∴,
∴,
答:这棵树的高为2.
5.(2024·天津·中考真题)从地面竖直向上抛出一小球,小球的高度(单位:)与小球的运动时间(单位:)之间的关系式是.有下列结论:
①小球从抛出到落地需要;
②小球运动中的高度可以是;
③小球运动时的高度小于运动时的高度.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
【答案】C
【分析】本题考查二次函数的图像和性质,令解方程即可判断①;配方成顶点式即可判断②;把和代入计算即可判断③.
【详解】解:令,则,解得:,,
∴小球从抛出到落地需要,故①正确;
∵,
∴最大高度为,
∴小球运动中的高度可以是,故②正确;
当时,;当时,;
∴小球运动时的高度大于运动时的高度,故③错误;
故选C.
6.(2024·江西·中考真题)如图,一小球从斜坡O点以一定的方向弹出球的飞行路线可以用二次函数刻画,斜坡可以用一次函数刻画,小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如下表:
x 0 1 2 m 4 5 6 7 …
y 0 6 8 n …
(1)①______,______;
②小球的落点是A,求点A的坐标.
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系.
①小球飞行的最大高度为______米;
②求v的值.
【答案】(1)①3,6;②;
(2)①8,②
【分析】本题主要考查二次函数的应用以及从图象和表格中获取数据,
(1)①由抛物线的顶点坐标为可建立过于a,b的二元一次方程组,求出a,b的值即可;②联立两函数解析式求解,可求出交点A的坐标;
(2)①根据第一问可知最大高度为8米;
②将小球飞行高度与飞行时间的函数关系式化简为顶点式即可求得v值.
【详解】(1)解:①根据小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律表可知:抛物线顶点坐标为,
∴,
解得:,
∴二次函数解析式为,
当时,,
解得:或(舍去),
∴,
当时,,
故答案为:3,6.
②联立得:,
解得:或 ,
∴点A的坐标是,
(2)①由题干可知小球飞行最大高度为8米,
故答案为:8;
②,
则,
解得(负值舍去).
7.(2023·浙江·中考真题)根据以下素材,探究完成任务.
如何把实心球掷得更远?
素材1
小林在练习投掷实心球,其示意图如图,第一次练习时,球从点A处被抛出,其路线是抛物线.点A距离地面,当球到OA的水平距离为时,达到最大高度为.
素材2
根据体育老师建议,第二次练习时,小林在正前方处(如图)架起距离地面高为的横线.球从点A处被抛出,恰好越过横线,测得投掷距离.
问题解决
任务1
计算投掷距离 建立合适的直角坐标系,求素材1中的投掷距离.
任务2
探求高度变化 求素材2和素材1中球的最大高度的变化量
任务3
提出训练建议 为了把球掷得更远,请给小林提出一条合理的训练建议.
【答案】任务一:4m;任务二:;任务三:应该尽量提高掷出点的高度、尽量提高掷出点的速度、选择适当的掷出仰角
【分析】任务一:建立直角坐标系,由题意得:抛物线的顶点坐标为,设抛物线的解析式为,过点,利用待定系数法求出解析式,当时求出x的值即可得到;
任务二:建立直角坐标系,求出任务二的抛物线解析式,得到顶点纵坐标,与任务一的纵坐标相减即可;
任务三:根据题意给出合理的建议即可.
【详解】任务一:建立如图所示的直角坐标系,
由题意得:抛物线的顶点坐标为,
设抛物线的解析式为,过点,
∴,
解得,
∴,
当时,,
得(舍去),
∴素材1中的投掷距离为4m;
(2)建立直角坐标系,如图,
设素材2中抛物线的解析式为,
由题意得,过点,
∴,
解得,
∴
∴顶点纵坐标为,
(m),
∴素材2和素材1中球的最大高度的变化量为;
任务三:应该尽量提高掷出点的高度、尽量提高掷出点的速度、选择适当的掷出仰角.
【点睛】此题考查了二次函数的实际应用,求函数解析式,求抛物线与坐标轴的距离,正确理解题意建立恰当的直角坐标系是解题的关键.
8.(2023·内蒙古赤峰·中考真题)乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
水平距离x/
竖直高度y/
(1)在平面直角坐标系中,描出表格中各组数值所对应的点,并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是__________,当乒乓球落在对面球台上时,到起始点的水平距离是__________;
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274,球网高为15.25.现在已经计算出乒乓球恰好过网的击球高度的值约为1.27.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).
【答案】(1)见解析
(2)①;;②
(3)乒乓球恰好落在对面球台边缘点B处时,击球高度的值为
【分析】(1)根据描点法画出函数图象即可求解;
(2)①根据二次函数图象的对称性求得对称轴以及顶点,根据表格数据,可得当时,;
②待定系数法求解析式即可求解;
(3)根据题意,设平移后的抛物线的解析式为,根据题意当时,,代入进行计算即可求解.
【详解】(1)解:如图所示,
(2)①观察表格数据,可知当和时,函数值相等,则对称轴为直线,顶点坐标为,
又抛物线开口向下,可得最高点时,与球台之间的距离是,
当时,,
∴乒乓球落在对面球台上时,到起始点的水平距离是;
故答案为:;.
②设抛物线解析式为,将代入得,
,
解得:,
∴抛物线解析式为;
(3)∵当时,抛物线的解析式为,
设乒乓球恰好落在对面球台边缘点B处时,击球高度的值为,则平移距离为,
∴平移后的抛物线的解析式为,
依题意,当时,,
即,
解得:.
答:乒乓球恰好落在对面球台边缘点B处时,击球高度的值为.
【点睛】本题考查了二次函数的应用,画二次函数图象,二次函数图象的平移,熟练掌握二次函数图象的性质是解题的关键.
考点05 喷水问题
1.(2025·甘肃平凉·中考真题)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是,则水流喷出的最大高度是( )
A. B. C. D.
【答案】B
【分析】本题考查了二次函数的实际应用,正确理解题意、将抛物线转化为顶点式是解题关键;
将抛物线化为顶点式即可解决问题.
【详解】解:∵,
∴当时,;
故选:B.
2.(2023·山东滨州·中考真题)如图,要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为3米,水柱落地处离池中心3米,水管长 米.
【答案】//2.25
【分析】本题考查二次函数的实际应用,根据题意建立平面直角坐标系,设二次函数顶点式,求出二次函数解析式,再求出抛物线与y轴交点坐标即可.
【详解】解:如图,建立平面直角坐标系,
设抛物线的解析式为,
将代入,得,
解得,
∴抛物线的解析式为:,
令,得,
故答案为:.
3.(2023·山东·中考真题)城建部门计划修建一条喷泉步行通道.图1是项目俯视示意图.步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池.图2是主视示意图.喷水装置的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内,当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米.为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩,防水罩的一端固定在喷水装置上的点处,另一端与路面的垂直高度为1.8米,且与喷泉水流的水平距离为0.3米.点到水池外壁的水平距离米,求步行通道的宽.(结果精确到0.1米)参考数据:
【答案】3.2米
【分析】先以点O为坐标原点,所在直线为x轴,所在直线为y轴,建立平面直角坐标系,则,,设设抛物线的解析式为,把代入,求得,即,再求出点D的坐标,即可求解.
【详解】解:如图,建立平面直角坐标系,
由题意知:,,
∵抛物线的最高点B,
∴设抛物线的解析式为,
把代入,得,
解得,
∴抛物线的解析式为,
令,则,
解得:,
∴,
∴ (米),
答:步行通道的宽的长约为3.2米.
【点睛】本题考查抛物线的实际应用.熟练掌握用待定系数法求抛物线解析式和抛物线的图象性质是解题的关键.
4.(2023·吉林长春·中考真题)年5月8日,商业首航完成——中国民商业运营国产大飞机正式起步.时分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”、是国际民航中高级别的礼仪).如图①,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图②,当两辆消防车喷水口A、B的水平距离为米时,两条水柱在物线的顶点H处相遇,此时相遇点H距地面米,喷水口A、B距地面均为4米.若两辆消防车同时后退米,两条水柱的形状及喷水口、到地面的距离均保持不变,则此时两条水柱相遇点距地面 米.
【答案】
【分析】根据题意求出原来抛物线的解析式,从而求得平移后的抛物线解析式,再令求平移后的抛物线与轴的交点即可.
【详解】解:由题意可知:
、、,
设抛物线解析式为:,
将代入解析式,
解得:,
,
消防车同时后退米,即抛物线向左(右)平移米,
平移后的抛物线解析式为:,
令,解得:,
故答案为:.
【点睛】本题考查了待定系数法求抛物线解析式、函数图像的平移及坐标轴的交点;解题的关键是求得移动前后抛物线的解析式.
同课章节目录
