6.1.2 点、线、面、体 同步练习(含答案)
文档属性
| 名称 | 6.1.2 点、线、面、体 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 393.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览

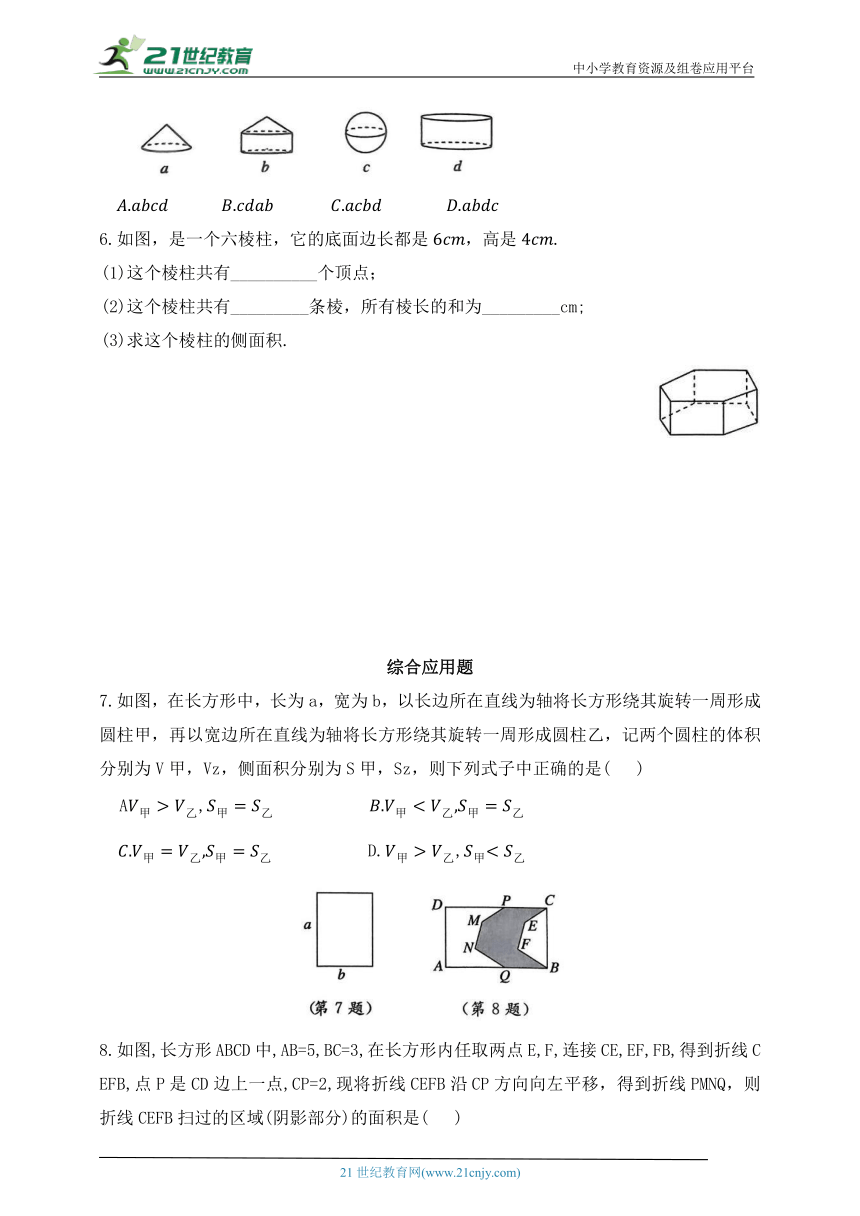
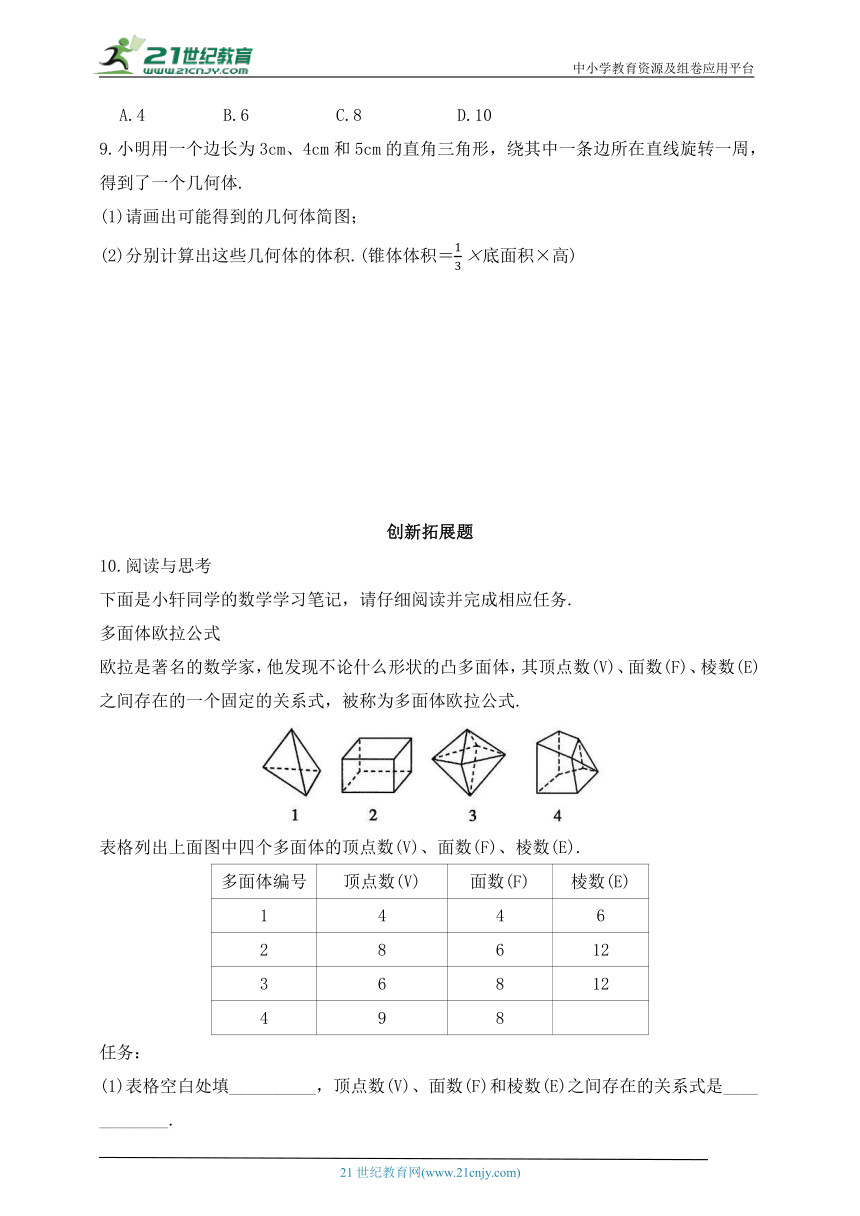
文档简介
中小学教育资源及组卷应用平台
第六章 几何图形初步
6.1 几何图形
6.1.2 点、线、面、体
基础提优题
1.如图的几何体中,含有曲面的是( )
A.①② B.①③ C.②③ D.②④
2.几何体是由曲面或平面围成的,下列几何体中面数最少的是( )
3.中华武术是中国传统文化之一,是独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
4.如图,尉迟恭单鞭救主图罐是南宁博物馆的镇馆之宝,下列平面图形绕轴旋转一周能形成这个瓷罐形状的是( )
5.如图,用纸片和小棒做成下面的小旗,快速旋转小棒,所形成的几何体的正确顺序是( )
6.如图,是一个六棱柱,它的底面边长都是,高是.
(1)这个棱柱共有__________个顶点;
(2)这个棱柱共有_________条棱,所有棱长的和为_________cm;
(3)求这个棱柱的侧面积.
综合应用题
7.如图,在长方形中,长为a,宽为b,以长边所在直线为轴将长方形绕其旋转一周形成圆柱甲,再以宽边所在直线为轴将长方形绕其旋转一周形成圆柱乙,记两个圆柱的体积分别为V甲,Vz,侧面积分别为S甲,Sz,则下列式子中正确的是( )
A,
D.,
8.如图,长方形ABCD中,AB=5,BC=3,在长方形内任取两点E,F,连接CE,EF,FB,得到折线CEFB,点P是CD边上一点,CP=2,现将折线CEFB沿CP方向向左平移,得到折线PMNQ,则折线CEFB扫过的区域(阴影部分)的面积是( )
A.4 B.6 C.8 D.10
9.小明用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边所在直线旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体简图;
(2)分别计算出这些几何体的体积.(锥体体积=底面积×高)
创新拓展题
10.阅读与思考
下面是小轩同学的数学学习笔记,请仔细阅读并完成相应任务.
多面体欧拉公式
欧拉是著名的数学家,他发现不论什么形状的凸多面体,其顶点数(V)、面数(F)、棱数(E)之间存在的一个固定的关系式,被称为多面体欧拉公式.
表格列出上面图中四个多面体的顶点数(V)、面数(F)、棱数(E).
多面体编号 顶点数(V) 面数(F) 棱数(E)
1 4 4 6
2 8 6 12
3 6 8 12
4 9 8
任务:
(1)表格空白处填__________,顶点数(V)、面数(F)和棱数(E)之间存在的关系式是____________.
(2)某个简单的多面体,是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱33条.若该多面体三角形的个数比八边形的个数的2倍少2,求该多面体三角形的个数.
(3)小轩同学尝试切去正方体一块后(用平面截取),得不到有7条棱的多面体.如果能切出有7条棱的多面体,最少需切去几块,如果不能切出有7条棱的多面体,请说明理由.
(4)如图,是由60个C原子构成的分子,它的结构为简单多面体形状.这个多面体有60个顶点,以每个顶点为一端点都有三条棱,面的形状只有五边形和六边形.按照结构,数学家构造出顶点数为n的多面体,称为“Cn”多面体,探究发现,当“Cn”多面体的面数增多时,“Cn”多面体的六边形面数也会增多,你能解释其中的道理吗
参考答案
1.D 2.C 3.A 4.C 5.B
6.【解】(1)12 (2)18;96
(3)因为侧面积等于底面周长乘高,所以6×6×4=144(cm ),所以这个棱柱的侧面积是144cm .
7.B【点拨】由题意得
因为,所以a bπ,即
而S甲=2πb·a=2abπ,S乙=2πa·b=2abπ,所以故选B.
8.B
9.【解】(1)以4cm边所在直线为轴,所得几何体简图如图①,以3cm边所在直线为轴,所得几何体简图如图②,以5cm边所在直线为轴,所得几何体简图如图③.
(2)图①的体积为图②的体积为图③的体积为
10.【解】(1)15;
(2)设八边形的个数x个,则三角形的个数为(2x-2)个,因为每个顶点处都有3条棱,共有棱33条,一条棱有两个顶点,所以所以V=22,所以F=E+2-V=33+2-22=13,所以x+(2x-2)=13,解得x=5,所以2x-2=2×5-2=8,所以该多面体三角形的个数为8个.
(3)不能切出有7条棱的多面体.理由如下:因为V+F-E=2,若E=7,则V+F=9.因为V≥4,F≥4,且V,F,E都是正整数,当V=4时,F=5,不存在这样的多面体;当V=5时,F=4,不存在这样的多面体;所以不能切出有7条棱的多面体.
(4)设顶点数为n,
因为每个顶点处都有3条棱,一条棱有两个顶点,所以
所以
设六边形的个数为a个,则五边形的个数为个,
所以解得a=因为随着n的增大而增大,所以当多面体的面数增多时,六边形的面数也会增多.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 几何图形初步
6.1 几何图形
6.1.2 点、线、面、体
基础提优题
1.如图的几何体中,含有曲面的是( )
A.①② B.①③ C.②③ D.②④
2.几何体是由曲面或平面围成的,下列几何体中面数最少的是( )
3.中华武术是中国传统文化之一,是独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面 B.线动成面,面动成体
C.点动成线,面动成体 D.点动成面,面动成线
4.如图,尉迟恭单鞭救主图罐是南宁博物馆的镇馆之宝,下列平面图形绕轴旋转一周能形成这个瓷罐形状的是( )
5.如图,用纸片和小棒做成下面的小旗,快速旋转小棒,所形成的几何体的正确顺序是( )
6.如图,是一个六棱柱,它的底面边长都是,高是.
(1)这个棱柱共有__________个顶点;
(2)这个棱柱共有_________条棱,所有棱长的和为_________cm;
(3)求这个棱柱的侧面积.
综合应用题
7.如图,在长方形中,长为a,宽为b,以长边所在直线为轴将长方形绕其旋转一周形成圆柱甲,再以宽边所在直线为轴将长方形绕其旋转一周形成圆柱乙,记两个圆柱的体积分别为V甲,Vz,侧面积分别为S甲,Sz,则下列式子中正确的是( )
A,
D.,
8.如图,长方形ABCD中,AB=5,BC=3,在长方形内任取两点E,F,连接CE,EF,FB,得到折线CEFB,点P是CD边上一点,CP=2,现将折线CEFB沿CP方向向左平移,得到折线PMNQ,则折线CEFB扫过的区域(阴影部分)的面积是( )
A.4 B.6 C.8 D.10
9.小明用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边所在直线旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体简图;
(2)分别计算出这些几何体的体积.(锥体体积=底面积×高)
创新拓展题
10.阅读与思考
下面是小轩同学的数学学习笔记,请仔细阅读并完成相应任务.
多面体欧拉公式
欧拉是著名的数学家,他发现不论什么形状的凸多面体,其顶点数(V)、面数(F)、棱数(E)之间存在的一个固定的关系式,被称为多面体欧拉公式.
表格列出上面图中四个多面体的顶点数(V)、面数(F)、棱数(E).
多面体编号 顶点数(V) 面数(F) 棱数(E)
1 4 4 6
2 8 6 12
3 6 8 12
4 9 8
任务:
(1)表格空白处填__________,顶点数(V)、面数(F)和棱数(E)之间存在的关系式是____________.
(2)某个简单的多面体,是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱33条.若该多面体三角形的个数比八边形的个数的2倍少2,求该多面体三角形的个数.
(3)小轩同学尝试切去正方体一块后(用平面截取),得不到有7条棱的多面体.如果能切出有7条棱的多面体,最少需切去几块,如果不能切出有7条棱的多面体,请说明理由.
(4)如图,是由60个C原子构成的分子,它的结构为简单多面体形状.这个多面体有60个顶点,以每个顶点为一端点都有三条棱,面的形状只有五边形和六边形.按照结构,数学家构造出顶点数为n的多面体,称为“Cn”多面体,探究发现,当“Cn”多面体的面数增多时,“Cn”多面体的六边形面数也会增多,你能解释其中的道理吗
参考答案
1.D 2.C 3.A 4.C 5.B
6.【解】(1)12 (2)18;96
(3)因为侧面积等于底面周长乘高,所以6×6×4=144(cm ),所以这个棱柱的侧面积是144cm .
7.B【点拨】由题意得
因为,所以a bπ,即
而S甲=2πb·a=2abπ,S乙=2πa·b=2abπ,所以故选B.
8.B
9.【解】(1)以4cm边所在直线为轴,所得几何体简图如图①,以3cm边所在直线为轴,所得几何体简图如图②,以5cm边所在直线为轴,所得几何体简图如图③.
(2)图①的体积为图②的体积为图③的体积为
10.【解】(1)15;
(2)设八边形的个数x个,则三角形的个数为(2x-2)个,因为每个顶点处都有3条棱,共有棱33条,一条棱有两个顶点,所以所以V=22,所以F=E+2-V=33+2-22=13,所以x+(2x-2)=13,解得x=5,所以2x-2=2×5-2=8,所以该多面体三角形的个数为8个.
(3)不能切出有7条棱的多面体.理由如下:因为V+F-E=2,若E=7,则V+F=9.因为V≥4,F≥4,且V,F,E都是正整数,当V=4时,F=5,不存在这样的多面体;当V=5时,F=4,不存在这样的多面体;所以不能切出有7条棱的多面体.
(4)设顶点数为n,
因为每个顶点处都有3条棱,一条棱有两个顶点,所以
所以
设六边形的个数为a个,则五边形的个数为个,
所以解得a=因为随着n的增大而增大,所以当多面体的面数增多时,六边形的面数也会增多.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
