6.3.2 角的比较与运算 第1课时 角的比较与运算 同步练习(含答案)
文档属性
| 名称 | 6.3.2 角的比较与运算 第1课时 角的比较与运算 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 几何图形初步
6.3.2 角的比较与运算
第1课时 角的比较与运算
基础提优题
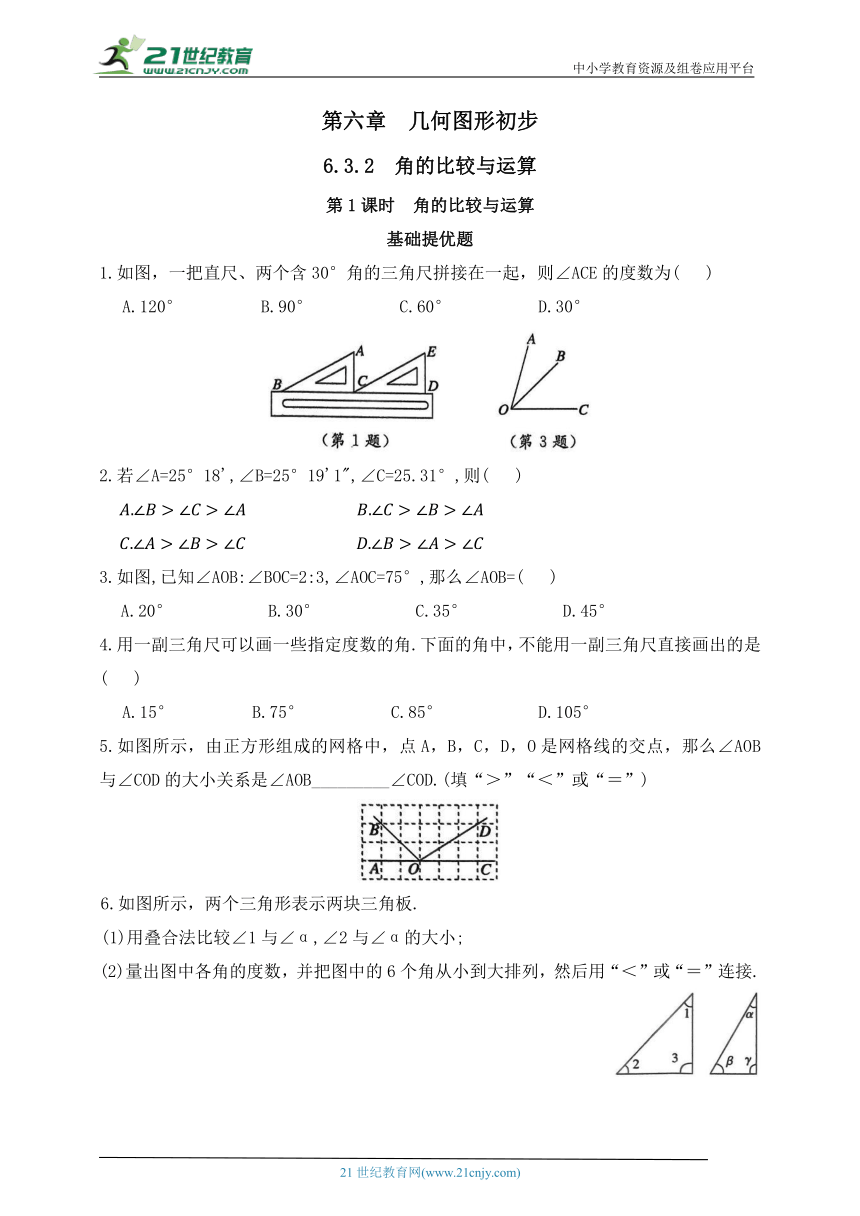
1.如图,一把直尺、两个含30°角的三角尺拼接在一起,则∠ACE的度数为( )
A.120° B.90° C.60° D.30°
2.若∠A=25°18',∠B=25°19'1",∠C=25.31°,则( )
3.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20° B.30° C.35° D.45°
4.用一副三角尺可以画一些指定度数的角.下面的角中,不能用一副三角尺直接画出的是( )
A.15° B.75° C.85° D.105°
5.如图所示,由正方形组成的网格中,点A,B,C,D,O是网格线的交点,那么∠AOB与∠COD的大小关系是∠AOB_________∠COD.(填“>”“<”或“=”)
6.如图所示,两个三角形表示两块三角板.
(1)用叠合法比较∠1与∠α,∠2与∠α的大小;
(2)量出图中各角的度数,并把图中的6个角从小到大排列,然后用“<”或“=”连接.
7.计算:
(1)153°29′42"+26°40′32"; (2)42°15′÷5;
(3)62°24′17"×4; (4)180°-(34°54′+21°33′).
综合应用题
8.如图,点A表示养心殿所在位置,点O表示太和殿所在位置,点B表示文渊阁所在位置.已知养心殿位于太和殿北偏西21°18′方向上,文渊阁位于太和殿南偏东58°18′方向上,则∠AOB的度数是( )
A.78°36′ B.143° C.140° D.153°
9.如图,已知∠AOB=180°,∠AOC=110°,现将射线OA绕点O顺时针匀速旋转,射线OB,OC保持不动,当射线OA与射线OB重合时停止旋转.当三条射线构成的角中有两个角相等(重合除外)时,射线OA旋转的角度为_____________.
10.如图,将三个同样的直角三角尺的直角顶点重合放置,那么∠AOB的度数为____________.
11.如图,已知∠AOE=130°.∠AOB:∠BOC=2:1,且3∠COE=2∠AOB.求∠AOB的度数.
12.日常生活中,我们几乎每天都要看钟表,它的时针和分针如同兄弟俩在赛跑,其中蕴涵着丰富的数学知识.
(1)如图①,上午8:00这一时刻,钟表上分针与时针的夹角等于_________.
(2)请在图②中画出8:20这一时刻时针和分针的大致位置,思考并回答:从上午8:00到8:20,钟表的分针转过的度数是_________,钟表的时针转过的度数是__________.
(3)“元旦”这一天,小明上午8:00出门买东西,回到家中时发现还没到,但是时针与分针重合了,那么小明从离开家到回到家的时间为多少分钟
创新拓展题
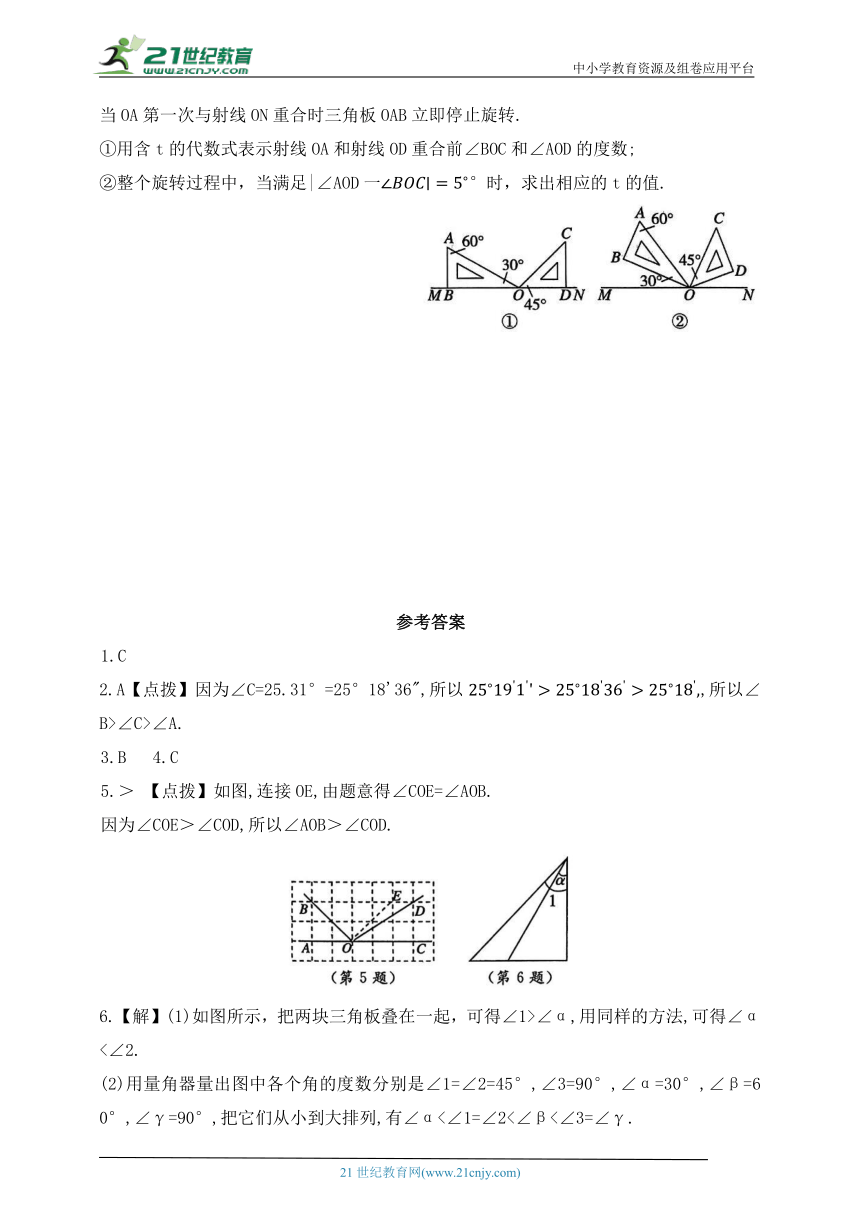
13.如图①,将两块直角三角板(一块含有30°、60°角,另一块含45°角)摆放在直线MN上,三角板ODC绕点O以每秒15°的速度逆时针旋转.当OD第一次与射线OM重合时三角板ODC停止旋转,设旋转时间为ts.
(1)当t=2时,求∠BOC和∠AOD的度数.
(2)如图②,若两块三角板同时旋转,三角板OAB以每秒20°的速度绕点O顺时针旋转,当OA第一次与射线ON重合时三角板OAB立即停止旋转.
①用含t的代数式表示射线OA和射线OD重合前∠BOC和∠AOD的度数;
②整个旋转过程中,当满足|∠AOD一°时,求出相应的t的值.
参考答案
1.C
2.A【点拨】因为∠C=25.31°=25°18'36",所以,所以∠B>∠C>∠A.
3.B 4.C
5.> 【点拨】如图,连接OE,由题意得∠COE=∠AOB.
因为∠COE>∠COD,所以∠AOB>∠COD.
6.【解】(1)如图所示,把两块三角板叠在一起,可得∠1>∠α,用同样的方法,可得∠α<∠2.
(2)用量角器量出图中各个角的度数分别是∠1=∠2=45°,∠3=90°,∠α=30°,∠β=60°,∠γ=90°,把它们从小到大排列,有∠α<∠1=∠2<∠β<∠3=∠γ.
7.【解】(1)153°29′42"+26°40′32"=179°69′74"=180°10′14".
507′=8°27′.
(3)62°24′17"×4=248°96′68"=249°37′8"。
(4)180°-(34°54′+21°33′)=180°-56°27′=123°33′.
8.B
9.40°或145°【点拨】三条射线构成的角中有两个角相等(重合除外)时,可能存在以下两种情形:①当射线OA旋转到∠BOC的外部时,∠AOC=∠BOC.
因为,∠AOC=110°,所以∠BOC=70°.所以∠AOC=70°.
所以射线OA旋转的角度为110°-70°=40°.
②当射线OA旋转到∠BOC内部时,∠AOC=∠AOB.所以
所以射线OA旋转的角度为180°-35°=145°.
综上,射线OA旋转的角度为40°或145°.
10.20°【点拨】如图.
易知∠COE=90°,∠AOC=90°-∠COD=90°-30°=60°,∠EOB=90°-∠EOF=90°-40°=50°,所以∠AOB=∠AOC+∠BOE-∠COE=60°+50°-90°=20°.
11.【解】因为∠AOB:∠BOC=2:1,所以设∠BOC=x,则∠AOB=2x.
因为3∠COE=2∠AOB,所以
因为∠AOE=∠AOB+∠BOC+∠COE=130°,所以解得x=30°,
所以∠AOB=2x=60°.
12.【解】(1)120°
(2)如图.120°;10°
【点拨】因为分针每分钟转6°,时针每分钟转0.5°,所以上午8:00到8:20分针转过的度数为120°,时针转过的度数为10°.
(3)设小明从离开家到回到家的时间为x(x<60)分钟.由题意易得分针比时针多走了240°,所以6x-0.5x=240,解得.
所以小明从离开家到回到家的时间为分钟.
点方法 钟面角是常见的一种角的问题,求钟面角首先要清楚时针和分针每分钟转过的度数,其次时针与分针的问题很多时候类似于追及问题.本题中时针与分针重合其实就是分针追上了时针,所以分针比时针多走了240°
13.【解】(1)由题图①,得∠BOC=180°-45°=135°,∠AOD=180°-30°=150°.当t=2时,三角板ODC绕点O逆时针旋转,∠BOC与∠AOD减小的度数相同,
为15°×2=30°,故∠BOC=135°-30°=105°,∠AOD=150°-30°=120°.
(2)①由题意,得∠AOM=(30+20t)°,∠NOD=(15t)°,
令20t+15t+45=180,解得令30+20t+15t=180,解得
所以射线OB与射线OC重合之前
射线OA与射线OD重合之前
所以∠AOD=180°-(∠AOM+∠NOD)=(150-35t)°.
当0<t<时,∠BOC=(135-35t)°;当时,∠BOC=(35t-135)°.
②由题意知,OA运动时间为150°÷20°=7.5(s).
OD运动时间为180°÷15°=12(s).
当0<时,∠AOD=(150-35t)°,∠BOC=(135-35t)°,
此时,∠AOD-∠BOC=(150-35t)°-(135—35t)°=15°,不符合题意;
当时,∠AOD=(150-35t)°,∠BOC=(35t-135)°,
令,解得t=4或;
当时.∠AOD=∠MOA-∠MOD=(30+20t)°-(180-15t)°=(35t-150)°,∠BOC=∠BOM-∠MOC=(20t)°-(135-15t)°=(35t-135)°或∠BOC=∠BOM+∠MOC=(20t)°+(15t-135)°=(35t-135)°,此时,不符合题意;
当7.5<t<12时,OA停止运动.当OC未过BO延长线时,∠AOD=(15t)°,
∠BOC=∠BOD+∠DOC=(15t-30)°+45°=(15t+15)°,
此时,不符合题意,
当OC已过BO延长线时,∠AOD=(15t)°,∠BOC=360°-(15t+15)°=(345-15t)°,令,解得或
综上,t=4或2或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 几何图形初步
6.3.2 角的比较与运算
第1课时 角的比较与运算
基础提优题
1.如图,一把直尺、两个含30°角的三角尺拼接在一起,则∠ACE的度数为( )
A.120° B.90° C.60° D.30°
2.若∠A=25°18',∠B=25°19'1",∠C=25.31°,则( )
3.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20° B.30° C.35° D.45°
4.用一副三角尺可以画一些指定度数的角.下面的角中,不能用一副三角尺直接画出的是( )
A.15° B.75° C.85° D.105°
5.如图所示,由正方形组成的网格中,点A,B,C,D,O是网格线的交点,那么∠AOB与∠COD的大小关系是∠AOB_________∠COD.(填“>”“<”或“=”)
6.如图所示,两个三角形表示两块三角板.
(1)用叠合法比较∠1与∠α,∠2与∠α的大小;
(2)量出图中各角的度数,并把图中的6个角从小到大排列,然后用“<”或“=”连接.
7.计算:
(1)153°29′42"+26°40′32"; (2)42°15′÷5;
(3)62°24′17"×4; (4)180°-(34°54′+21°33′).
综合应用题
8.如图,点A表示养心殿所在位置,点O表示太和殿所在位置,点B表示文渊阁所在位置.已知养心殿位于太和殿北偏西21°18′方向上,文渊阁位于太和殿南偏东58°18′方向上,则∠AOB的度数是( )
A.78°36′ B.143° C.140° D.153°
9.如图,已知∠AOB=180°,∠AOC=110°,现将射线OA绕点O顺时针匀速旋转,射线OB,OC保持不动,当射线OA与射线OB重合时停止旋转.当三条射线构成的角中有两个角相等(重合除外)时,射线OA旋转的角度为_____________.
10.如图,将三个同样的直角三角尺的直角顶点重合放置,那么∠AOB的度数为____________.
11.如图,已知∠AOE=130°.∠AOB:∠BOC=2:1,且3∠COE=2∠AOB.求∠AOB的度数.
12.日常生活中,我们几乎每天都要看钟表,它的时针和分针如同兄弟俩在赛跑,其中蕴涵着丰富的数学知识.
(1)如图①,上午8:00这一时刻,钟表上分针与时针的夹角等于_________.
(2)请在图②中画出8:20这一时刻时针和分针的大致位置,思考并回答:从上午8:00到8:20,钟表的分针转过的度数是_________,钟表的时针转过的度数是__________.
(3)“元旦”这一天,小明上午8:00出门买东西,回到家中时发现还没到,但是时针与分针重合了,那么小明从离开家到回到家的时间为多少分钟
创新拓展题
13.如图①,将两块直角三角板(一块含有30°、60°角,另一块含45°角)摆放在直线MN上,三角板ODC绕点O以每秒15°的速度逆时针旋转.当OD第一次与射线OM重合时三角板ODC停止旋转,设旋转时间为ts.
(1)当t=2时,求∠BOC和∠AOD的度数.
(2)如图②,若两块三角板同时旋转,三角板OAB以每秒20°的速度绕点O顺时针旋转,当OA第一次与射线ON重合时三角板OAB立即停止旋转.
①用含t的代数式表示射线OA和射线OD重合前∠BOC和∠AOD的度数;
②整个旋转过程中,当满足|∠AOD一°时,求出相应的t的值.
参考答案
1.C
2.A【点拨】因为∠C=25.31°=25°18'36",所以,所以∠B>∠C>∠A.
3.B 4.C
5.> 【点拨】如图,连接OE,由题意得∠COE=∠AOB.
因为∠COE>∠COD,所以∠AOB>∠COD.
6.【解】(1)如图所示,把两块三角板叠在一起,可得∠1>∠α,用同样的方法,可得∠α<∠2.
(2)用量角器量出图中各个角的度数分别是∠1=∠2=45°,∠3=90°,∠α=30°,∠β=60°,∠γ=90°,把它们从小到大排列,有∠α<∠1=∠2<∠β<∠3=∠γ.
7.【解】(1)153°29′42"+26°40′32"=179°69′74"=180°10′14".
507′=8°27′.
(3)62°24′17"×4=248°96′68"=249°37′8"。
(4)180°-(34°54′+21°33′)=180°-56°27′=123°33′.
8.B
9.40°或145°【点拨】三条射线构成的角中有两个角相等(重合除外)时,可能存在以下两种情形:①当射线OA旋转到∠BOC的外部时,∠AOC=∠BOC.
因为,∠AOC=110°,所以∠BOC=70°.所以∠AOC=70°.
所以射线OA旋转的角度为110°-70°=40°.
②当射线OA旋转到∠BOC内部时,∠AOC=∠AOB.所以
所以射线OA旋转的角度为180°-35°=145°.
综上,射线OA旋转的角度为40°或145°.
10.20°【点拨】如图.
易知∠COE=90°,∠AOC=90°-∠COD=90°-30°=60°,∠EOB=90°-∠EOF=90°-40°=50°,所以∠AOB=∠AOC+∠BOE-∠COE=60°+50°-90°=20°.
11.【解】因为∠AOB:∠BOC=2:1,所以设∠BOC=x,则∠AOB=2x.
因为3∠COE=2∠AOB,所以
因为∠AOE=∠AOB+∠BOC+∠COE=130°,所以解得x=30°,
所以∠AOB=2x=60°.
12.【解】(1)120°
(2)如图.120°;10°
【点拨】因为分针每分钟转6°,时针每分钟转0.5°,所以上午8:00到8:20分针转过的度数为120°,时针转过的度数为10°.
(3)设小明从离开家到回到家的时间为x(x<60)分钟.由题意易得分针比时针多走了240°,所以6x-0.5x=240,解得.
所以小明从离开家到回到家的时间为分钟.
点方法 钟面角是常见的一种角的问题,求钟面角首先要清楚时针和分针每分钟转过的度数,其次时针与分针的问题很多时候类似于追及问题.本题中时针与分针重合其实就是分针追上了时针,所以分针比时针多走了240°
13.【解】(1)由题图①,得∠BOC=180°-45°=135°,∠AOD=180°-30°=150°.当t=2时,三角板ODC绕点O逆时针旋转,∠BOC与∠AOD减小的度数相同,
为15°×2=30°,故∠BOC=135°-30°=105°,∠AOD=150°-30°=120°.
(2)①由题意,得∠AOM=(30+20t)°,∠NOD=(15t)°,
令20t+15t+45=180,解得令30+20t+15t=180,解得
所以射线OB与射线OC重合之前
射线OA与射线OD重合之前
所以∠AOD=180°-(∠AOM+∠NOD)=(150-35t)°.
当0<t<时,∠BOC=(135-35t)°;当时,∠BOC=(35t-135)°.
②由题意知,OA运动时间为150°÷20°=7.5(s).
OD运动时间为180°÷15°=12(s).
当0<时,∠AOD=(150-35t)°,∠BOC=(135-35t)°,
此时,∠AOD-∠BOC=(150-35t)°-(135—35t)°=15°,不符合题意;
当时,∠AOD=(150-35t)°,∠BOC=(35t-135)°,
令,解得t=4或;
当时.∠AOD=∠MOA-∠MOD=(30+20t)°-(180-15t)°=(35t-150)°,∠BOC=∠BOM-∠MOC=(20t)°-(135-15t)°=(35t-135)°或∠BOC=∠BOM+∠MOC=(20t)°+(15t-135)°=(35t-135)°,此时,不符合题意;
当7.5<t<12时,OA停止运动.当OC未过BO延长线时,∠AOD=(15t)°,
∠BOC=∠BOD+∠DOC=(15t-30)°+45°=(15t+15)°,
此时,不符合题意,
当OC已过BO延长线时,∠AOD=(15t)°,∠BOC=360°-(15t+15)°=(345-15t)°,令,解得或
综上,t=4或2或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
