6.3.2 角的比较与运算 第2课时 角平分线 同步练习(含答案)
文档属性
| 名称 | 6.3.2 角的比较与运算 第2课时 角平分线 同步练习(含答案) | 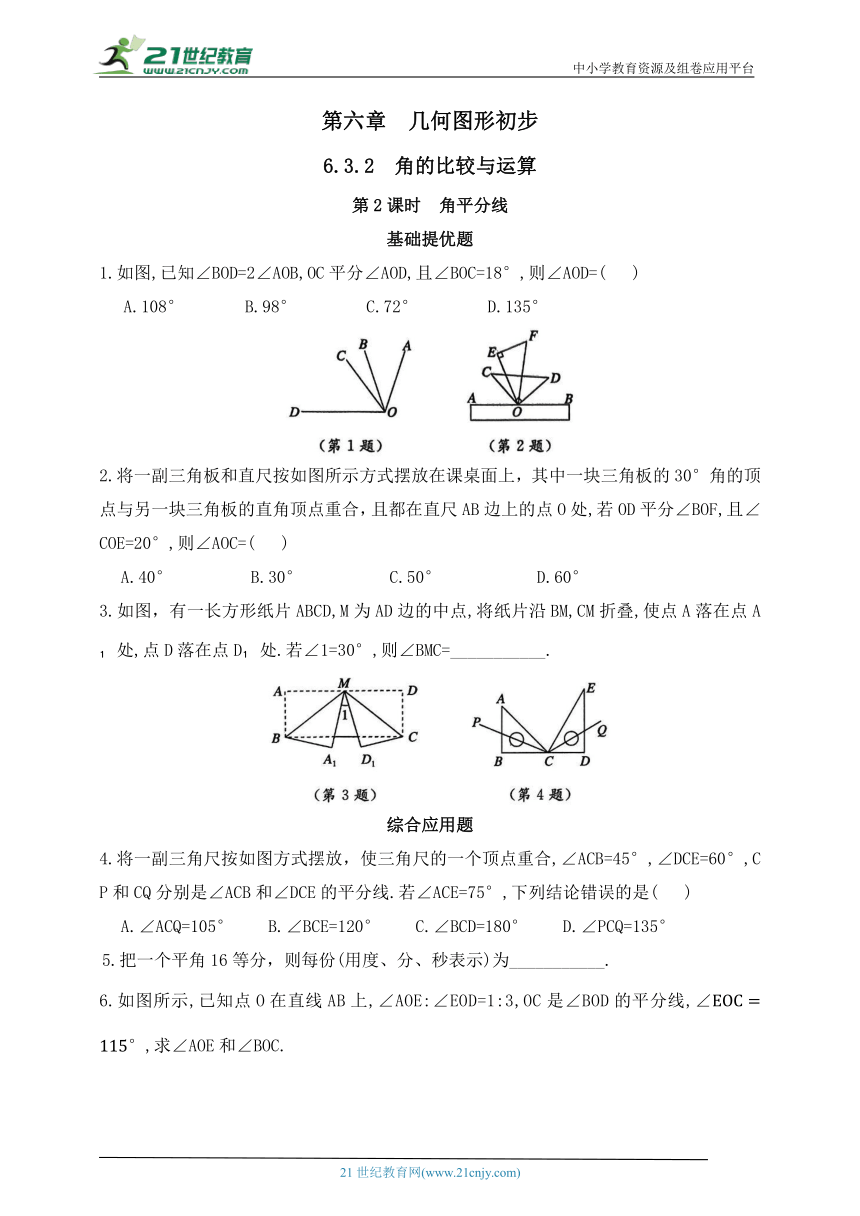 | |
| 格式 | docx | ||
| 文件大小 | 328.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 15:03:44 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 几何图形初步
6.3.2 角的比较与运算
第2课时 角平分线
基础提优题
1.如图,已知∠BOD=2∠AOB,OC平分∠AOD,且∠BOC=18°,则∠AOD=( )
A.108° B.98° C.72° D.135°
2.将一副三角板和直尺按如图所示方式摆放在课桌面上,其中一块三角板的30°角的顶点与另一块三角板的直角顶点重合,且都在直尺AB边上的点O处,若OD平分∠BOF,且∠COE=20°,则∠AOC=( )
A.40° B.30° C.50° D.60°
3.如图,有一长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A 处,点D落在点D 处.若∠1=30°,则∠BMC=___________.
综合应用题
4.将一副三角尺按如图方式摆放,使三角尺的一个顶点重合,∠ACB=45°,∠DCE=60°,CP和CQ分别是∠ACB和∠DCE的平分线.若∠ACE=75°,下列结论错误的是( )
A.∠ACQ=105° B.∠BCE=120° C.∠BCD=180° D.∠PCQ=135°
5.把一个平角16等分,则每份(用度、分、秒表示)为___________.
6.如图所示,已知点O在直线AB上,∠AOE:∠EOD=1:3,OC是∠BOD的平分线,,求∠AOE和∠BOC.
创新拓展题
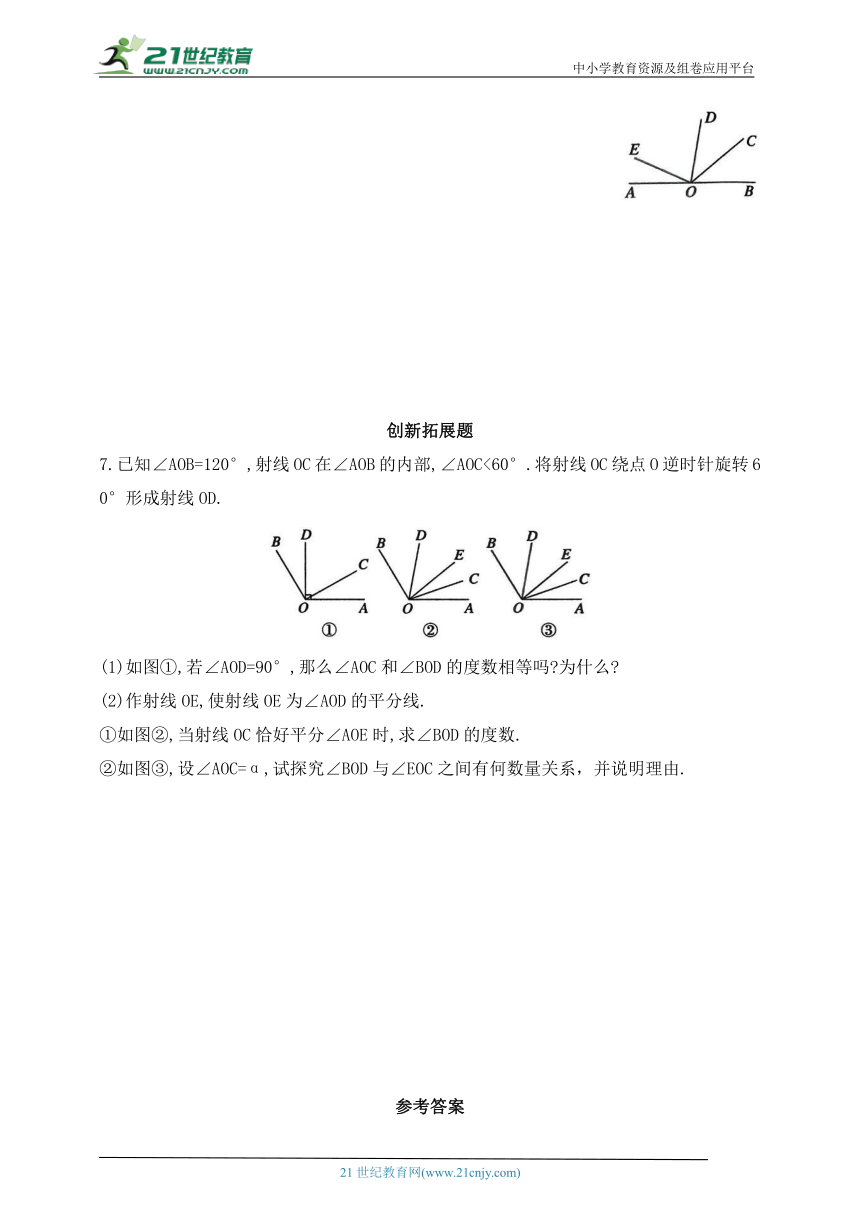
7.已知∠AOB=120°,射线OC在∠AOB的内部,∠AOC<60°.将射线OC绕点O逆时针旋转60°形成射线OD.
(1)如图①,若∠AOD=90°,那么∠AOC和∠BOD的度数相等吗 为什么
(2)作射线OE,使射线OE为∠AOD的平分线.
①如图②,当射线OC恰好平分∠AOE时,求∠BOD的度数.
②如图③,设∠AOC=α,试探究∠BOD与∠EOC之间有何数量关系,并说明理由.
参考答案
1.A【点拨】设∠AOD=6x,因为∠BOD=2∠AOB,所以∠BOD=4x,∠AOB=2x.
因为OC平分∠AOD,所以∠AOC=∠DOC=3x.
由题意得3x-2x=18°,解得x=18°,所以∠AOD=6x=108°,故选A.
2.C【点拨】由题意得∠COD=90°,∠EOF=30°.
因为∠COE=20°,所以∠DOF=∠COD-∠COE-∠EOF=90°-30°-20°=40°.
因为OD平分∠BOF,所以∠DOF=∠DOB=40°,
所以∠AOC=180°-∠COD-∠DOB=180°-90°-40°=50°.
3.105°【点拨】因为∠1=30°,所以∠AMA +
因为将纸片沿BM,CM折叠,使点A落在点A 处,点D落在点D 处,
所以MB平分∠AMA ,MC平分∠DMD ,
所以
所以
所以∠BMC=∠1+∠BMA +
4.D【点拨】因为∠ACB=45°,∠DCE=60°,CP和CQ分别是∠ACB和∠DCE的平分线,所以22.5°.
因为∠ACE=75°,所以∠ACQ=∠ACE+∠ECQ=75°+30°=105°,∠BCE=∠BCA+∠ACE=45°+75°=120°,∠BCD=∠BCA+∠ACE+∠ECD=45°+75°+60°=180°,∠PCQ=∠PCA+∠ACE+∠ECQ=22.5°+75°+30°=127.5°≠135°.
5.11°15′【点拨】180°÷16=11.25°.
因为0.25°=(0.25×60)'=15',,所以11.25°=11°15′,故答案为11°15′.
6.【解】因为∠AOE:∠EOD=1:3,所以设∠AOE=x,则∠EOD=3x.
又因为∠EOC=115°,所以∠COD=115°-3x.
因为OC是∠BOD的平分线,所以∠COB=∠COD=115°-3x.
因为点O在直线AB上,所以∠AOE+∠EOD+∠COD+∠COB=180°,
所以x+3x+2(115°-3x)=180°,解得x=25°,
所以∠AOE=25°,∠BOC=115°-3×25°=40°.
7.【解】(1)∠AOC和∠BOD的度数相等.理由如下:
因为∠AOB=120°,∠AOD=90°,所以∠BOD=120°-90°=30°.
由题可知∠COD=60°,所以∠AOC=90°-60°=30°.
所以∠AOC=∠BOD=30°.
(2)①因为射线OC恰好平分∠AOE,所以∠AOC=∠COE.
因为射线OE平分∠AOD,所以∠DOE=∠AOE=∠AOC+∠COE=2∠AOC.
因为∠COD=60°,所以∠DOE+∠COE=60°,所以2∠AOC+∠AOC=60°,
所以∠AOC=20°,所以∠COE=20°,∠DOE=40°.
因为∠AOB=120°,所以
②数量关系是∠BOD=2∠EOC.理由如下:
因为∠COD=60°,∠AOC=α,所以∠AOD=60°+α.
因为射线OE平分∠AOD,所以
所以
因为∠AOB=120°,所以∠BOD=120°-∠AOD=120°-(60°+α)=60°-α.
所以∠BOD=2∠EOC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 几何图形初步
6.3.2 角的比较与运算
第2课时 角平分线
基础提优题
1.如图,已知∠BOD=2∠AOB,OC平分∠AOD,且∠BOC=18°,则∠AOD=( )
A.108° B.98° C.72° D.135°
2.将一副三角板和直尺按如图所示方式摆放在课桌面上,其中一块三角板的30°角的顶点与另一块三角板的直角顶点重合,且都在直尺AB边上的点O处,若OD平分∠BOF,且∠COE=20°,则∠AOC=( )
A.40° B.30° C.50° D.60°
3.如图,有一长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A 处,点D落在点D 处.若∠1=30°,则∠BMC=___________.
综合应用题
4.将一副三角尺按如图方式摆放,使三角尺的一个顶点重合,∠ACB=45°,∠DCE=60°,CP和CQ分别是∠ACB和∠DCE的平分线.若∠ACE=75°,下列结论错误的是( )
A.∠ACQ=105° B.∠BCE=120° C.∠BCD=180° D.∠PCQ=135°
5.把一个平角16等分,则每份(用度、分、秒表示)为___________.
6.如图所示,已知点O在直线AB上,∠AOE:∠EOD=1:3,OC是∠BOD的平分线,,求∠AOE和∠BOC.
创新拓展题
7.已知∠AOB=120°,射线OC在∠AOB的内部,∠AOC<60°.将射线OC绕点O逆时针旋转60°形成射线OD.
(1)如图①,若∠AOD=90°,那么∠AOC和∠BOD的度数相等吗 为什么
(2)作射线OE,使射线OE为∠AOD的平分线.
①如图②,当射线OC恰好平分∠AOE时,求∠BOD的度数.
②如图③,设∠AOC=α,试探究∠BOD与∠EOC之间有何数量关系,并说明理由.
参考答案
1.A【点拨】设∠AOD=6x,因为∠BOD=2∠AOB,所以∠BOD=4x,∠AOB=2x.
因为OC平分∠AOD,所以∠AOC=∠DOC=3x.
由题意得3x-2x=18°,解得x=18°,所以∠AOD=6x=108°,故选A.
2.C【点拨】由题意得∠COD=90°,∠EOF=30°.
因为∠COE=20°,所以∠DOF=∠COD-∠COE-∠EOF=90°-30°-20°=40°.
因为OD平分∠BOF,所以∠DOF=∠DOB=40°,
所以∠AOC=180°-∠COD-∠DOB=180°-90°-40°=50°.
3.105°【点拨】因为∠1=30°,所以∠AMA +
因为将纸片沿BM,CM折叠,使点A落在点A 处,点D落在点D 处,
所以MB平分∠AMA ,MC平分∠DMD ,
所以
所以
所以∠BMC=∠1+∠BMA +
4.D【点拨】因为∠ACB=45°,∠DCE=60°,CP和CQ分别是∠ACB和∠DCE的平分线,所以22.5°.
因为∠ACE=75°,所以∠ACQ=∠ACE+∠ECQ=75°+30°=105°,∠BCE=∠BCA+∠ACE=45°+75°=120°,∠BCD=∠BCA+∠ACE+∠ECD=45°+75°+60°=180°,∠PCQ=∠PCA+∠ACE+∠ECQ=22.5°+75°+30°=127.5°≠135°.
5.11°15′【点拨】180°÷16=11.25°.
因为0.25°=(0.25×60)'=15',,所以11.25°=11°15′,故答案为11°15′.
6.【解】因为∠AOE:∠EOD=1:3,所以设∠AOE=x,则∠EOD=3x.
又因为∠EOC=115°,所以∠COD=115°-3x.
因为OC是∠BOD的平分线,所以∠COB=∠COD=115°-3x.
因为点O在直线AB上,所以∠AOE+∠EOD+∠COD+∠COB=180°,
所以x+3x+2(115°-3x)=180°,解得x=25°,
所以∠AOE=25°,∠BOC=115°-3×25°=40°.
7.【解】(1)∠AOC和∠BOD的度数相等.理由如下:
因为∠AOB=120°,∠AOD=90°,所以∠BOD=120°-90°=30°.
由题可知∠COD=60°,所以∠AOC=90°-60°=30°.
所以∠AOC=∠BOD=30°.
(2)①因为射线OC恰好平分∠AOE,所以∠AOC=∠COE.
因为射线OE平分∠AOD,所以∠DOE=∠AOE=∠AOC+∠COE=2∠AOC.
因为∠COD=60°,所以∠DOE+∠COE=60°,所以2∠AOC+∠AOC=60°,
所以∠AOC=20°,所以∠COE=20°,∠DOE=40°.
因为∠AOB=120°,所以
②数量关系是∠BOD=2∠EOC.理由如下:
因为∠COD=60°,∠AOC=α,所以∠AOD=60°+α.
因为射线OE平分∠AOD,所以
所以
因为∠AOB=120°,所以∠BOD=120°-∠AOD=120°-(60°+α)=60°-α.
所以∠BOD=2∠EOC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
