第六章 几何图形初步 阶段性测试题 角的认识及计算(含答案)
文档属性
| 名称 | 第六章 几何图形初步 阶段性测试题 角的认识及计算(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 15:05:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 几何图形初步
阶段性测试题 角的认识及计算
[时间:45分钟 分值:100分]
一、选择题(每题4分,共32分)
1.下列说法错误的是( )
A.角是由两条有公共端点的射线组成的图形
B.周角的一半叫平角
C.14°42′可转化为14.7°
D.直线MN是平角
2.下列图形中,能用∠O和∠1表示同一个角的是( )
3.如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC的大小为( )
A.36° B.44° C.54° D.63°
4.如图,点A,B,O分别表示手绘地图中厦门鼓浪屿风景区内郑成功纪念馆、郑成功水操台遗址、日光岩三个景点.经测量∠AOB=66°,郑成功水操台遗址在日光岩的北偏东28°方向,则郑成功纪念馆在日光岩的( )
A.北偏东38°方向 B.北偏西28°方向
C.北偏西38°方向 D.北偏东52°方向
5.用一副三角板不能画出的角是( )
A.75° B.105° C.110° D.135°
6.“铃铃铃”上课铃声响了,小明一看时间是下午2时30分,如果一节课是45分钟,那么下课时分针和时针的夹角是( )
A.15° B.7.5° C.5° D.0°
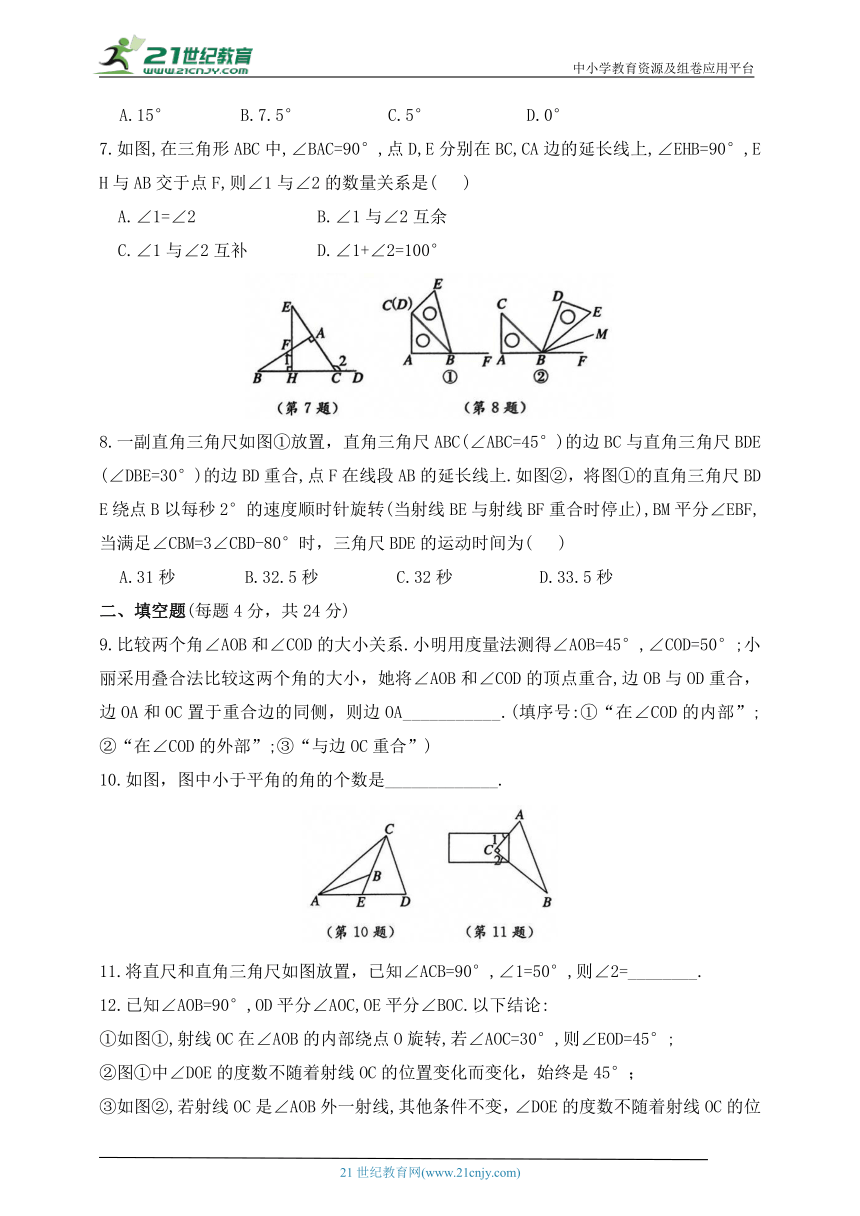
7.如图,在三角形ABC中,∠BAC=90°,点D,E分别在BC,CA边的延长线上,∠EHB=90°,EH与AB交于点F,则∠1与∠2的数量关系是( )
A.∠1=∠2 B.∠1与∠2互余
C.∠1与∠2互补 D.∠1+∠2=100°
8.一副直角三角尺如图①放置,直角三角尺ABC(∠ABC=45°)的边BC与直角三角尺BDE(∠DBE=30°)的边BD重合,点F在线段AB的延长线上.如图②,将图①的直角三角尺BDE绕点B以每秒2°的速度顺时针旋转(当射线BE与射线BF重合时停止),BM平分∠EBF,当满足∠CBM=3∠CBD-80°时,三角尺BDE的运动时间为( )
A.31秒 B.32.5秒 C.32秒 D.33.5秒
二、填空题(每题4分,共24分)
9.比较两个角∠AOB和∠COD的大小关系.小明用度量法测得∠AOB=45°,∠COD=50°;小丽采用叠合法比较这两个角的大小,她将∠AOB和∠COD的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA___________.(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)
10.如图,图中小于平角的角的个数是_____________.
11.将直尺和直角三角尺如图放置,已知∠ACB=90°,∠1=50°,则∠2=________.
12.已知∠AOB=90°,OD平分∠AOC,OE平分∠BOC.以下结论:
①如图①,射线OC在∠AOB的内部绕点O旋转,若∠AOC=30°,则∠EOD=45°;
②图①中∠DOE的度数不随着射线OC的位置变化而变化,始终是45°;
③如图②,若射线OC是∠AOB外一射线,其他条件不变,∠DOE的度数不随着射线OC的位置变化而变化,始终是45°.
正确的是_________________(只填写序号).
13.在我国古代,人们用“铜壶滴漏”的方法计时,把一昼夜分为十二时辰,对应今天的二十四小时,又划为九十六刻,一刻对应今天的十五分钟.已知寅时为凌晨三点到五点.则寅时二刻所对应钟表时间的时针和分针之间所夹的角度为____________.
14.如图,将长方形纸片的一角折叠,使顶点A落在A′处,DE为折痕.将对折,使得落在直线上,得折痕EG,若恰好平分∠DEB,则∠DEG=,
三、解答题(共44分)
15.(12分)计算:
(精确到分)
16.(14分)如图,直线AB,CD相交于点O,OE平分∠BOC,∠DOF=90°.
(1)若∠AOF=50°,则∠BOE的度数为______________;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
17.(18分)点O在直线AD上,在直线AD的同侧作射线OB,OC,OM,且OM平分
(1)如图①,若∠AOB=40°,∠COD=60°,则∠BOC的度数为__________,∠BOM的度数为____________;
(2)如图②,若求∠BOC的度数;
(3)若∠AOC和∠AOB互为余角且∠AOC≠30°,45°,60°,ON平分∠BOD,试画出图形探究∠BOM与∠CON之间的数量关系,并说明理由.
参考答案
一、1.D 2.A 3.C 4.C 5.C
6.B【点拨】由题意得下课时间为3时15分,所以下课时分针和时针的夹角是
7.C【点拨】易知∠1+∠B=90°,∠ECH+∠B=90°,所以∠1=∠ECH.
又因为∠2+∠ECH=180°,所以∠1+∠2=180°,即∠1与∠2互补,故选C.
8.B【点拨】设三角尺BDE的运动时间为t秒,由题意得∠CBD=(2t)°.
因为,所以
因为BM平分∠EBF,所以
因为∠CBM=3∠CBD-80°,所以180-45-(52.5-t)=6t-80,解得t=32.5.
所以三角尺BDE的运动时间为32.5秒.
二、9.① 10.11 11.40°
12.①②③【点拨】①因为∠AOC=30°,∠AOB=90°,所以因为OD平分∠AOC,OE平分∠BOC,所以∠COE=所以∠EOD=∠EOC+∠COD=45°.故①正确;②如题图①,因为OD平分∠AOC,所以∠DOC=因为OE平分∠BOC,所以∠COE=因为∠DOE=∠DOC+∠COE,所以因为∠AOB=90°,所以故②正确;③如题图②,因为OD平分∠AOC,所以因为OE平分∠BOC,所以因为∠DOE=∠COE-∠DOC,所以因为∠AOB=90°,所以∠DOE=故③正确.
13.75°【点拨】寅时二刻是指3:30,此时时针在钟面3和4的中间,分针正对着6,即时针和分针为2.5个大格,所以寅时二刻所对应钟表时间的时针和分针之间所夹的角度为30°×2.5=75°.
14.90°;30°【点拨】由折叠得,所以易得∠DEG=90°.因为平分∠DEB,所以,所以.因为180°,所以∠DEA=60°.易知∠A=90°,所以∠ADE=30°,所以易知∠ADC=90°,所以.
三、15.【解】(1)180°÷7≈25°43′.
16.【解】(1)70°【点拨】因为∠DOF=90°,所以∠COF=180°-∠DOF=90°.因为∠AOF=50°,所以∠AOC=90°-∠AOF=90°-50°=40°.所以∠BOC=180°-∠AOC=180°-40°=140°.因为OE平分∠BOC,所以∠BOE=
(2)因为∠BOD:∠BOE=1:4,所以设∠BOD=x,则∠BOE=4x.
因为OE平分∠BOC,所以∠BOC=2∠BOE=8x.
因为∠BOD+∠BOC=180°,所以x+8x=180°,解得x=20°.所以∠BOD=20°.
易得∠AOF+∠BOD=90°,所以∠AOF=90°-∠BOD=90°-20°=70°.
17.【解】(1)80°;20°
(2)设∠BOM=x.
因为所以∠COD=2x.所以∠AOC=180°-2x.
因为OM平分∠AOC,所以
所以∠BOC=∠BOM+∠COM=90°.
(3)∠BOM+∠CON=45°或∠CON-∠BOM=45°.
理由:如图①,
设∠AOB=α,则∠BOD=180°-∠AOB=180°-α.
因为∠AOC和∠AOB互为余角,所以∠AOC=90°-α.
因为OM平分∠AOC,所以
所以
因为ON平分∠BOD,所以
所以
所以∠BOM+∠CON=45°.
如图②,设∠AOB=β,则∠AOC=90°-β.
同理可得所以∠CON-∠BOM=45°.
综上所述,∠BOM与∠CON之间的数量关系为∠BOM+∠CON=45°或∠CON-∠BOM=45°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 几何图形初步
阶段性测试题 角的认识及计算
[时间:45分钟 分值:100分]
一、选择题(每题4分,共32分)
1.下列说法错误的是( )
A.角是由两条有公共端点的射线组成的图形
B.周角的一半叫平角
C.14°42′可转化为14.7°
D.直线MN是平角
2.下列图形中,能用∠O和∠1表示同一个角的是( )
3.如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC的大小为( )
A.36° B.44° C.54° D.63°
4.如图,点A,B,O分别表示手绘地图中厦门鼓浪屿风景区内郑成功纪念馆、郑成功水操台遗址、日光岩三个景点.经测量∠AOB=66°,郑成功水操台遗址在日光岩的北偏东28°方向,则郑成功纪念馆在日光岩的( )
A.北偏东38°方向 B.北偏西28°方向
C.北偏西38°方向 D.北偏东52°方向
5.用一副三角板不能画出的角是( )
A.75° B.105° C.110° D.135°
6.“铃铃铃”上课铃声响了,小明一看时间是下午2时30分,如果一节课是45分钟,那么下课时分针和时针的夹角是( )
A.15° B.7.5° C.5° D.0°
7.如图,在三角形ABC中,∠BAC=90°,点D,E分别在BC,CA边的延长线上,∠EHB=90°,EH与AB交于点F,则∠1与∠2的数量关系是( )
A.∠1=∠2 B.∠1与∠2互余
C.∠1与∠2互补 D.∠1+∠2=100°
8.一副直角三角尺如图①放置,直角三角尺ABC(∠ABC=45°)的边BC与直角三角尺BDE(∠DBE=30°)的边BD重合,点F在线段AB的延长线上.如图②,将图①的直角三角尺BDE绕点B以每秒2°的速度顺时针旋转(当射线BE与射线BF重合时停止),BM平分∠EBF,当满足∠CBM=3∠CBD-80°时,三角尺BDE的运动时间为( )
A.31秒 B.32.5秒 C.32秒 D.33.5秒
二、填空题(每题4分,共24分)
9.比较两个角∠AOB和∠COD的大小关系.小明用度量法测得∠AOB=45°,∠COD=50°;小丽采用叠合法比较这两个角的大小,她将∠AOB和∠COD的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA___________.(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)
10.如图,图中小于平角的角的个数是_____________.
11.将直尺和直角三角尺如图放置,已知∠ACB=90°,∠1=50°,则∠2=________.
12.已知∠AOB=90°,OD平分∠AOC,OE平分∠BOC.以下结论:
①如图①,射线OC在∠AOB的内部绕点O旋转,若∠AOC=30°,则∠EOD=45°;
②图①中∠DOE的度数不随着射线OC的位置变化而变化,始终是45°;
③如图②,若射线OC是∠AOB外一射线,其他条件不变,∠DOE的度数不随着射线OC的位置变化而变化,始终是45°.
正确的是_________________(只填写序号).
13.在我国古代,人们用“铜壶滴漏”的方法计时,把一昼夜分为十二时辰,对应今天的二十四小时,又划为九十六刻,一刻对应今天的十五分钟.已知寅时为凌晨三点到五点.则寅时二刻所对应钟表时间的时针和分针之间所夹的角度为____________.
14.如图,将长方形纸片的一角折叠,使顶点A落在A′处,DE为折痕.将对折,使得落在直线上,得折痕EG,若恰好平分∠DEB,则∠DEG=,
三、解答题(共44分)
15.(12分)计算:
(精确到分)
16.(14分)如图,直线AB,CD相交于点O,OE平分∠BOC,∠DOF=90°.
(1)若∠AOF=50°,则∠BOE的度数为______________;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
17.(18分)点O在直线AD上,在直线AD的同侧作射线OB,OC,OM,且OM平分
(1)如图①,若∠AOB=40°,∠COD=60°,则∠BOC的度数为__________,∠BOM的度数为____________;
(2)如图②,若求∠BOC的度数;
(3)若∠AOC和∠AOB互为余角且∠AOC≠30°,45°,60°,ON平分∠BOD,试画出图形探究∠BOM与∠CON之间的数量关系,并说明理由.
参考答案
一、1.D 2.A 3.C 4.C 5.C
6.B【点拨】由题意得下课时间为3时15分,所以下课时分针和时针的夹角是
7.C【点拨】易知∠1+∠B=90°,∠ECH+∠B=90°,所以∠1=∠ECH.
又因为∠2+∠ECH=180°,所以∠1+∠2=180°,即∠1与∠2互补,故选C.
8.B【点拨】设三角尺BDE的运动时间为t秒,由题意得∠CBD=(2t)°.
因为,所以
因为BM平分∠EBF,所以
因为∠CBM=3∠CBD-80°,所以180-45-(52.5-t)=6t-80,解得t=32.5.
所以三角尺BDE的运动时间为32.5秒.
二、9.① 10.11 11.40°
12.①②③【点拨】①因为∠AOC=30°,∠AOB=90°,所以因为OD平分∠AOC,OE平分∠BOC,所以∠COE=所以∠EOD=∠EOC+∠COD=45°.故①正确;②如题图①,因为OD平分∠AOC,所以∠DOC=因为OE平分∠BOC,所以∠COE=因为∠DOE=∠DOC+∠COE,所以因为∠AOB=90°,所以故②正确;③如题图②,因为OD平分∠AOC,所以因为OE平分∠BOC,所以因为∠DOE=∠COE-∠DOC,所以因为∠AOB=90°,所以∠DOE=故③正确.
13.75°【点拨】寅时二刻是指3:30,此时时针在钟面3和4的中间,分针正对着6,即时针和分针为2.5个大格,所以寅时二刻所对应钟表时间的时针和分针之间所夹的角度为30°×2.5=75°.
14.90°;30°【点拨】由折叠得,所以易得∠DEG=90°.因为平分∠DEB,所以,所以.因为180°,所以∠DEA=60°.易知∠A=90°,所以∠ADE=30°,所以易知∠ADC=90°,所以.
三、15.【解】(1)180°÷7≈25°43′.
16.【解】(1)70°【点拨】因为∠DOF=90°,所以∠COF=180°-∠DOF=90°.因为∠AOF=50°,所以∠AOC=90°-∠AOF=90°-50°=40°.所以∠BOC=180°-∠AOC=180°-40°=140°.因为OE平分∠BOC,所以∠BOE=
(2)因为∠BOD:∠BOE=1:4,所以设∠BOD=x,则∠BOE=4x.
因为OE平分∠BOC,所以∠BOC=2∠BOE=8x.
因为∠BOD+∠BOC=180°,所以x+8x=180°,解得x=20°.所以∠BOD=20°.
易得∠AOF+∠BOD=90°,所以∠AOF=90°-∠BOD=90°-20°=70°.
17.【解】(1)80°;20°
(2)设∠BOM=x.
因为所以∠COD=2x.所以∠AOC=180°-2x.
因为OM平分∠AOC,所以
所以∠BOC=∠BOM+∠COM=90°.
(3)∠BOM+∠CON=45°或∠CON-∠BOM=45°.
理由:如图①,
设∠AOB=α,则∠BOD=180°-∠AOB=180°-α.
因为∠AOC和∠AOB互为余角,所以∠AOC=90°-α.
因为OM平分∠AOC,所以
所以
因为ON平分∠BOD,所以
所以
所以∠BOM+∠CON=45°.
如图②,设∠AOB=β,则∠AOC=90°-β.
同理可得所以∠CON-∠BOM=45°.
综上所述,∠BOM与∠CON之间的数量关系为∠BOM+∠CON=45°或∠CON-∠BOM=45°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
