第六章 几何图形初步 专题 几何图形初步认识的常见题型(含答案)
文档属性
| 名称 | 第六章 几何图形初步 专题 几何图形初步认识的常见题型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 358.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 15:09:10 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 几何图形初步
专题 几何图形初步认识的常见题型
题型1 利用物体的特征构建几何体模型
1.在粉笔盒、三棱镜、乒乓球、易拉罐瓶、书本、热水瓶胆中,形状类似于棱柱的有__________个.
题型2 利用生活中的情境构建平面几何模型
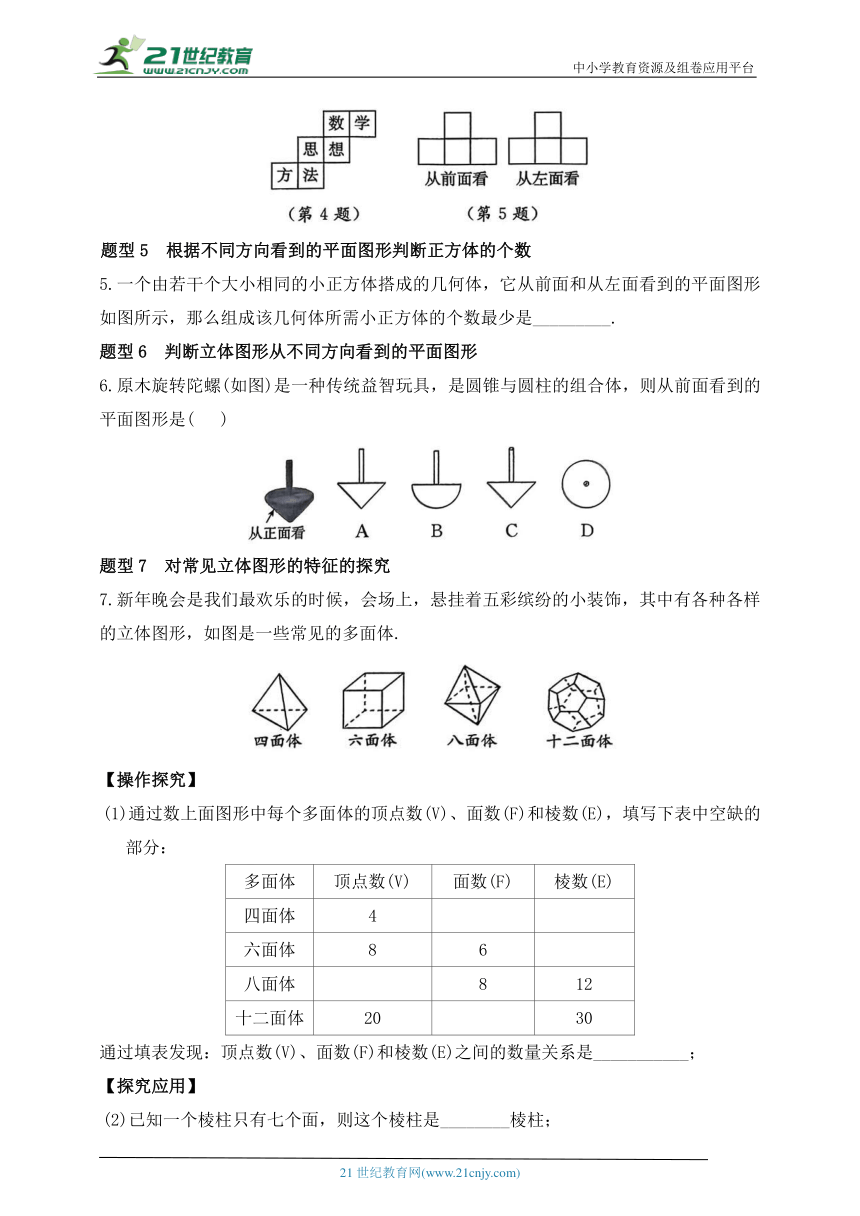
2.如图,这是一座房子的平面图,它的组成有( )
A.三角形、长方形 B.三角形、正方形、长方形
C.三角形、正方形、长方形、梯形 D.正方形、长方形、梯形
题型3 利用常见立体图形的特征进行分类
3.如图(a),请帮助甲、乙、丙三名同学从图(b)中选出合适的立体图形.
题型4 利用图形的展开与折叠辨识相对面
4.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“数”字的一面相对面上的字是__________.
题型5 根据不同方向看到的平面图形判断正方体的个数
5.一个由若干个大小相同的小正方体搭成的几何体,它从前面和从左面看到的平面图形如图所示,那么组成该几何体所需小正方体的个数最少是_________.
题型6 判断立体图形从不同方向看到的平面图形
6.原木旋转陀螺(如图)是一种传统益智玩具,是圆锥与圆柱的组合体,则从前面看到的平面图形是( )
题型7 对常见立体图形的特征的探究
7.新年晚会是我们最欢乐的时候,会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形,如图是一些常见的多面体.
【操作探究】
(1)通过数上面图形中每个多面体的顶点数(V)、面数(F)和棱数(E),填写下表中空缺的部分:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4
六面体 8 6
八面体 8 12
十二面体 20 30
通过填表发现:顶点数(V)、面数(F)和棱数(E)之间的数量关系是___________;
【探究应用】
(2)已知一个棱柱只有七个面,则这个棱柱是________棱柱;
(3)已知一个多面体只有8个顶点,并且过每个顶点都有3条棱,求这个多面体的面数.
参考答案
1.3 2.C
3.【解】甲选②和④;乙选①;丙选①和③.
4.法
5.4【点拨】由该几何体从前面和从左面看到的平面图形可确定所需小正方体个数最少时从上面看到的平面图形如图(数字表示小正方体的个数),则组成该几何体所需小正方体的个数最少是1+2+1=4(个).
6.A
7.【解】(1)填表如下:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
六面体 8 6 12
八面体 6 8 12
十二面体 20 12 30
(2)五
(3)由题意得棱的总条数为(条).
由,可得,解得.故这个多面体的面数为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 几何图形初步
专题 几何图形初步认识的常见题型
题型1 利用物体的特征构建几何体模型
1.在粉笔盒、三棱镜、乒乓球、易拉罐瓶、书本、热水瓶胆中,形状类似于棱柱的有__________个.
题型2 利用生活中的情境构建平面几何模型
2.如图,这是一座房子的平面图,它的组成有( )
A.三角形、长方形 B.三角形、正方形、长方形
C.三角形、正方形、长方形、梯形 D.正方形、长方形、梯形
题型3 利用常见立体图形的特征进行分类
3.如图(a),请帮助甲、乙、丙三名同学从图(b)中选出合适的立体图形.
题型4 利用图形的展开与折叠辨识相对面
4.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“数”字的一面相对面上的字是__________.
题型5 根据不同方向看到的平面图形判断正方体的个数
5.一个由若干个大小相同的小正方体搭成的几何体,它从前面和从左面看到的平面图形如图所示,那么组成该几何体所需小正方体的个数最少是_________.
题型6 判断立体图形从不同方向看到的平面图形
6.原木旋转陀螺(如图)是一种传统益智玩具,是圆锥与圆柱的组合体,则从前面看到的平面图形是( )
题型7 对常见立体图形的特征的探究
7.新年晚会是我们最欢乐的时候,会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形,如图是一些常见的多面体.
【操作探究】
(1)通过数上面图形中每个多面体的顶点数(V)、面数(F)和棱数(E),填写下表中空缺的部分:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4
六面体 8 6
八面体 8 12
十二面体 20 30
通过填表发现:顶点数(V)、面数(F)和棱数(E)之间的数量关系是___________;
【探究应用】
(2)已知一个棱柱只有七个面,则这个棱柱是________棱柱;
(3)已知一个多面体只有8个顶点,并且过每个顶点都有3条棱,求这个多面体的面数.
参考答案
1.3 2.C
3.【解】甲选②和④;乙选①;丙选①和③.
4.法
5.4【点拨】由该几何体从前面和从左面看到的平面图形可确定所需小正方体个数最少时从上面看到的平面图形如图(数字表示小正方体的个数),则组成该几何体所需小正方体的个数最少是1+2+1=4(个).
6.A
7.【解】(1)填表如下:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
六面体 8 6 12
八面体 6 8 12
十二面体 20 12 30
(2)五
(3)由题意得棱的总条数为(条).
由,可得,解得.故这个多面体的面数为6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
