2025年新八年级数学人教版暑假大讲堂第十讲 全等三角形判定二(含解析)
文档属性
| 名称 | 2025年新八年级数学人教版暑假大讲堂第十讲 全等三角形判定二(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 09:15:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年新八年级数学人教版暑假大讲堂
第十讲 全等三角形判定二
知识点梳理
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
要点诠释:
夹边要求:必须是两角的公共边
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
要点诠释:
当已知条件中涉及两角及非夹边时,优先使用AAS判定。例如,已知两角和其中一角的对边相等,可直接套用AAS定理
知识点3判定方法的选择
选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS
要点诠释:
如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
题型1 添加条件使能够运用ASA、AAS判定三角形全等
例1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
避免混淆 :ASA要求夹边,AAS要求非夹边;
隐含条件 :对顶角、公共边等可辅助证明;
反例说明 :AAA(三个角相等)不能判定全等
针对训练1
1.如图,在和中,点A,E,B,D在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
2.如图,D在上,E在上,且.补充下列一个条件后,仍无法判定的是( )
A. B. C. D.
3.如图,与相交于点O,,,不添加辅助线,判定的依据是( )
A. B. C. D.
4.在中,,,,下列条件能得到的是( )
A.,, B.,,
C.,, D.,,
5.如图,点B、F、C、E在一条直线上,,,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
题型2 利用ASA全等证明线段相等
例2.如图,在与中,已知,,,若,,则_________.
需准确识别夹边条件,避免混淆非对应边。
结合其他定理(如等腰三角形三线合一)可简化证明过程
针对训练2
1.如图,,,,且.
求证:.
2.如图,已知,,,.求证:.
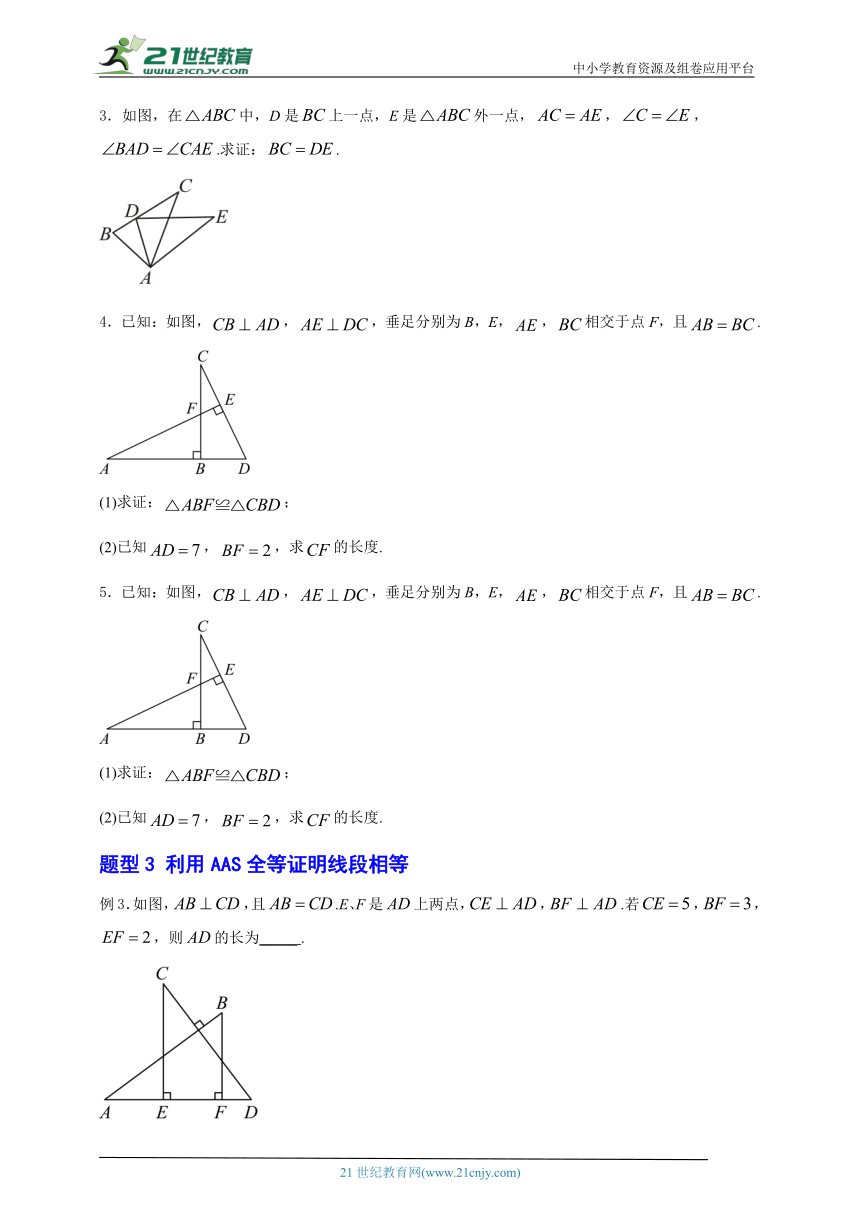
3.如图,在中,D是上一点,E是外一点,,,.求证:.
4.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
5.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
题型3 利用AAS全等证明线段相等
例3.如图,,且.E、F是上两点,,.若,,,则的长为_____ .
转化思路 :若条件中未直接给出AAS,可通过三角形内角和定理将两角及其中一角的对边转化为AAS形式。例如,已知两角及非对边相等时,可证明第三个角也相等,从而满足AAS。
辅助线添加 :在复杂图形中,适当添加辅助线(如作高、中线或延长线)构造全等三角形。例如,在直角三角形中,利用斜边中线性质辅助证明
针对训练3
1.如图,在中,,是的平分线,于E,F在上,,试证明:
(1).
(2).
2.如图,已知:,求证:
3.已知:如图,,点D是的中点,平分,,垂足为E.
求证:.
4.如图,已知在四边形中,点E在上,,,.
(1)求证:;
(2)若,,求的度数.
.
5.已知:如图,点A、B、E在同一直线上,且,,
求证:
题型4 全等三角形判定方法选择
例4.综合与探究
问题情境:在中,,,点D在直线上运动,连接,将线段绕点A顺时针旋转得到线段,过点E作,交直线于点F.
探究发现:
(1)如图1,当点D在上时,与的数量关系是__________.
(2)如图2,当点D在的延长线上时,连接交于点H.求证:.
拓展思考:
(3)当,时,直接写出的面积.
已知两边及夹角 :直接用SAS;
已知两角及一边 :用ASA或AAS;
等腰三角形 :结合SAS或ASA;
中点、角平分线 :通过构造全等三角形辅助证明
针对训练4
1.如图,的边AB与的边ED相交于点F,连接CF.已知,,.
(1)求证:;
(2)求证:FC平分.
2.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
3.如图,在中,,延长至点E,过点E作,使,连接交于点D.
(1)求证:;
(2)若G是上一点,满足,连接,证明:.
4.如图,在四边形ACBD中,点P在对角线AB上,连接,,,.
试说明:(1);
(2).
5.如图,在中,两边AB,AC上有两点M,N,D为外一点,且,,,.
(1)猜想线段MN,BM,CN之间的数量关系并说明理由.
(2)若,,求的周长.
题型5 ASA、AAS全等的实际应用
例5.小丽与爸爸、妈妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,与地面垂直,小丽两脚在地面上用力一蹬,妈妈在B处接住她后用力一堆,爸爸在C处接住她.若点B距离地面的高度为,点B到的距离为,点C距离地面的高度是,,则点C到的距离为 _____ 米.
条件识别
ASA :当已知条件中两个角及它们的夹边时直接使用。
AAS :当已知条件中两个角及其中一角的对边时使用
书写规范
用相同符号标记相等边,加粗或特殊符号突出条件顺序(如ASA需夹边在中间)。
注意区分“夹边”与“对边”,避免混淆。
证明步骤
ASA :先证明两角相等,再证明夹边相等,最后得出全等结论。
AAS :先证明两角相等,再证明其中一角的对边相等,通过三角形内角和推导出第三对角相等,最终证明全等。
针对训练5
1.咸阳宫位于渭水之北,泾水之南,是中国历史上最恢宏壮丽的宫殿之一.某数学研究小组的同学们把测量咸阳宫城墙的高度作为一项课题活动,设计了如表所示的测量方案:
课题 测量咸阳宫城墙的高度
成员 组长:×××组员:×××,×××,×××
测量工具 测角仪、皮尺等
测量示意图
测量说明 如图,,,甲同学在小树与城墙之间的点E处,分别测得、,发现α与β互余
测量数据 米,米
请你根据上述信息求出咸阳宫城墙的高度.
2.如图,小亮站在河边的点A处,在河的对面(小亮的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30米到达一棵树点C处,接着再向前走了30米到达点D处,然后他左转向南直行,当小亮看到电线塔、树与自己现处的位置E在一条直线上时,他共走了140米.
(1)根据题意,画出示意图;
(2)求小亮在点A处时他与电线塔的距离,并说明理由.
3.如图,要测量河两岸相对的两点A、B的距离,可以在的垂线上取两点C、D,使,再过点D作,使A、C、E在一条直线上,这时测得的的长就是的长,你知道其中的道理吗?请给出你的证明.
4.综合与实践
【主题】军事训练中的距离测量问题
【素材】在某次重要的军事训练任务中,士兵小王肩负着一项关键使命:精准测量我方阵地(点A)与对岸目标(点B)之间的距离.然而,摆在小王面前的是诸多棘手难题,河流湍急无法直接过河,且身处野外环境没有携带任何专业测量工具.但小王凭借着扎实的数学知识和冷静的头脑,巧妙地运用了以下方法来解决这一难题:
【实践操作】如图所示:
步骤1:面向点B站立,调整目视高度,使视线恰好经过帽檐到达点;
步骤2:保持身体姿态不变,原地转过一个角度,标记此时视线落在河岸的点C;
步骤3:步测得米.已知小王身高为,帽顶O到眼睛D的垂直距离为.
【问题解决】
(1)如何测得我方阵地与对岸目标之间的距离?请用你所学数学知识说明.
(2)若将本题中的测量方法应用到生活场景中,例如测量池塘对岸某一物体的距离,你认为该方法是否同样适用?请举例说明在生活场景应用时可能会遇到的不同情况及相应的解决办法.
5.学习《利用三角形全等测距离》后,“开拓”小组的同学就“测量河两岸A,B两点间的距离”这一问题,设计了如下方案:如图,在点B所在河岸同侧平地上取点C和点D.使点A,B,C在一条直线上,且,测得,,在CD的延长线上取一点E,使,这时测得DE的长就是A,B两点间的距离.你同意他们的说法吗?请说明理由.
创新拓展能力提升
1.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
2.如图1,已知中,,,AE是过点A的一条直线,点B,C在直线AE的两侧,于点D,于点E,.
(1)试说明:.
(2)若直线AE绕点A旋转到图2的位置,其余条件不变,则BD与DE,CE的关系如何?请说明理由.
(3)若直线AE绕点A旋转到图3的位置,其余条件不变,则BD与DE,CE的关系如何?请直接写出结果.
(4)归纳(1)(2)(3)问,请用简洁的语言表述BD,DE,CE的关系.
3.如图,在平面直角坐标系中,已知点、分别为x轴和y轴上一点,且a,b满足,过点B作于点E,延长至点D,使得,连接、,平分.
(1)A点的坐标为;的度数为.
(2)如图1,若点C在第四象限,试判断与的数量关系与位置关系,并说明理由.
(3)如图2,连接,平分,若点C的坐标为,连接交于点E,与交于点F.
①求D点的坐标;
②试判断与的数量关系,并说明理由.
2025年新八年级数学人教版暑假大讲堂
第十讲 全等三角形判定二(解析版)
知识点梳理
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
要点诠释:
夹边要求:必须是两角的公共边
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
要点诠释:
当已知条件中涉及两角及非夹边时,优先使用AAS判定。例如,已知两角和其中一角的对边相等,可直接套用AAS定理
知识点3判定方法的选择
选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS
要点诠释:
如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
题型1 添加条件使能够运用ASA、AAS判定三角形全等
例1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
避免混淆 :ASA要求夹边,AAS要求非夹边;
隐含条件 :对顶角、公共边等可辅助证明;
反例说明 :AAA(三个角相等)不能判定全等
【答案】∠A=∠D(答案不唯一).
【解析】先说明∠ACB=∠DCE,再添加∠A=∠D,再结合BC=EC运用AAS即可证明△ABC≌△DEC.
解:添加条件:∠A=∠D;
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA即∠ACB=∠DCE
在△ABC和△DEC中
∠A=∠D ,∠ACB=∠DCE,BC=EC
∴△ABC≌△DEC(AAS).
故答案为:∠A=∠D(答案不唯一).
【点睛】本题考查了全等三角形的判定定理;掌握全等三角形的判定方法是解答本题的关键.
针对训练1
1.如图,在和中,点A,E,B,D在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
答案:B
解析:因为,所以.因为,所以添加,无法判定;
添加,则,即,根据“SAS”可判定;
添加,无法判定;
添加,无法判定.
2.如图,D在上,E在上,且.补充下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:B
解析:∵,,
∴要使全等,只需要一组对应边对应相等即可,
∴当或或时,,
当时,三组对应角相等,不能判定,
故选B.
3.如图,与相交于点O,,,不添加辅助线,判定的依据是( )
A. B. C. D.
答案:B
解析:在与中,
,
∴;
故选:B.
4.在中,,,,下列条件能得到的是( )
A.,, B.,,
C.,, D.,,
答案:C
解析:∵,
∴,,,
∴,
故选C.
5.如图,点B、F、C、E在一条直线上,,,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:C
解析:选项A、添加可用AAS进行判定,故本选不符合题意;
选项B、添加可用AAS进行判定,故本选项不符合题意;
选项C、添加不能判定,故本选项符合题意;
选项D、添加可得出,然后可用ASA进行判定,故本选项不符合题意.
故选C.
题型2 利用ASA全等证明线段相等
例2.如图,在与中,已知,,,若,,则_________.
需准确识别夹边条件,避免混淆非对应边。
结合其他定理(如等腰三角形三线合一)可简化证明过程
答案:10
解析:∵,
∴,
又∵,,
∴,
∴,
∵,,
∴,
∴,
故答案为:10.
针对训练2
1.如图,,,,且.
求证:.
答案:见解析.
解析:∵,,
∴,,
∴.
又,,
∴.
∴.
2.如图,已知,,,.求证:.
答案:见解析
解析:证明:∵,
∴,
∴,
∵,,
∴,
∴.
3.如图,在中,D是上一点,E是外一点,,,.求证:.
答案:见解析
解析:∵,
则,
∴,
在和中,
,
∴,
∴.
4.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
答案:(1)见解析
(2).
解析:(1)证明:,
,
;
,
,
;
在和中,
,
;
(2),,
,,
,
,
.
5.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
答案:(1)见解析
(2).
解析:(1)证明:,
,
;
,
,
;
在和中,
,
;
(2),,
,,
,
,
.
题型3 利用AAS全等证明线段相等
例3.如图,,且.E、F是上两点,,.若,,,则的长为_____ .
转化思路 :若条件中未直接给出AAS,可通过三角形内角和定理将两角及其中一角的对边转化为AAS形式。例如,已知两角及非对边相等时,可证明第三个角也相等,从而满足AAS。
辅助线添加 :在复杂图形中,适当添加辅助线(如作高、中线或延长线)构造全等三角形。例如,在直角三角形中,利用斜边中线性质辅助证明
答案:6
解析:∵,,
∴,,
∴,
在和中,
,
∴
∴,,
∵
∴
∴
故答案是:6.
针对训练3
1.如图,在中,,是的平分线,于E,F在上,,试证明:
(1).
(2).
答案:(1)见解析
(2)见解析
解析:(1)证明:∵是的平分线,
∴,
∵,
∴,
又∵,
∴,
∴,
又∵,,
∴,
∴;
(2)证明:∵,
∴,
∵,
∴,
∵,
∴.
2.如图,已知:,求证:
答案:见解析
解析:,
∴,
即,
在和中,
,
∴,
∴.
3.已知:如图,,点D是的中点,平分,,垂足为E.
求证:.
答案:见解析
解析:∵,点D是的中点,
∴,
∴.
∵,
∴.
∵平分,
∴.
在和中,,,,
∴,
∴.
4.如图,已知在四边形中,点E在上,,,.
(1)求证:;
(2)若,,求的度数.
答案:(1)证明见解析;(2)
解析:∵,
∴,
∴,
在和中,
,
∴,
∴;
(2)∵,,
∴
∵,
∴.
5.已知:如图,点A、B、E在同一直线上,且,,
求证:
答案:见解析.
解析:
在与中
题型4 全等三角形判定方法选择
例4.综合与探究
问题情境:在中,,,点D在直线上运动,连接,将线段绕点A顺时针旋转得到线段,过点E作,交直线于点F.
探究发现:
(1)如图1,当点D在上时,与的数量关系是__________.
(2)如图2,当点D在的延长线上时,连接交于点H.求证:.
拓展思考:
(3)当,时,直接写出的面积.
已知两边及夹角 :直接用SAS;
已知两角及一边 :用ASA或AAS;
等腰三角形 :结合SAS或ASA;
中点、角平分线 :通过构造全等三角形辅助证明
答案:(1)
(2)见解析
(3)12或24
解析:∵,
∴,
又∵,
∴,
∴,
由旋转得,,
又∵,
∴,
∴,
在和中,
∴,
∴;
(2)由旋转得,,
∵,
∴,
∵,
∴,
∵,
∴,
又在中,,
∴,即,
在和中,
∴,
∴,
又,
∴,
∵,且,
∴,
又,
∴
在和中,
∴,
∴;
(3)∵,,
∴当点D在的延长线上时,,不满足题意,
∴点D在上,由(1)知,
∴,
∴,
∵,
∴.
当点D在的延长线上时,如图,
同理可得,,,
∴,
综上,的面积为12或24.
针对训练4
1.如图,的边AB与的边ED相交于点F,连接CF.已知,,.
(1)求证:;
(2)求证:FC平分.
答案:(1)见解析
(2)见解析
解析:(1)∵,
∴,
即,
在与中
,
∴,
∴;
(2)过点C作,,垂足分别为G,H,
∵,
∴,
∵,,
∴,
在与中
,
∴,
∴,
∴FC平分.
2.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析;
(2)3.
解析:,
,
即:,
在和中,
,
∴,
;
(2)解析:由(1)得,
,
,,
.
3.如图,在中,,延长至点E,过点E作,使,连接交于点D.
(1)求证:;
(2)若G是上一点,满足,连接,证明:.
答案:(1)见解析
(2)见解析
解析:(1)∵,,
∴,
在和中,
,
∴,
∴;
(2)证明:∵,
∴,
∵,
∴,
∴,即,
在和中,
,
∴,
∴.
4.如图,在四边形ACBD中,点P在对角线AB上,连接,,,.
试说明:(1);
(2).
答案:(1)见解析
(2)见解析
解析:(1)因为,所以.
在和中,
所以.
(2)由(1)知,,所以.
在和中,
所以,所以.
5.如图,在中,两边AB,AC上有两点M,N,D为外一点,且,,,.
(1)猜想线段MN,BM,CN之间的数量关系并说明理由.
(2)若,,求的周长.
答案:(1).理由见解析
(2)15
解析:(1).理由如下:
延长AB,在AB的延长线上取,连接DE,如图.
因为,,
所以.
又因为,所以.
因为,,,
所以,
所以,.
因为,
所以,
所以.
因为,,,
所以,所以.
因为,
所以.
(2)因为,,,
所以的周长为
.
题型5 ASA、AAS全等的实际应用
例5.小丽与爸爸、妈妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,与地面垂直,小丽两脚在地面上用力一蹬,妈妈在B处接住她后用力一堆,爸爸在C处接住她.若点B距离地面的高度为,点B到的距离为,点C距离地面的高度是,,则点C到的距离为 _____ 米.
条件识别
ASA :当已知条件中两个角及它们的夹边时直接使用。
AAS :当已知条件中两个角及其中一角的对边时使用
书写规范
用相同符号标记相等边,加粗或特殊符号突出条件顺序(如ASA需夹边在中间)。
注意区分“夹边”与“对边”,避免混淆。
证明步骤
ASA :先证明两角相等,再证明夹边相等,最后得出全等结论。
AAS :先证明两角相等,再证明其中一角的对边相等,通过三角形内角和推导出第三对角相等,最终证明全等。
答案:1.8
解析:点B距离地面的高度为,点C距离地面的高度是,
点D距离地面的高度为,点E距离地面的高度是,
,
,
,
,
又由题意可知,,
,
,,
,
点C到的距离为,
故答案为:1.8.
针对训练5
1.咸阳宫位于渭水之北,泾水之南,是中国历史上最恢宏壮丽的宫殿之一.某数学研究小组的同学们把测量咸阳宫城墙的高度作为一项课题活动,设计了如表所示的测量方案:
课题 测量咸阳宫城墙的高度
成员 组长:×××组员:×××,×××,×××
测量工具 测角仪、皮尺等
测量示意图
测量说明 如图,,,甲同学在小树与城墙之间的点E处,分别测得、,发现α与β互余
测量数据 米,米
请你根据上述信息求出咸阳宫城墙的高度.
答案:咸阳宫城墙的高度为18米.
解析:∵米,米,
∴(米).
∵,,
∴,
∴与互余,
∵α与β互余,,,
∴,
在和中,,,,
∴
∴(米).
答:咸阳宫城墙的高度为18米.
2.如图,小亮站在河边的点A处,在河的对面(小亮的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30米到达一棵树点C处,接着再向前走了30米到达点D处,然后他左转向南直行,当小亮看到电线塔、树与自己现处的位置E在一条直线上时,他共走了140米.
(1)根据题意,画出示意图;
(2)求小亮在点A处时他与电线塔的距离,并说明理由.
答案:(1)见详解
(2)80米,理由见详解
解析:根据题意可知米,米.
故可画示意图如下:
(2)根据题意可知:,
∴在和中 ,
∴,
∴米
∴小刚在点A处时他与电线塔的距离为80米.
3.如图,要测量河两岸相对的两点A、B的距离,可以在的垂线上取两点C、D,使,再过点D作,使A、C、E在一条直线上,这时测得的的长就是的长,你知道其中的道理吗?请给出你的证明.
答案:见解析
解析:证明:,,
,
又,,
,
.
4.综合与实践
【主题】军事训练中的距离测量问题
【素材】在某次重要的军事训练任务中,士兵小王肩负着一项关键使命:精准测量我方阵地(点A)与对岸目标(点B)之间的距离.然而,摆在小王面前的是诸多棘手难题,河流湍急无法直接过河,且身处野外环境没有携带任何专业测量工具.但小王凭借着扎实的数学知识和冷静的头脑,巧妙地运用了以下方法来解决这一难题:
【实践操作】如图所示:
步骤1:面向点B站立,调整目视高度,使视线恰好经过帽檐到达点;
步骤2:保持身体姿态不变,原地转过一个角度,标记此时视线落在河岸的点C;
步骤3:步测得米.已知小王身高为,帽顶O到眼睛D的垂直距离为.
【问题解决】
(1)如何测得我方阵地与对岸目标之间的距离?请用你所学数学知识说明.
(2)若将本题中的测量方法应用到生活场景中,例如测量池塘对岸某一物体的距离,你认为该方法是否同样适用?请举例说明在生活场景应用时可能会遇到的不同情况及相应的解决办法.
答案:(1)见解析
(2)见解析
解析:(1)由题意可得:,,
又,
,
米;
(2)该方法在生活场景中测量池塘对岸某一物体的距离同样适用,
可能会遇到的不同情况及相应的解决办法:
情况一:周围由障碍物影响视线,
解决办法:可以选择适合的观测点,避开障碍物,重新进行观测操作。或者借助梯子等工具,升高观测点位置,越过障碍物进行观测;
情况二:底面不平整影响站姿,
解决办法:可以先在地面上铺设一块平整的垫板,再进行测量操作.
5.学习《利用三角形全等测距离》后,“开拓”小组的同学就“测量河两岸A,B两点间的距离”这一问题,设计了如下方案:如图,在点B所在河岸同侧平地上取点C和点D.使点A,B,C在一条直线上,且,测得,,在CD的延长线上取一点E,使,这时测得DE的长就是A,B两点间的距离.你同意他们的说法吗?请说明理由.
答案:同意.理由见解析
解析:同意.理由如下:
因为,,
所以,
又因为,所以.
在和中,
所以,所以.
因为,
所以,即,
所以测得DE的长就是A,B两点间的距离.
创新拓展能力提升
1.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析;
(2)3.
解析:,
,
即:,
在和中,
,
∴,
;
(2)解析:由(1)得,
,
,,
.
2.如图1,已知中,,,AE是过点A的一条直线,点B,C在直线AE的两侧,于点D,于点E,.
(1)试说明:.
(2)若直线AE绕点A旋转到图2的位置,其余条件不变,则BD与DE,CE的关系如何?请说明理由.
(3)若直线AE绕点A旋转到图3的位置,其余条件不变,则BD与DE,CE的关系如何?请直接写出结果.
(4)归纳(1)(2)(3)问,请用简洁的语言表述BD,DE,CE的关系.
答案:(1)证明见解析
(2).理由见解析
(3)
(4)见解析
解析:(1)因为,所以.
又,,所以,
所以,所以.
在和中,
所以(AAS).
所以,.
因为,
所以.
(2).理由如下:
因为,
所以.
因为,,
所以,
所以,
所以.
在和中,
所以(AAS),
所以,.
因为,
所以.
(3).
(4)当点B,C在直线AE的异侧时,;当点B,C在直线AE的同侧时,.
3.如图,在平面直角坐标系中,已知点、分别为x轴和y轴上一点,且a,b满足,过点B作于点E,延长至点D,使得,连接、,平分.
(1)A点的坐标为;的度数为.
(2)如图1,若点C在第四象限,试判断与的数量关系与位置关系,并说明理由.
(3)如图2,连接,平分,若点C的坐标为,连接交于点E,与交于点F.
①求D点的坐标;
②试判断与的数量关系,并说明理由.
答案:(1),
(2),
(3)①;②
解析:(1),
,
,
,,
,
,
故答案为:,;
(2)设与y轴的交点为G,与x轴的交点为H,
,
,
,
,,
,
,,
,
,,
,
,
,
,
;
(3)①由(2)可知,,过点D作轴交x轴于K,
,,
,
,
,
,,
点C的坐标为,
,,
;
②延长交于点M,
,
,
,,
,
,,
平分,
,
,,
,
,
.
典例精讲
名师支招
名师支招
名师支招
名师支招
名师支招
典例精讲
名师支招
名师支招
名师支招
名师支招
名师支招
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年新八年级数学人教版暑假大讲堂
第十讲 全等三角形判定二
知识点梳理
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
要点诠释:
夹边要求:必须是两角的公共边
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
要点诠释:
当已知条件中涉及两角及非夹边时,优先使用AAS判定。例如,已知两角和其中一角的对边相等,可直接套用AAS定理
知识点3判定方法的选择
选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS
要点诠释:
如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
题型1 添加条件使能够运用ASA、AAS判定三角形全等
例1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
避免混淆 :ASA要求夹边,AAS要求非夹边;
隐含条件 :对顶角、公共边等可辅助证明;
反例说明 :AAA(三个角相等)不能判定全等
针对训练1
1.如图,在和中,点A,E,B,D在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
2.如图,D在上,E在上,且.补充下列一个条件后,仍无法判定的是( )
A. B. C. D.
3.如图,与相交于点O,,,不添加辅助线,判定的依据是( )
A. B. C. D.
4.在中,,,,下列条件能得到的是( )
A.,, B.,,
C.,, D.,,
5.如图,点B、F、C、E在一条直线上,,,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
题型2 利用ASA全等证明线段相等
例2.如图,在与中,已知,,,若,,则_________.
需准确识别夹边条件,避免混淆非对应边。
结合其他定理(如等腰三角形三线合一)可简化证明过程
针对训练2
1.如图,,,,且.
求证:.
2.如图,已知,,,.求证:.
3.如图,在中,D是上一点,E是外一点,,,.求证:.
4.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
5.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
题型3 利用AAS全等证明线段相等
例3.如图,,且.E、F是上两点,,.若,,,则的长为_____ .
转化思路 :若条件中未直接给出AAS,可通过三角形内角和定理将两角及其中一角的对边转化为AAS形式。例如,已知两角及非对边相等时,可证明第三个角也相等,从而满足AAS。
辅助线添加 :在复杂图形中,适当添加辅助线(如作高、中线或延长线)构造全等三角形。例如,在直角三角形中,利用斜边中线性质辅助证明
针对训练3
1.如图,在中,,是的平分线,于E,F在上,,试证明:
(1).
(2).
2.如图,已知:,求证:
3.已知:如图,,点D是的中点,平分,,垂足为E.
求证:.
4.如图,已知在四边形中,点E在上,,,.
(1)求证:;
(2)若,,求的度数.
.
5.已知:如图,点A、B、E在同一直线上,且,,
求证:
题型4 全等三角形判定方法选择
例4.综合与探究
问题情境:在中,,,点D在直线上运动,连接,将线段绕点A顺时针旋转得到线段,过点E作,交直线于点F.
探究发现:
(1)如图1,当点D在上时,与的数量关系是__________.
(2)如图2,当点D在的延长线上时,连接交于点H.求证:.
拓展思考:
(3)当,时,直接写出的面积.
已知两边及夹角 :直接用SAS;
已知两角及一边 :用ASA或AAS;
等腰三角形 :结合SAS或ASA;
中点、角平分线 :通过构造全等三角形辅助证明
针对训练4
1.如图,的边AB与的边ED相交于点F,连接CF.已知,,.
(1)求证:;
(2)求证:FC平分.
2.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
3.如图,在中,,延长至点E,过点E作,使,连接交于点D.
(1)求证:;
(2)若G是上一点,满足,连接,证明:.
4.如图,在四边形ACBD中,点P在对角线AB上,连接,,,.
试说明:(1);
(2).
5.如图,在中,两边AB,AC上有两点M,N,D为外一点,且,,,.
(1)猜想线段MN,BM,CN之间的数量关系并说明理由.
(2)若,,求的周长.
题型5 ASA、AAS全等的实际应用
例5.小丽与爸爸、妈妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,与地面垂直,小丽两脚在地面上用力一蹬,妈妈在B处接住她后用力一堆,爸爸在C处接住她.若点B距离地面的高度为,点B到的距离为,点C距离地面的高度是,,则点C到的距离为 _____ 米.
条件识别
ASA :当已知条件中两个角及它们的夹边时直接使用。
AAS :当已知条件中两个角及其中一角的对边时使用
书写规范
用相同符号标记相等边,加粗或特殊符号突出条件顺序(如ASA需夹边在中间)。
注意区分“夹边”与“对边”,避免混淆。
证明步骤
ASA :先证明两角相等,再证明夹边相等,最后得出全等结论。
AAS :先证明两角相等,再证明其中一角的对边相等,通过三角形内角和推导出第三对角相等,最终证明全等。
针对训练5
1.咸阳宫位于渭水之北,泾水之南,是中国历史上最恢宏壮丽的宫殿之一.某数学研究小组的同学们把测量咸阳宫城墙的高度作为一项课题活动,设计了如表所示的测量方案:
课题 测量咸阳宫城墙的高度
成员 组长:×××组员:×××,×××,×××
测量工具 测角仪、皮尺等
测量示意图
测量说明 如图,,,甲同学在小树与城墙之间的点E处,分别测得、,发现α与β互余
测量数据 米,米
请你根据上述信息求出咸阳宫城墙的高度.
2.如图,小亮站在河边的点A处,在河的对面(小亮的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30米到达一棵树点C处,接着再向前走了30米到达点D处,然后他左转向南直行,当小亮看到电线塔、树与自己现处的位置E在一条直线上时,他共走了140米.
(1)根据题意,画出示意图;
(2)求小亮在点A处时他与电线塔的距离,并说明理由.
3.如图,要测量河两岸相对的两点A、B的距离,可以在的垂线上取两点C、D,使,再过点D作,使A、C、E在一条直线上,这时测得的的长就是的长,你知道其中的道理吗?请给出你的证明.
4.综合与实践
【主题】军事训练中的距离测量问题
【素材】在某次重要的军事训练任务中,士兵小王肩负着一项关键使命:精准测量我方阵地(点A)与对岸目标(点B)之间的距离.然而,摆在小王面前的是诸多棘手难题,河流湍急无法直接过河,且身处野外环境没有携带任何专业测量工具.但小王凭借着扎实的数学知识和冷静的头脑,巧妙地运用了以下方法来解决这一难题:
【实践操作】如图所示:
步骤1:面向点B站立,调整目视高度,使视线恰好经过帽檐到达点;
步骤2:保持身体姿态不变,原地转过一个角度,标记此时视线落在河岸的点C;
步骤3:步测得米.已知小王身高为,帽顶O到眼睛D的垂直距离为.
【问题解决】
(1)如何测得我方阵地与对岸目标之间的距离?请用你所学数学知识说明.
(2)若将本题中的测量方法应用到生活场景中,例如测量池塘对岸某一物体的距离,你认为该方法是否同样适用?请举例说明在生活场景应用时可能会遇到的不同情况及相应的解决办法.
5.学习《利用三角形全等测距离》后,“开拓”小组的同学就“测量河两岸A,B两点间的距离”这一问题,设计了如下方案:如图,在点B所在河岸同侧平地上取点C和点D.使点A,B,C在一条直线上,且,测得,,在CD的延长线上取一点E,使,这时测得DE的长就是A,B两点间的距离.你同意他们的说法吗?请说明理由.
创新拓展能力提升
1.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
2.如图1,已知中,,,AE是过点A的一条直线,点B,C在直线AE的两侧,于点D,于点E,.
(1)试说明:.
(2)若直线AE绕点A旋转到图2的位置,其余条件不变,则BD与DE,CE的关系如何?请说明理由.
(3)若直线AE绕点A旋转到图3的位置,其余条件不变,则BD与DE,CE的关系如何?请直接写出结果.
(4)归纳(1)(2)(3)问,请用简洁的语言表述BD,DE,CE的关系.
3.如图,在平面直角坐标系中,已知点、分别为x轴和y轴上一点,且a,b满足,过点B作于点E,延长至点D,使得,连接、,平分.
(1)A点的坐标为;的度数为.
(2)如图1,若点C在第四象限,试判断与的数量关系与位置关系,并说明理由.
(3)如图2,连接,平分,若点C的坐标为,连接交于点E,与交于点F.
①求D点的坐标;
②试判断与的数量关系,并说明理由.
2025年新八年级数学人教版暑假大讲堂
第十讲 全等三角形判定二(解析版)
知识点梳理
知识点1 判定三角形全等的方法---角边角 (ASA)
(1)两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(SAS).
要点诠释:
夹边要求:必须是两角的公共边
知识点2 判定三角形全等的方法---角角边 (AAS)
(1)两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
(2)书写格式:如图所示,在列举两个三角形全等的条件时,如:
在△ABC和△A′B′C′中,
∠A=∠A′
∠B=∠B′
AC=A′C′
∴△ABC≌△A′B′C′(SAS).
由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
要点诠释:
当已知条件中涉及两角及非夹边时,优先使用AAS判定。例如,已知两角和其中一角的对边相等,可直接套用AAS定理
知识点3判定方法的选择
选择哪种判定方法,要根据具体的已知条件而定,见下表:
已知条件 可选择的判定方法
一边一角对应相等 SAS AAS ASA
两角对应相等 ASA AAS
两边对应相等 SAS
要点诠释:
如何选择三角形证全等
(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
(2)可以从已知出发,看已知条件确定证哪两个三角形全等;
(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.
注意: 三个角对应相等的两个三角形不一定全等.
题型1 添加条件使能够运用ASA、AAS判定三角形全等
例1.如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是____________(不添加任何辅助线).
避免混淆 :ASA要求夹边,AAS要求非夹边;
隐含条件 :对顶角、公共边等可辅助证明;
反例说明 :AAA(三个角相等)不能判定全等
【答案】∠A=∠D(答案不唯一).
【解析】先说明∠ACB=∠DCE,再添加∠A=∠D,再结合BC=EC运用AAS即可证明△ABC≌△DEC.
解:添加条件:∠A=∠D;
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA即∠ACB=∠DCE
在△ABC和△DEC中
∠A=∠D ,∠ACB=∠DCE,BC=EC
∴△ABC≌△DEC(AAS).
故答案为:∠A=∠D(答案不唯一).
【点睛】本题考查了全等三角形的判定定理;掌握全等三角形的判定方法是解答本题的关键.
针对训练1
1.如图,在和中,点A,E,B,D在同一直线上,,,只添加一个条件,能判定的是( )
A. B. C. D.
答案:B
解析:因为,所以.因为,所以添加,无法判定;
添加,则,即,根据“SAS”可判定;
添加,无法判定;
添加,无法判定.
2.如图,D在上,E在上,且.补充下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:B
解析:∵,,
∴要使全等,只需要一组对应边对应相等即可,
∴当或或时,,
当时,三组对应角相等,不能判定,
故选B.
3.如图,与相交于点O,,,不添加辅助线,判定的依据是( )
A. B. C. D.
答案:B
解析:在与中,
,
∴;
故选:B.
4.在中,,,,下列条件能得到的是( )
A.,, B.,,
C.,, D.,,
答案:C
解析:∵,
∴,,,
∴,
故选C.
5.如图,点B、F、C、E在一条直线上,,,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
答案:C
解析:选项A、添加可用AAS进行判定,故本选不符合题意;
选项B、添加可用AAS进行判定,故本选项不符合题意;
选项C、添加不能判定,故本选项符合题意;
选项D、添加可得出,然后可用ASA进行判定,故本选项不符合题意.
故选C.
题型2 利用ASA全等证明线段相等
例2.如图,在与中,已知,,,若,,则_________.
需准确识别夹边条件,避免混淆非对应边。
结合其他定理(如等腰三角形三线合一)可简化证明过程
答案:10
解析:∵,
∴,
又∵,,
∴,
∴,
∵,,
∴,
∴,
故答案为:10.
针对训练2
1.如图,,,,且.
求证:.
答案:见解析.
解析:∵,,
∴,,
∴.
又,,
∴.
∴.
2.如图,已知,,,.求证:.
答案:见解析
解析:证明:∵,
∴,
∴,
∵,,
∴,
∴.
3.如图,在中,D是上一点,E是外一点,,,.求证:.
答案:见解析
解析:∵,
则,
∴,
在和中,
,
∴,
∴.
4.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
答案:(1)见解析
(2).
解析:(1)证明:,
,
;
,
,
;
在和中,
,
;
(2),,
,,
,
,
.
5.已知:如图,,,垂足分别为B,E,,相交于点F,且.
(1)求证:;
(2)已知,,求的长度.
答案:(1)见解析
(2).
解析:(1)证明:,
,
;
,
,
;
在和中,
,
;
(2),,
,,
,
,
.
题型3 利用AAS全等证明线段相等
例3.如图,,且.E、F是上两点,,.若,,,则的长为_____ .
转化思路 :若条件中未直接给出AAS,可通过三角形内角和定理将两角及其中一角的对边转化为AAS形式。例如,已知两角及非对边相等时,可证明第三个角也相等,从而满足AAS。
辅助线添加 :在复杂图形中,适当添加辅助线(如作高、中线或延长线)构造全等三角形。例如,在直角三角形中,利用斜边中线性质辅助证明
答案:6
解析:∵,,
∴,,
∴,
在和中,
,
∴
∴,,
∵
∴
∴
故答案是:6.
针对训练3
1.如图,在中,,是的平分线,于E,F在上,,试证明:
(1).
(2).
答案:(1)见解析
(2)见解析
解析:(1)证明:∵是的平分线,
∴,
∵,
∴,
又∵,
∴,
∴,
又∵,,
∴,
∴;
(2)证明:∵,
∴,
∵,
∴,
∵,
∴.
2.如图,已知:,求证:
答案:见解析
解析:,
∴,
即,
在和中,
,
∴,
∴.
3.已知:如图,,点D是的中点,平分,,垂足为E.
求证:.
答案:见解析
解析:∵,点D是的中点,
∴,
∴.
∵,
∴.
∵平分,
∴.
在和中,,,,
∴,
∴.
4.如图,已知在四边形中,点E在上,,,.
(1)求证:;
(2)若,,求的度数.
答案:(1)证明见解析;(2)
解析:∵,
∴,
∴,
在和中,
,
∴,
∴;
(2)∵,,
∴
∵,
∴.
5.已知:如图,点A、B、E在同一直线上,且,,
求证:
答案:见解析.
解析:
在与中
题型4 全等三角形判定方法选择
例4.综合与探究
问题情境:在中,,,点D在直线上运动,连接,将线段绕点A顺时针旋转得到线段,过点E作,交直线于点F.
探究发现:
(1)如图1,当点D在上时,与的数量关系是__________.
(2)如图2,当点D在的延长线上时,连接交于点H.求证:.
拓展思考:
(3)当,时,直接写出的面积.
已知两边及夹角 :直接用SAS;
已知两角及一边 :用ASA或AAS;
等腰三角形 :结合SAS或ASA;
中点、角平分线 :通过构造全等三角形辅助证明
答案:(1)
(2)见解析
(3)12或24
解析:∵,
∴,
又∵,
∴,
∴,
由旋转得,,
又∵,
∴,
∴,
在和中,
∴,
∴;
(2)由旋转得,,
∵,
∴,
∵,
∴,
∵,
∴,
又在中,,
∴,即,
在和中,
∴,
∴,
又,
∴,
∵,且,
∴,
又,
∴
在和中,
∴,
∴;
(3)∵,,
∴当点D在的延长线上时,,不满足题意,
∴点D在上,由(1)知,
∴,
∴,
∵,
∴.
当点D在的延长线上时,如图,
同理可得,,,
∴,
综上,的面积为12或24.
针对训练4
1.如图,的边AB与的边ED相交于点F,连接CF.已知,,.
(1)求证:;
(2)求证:FC平分.
答案:(1)见解析
(2)见解析
解析:(1)∵,
∴,
即,
在与中
,
∴,
∴;
(2)过点C作,,垂足分别为G,H,
∵,
∴,
∵,,
∴,
在与中
,
∴,
∴,
∴FC平分.
2.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析;
(2)3.
解析:,
,
即:,
在和中,
,
∴,
;
(2)解析:由(1)得,
,
,,
.
3.如图,在中,,延长至点E,过点E作,使,连接交于点D.
(1)求证:;
(2)若G是上一点,满足,连接,证明:.
答案:(1)见解析
(2)见解析
解析:(1)∵,,
∴,
在和中,
,
∴,
∴;
(2)证明:∵,
∴,
∵,
∴,
∴,即,
在和中,
,
∴,
∴.
4.如图,在四边形ACBD中,点P在对角线AB上,连接,,,.
试说明:(1);
(2).
答案:(1)见解析
(2)见解析
解析:(1)因为,所以.
在和中,
所以.
(2)由(1)知,,所以.
在和中,
所以,所以.
5.如图,在中,两边AB,AC上有两点M,N,D为外一点,且,,,.
(1)猜想线段MN,BM,CN之间的数量关系并说明理由.
(2)若,,求的周长.
答案:(1).理由见解析
(2)15
解析:(1).理由如下:
延长AB,在AB的延长线上取,连接DE,如图.
因为,,
所以.
又因为,所以.
因为,,,
所以,
所以,.
因为,
所以,
所以.
因为,,,
所以,所以.
因为,
所以.
(2)因为,,,
所以的周长为
.
题型5 ASA、AAS全等的实际应用
例5.小丽与爸爸、妈妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,与地面垂直,小丽两脚在地面上用力一蹬,妈妈在B处接住她后用力一堆,爸爸在C处接住她.若点B距离地面的高度为,点B到的距离为,点C距离地面的高度是,,则点C到的距离为 _____ 米.
条件识别
ASA :当已知条件中两个角及它们的夹边时直接使用。
AAS :当已知条件中两个角及其中一角的对边时使用
书写规范
用相同符号标记相等边,加粗或特殊符号突出条件顺序(如ASA需夹边在中间)。
注意区分“夹边”与“对边”,避免混淆。
证明步骤
ASA :先证明两角相等,再证明夹边相等,最后得出全等结论。
AAS :先证明两角相等,再证明其中一角的对边相等,通过三角形内角和推导出第三对角相等,最终证明全等。
答案:1.8
解析:点B距离地面的高度为,点C距离地面的高度是,
点D距离地面的高度为,点E距离地面的高度是,
,
,
,
,
又由题意可知,,
,
,,
,
点C到的距离为,
故答案为:1.8.
针对训练5
1.咸阳宫位于渭水之北,泾水之南,是中国历史上最恢宏壮丽的宫殿之一.某数学研究小组的同学们把测量咸阳宫城墙的高度作为一项课题活动,设计了如表所示的测量方案:
课题 测量咸阳宫城墙的高度
成员 组长:×××组员:×××,×××,×××
测量工具 测角仪、皮尺等
测量示意图
测量说明 如图,,,甲同学在小树与城墙之间的点E处,分别测得、,发现α与β互余
测量数据 米,米
请你根据上述信息求出咸阳宫城墙的高度.
答案:咸阳宫城墙的高度为18米.
解析:∵米,米,
∴(米).
∵,,
∴,
∴与互余,
∵α与β互余,,,
∴,
在和中,,,,
∴
∴(米).
答:咸阳宫城墙的高度为18米.
2.如图,小亮站在河边的点A处,在河的对面(小亮的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30米到达一棵树点C处,接着再向前走了30米到达点D处,然后他左转向南直行,当小亮看到电线塔、树与自己现处的位置E在一条直线上时,他共走了140米.
(1)根据题意,画出示意图;
(2)求小亮在点A处时他与电线塔的距离,并说明理由.
答案:(1)见详解
(2)80米,理由见详解
解析:根据题意可知米,米.
故可画示意图如下:
(2)根据题意可知:,
∴在和中 ,
∴,
∴米
∴小刚在点A处时他与电线塔的距离为80米.
3.如图,要测量河两岸相对的两点A、B的距离,可以在的垂线上取两点C、D,使,再过点D作,使A、C、E在一条直线上,这时测得的的长就是的长,你知道其中的道理吗?请给出你的证明.
答案:见解析
解析:证明:,,
,
又,,
,
.
4.综合与实践
【主题】军事训练中的距离测量问题
【素材】在某次重要的军事训练任务中,士兵小王肩负着一项关键使命:精准测量我方阵地(点A)与对岸目标(点B)之间的距离.然而,摆在小王面前的是诸多棘手难题,河流湍急无法直接过河,且身处野外环境没有携带任何专业测量工具.但小王凭借着扎实的数学知识和冷静的头脑,巧妙地运用了以下方法来解决这一难题:
【实践操作】如图所示:
步骤1:面向点B站立,调整目视高度,使视线恰好经过帽檐到达点;
步骤2:保持身体姿态不变,原地转过一个角度,标记此时视线落在河岸的点C;
步骤3:步测得米.已知小王身高为,帽顶O到眼睛D的垂直距离为.
【问题解决】
(1)如何测得我方阵地与对岸目标之间的距离?请用你所学数学知识说明.
(2)若将本题中的测量方法应用到生活场景中,例如测量池塘对岸某一物体的距离,你认为该方法是否同样适用?请举例说明在生活场景应用时可能会遇到的不同情况及相应的解决办法.
答案:(1)见解析
(2)见解析
解析:(1)由题意可得:,,
又,
,
米;
(2)该方法在生活场景中测量池塘对岸某一物体的距离同样适用,
可能会遇到的不同情况及相应的解决办法:
情况一:周围由障碍物影响视线,
解决办法:可以选择适合的观测点,避开障碍物,重新进行观测操作。或者借助梯子等工具,升高观测点位置,越过障碍物进行观测;
情况二:底面不平整影响站姿,
解决办法:可以先在地面上铺设一块平整的垫板,再进行测量操作.
5.学习《利用三角形全等测距离》后,“开拓”小组的同学就“测量河两岸A,B两点间的距离”这一问题,设计了如下方案:如图,在点B所在河岸同侧平地上取点C和点D.使点A,B,C在一条直线上,且,测得,,在CD的延长线上取一点E,使,这时测得DE的长就是A,B两点间的距离.你同意他们的说法吗?请说明理由.
答案:同意.理由见解析
解析:同意.理由如下:
因为,,
所以,
又因为,所以.
在和中,
所以,所以.
因为,
所以,即,
所以测得DE的长就是A,B两点间的距离.
创新拓展能力提升
1.如图,四边形中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析;
(2)3.
解析:,
,
即:,
在和中,
,
∴,
;
(2)解析:由(1)得,
,
,,
.
2.如图1,已知中,,,AE是过点A的一条直线,点B,C在直线AE的两侧,于点D,于点E,.
(1)试说明:.
(2)若直线AE绕点A旋转到图2的位置,其余条件不变,则BD与DE,CE的关系如何?请说明理由.
(3)若直线AE绕点A旋转到图3的位置,其余条件不变,则BD与DE,CE的关系如何?请直接写出结果.
(4)归纳(1)(2)(3)问,请用简洁的语言表述BD,DE,CE的关系.
答案:(1)证明见解析
(2).理由见解析
(3)
(4)见解析
解析:(1)因为,所以.
又,,所以,
所以,所以.
在和中,
所以(AAS).
所以,.
因为,
所以.
(2).理由如下:
因为,
所以.
因为,,
所以,
所以,
所以.
在和中,
所以(AAS),
所以,.
因为,
所以.
(3).
(4)当点B,C在直线AE的异侧时,;当点B,C在直线AE的同侧时,.
3.如图,在平面直角坐标系中,已知点、分别为x轴和y轴上一点,且a,b满足,过点B作于点E,延长至点D,使得,连接、,平分.
(1)A点的坐标为;的度数为.
(2)如图1,若点C在第四象限,试判断与的数量关系与位置关系,并说明理由.
(3)如图2,连接,平分,若点C的坐标为,连接交于点E,与交于点F.
①求D点的坐标;
②试判断与的数量关系,并说明理由.
答案:(1),
(2),
(3)①;②
解析:(1),
,
,
,,
,
,
故答案为:,;
(2)设与y轴的交点为G,与x轴的交点为H,
,
,
,
,,
,
,,
,
,,
,
,
,
,
;
(3)①由(2)可知,,过点D作轴交x轴于K,
,,
,
,
,
,,
点C的坐标为,
,,
;
②延长交于点M,
,
,
,,
,
,,
平分,
,
,,
,
,
.
典例精讲
名师支招
名师支招
名师支招
名师支招
名师支招
典例精讲
名师支招
名师支招
名师支招
名师支招
名师支招
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
