数学:2.2《椭圆的几何性质(3)》课件(苏教版选修1-1)
文档属性
| 名称 | 数学:2.2《椭圆的几何性质(3)》课件(苏教版选修1-1) |  | |
| 格式 | rar | ||
| 文件大小 | 661.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-25 13:23:00 | ||
图片预览






文档简介
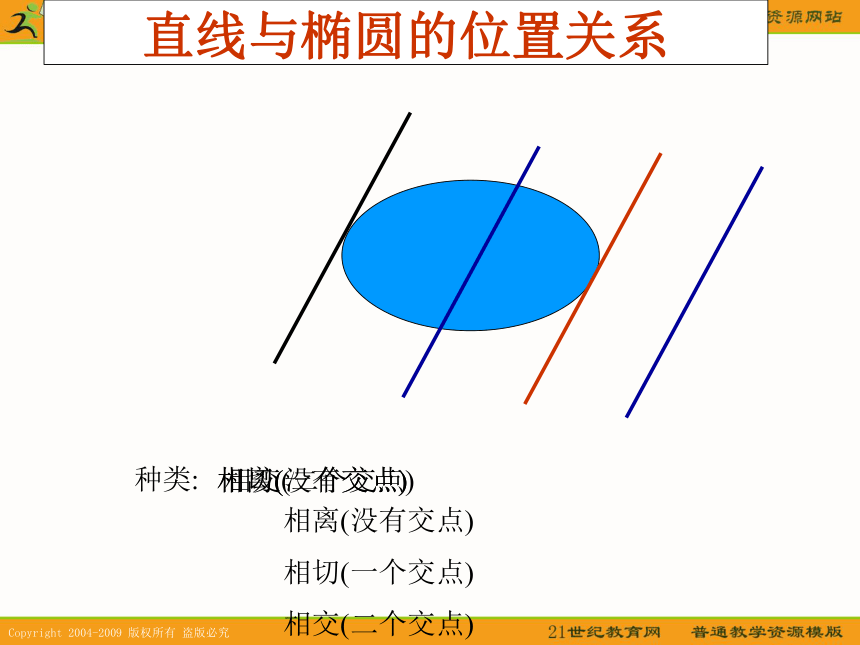
课件18张PPT。直线与椭圆的位置关系直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法例1:直线y=kx+1与椭圆 恒有公共点,
求m的取值范围。例4.Mll1xyF2F1O注: 是椭圆上的点到焦点的距离,常把它们叫做焦半径。例5 已知椭圆5x2+9y2=45,椭圆的右焦点为F,
(1)求过点F且斜率为1的直线被椭圆截得的弦长.
(2)判断点A(1,1)与椭圆的位置关系,并求以A为中点
椭圆的弦所在的直线方程.
引申:当点P与两焦点连线成钝角时,求P点的横坐标
的取值范围.例6:求椭圆 上一点P,使得点P与椭圆
两焦点连线互相垂直.法二【练习】(a>b>0)上一点, 是两个焦点,半焦距为c,则 的最大值与最小值之差一定是( ).A. 1 B. C. D.xOyPFQDBA(a>b>0),F为焦点,A为顶点,准线l交x轴于B,P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则椭圆( )A. 1个 B. 3个 C. 4个 D. 5个DD2、弦长公式:
设直线 l与椭圆C 相交于A( x1 ,y1) ,B( x2,y2 ),
则 |AB|= , 其中 k 是直线的斜率1、判断直线与椭圆位置关系的方法:
解方程组消去其中一元得一元二次型方程3、处理弦中点问题:“点差法”、“韦达定理”小结
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法例1:直线y=kx+1与椭圆 恒有公共点,
求m的取值范围。例4.Mll1xyF2F1O注: 是椭圆上的点到焦点的距离,常把它们叫做焦半径。例5 已知椭圆5x2+9y2=45,椭圆的右焦点为F,
(1)求过点F且斜率为1的直线被椭圆截得的弦长.
(2)判断点A(1,1)与椭圆的位置关系,并求以A为中点
椭圆的弦所在的直线方程.
引申:当点P与两焦点连线成钝角时,求P点的横坐标
的取值范围.例6:求椭圆 上一点P,使得点P与椭圆
两焦点连线互相垂直.法二【练习】(a>b>0)上一点, 是两个焦点,半焦距为c,则 的最大值与最小值之差一定是( ).A. 1 B. C. D.xOyPFQDBA(a>b>0),F为焦点,A为顶点,准线l交x轴于B,P,Q在椭圆上,且PD⊥l于D,QF⊥AO,则椭圆( )A. 1个 B. 3个 C. 4个 D. 5个DD2、弦长公式:
设直线 l与椭圆C 相交于A( x1 ,y1) ,B( x2,y2 ),
则 |AB|= , 其中 k 是直线的斜率1、判断直线与椭圆位置关系的方法:
解方程组消去其中一元得一元二次型方程3、处理弦中点问题:“点差法”、“韦达定理”小结
