2024-2025高三物理力学复习同步练习经典计算题型训练(含解析)
文档属性
| 名称 | 2024-2025高三物理力学复习同步练习经典计算题型训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 802.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-06 00:00:00 | ||
图片预览



文档简介
2024-2025高三物理力学复习同步练习经典计算题型训练
1.如图所示,一不可伸长的轻绳跨过定滑轮分别连接木板A和小物块B(可看作质点),A的长度为,在水平地面上向右做速度大小为的匀速直线运动,B的下方悬有一水滴,与B一起在距离地面高处的水平光滑轨道上向左运动。当轻绳与水平方向夹角时,脱落,恰好落在A的右端。已知,滑轮可看做质点,不计A的厚度,不计空气阻力,取重力加速度大小,。求
(1)脱落时,B的速度大小;
(2)轻绳的长度;
(3)若使落在A上,A的速度应满足什么条件?
2.如图所示,不可伸长的轻绳穿过一竖直固定的光滑细管(半径可忽略),两端系有小球A、B(均可视为质点)。当小球A绕中心轴匀速转动时,小球B静止,小球A到上管口的绳长L=1m,与小球A相连的绳与竖直方向的夹角θ=60°。取重力加速度大小g=10m/s2,不计空气阻力。
(1)求小球A的质量m1与小球B的质量m2的比值;
(2)求小球A匀速转动的角速度大小ω;
(3)若小球A的角速度缓慢增大为原来的2倍,求重新稳定后小球B的高度变化量 h。
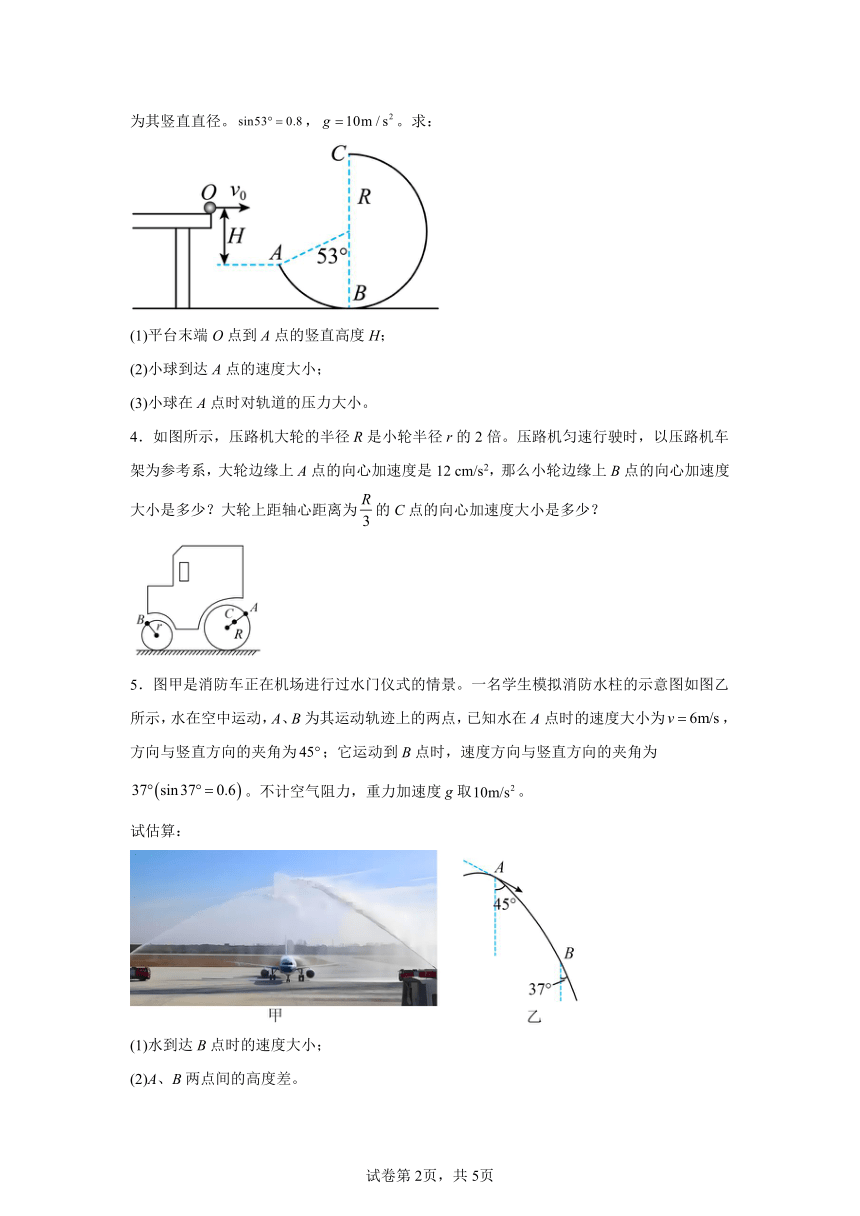
3.如图所示,将一质量为的小球自水平平台右端O点以一定的初速度水平抛出,小球飞离平台后经0.4s由A点沿切线落入竖直光滑圆轨道ABC,轨道半径,CB为其竖直直径。,。求:
(1)平台末端O点到A点的竖直高度H;
(2)小球到达A点的速度大小;
(3)小球在A点时对轨道的压力大小。
4.如图所示,压路机大轮的半径R是小轮半径r的2倍。压路机匀速行驶时,以压路机车架为参考系,大轮边缘上A点的向心加速度是12 cm/s2,那么小轮边缘上B点的向心加速度大小是多少?大轮上距轴心距离为的C点的向心加速度大小是多少?
5.图甲是消防车正在机场进行过水门仪式的情景。一名学生模拟消防水柱的示意图如图乙所示,水在空中运动,A、B为其运动轨迹上的两点,已知水在A点时的速度大小为,方向与竖直方向的夹角为;它运动到B点时,速度方向与竖直方向的夹角为。不计空气阻力,重力加速度g取。
试估算:
(1)水到达B点时的速度大小;
(2)A、B两点间的高度差。
6.如图所示为自行车的传动装置示意图,已知链轮的半径,飞轮的半径,后轮的半径,A、B、C(图中未画出)分别为链轮、飞轮和后轮边缘上的点。若脚蹬匀速转动一圈所需要的时间为,则在自行车匀速前进的过程中,求:
(1)A、B、C三点的向心加速度大小之比是多少?
(2)A、B、C三点的线速度大小之比是多少?
(3)自行车前进的速度大小约为多大?
(4)链轮、飞轮和后轮的角速度大小之比为多少?
7.如图所示为儿童迫击炮,在一次游戏活动中,某儿童用迫击炮轰击和炮在同一水平线上的目标。第一次发射时,炮筒与水平面之间的仰角为时,着弹点比目标近了一段距离;当第二次发射时,炮筒与水平面之间的仰角为时,着弹点比目标远了一段距离。已知炮弹每次离开炮口时的速度大小相等,重力加速度为g(g取),不计空气阻力,忽略炮口与目标之间的高度差。求:
(1)目标与迫击炮之间的距离d;
(2)炮弹离开炮口时的速度大小。
8.如图所示,足够长的竖直轨道AB与半圆槽BCD在同一竖直面内,O点为半圆槽的圆心,B、D点的连线水平,C为圆槽的最低点。安装在竖直轨道AB上的弹射器可上下移动,能水平向右发射出不同速率的弹丸(视为质点,出射点处于B点正上方)。已知半圆槽的半径R=3m,P点为半圆槽上O点右侧的一点,∠POD=θ=53°。取重力加速度大小g=10m/s2,sin53°=0.8,cos53°=0.6,不计空气阻力。
(1)调整弹射器的位置,使得弹丸出射点到B点的距离d1=4.8m,水平向右发射弹丸后弹丸恰好落在P点,求弹丸的初速度大小v1;
(2)调整弹射器的位置和弹丸的出射速率,使得弹丸均能击中半圆槽上的P点,求弹丸落到P点的最小速率vmin;
(3)调整弹射器的位置和弹丸的出射速率,使得弹丸垂直击中半圆槽上O点右侧的Q点(图中未画出),若已知弹丸击中Q点时的速度方向与水平方向的夹角为α(0<α<90°),求弹丸出射点到B点的距离d和弹丸击中Q点时的速度大小v。(均用α表示)
9.如图所示,质量均为M=9kg,厚度相同、长度均为L=0.6m的木板A、B(上表面粗糙)并排静止在光滑水平面上。质量m=18kg大小可忽略的机器猫静止于A板左端,机器描从A板左端斜向上跳出后,恰好落到A木板的右端,并立即与A板达到共速。随即以与第一次相同的速度起跳并落到B板上,机器猫落到B板上时碰撞时间极短可忽略,且不反弹。空气阻力可忽略,重力加速度为g=10m/s2。
(1)求从机器猫起跳至落在A板右端过程中A板运动的距离;
(2)求起跳速度与水平方向夹角为多少?可使机器猫起跳消耗的能量最少;
(3)新型材料制成的机器猫其质量仅为m′=7kg其他条件保持不变,机器猫总是以(2)问中的方式起跳,机器猫与B木板间的动摩擦因数为,求机器猫在B木板上的运动时间(结果保留两位小数)。
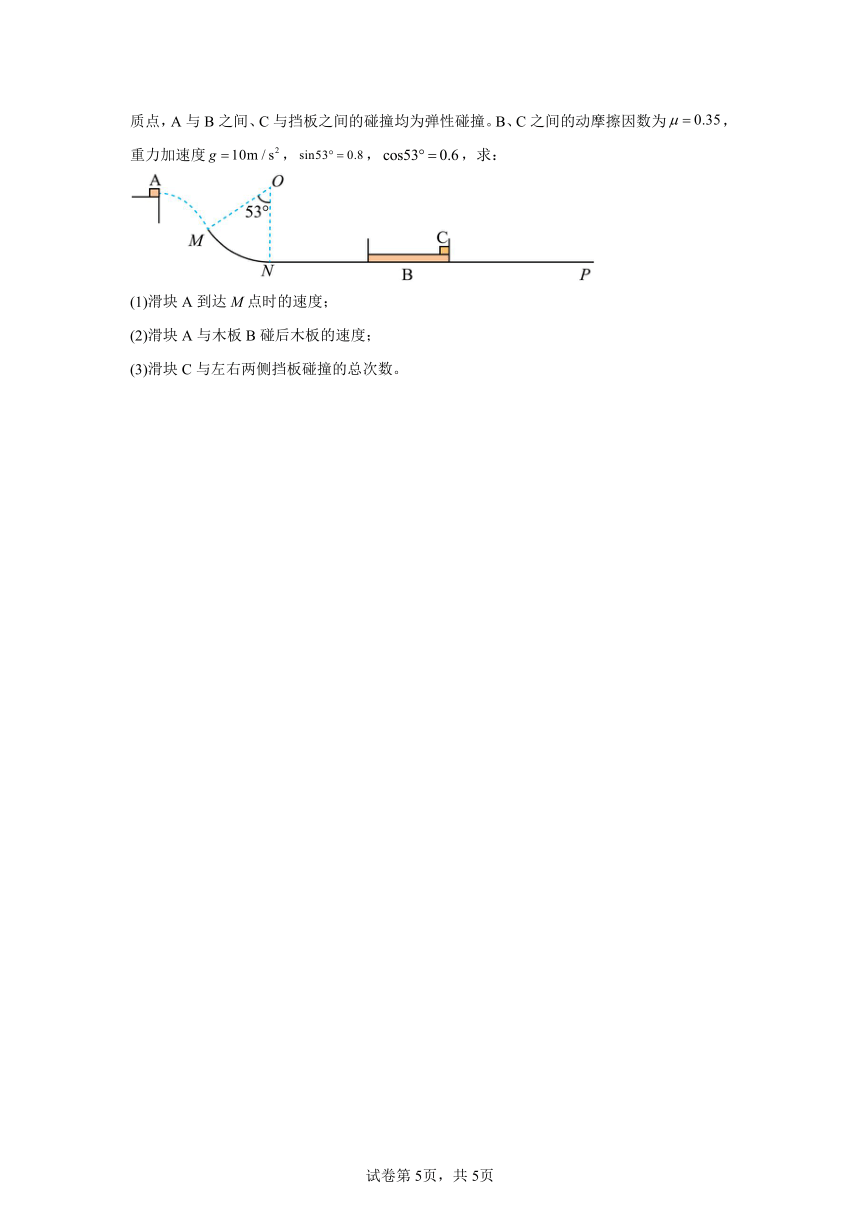
10.如图,MNP为一段光滑轨道,其中MN段是半径为的圆弧形轨道,M与圆心的连线与竖直方向夹角为53°。NP是水平足够长直轨道,MN与NP段在N点平滑连接。滑块A从距M点高度。处水平抛出,恰好能从M点切入轨道。在水平轨道某位置静止放置一长的木板B,木板左右两侧各有一固定挡板。木板紧靠右挡板放置一滑块C。滑块A在NP轨道上与木板B发生碰撞。若A、B、C三者质量相等,滑块A、C均可视为质点,A与B之间、C与挡板之间的碰撞均为弹性碰撞。B、C之间的动摩擦因数为,重力加速度,,,求:
(1)滑块A到达M点时的速度;
(2)滑块A与木板B碰后木板的速度;
(3)滑块C与左右两侧挡板碰撞的总次数。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.(1)
(2)
(3)
【详解】(1)木板A的速度大小等于小物块B沿轻绳方向的分速度
解得
(2)由几何知:P脱落瞬间B所在位置到滑轮间的轻绳距离
P脱落后做平抛运动,竖直方向有
水平方向有
A做匀速直线运动,有
P脱落瞬间滑轮到A左端距离为,则
则轻绳的长度
解得
(3)当P落在A右端时,速度最小,即
当P落在A左端时,速度最大,有,
解得
则A的速度满足
2.(1)
(2)
(3)0.75m
【详解】(1)对小球A受力分析,竖直方向上有
对小球B受力分析有
可得
(2)对小球A受力分析,水平方向上有
解得
(3)结合前面的分析有
解得
即小球A稳定转动时ω2与成反比,可知若小球A的角速度增大为原来的2倍,则重新稳定后小球A到上管口的绳长变为原来的,因此,重新稳定后小球B的高度变化量
3.(1)0.8m
(2)
(3)5.6N
【详解】(1)小球在竖直方向做自由落体运动
(2)小球到达点时竖直速度为,
则
(3)小球在轨道受到的支持力为,
所以
根据牛顿第三定律轨道受到的压力为
4.24cm/s2;4 cm/s2
【详解】AB两点的线速度大小相等,根据
可知
解得
AC两点角速度相同,则根据
可知
解得
5.(1)
(2)
【详解】(1)水在A点时的水平速度
水在B点时的速度
联立解得
(2)水在竖直方向上做匀加速直线运动,从A到B的竖直位移
而,
联立解得
6.(1)1:2:12
(2)1:1:6
(3)3.8m/s
(4)1:2:2
【详解】(1)链轮和飞轮边缘的线速度相等,根据
可知
后轮和飞轮的角速度相等,根据
可知
可知A、B、C三点的向心加速度大小之比是1:2:12;
(2)链轮和飞轮边缘的线速度相等,即vA=vB;
后轮和飞轮的角速度相等,根据
可知
可知A、B、C三点的线速度大小之比是1:1:6;
(3)链轮的角速度
则飞轮的角速度
自行车前进的速度即为后轮的线速度
(4)链轮和飞轮的角速度之比为
飞轮和后轮的角速度相等,即
可知链轮、飞轮和后轮的角速度大小之比为1:2:2。
7.(1)60cm
(2)3m/s
【详解】(1)设目标与迫击炮之间的距离为d,炮弹离开炮口时的速度大小为,炮筒与水平面之间的仰角为,炮弹的水平速度为
炮弹的竖直速度为
炮弹在空中飞行的时间
炮弹飞行的水平位移
联立可得
同理可得,当炮筒与水平面之间的仰角为时,炮弹飞行的水平位移
联立可得:
解得
(2)由以上分析可得
解得
8.(1)4m/s
(2)
(3),
【详解】(1)弹丸做平抛运动,水平方向上有
竖直方向上有
其中,
解得
(2)弹丸做平抛运动,有
弹丸落到P点时竖直方向上的分速度大小
弹丸击中P点时的速度大小
结合数学知识可知
即弹丸落到P点的最小速率
(3)弹丸做平抛运动,有,
弹丸垂直击中Q点时有
弹丸击中Q点时的速度大小
解得,
9.(1)0.4m
(2)60°
(3)0.23s
【详解】(1)机器猫在A板跳跃过程,系统水平动量守恒,得
解得A板运动的距离
猫运动的距离为
(2)设机器猫起跳速度为,A板获得的速度大小为
机器猫与A板水平方向动量守恒,有
机器猫的斜抛过程有
能量关系
联立可得
由数学关系可知当
即夹角为60°时W有最小值
(3)由
可得,
机器猫跳上B板,瞬间减速的过程中由动量定理
竖直方向上
水平方向上
联立可得 猫和B板瞬间碰撞后的速度分别为,
则
猫将在B板上匀减速滑行,B板将匀加速运动直至猫与B板共速(此时猫未滑下B板)
则有
可解得
联立可得
10.(1)
(2)
(3)5次
【详解】(1)根据题意可知,,
解得
(2)从M点到与木板B碰撞,由动能定理可得
解得
A与B发生弹性碰撞,有,
解得,
(3)因C与挡板间的碰撞为弹性碰撞,B和C系统动量守恒,最终B与C共速做匀速直线运动,故有
系统机械能损失为
系统损失的机械能转化为摩擦生热,有
解得
滑块C相对木板B上来回滑动的距离为3.5m,故C与左右两挡板碰撞的次数为
故滑块C与两侧挡板共碰撞5次。
答案第1页,共2页
答案第1页,共2页
1.如图所示,一不可伸长的轻绳跨过定滑轮分别连接木板A和小物块B(可看作质点),A的长度为,在水平地面上向右做速度大小为的匀速直线运动,B的下方悬有一水滴,与B一起在距离地面高处的水平光滑轨道上向左运动。当轻绳与水平方向夹角时,脱落,恰好落在A的右端。已知,滑轮可看做质点,不计A的厚度,不计空气阻力,取重力加速度大小,。求
(1)脱落时,B的速度大小;
(2)轻绳的长度;
(3)若使落在A上,A的速度应满足什么条件?
2.如图所示,不可伸长的轻绳穿过一竖直固定的光滑细管(半径可忽略),两端系有小球A、B(均可视为质点)。当小球A绕中心轴匀速转动时,小球B静止,小球A到上管口的绳长L=1m,与小球A相连的绳与竖直方向的夹角θ=60°。取重力加速度大小g=10m/s2,不计空气阻力。
(1)求小球A的质量m1与小球B的质量m2的比值;
(2)求小球A匀速转动的角速度大小ω;
(3)若小球A的角速度缓慢增大为原来的2倍,求重新稳定后小球B的高度变化量 h。
3.如图所示,将一质量为的小球自水平平台右端O点以一定的初速度水平抛出,小球飞离平台后经0.4s由A点沿切线落入竖直光滑圆轨道ABC,轨道半径,CB为其竖直直径。,。求:
(1)平台末端O点到A点的竖直高度H;
(2)小球到达A点的速度大小;
(3)小球在A点时对轨道的压力大小。
4.如图所示,压路机大轮的半径R是小轮半径r的2倍。压路机匀速行驶时,以压路机车架为参考系,大轮边缘上A点的向心加速度是12 cm/s2,那么小轮边缘上B点的向心加速度大小是多少?大轮上距轴心距离为的C点的向心加速度大小是多少?
5.图甲是消防车正在机场进行过水门仪式的情景。一名学生模拟消防水柱的示意图如图乙所示,水在空中运动,A、B为其运动轨迹上的两点,已知水在A点时的速度大小为,方向与竖直方向的夹角为;它运动到B点时,速度方向与竖直方向的夹角为。不计空气阻力,重力加速度g取。
试估算:
(1)水到达B点时的速度大小;
(2)A、B两点间的高度差。
6.如图所示为自行车的传动装置示意图,已知链轮的半径,飞轮的半径,后轮的半径,A、B、C(图中未画出)分别为链轮、飞轮和后轮边缘上的点。若脚蹬匀速转动一圈所需要的时间为,则在自行车匀速前进的过程中,求:
(1)A、B、C三点的向心加速度大小之比是多少?
(2)A、B、C三点的线速度大小之比是多少?
(3)自行车前进的速度大小约为多大?
(4)链轮、飞轮和后轮的角速度大小之比为多少?
7.如图所示为儿童迫击炮,在一次游戏活动中,某儿童用迫击炮轰击和炮在同一水平线上的目标。第一次发射时,炮筒与水平面之间的仰角为时,着弹点比目标近了一段距离;当第二次发射时,炮筒与水平面之间的仰角为时,着弹点比目标远了一段距离。已知炮弹每次离开炮口时的速度大小相等,重力加速度为g(g取),不计空气阻力,忽略炮口与目标之间的高度差。求:
(1)目标与迫击炮之间的距离d;
(2)炮弹离开炮口时的速度大小。
8.如图所示,足够长的竖直轨道AB与半圆槽BCD在同一竖直面内,O点为半圆槽的圆心,B、D点的连线水平,C为圆槽的最低点。安装在竖直轨道AB上的弹射器可上下移动,能水平向右发射出不同速率的弹丸(视为质点,出射点处于B点正上方)。已知半圆槽的半径R=3m,P点为半圆槽上O点右侧的一点,∠POD=θ=53°。取重力加速度大小g=10m/s2,sin53°=0.8,cos53°=0.6,不计空气阻力。
(1)调整弹射器的位置,使得弹丸出射点到B点的距离d1=4.8m,水平向右发射弹丸后弹丸恰好落在P点,求弹丸的初速度大小v1;
(2)调整弹射器的位置和弹丸的出射速率,使得弹丸均能击中半圆槽上的P点,求弹丸落到P点的最小速率vmin;
(3)调整弹射器的位置和弹丸的出射速率,使得弹丸垂直击中半圆槽上O点右侧的Q点(图中未画出),若已知弹丸击中Q点时的速度方向与水平方向的夹角为α(0<α<90°),求弹丸出射点到B点的距离d和弹丸击中Q点时的速度大小v。(均用α表示)
9.如图所示,质量均为M=9kg,厚度相同、长度均为L=0.6m的木板A、B(上表面粗糙)并排静止在光滑水平面上。质量m=18kg大小可忽略的机器猫静止于A板左端,机器描从A板左端斜向上跳出后,恰好落到A木板的右端,并立即与A板达到共速。随即以与第一次相同的速度起跳并落到B板上,机器猫落到B板上时碰撞时间极短可忽略,且不反弹。空气阻力可忽略,重力加速度为g=10m/s2。
(1)求从机器猫起跳至落在A板右端过程中A板运动的距离;
(2)求起跳速度与水平方向夹角为多少?可使机器猫起跳消耗的能量最少;
(3)新型材料制成的机器猫其质量仅为m′=7kg其他条件保持不变,机器猫总是以(2)问中的方式起跳,机器猫与B木板间的动摩擦因数为,求机器猫在B木板上的运动时间(结果保留两位小数)。
10.如图,MNP为一段光滑轨道,其中MN段是半径为的圆弧形轨道,M与圆心的连线与竖直方向夹角为53°。NP是水平足够长直轨道,MN与NP段在N点平滑连接。滑块A从距M点高度。处水平抛出,恰好能从M点切入轨道。在水平轨道某位置静止放置一长的木板B,木板左右两侧各有一固定挡板。木板紧靠右挡板放置一滑块C。滑块A在NP轨道上与木板B发生碰撞。若A、B、C三者质量相等,滑块A、C均可视为质点,A与B之间、C与挡板之间的碰撞均为弹性碰撞。B、C之间的动摩擦因数为,重力加速度,,,求:
(1)滑块A到达M点时的速度;
(2)滑块A与木板B碰后木板的速度;
(3)滑块C与左右两侧挡板碰撞的总次数。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.(1)
(2)
(3)
【详解】(1)木板A的速度大小等于小物块B沿轻绳方向的分速度
解得
(2)由几何知:P脱落瞬间B所在位置到滑轮间的轻绳距离
P脱落后做平抛运动,竖直方向有
水平方向有
A做匀速直线运动,有
P脱落瞬间滑轮到A左端距离为,则
则轻绳的长度
解得
(3)当P落在A右端时,速度最小,即
当P落在A左端时,速度最大,有,
解得
则A的速度满足
2.(1)
(2)
(3)0.75m
【详解】(1)对小球A受力分析,竖直方向上有
对小球B受力分析有
可得
(2)对小球A受力分析,水平方向上有
解得
(3)结合前面的分析有
解得
即小球A稳定转动时ω2与成反比,可知若小球A的角速度增大为原来的2倍,则重新稳定后小球A到上管口的绳长变为原来的,因此,重新稳定后小球B的高度变化量
3.(1)0.8m
(2)
(3)5.6N
【详解】(1)小球在竖直方向做自由落体运动
(2)小球到达点时竖直速度为,
则
(3)小球在轨道受到的支持力为,
所以
根据牛顿第三定律轨道受到的压力为
4.24cm/s2;4 cm/s2
【详解】AB两点的线速度大小相等,根据
可知
解得
AC两点角速度相同,则根据
可知
解得
5.(1)
(2)
【详解】(1)水在A点时的水平速度
水在B点时的速度
联立解得
(2)水在竖直方向上做匀加速直线运动,从A到B的竖直位移
而,
联立解得
6.(1)1:2:12
(2)1:1:6
(3)3.8m/s
(4)1:2:2
【详解】(1)链轮和飞轮边缘的线速度相等,根据
可知
后轮和飞轮的角速度相等,根据
可知
可知A、B、C三点的向心加速度大小之比是1:2:12;
(2)链轮和飞轮边缘的线速度相等,即vA=vB;
后轮和飞轮的角速度相等,根据
可知
可知A、B、C三点的线速度大小之比是1:1:6;
(3)链轮的角速度
则飞轮的角速度
自行车前进的速度即为后轮的线速度
(4)链轮和飞轮的角速度之比为
飞轮和后轮的角速度相等,即
可知链轮、飞轮和后轮的角速度大小之比为1:2:2。
7.(1)60cm
(2)3m/s
【详解】(1)设目标与迫击炮之间的距离为d,炮弹离开炮口时的速度大小为,炮筒与水平面之间的仰角为,炮弹的水平速度为
炮弹的竖直速度为
炮弹在空中飞行的时间
炮弹飞行的水平位移
联立可得
同理可得,当炮筒与水平面之间的仰角为时,炮弹飞行的水平位移
联立可得:
解得
(2)由以上分析可得
解得
8.(1)4m/s
(2)
(3),
【详解】(1)弹丸做平抛运动,水平方向上有
竖直方向上有
其中,
解得
(2)弹丸做平抛运动,有
弹丸落到P点时竖直方向上的分速度大小
弹丸击中P点时的速度大小
结合数学知识可知
即弹丸落到P点的最小速率
(3)弹丸做平抛运动,有,
弹丸垂直击中Q点时有
弹丸击中Q点时的速度大小
解得,
9.(1)0.4m
(2)60°
(3)0.23s
【详解】(1)机器猫在A板跳跃过程,系统水平动量守恒,得
解得A板运动的距离
猫运动的距离为
(2)设机器猫起跳速度为,A板获得的速度大小为
机器猫与A板水平方向动量守恒,有
机器猫的斜抛过程有
能量关系
联立可得
由数学关系可知当
即夹角为60°时W有最小值
(3)由
可得,
机器猫跳上B板,瞬间减速的过程中由动量定理
竖直方向上
水平方向上
联立可得 猫和B板瞬间碰撞后的速度分别为,
则
猫将在B板上匀减速滑行,B板将匀加速运动直至猫与B板共速(此时猫未滑下B板)
则有
可解得
联立可得
10.(1)
(2)
(3)5次
【详解】(1)根据题意可知,,
解得
(2)从M点到与木板B碰撞,由动能定理可得
解得
A与B发生弹性碰撞,有,
解得,
(3)因C与挡板间的碰撞为弹性碰撞,B和C系统动量守恒,最终B与C共速做匀速直线运动,故有
系统机械能损失为
系统损失的机械能转化为摩擦生热,有
解得
滑块C相对木板B上来回滑动的距离为3.5m,故C与左右两挡板碰撞的次数为
故滑块C与两侧挡板共碰撞5次。
答案第1页,共2页
答案第1页,共2页
同课章节目录
