数学:2.2《椭圆的几何性质(1)》课件(苏教版选修1-1)
文档属性
| 名称 | 数学:2.2《椭圆的几何性质(1)》课件(苏教版选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 191.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-25 00:00:00 | ||
图片预览



文档简介
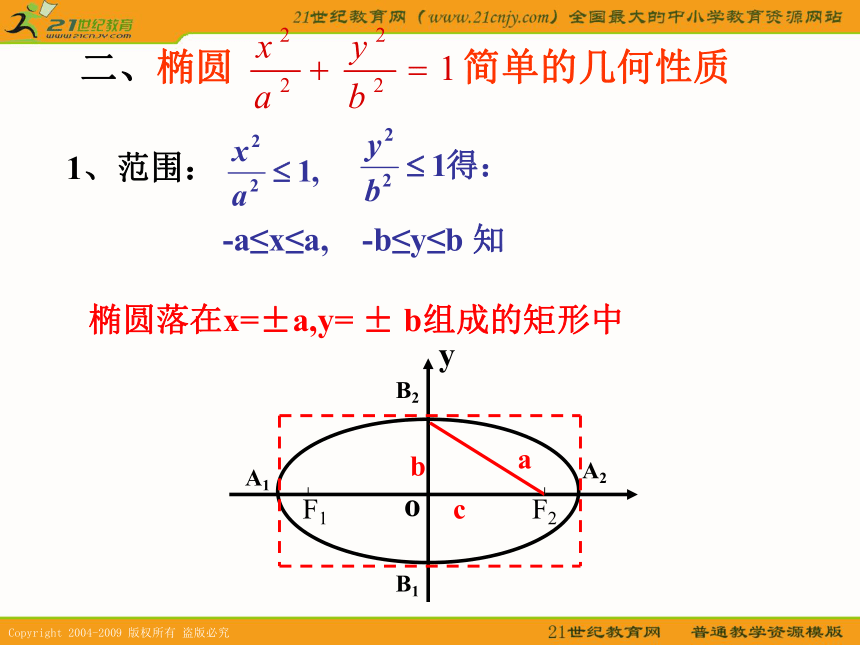
课件18张PPT。椭圆的简单几何性质(1)复习:1.椭圆的定义:到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2当焦点在X轴上时当焦点在Y轴上时二、椭圆 简单的几何性质 -a≤x≤a, -b≤y≤b 知
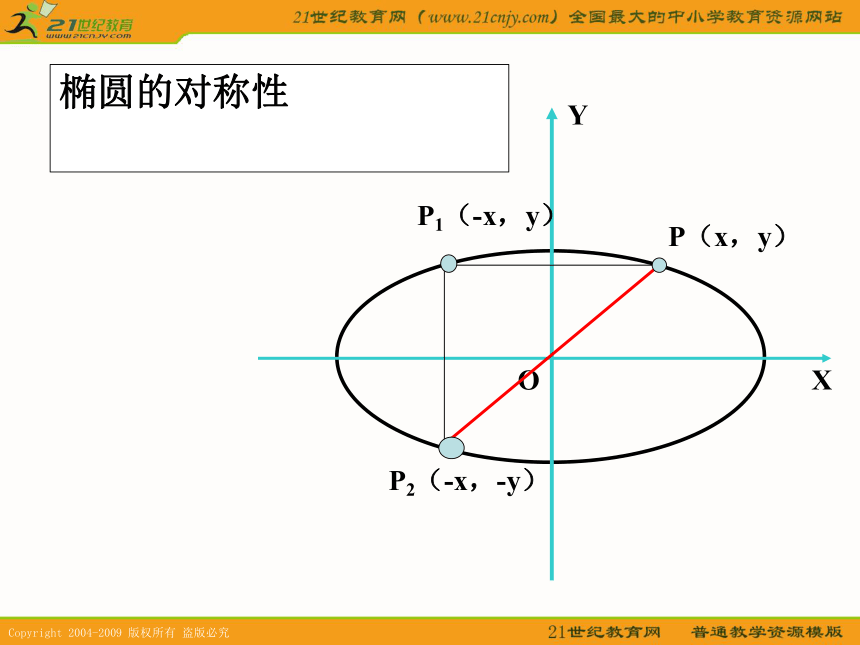
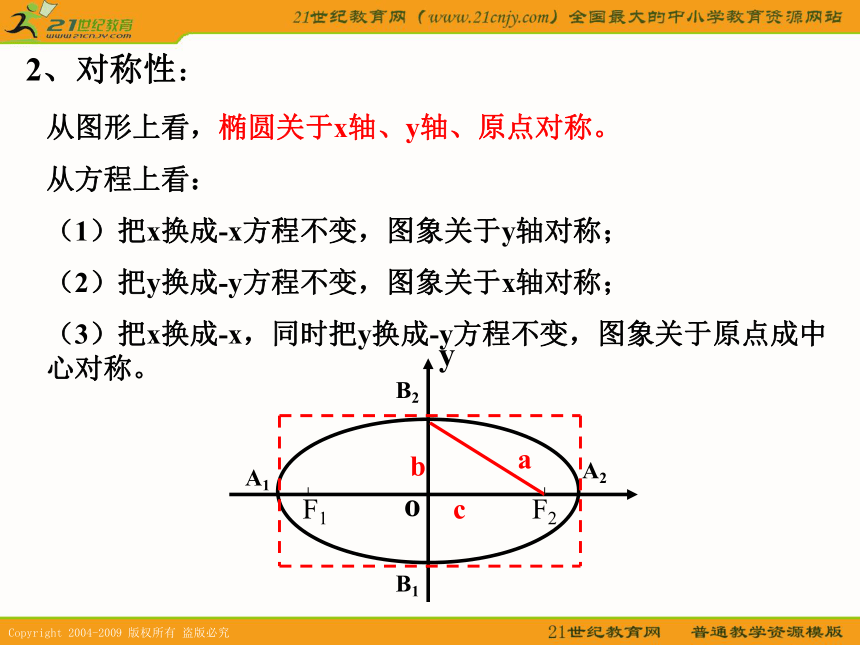
椭圆落在x=±a,y= ± b组成的矩形中1、范围:椭圆的对称性2、对称性:从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。3、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
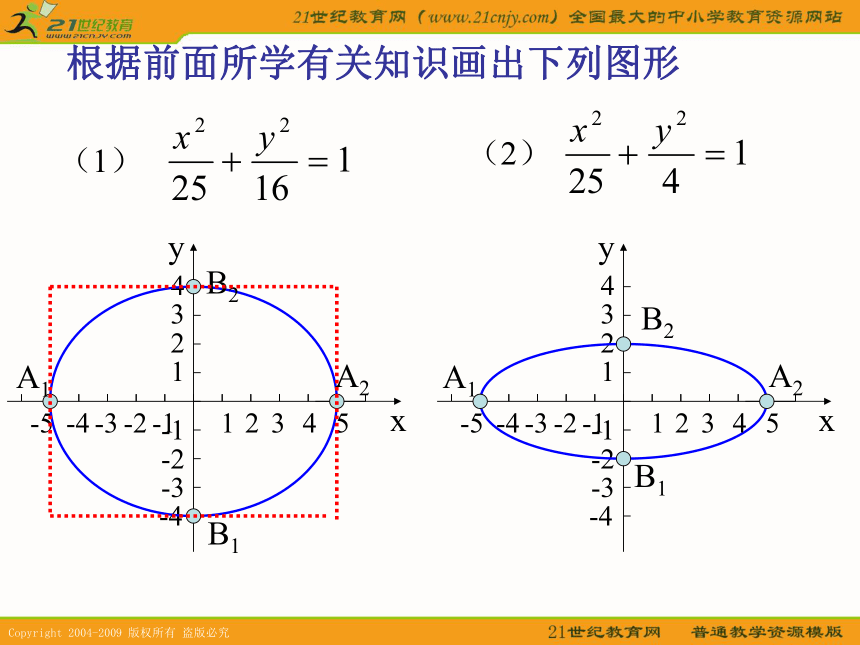
a、b分别叫做椭圆的长半轴长和短半轴长。根据前面所学有关知识画出下列图形(1)(2)A1 B1 A2 B2 B2 A2 B1 A1 4、椭圆的离心率e(刻画椭圆扁平程度的量)离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:[2]离心率对椭圆形状的影响:02)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆[3]e与a,b的关系:思考:当e=0时,曲线是什么?当e=1时曲 线又是 什么?|x|≤ a,|y|≤ b关于x轴、y轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ a,|y|≤ b关于x轴、y轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ b,|y|≤ a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0 , c)、(0, -c)同前同前同前例1已知椭圆方程为9x2+25y2=225, 它的长轴长是: 。短轴长是: 。
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 106860解题的关键:1、将椭圆方程转化为标准方程 明确a、b2、确定焦点的位置和长轴的位置练习:已知椭圆 的离心率
求m的值及椭圆的长轴和短轴的长、焦点坐
标、顶点坐标。练习
求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。
(1)x2+9y2=81 (2) 25x2+9y2=225
(3) 16x2+y2=25 (4) 4x2+5y2=1例2 求适合下列条件的椭圆的标准方程
⑴经过点P(-3,0)、Q(0,-2);
⑵长轴长等于20,离心率3/5。
⑶一焦点将长轴分成2:1的两部分,且经过点解: ⑴方法一:设方程为mx2+ny2=1(m>0,n>0,m≠n),将点的坐标方程,求出m=1/9,n=1/4。方法二:利用椭圆的几何性质,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点,于是焦点在x轴上,且点P、Q分别是椭圆长轴与短轴的一个端点
,故a=3,b=2,所以椭圆的标准方程为 注:待定系数法求椭圆标准方程的步骤: ⑴定位; ⑵定量⑶⑵或 或练习:
1. 根据下列条件,求椭圆的标准方程。
① 长轴长和短轴长分别为8和6,焦点在x轴上
② 长轴和短轴分别在y轴,x轴上,经过P(-2,0),
Q(0,-3)两点.
③一焦点坐标为(-3,0)一顶点坐标为(0,5)
④两顶点坐标为(0,±6),且经过点(5,4)
⑤焦距是12,离心率是0.6,焦点在x轴上。2. 已知椭圆的一个焦点为F(6,0)点B,C是短轴的两端点,△FBC是等边三角形,求这个椭圆的标准方程。例3:(1)椭圆 的左焦点
是两个顶点,如果到直线AB的距
离为 ,则椭圆的离心率e= .
(3)设M为椭圆 上一点, 为椭圆的焦点,
如果 ,求椭圆的离心率。小结:本节课我们学习了椭圆的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义。了解了研究椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系,这对我们解决椭圆中的相关问题有很大的帮助,给我们以后学习圆锥曲线其他的两种曲线扎实了基础。在解析几何的学习中,我们更多的是从方程的形式这个角度来挖掘题目中的隐含条件,需要我们认识并熟练掌握数与形的联系。在本节课中,我们运用了几何性质,待定系数法来求解椭圆方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想。 (4)P为椭圆 上任意一点,F1、F2是焦点,
则∠F1PF2的最大值是 .
椭圆落在x=±a,y= ± b组成的矩形中1、范围:椭圆的对称性2、对称性:从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。3、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。根据前面所学有关知识画出下列图形(1)(2)A1 B1 A2 B2 B2 A2 B1 A1 4、椭圆的离心率e(刻画椭圆扁平程度的量)离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:[2]离心率对椭圆形状的影响:0
焦距是: 。 离心率等于: 。
焦点坐标是: 。顶点坐标是: 。
外切矩形的面积等于: 。 106860解题的关键:1、将椭圆方程转化为标准方程 明确a、b2、确定焦点的位置和长轴的位置练习:已知椭圆 的离心率
求m的值及椭圆的长轴和短轴的长、焦点坐
标、顶点坐标。练习
求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。
(1)x2+9y2=81 (2) 25x2+9y2=225
(3) 16x2+y2=25 (4) 4x2+5y2=1例2 求适合下列条件的椭圆的标准方程
⑴经过点P(-3,0)、Q(0,-2);
⑵长轴长等于20,离心率3/5。
⑶一焦点将长轴分成2:1的两部分,且经过点解: ⑴方法一:设方程为mx2+ny2=1(m>0,n>0,m≠n),将点的坐标方程,求出m=1/9,n=1/4。方法二:利用椭圆的几何性质,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点,于是焦点在x轴上,且点P、Q分别是椭圆长轴与短轴的一个端点
,故a=3,b=2,所以椭圆的标准方程为 注:待定系数法求椭圆标准方程的步骤: ⑴定位; ⑵定量⑶⑵或 或练习:
1. 根据下列条件,求椭圆的标准方程。
① 长轴长和短轴长分别为8和6,焦点在x轴上
② 长轴和短轴分别在y轴,x轴上,经过P(-2,0),
Q(0,-3)两点.
③一焦点坐标为(-3,0)一顶点坐标为(0,5)
④两顶点坐标为(0,±6),且经过点(5,4)
⑤焦距是12,离心率是0.6,焦点在x轴上。2. 已知椭圆的一个焦点为F(6,0)点B,C是短轴的两端点,△FBC是等边三角形,求这个椭圆的标准方程。例3:(1)椭圆 的左焦点
是两个顶点,如果到直线AB的距
离为 ,则椭圆的离心率e= .
(3)设M为椭圆 上一点, 为椭圆的焦点,
如果 ,求椭圆的离心率。小结:本节课我们学习了椭圆的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义。了解了研究椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系,这对我们解决椭圆中的相关问题有很大的帮助,给我们以后学习圆锥曲线其他的两种曲线扎实了基础。在解析几何的学习中,我们更多的是从方程的形式这个角度来挖掘题目中的隐含条件,需要我们认识并熟练掌握数与形的联系。在本节课中,我们运用了几何性质,待定系数法来求解椭圆方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想。 (4)P为椭圆 上任意一点,F1、F2是焦点,
则∠F1PF2的最大值是 .
