数学:2.2《椭圆的几何性质(2)》课件(苏教版选修1-1)
文档属性
| 名称 | 数学:2.2《椭圆的几何性质(2)》课件(苏教版选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-25 00:00:00 | ||
图片预览






文档简介
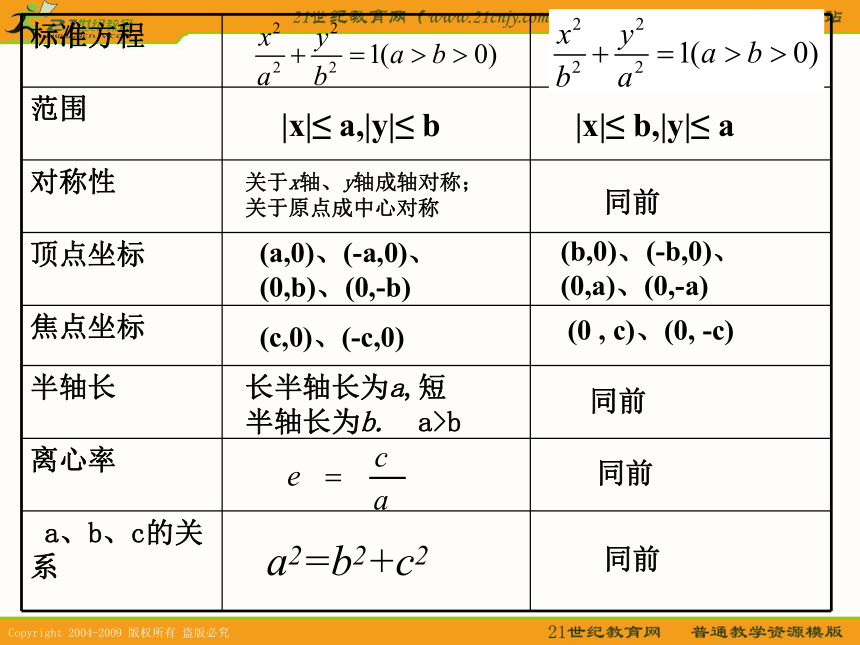
课件15张PPT。2.2.2椭圆的简单几何性质(2)|x|≤ a,|y|≤ b关于x轴、y轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ b,|y|≤ a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0 , c)、(0, -c)同前同前同前复习练习:
1.椭圆的长短轴之和为18,焦距为6,则椭圆的标准方程为( )2、下列方程所表示的曲线中,关于x轴和y 轴
都对称的是( )
A、X2=4Y B、X2+2XY+Y=0 C、X2-4Y2=X
D、9X2+Y2=4CD练习1、若椭圆的焦距长等于它的短轴长,则其离心率为 。
2、若椭圆的两个焦点及一个短轴端点构成正三角形,则其离心率为 。
3、若椭圆的 的两个焦点把长轴分成三等分,则其离心率为 。4、若某个椭圆的长轴、短轴、焦距依次成等差数列,
则其离心率e=__________(±a,0)a(0, ±b)b(-a,0)a+c(a,0)a-c6、5、以椭圆的焦距为直径并过两焦点的圆,交椭圆于四个不同的点,顺次连接这四个点和两个焦点恰好组成一个正六边形,那么这个椭圆的离心率 。例1 如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆,已知它的近地点A(离地面最近的点)距地面439km,远地点B距地面2384km.并且F2、A、B在同一直线上,地球半径约为6371km,求卫星运行的轨道方程(精确到1km).XOF1F2ABXXY解:以直线AB为x轴,线段AB的中垂线为y轴建立如图所示的直角坐标系,AB与地球交与C,D两点。由题意知:|AC|=439,|BD|=2384,DC∴b≈7722.2、2005年10月17日,神州六号载人飞船带着亿万中华儿女千万年的梦想与希望,遨游太空返回地面。其运行的轨道是以地球中心为一焦点的椭圆,设其近地点距地面m(km),远地点距地面n(km),地球半径R(km),则载人飞船运行轨道的短轴长为( )A. mn(km) B. 2mn(km)DHd思考上面探究问题,并回答下列问题:探究:(1)用坐标法如何求出其轨迹方程,并说出轨迹(2)给椭圆下一个新的定义归纳:椭圆的第一定义与第二定义是相呼应的。练 习 (a>b>0)左焦点为F1,右焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ex0,|PF2|=a-ex0。其中|PF1|、 |PF2|叫焦半径. (a>b>0)下焦点为F1,上焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ey0,|PF2|=a-ey0。其中|PF1|、 |PF2|叫焦半径.说明:练习:已知椭圆 P为椭圆在第一象限内的点,它
与两焦点的连线互相垂直,求P点的坐标。法二定义:注:我们一般把这个定义称为椭圆的第二定义,而相应的把另一个定义称为椭圆的第一定义。定点是椭圆的焦点,定直线叫做椭圆的准线。
1.椭圆的长短轴之和为18,焦距为6,则椭圆的标准方程为( )2、下列方程所表示的曲线中,关于x轴和y 轴
都对称的是( )
A、X2=4Y B、X2+2XY+Y=0 C、X2-4Y2=X
D、9X2+Y2=4CD练习1、若椭圆的焦距长等于它的短轴长,则其离心率为 。
2、若椭圆的两个焦点及一个短轴端点构成正三角形,则其离心率为 。
3、若椭圆的 的两个焦点把长轴分成三等分,则其离心率为 。4、若某个椭圆的长轴、短轴、焦距依次成等差数列,
则其离心率e=__________(±a,0)a(0, ±b)b(-a,0)a+c(a,0)a-c6、5、以椭圆的焦距为直径并过两焦点的圆,交椭圆于四个不同的点,顺次连接这四个点和两个焦点恰好组成一个正六边形,那么这个椭圆的离心率 。例1 如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆,已知它的近地点A(离地面最近的点)距地面439km,远地点B距地面2384km.并且F2、A、B在同一直线上,地球半径约为6371km,求卫星运行的轨道方程(精确到1km).XOF1F2ABXXY解:以直线AB为x轴,线段AB的中垂线为y轴建立如图所示的直角坐标系,AB与地球交与C,D两点。由题意知:|AC|=439,|BD|=2384,DC∴b≈7722.2、2005年10月17日,神州六号载人飞船带着亿万中华儿女千万年的梦想与希望,遨游太空返回地面。其运行的轨道是以地球中心为一焦点的椭圆,设其近地点距地面m(km),远地点距地面n(km),地球半径R(km),则载人飞船运行轨道的短轴长为( )A. mn(km) B. 2mn(km)DHd思考上面探究问题,并回答下列问题:探究:(1)用坐标法如何求出其轨迹方程,并说出轨迹(2)给椭圆下一个新的定义归纳:椭圆的第一定义与第二定义是相呼应的。练 习 (a>b>0)左焦点为F1,右焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ex0,|PF2|=a-ex0。其中|PF1|、 |PF2|叫焦半径. (a>b>0)下焦点为F1,上焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ey0,|PF2|=a-ey0。其中|PF1|、 |PF2|叫焦半径.说明:练习:已知椭圆 P为椭圆在第一象限内的点,它
与两焦点的连线互相垂直,求P点的坐标。法二定义:注:我们一般把这个定义称为椭圆的第二定义,而相应的把另一个定义称为椭圆的第一定义。定点是椭圆的焦点,定直线叫做椭圆的准线。
