【新教材新课标】苏科版数学八年级上册1.5等腰三角形(第2课时等腰三角形的判定)课件(共18张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.5等腰三角形(第2课时等腰三角形的判定)课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 41.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:43:10 | ||
图片预览



文档简介
(共18张PPT)
1.5 等腰三角形
第2课时 等腰三角形的判定
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
经历等腰三角形判定的探究过程,体验研究几何图形的基本过程.
掌握等腰三角形的判定定理,并能应用它们进行计算和证明,发展推理能力.
问题引入
我们知道,等腰三角形的两底角相等.反过来,有两个角相等的三角形一定是等腰三角形吗?
?
?
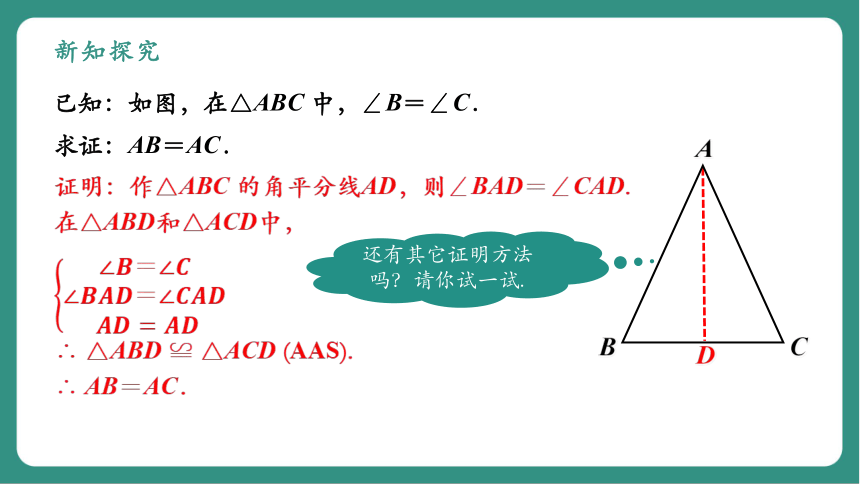
新知探究
已知:如图,在△ABC 中,∠B=∠C.
求证:AB=AC.
证明:作△ABC 的角平分线AD,则∠BAD=∠CAD.
在△ABD和△ACD中,
∴ △ABD ≌ △ACD (AAS).
∴ AB=AC.
B
C
A
D
还有其它证明方法吗?请你试一试.
新知探究
已知:如图,在△ABC 中,∠B=∠C.
求证:AB=AC.
证明:作边BC的高线AD,则∠ADB=∠ADC=90°.
在△ABD和△ACD中,
∴ △ABD ≌ △ACD (AAS).
∴ AB=AC.
B
C
A
D
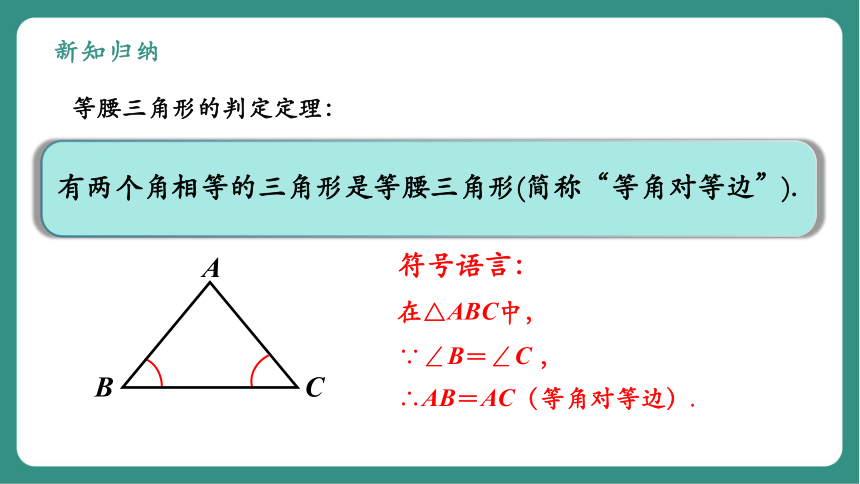
新知归纳
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
等腰三角形的判定定理:
A
B
C
在△ABC中,
∵∠B=∠C ,
∴AB=AC(等角对等边).
符号语言:
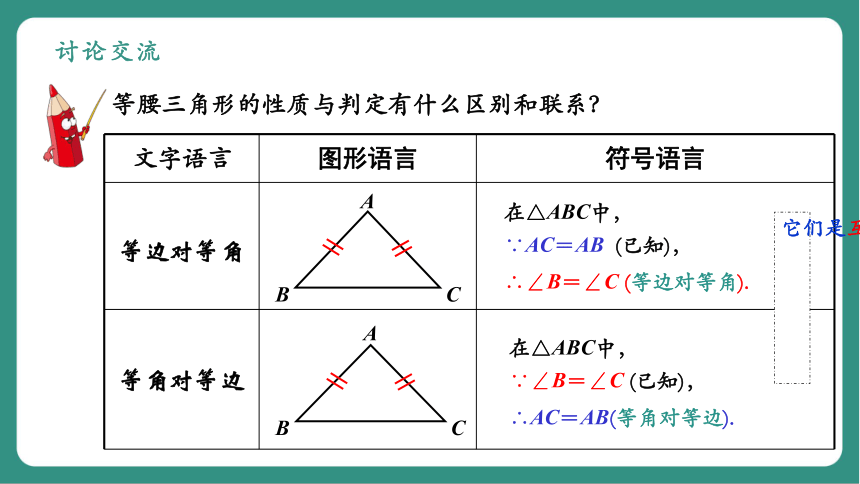
讨论交流
等腰三角形的性质与判定有什么区别和联系?
文字语言 图形语言 符号语言
等边对等角
等角对等边
∴∠B=∠C (等边对等角).
A
B
C
在△ABC中,
∵AC=AB (已知),
∴AC=AB(等角对等边).
A
B
C
在△ABC中,
∵∠B=∠C (已知),
它们是互逆命题.
典例分析
例 如图,∠EAC是△ABC的外角,AD平分∠EAC,AD∥BC.
求证:AB=AC.
A
B
C
D
E
证明:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C.
∵AD平分∠EAC,
∴∠EAD=∠DAC.
∴∠B=∠C.
∴ AB=AC(等角对等边).
典例分析
变式1 如图,如果AB=AC,AD∥BC,那么AD平分∠EAC吗?请证明你的结论.
A
B
C
D
E
证明:∵AB=AC,
∴∠B=∠C.
∵ AD∥BC,
∴∠EAD=∠B,∠DAC=∠C.
∴∠EAD=∠DAC.
∴AD平分∠EAC.
归纳总结
变式2 已知:如图,在△ABC中,AD平分∠BAC,DE∥AC.
求证:△ADE是等腰三角形.
A
B
C
D
E
证明:∵DE∥AC,
∴∠ADE=∠DAC.
∵AD平分∠BAC,
∴∠BAD=∠DAC.
∴∠ADE=∠BAD.
∴ EA=ED,
∴ △ADE是等腰三角形.
探究思考
当△ABC分别满足下列条件时,试在其一边上找到一点P,使点P与△ABC的两个顶点构成等腰三角形.
(1)等腰三角形; (2)直角三角形; (3)钝角三角形.
P
A
B
C
(1)
P
C
B
A
(3)
P
C
B
A
(2)
解:如图所示,△BPC即为所求.
新知巩固
1. 如图,AC=BC,∠B=72°,AD平分∠BAC,请写出图中的等腰三角形.
D
A
B
C
解:∵AC=BC,∴△ABC是等腰三角形.
∵AC=BC,∠B=72°,
∴∠BAC=∠B=72°,
∴∠C=180°-(72°+72°)=36°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=36°.
∴∠CAD=∠C.
∴AD=CD,
∴△CAD为等腰三角形.
∵∠BDA=∠C+∠CAD=72°,
∴∠BDA=∠B,
∴AB=AD.
∴△BAD为等腰三角形.
新知巩固
变式 如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有_____个.
5
A
B
C
E
D
新知巩固
2. 如图(1),在一张长方形纸片上任意画一条线段AB,将纸片沿线段AB折叠[图(2)]. 重叠部分的△ABC是等腰三角形吗?证明你的结论.
A
B
A
B
(1)
(2)
解:重叠部分的△ABC是等腰三角形.
因为图(1)中,长方形纸片的上、下两边平行,
所以∠1=∠2.
因为沿线段AB折叠纸片,∠1、∠2是重叠部分的
△ABC的内角(如图(2)).
所以依据“等角对等边”得AC=BC.
所以△ABC是等腰三角形.
1
2
1
2
C
新知巩固
3. 如图,在△ABC中,AB=AC,角平分线BD、CE相交于点O. OB与OC相等吗?请说明理由.
A
B
C
O
E
D
解:OB=OC.理由如下:
∵AB=AC,
∴∠ABC=∠ACB .
∵BD、CE是角平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB .
∴∠OBC=∠OCB .
∴OB=OC .
新知巩固
4.已知:如图,在△ABC中,DE=DF,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:△ABC是等腰三角形.
D
A
B
C
F
E
证明:∵ D是BC的中点,
∴ DB=DC.
∵ DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL).
∴∠B=∠C,
∴AB=AC.
课堂小结
等腰三角形的判定
内容
基本模型
等角对等边
角平分线+平行线 → 等腰三角形
等腰三角形+平行线 → 角平分线
感谢聆听!
1.5 等腰三角形
第2课时 等腰三角形的判定
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
经历等腰三角形判定的探究过程,体验研究几何图形的基本过程.
掌握等腰三角形的判定定理,并能应用它们进行计算和证明,发展推理能力.
问题引入
我们知道,等腰三角形的两底角相等.反过来,有两个角相等的三角形一定是等腰三角形吗?
?
?
新知探究
已知:如图,在△ABC 中,∠B=∠C.
求证:AB=AC.
证明:作△ABC 的角平分线AD,则∠BAD=∠CAD.
在△ABD和△ACD中,
∴ △ABD ≌ △ACD (AAS).
∴ AB=AC.
B
C
A
D
还有其它证明方法吗?请你试一试.
新知探究
已知:如图,在△ABC 中,∠B=∠C.
求证:AB=AC.
证明:作边BC的高线AD,则∠ADB=∠ADC=90°.
在△ABD和△ACD中,
∴ △ABD ≌ △ACD (AAS).
∴ AB=AC.
B
C
A
D
新知归纳
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
等腰三角形的判定定理:
A
B
C
在△ABC中,
∵∠B=∠C ,
∴AB=AC(等角对等边).
符号语言:
讨论交流
等腰三角形的性质与判定有什么区别和联系?
文字语言 图形语言 符号语言
等边对等角
等角对等边
∴∠B=∠C (等边对等角).
A
B
C
在△ABC中,
∵AC=AB (已知),
∴AC=AB(等角对等边).
A
B
C
在△ABC中,
∵∠B=∠C (已知),
它们是互逆命题.
典例分析
例 如图,∠EAC是△ABC的外角,AD平分∠EAC,AD∥BC.
求证:AB=AC.
A
B
C
D
E
证明:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C.
∵AD平分∠EAC,
∴∠EAD=∠DAC.
∴∠B=∠C.
∴ AB=AC(等角对等边).
典例分析
变式1 如图,如果AB=AC,AD∥BC,那么AD平分∠EAC吗?请证明你的结论.
A
B
C
D
E
证明:∵AB=AC,
∴∠B=∠C.
∵ AD∥BC,
∴∠EAD=∠B,∠DAC=∠C.
∴∠EAD=∠DAC.
∴AD平分∠EAC.
归纳总结
变式2 已知:如图,在△ABC中,AD平分∠BAC,DE∥AC.
求证:△ADE是等腰三角形.
A
B
C
D
E
证明:∵DE∥AC,
∴∠ADE=∠DAC.
∵AD平分∠BAC,
∴∠BAD=∠DAC.
∴∠ADE=∠BAD.
∴ EA=ED,
∴ △ADE是等腰三角形.
探究思考
当△ABC分别满足下列条件时,试在其一边上找到一点P,使点P与△ABC的两个顶点构成等腰三角形.
(1)等腰三角形; (2)直角三角形; (3)钝角三角形.
P
A
B
C
(1)
P
C
B
A
(3)
P
C
B
A
(2)
解:如图所示,△BPC即为所求.
新知巩固
1. 如图,AC=BC,∠B=72°,AD平分∠BAC,请写出图中的等腰三角形.
D
A
B
C
解:∵AC=BC,∴△ABC是等腰三角形.
∵AC=BC,∠B=72°,
∴∠BAC=∠B=72°,
∴∠C=180°-(72°+72°)=36°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=36°.
∴∠CAD=∠C.
∴AD=CD,
∴△CAD为等腰三角形.
∵∠BDA=∠C+∠CAD=72°,
∴∠BDA=∠B,
∴AB=AD.
∴△BAD为等腰三角形.
新知巩固
变式 如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有_____个.
5
A
B
C
E
D
新知巩固
2. 如图(1),在一张长方形纸片上任意画一条线段AB,将纸片沿线段AB折叠[图(2)]. 重叠部分的△ABC是等腰三角形吗?证明你的结论.
A
B
A
B
(1)
(2)
解:重叠部分的△ABC是等腰三角形.
因为图(1)中,长方形纸片的上、下两边平行,
所以∠1=∠2.
因为沿线段AB折叠纸片,∠1、∠2是重叠部分的
△ABC的内角(如图(2)).
所以依据“等角对等边”得AC=BC.
所以△ABC是等腰三角形.
1
2
1
2
C
新知巩固
3. 如图,在△ABC中,AB=AC,角平分线BD、CE相交于点O. OB与OC相等吗?请说明理由.
A
B
C
O
E
D
解:OB=OC.理由如下:
∵AB=AC,
∴∠ABC=∠ACB .
∵BD、CE是角平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB .
∴∠OBC=∠OCB .
∴OB=OC .
新知巩固
4.已知:如图,在△ABC中,DE=DF,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:△ABC是等腰三角形.
D
A
B
C
F
E
证明:∵ D是BC的中点,
∴ DB=DC.
∵ DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL).
∴∠B=∠C,
∴AB=AC.
课堂小结
等腰三角形的判定
内容
基本模型
等角对等边
角平分线+平行线 → 等腰三角形
等腰三角形+平行线 → 角平分线
感谢聆听!
同课章节目录
