【新教材新课标】苏科版数学八年级上册1.5等腰三角形(第1课时等腰三角形的性质)课件(共26张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.5等腰三角形(第1课时等腰三角形的性质)课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 45.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:42:18 | ||
图片预览


文档简介
(共26张PPT)
1.5 等腰三角形
第1课时 等腰三角形的性质
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历等腰三角形性质的探究过程,体验研究几何图形的基本过程.
掌握等腰三角形的性质定理,并能应用它们进行计算和证明,发展推理能力.
3. 会利用基本作图作三角形:已知底边及底边上的高作等腰三角形.
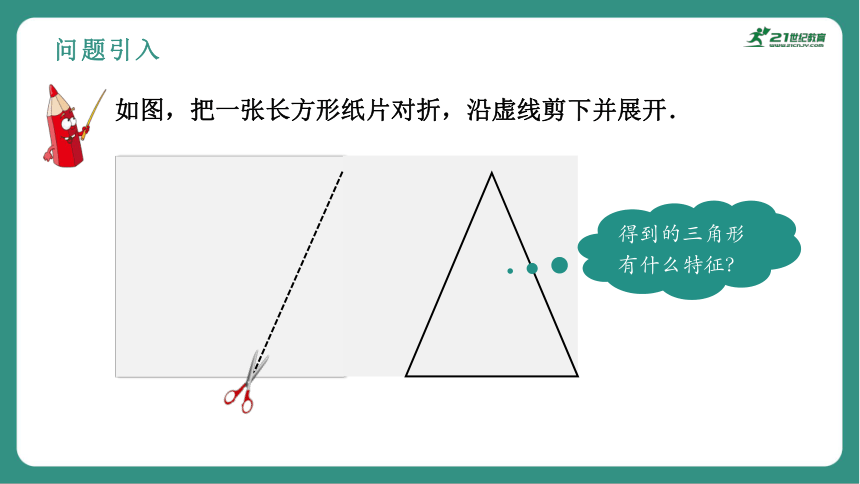
问题引入
如图,把一张长方形纸片对折,沿虚线剪下并展开.
得到的三角形有什么特征?
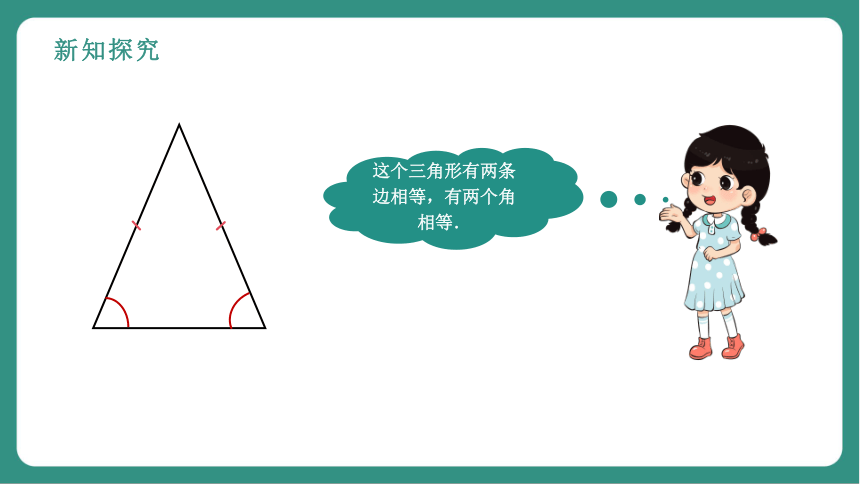
新知探究
这个三角形有两条边相等,有两个角相等.
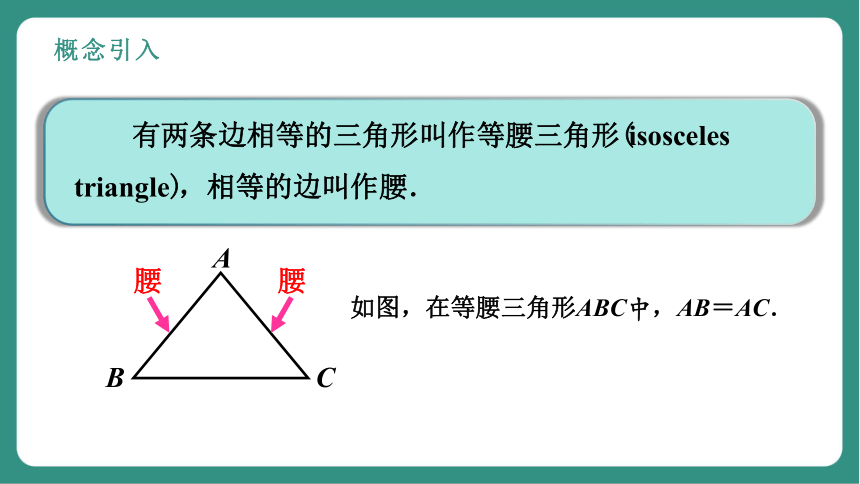
概念引入
有两条边相等的三角形叫作等腰三角形(isosceles triangle),相等的边叫作腰.
A
B
C
腰
腰
如图,在等腰三角形ABC中,AB=AC.
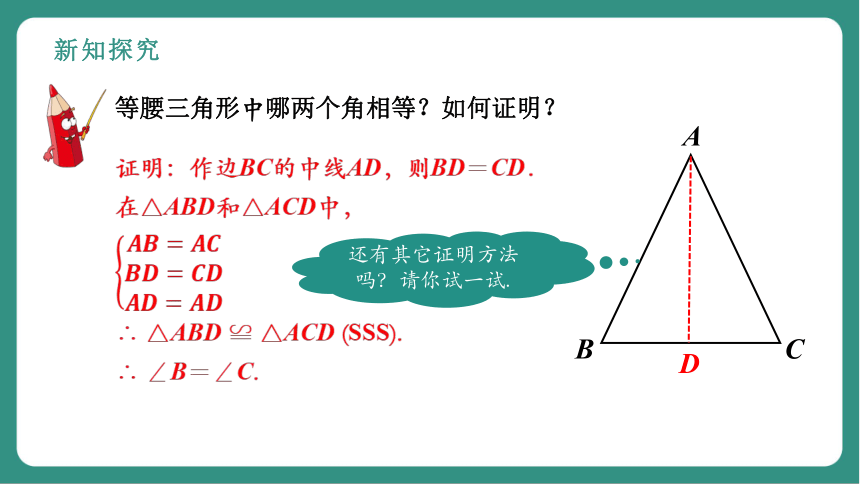
新知探究
A
B
C
D
等腰三角形中哪两个角相等?如何证明?
证明:作边BC的中线AD,则BD=CD.
在△ABD和△ACD中,
∴ △ABD ≌ △ACD (SSS).
∴ ∠B=∠C.
还有其它证明方法吗?请你试一试.
新知探究
A
B
C
D
等腰三角形中哪两个角相等?如何证明?
证明:作边BC的高线AD,
则∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
∴ Rt△ABD ≌ Rt△ACD (SSS).
∴ ∠B=∠C.
新知探究
A
B
C
D
等腰三角形中哪两个角相等?如何证明?
证明:作∠BAC的平分线AD,则∠BAD=∠CAD.
在△BAD和△CAD中,
∴ △BAD ≌ △CAD (SAS).
∴ ∠B=∠C.
新知探究
A
B
C
D
等腰三角形中哪两个角相等?如何证明?
也可以用等腰三角形的对称性证明.
概念引入
等腰三角形中两个相等的角叫作底角.
A
B
C
底角
底角
新知归纳
等腰三角形的两底角相等(简称“等边对等角”).
等腰三角形的性质定理1:
A
B
C
在△ABC中,
∵AB=AC,
∴∠B=∠C (等边对等角).
符号语言:
新知探究
A
B
C
D
由以上证明过程,你还有什么发现?
由以上证明可得,
△ABD≌△ACD,
∴∠BAD=∠CAD,
即AD是△ABC的角平分线.
由△ABD≌△ACD,
∴∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.
∴AD⊥BC,即AD是△ABC的高.
新知归纳
等腰三角形底边上的高线、中线及顶角平分线重合
(简称“三线合一”).
等腰三角形的性质定理2:
注意:应用“三线合一”的前提条件:
一是等腰三角形;二是三线中要具备一线.
归纳总结
在△ABC中,AB=AC.
(1)∵AD⊥BC,∴AD平分∠BAC,且BD=CD;
(2)∵BD=CD,∴AD平分∠BAC,且AD⊥BC;
(3)∵AD平分∠BAC,∴BD=CD,且AD⊥BC.
A
B
C
D
符号语言:
记忆口诀:一顶三线合.
前提条件
三线中要具备一线
典例分析
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,求证:∠ADB=∠BAC.
A
B
C
D
要证∠ADB=∠BAC
只要找与∠1相等且与∠C也相等的角.
由于∠BAC=∠1+∠2,
∠ADB=∠C+∠2.
只要证∠1=∠C
怎么想
怎么写
?
?
典例分析
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,求证:∠ADB=∠BAC.
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠BAD=∠B(等边对等角)
∴∠C=∠BAD.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠CAD.
∴∠ADB=∠BAD+∠CAD.
∴∠ADB=∠BAC.
A
B
C
D
?
?
典例分析
变式 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
求∠BAC的度数.
解:设∠B=x°.
∵AD=BD,
∴∠BAD=∠B=x°.
∴∠ADC=∠BAD+∠B=(2x)°.
∵DC=AC,
∴∠DAC=∠ADC=(2x)°.
∵AB=AC,
∴∠C=∠B=x°.
∵∠C+∠DAC+∠ADC=180°,
∴x+2x+2x=180.
∴x=36,即∠B=36°.
∴∠BAC=180°-36°-36°=108°.
A
B
C
D
典例分析
例2 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
A
C
B
E
D
图①
G
证明:(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE.
典例分析
例2 已知点D、E在△ABC的边BC上,AB=AC.
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
A
F
C
B
E
D
图②
证明:(2)∵F为DE的中点,
∴DF=EF.
∵BD=CE,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
尝试交流
如图,已知线段a,h,用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.
a
h
作法:
1.作线段BC=a.
2.作线段BC的垂直平分线MN,MN交BC于点D.
3.在MN上截取线段DA,使AD=h.
4.连接AB、AC.
△ABC就是所求作的等腰三角形.
a
M
N
A
●
B
●
●
C
h
●
D
新知巩固
1.在△ABC中,AB=AC.
(1)如果有一个角等于120°,那么∠A=____°,∠B=____°,
∠C=____°;
(2)如果有一个角等于50°,那么另两个角分别等于多少度?
120
30
30
解:如果有一个角等于50°,有以下两种情况:
①当∠A=50°时,∠B=∠C=(180°-∠A)=(180°-50°)=65°.
②当∠B=50°时,∠C=∠B=50°,
∠A=180°-(∠B+∠C) =180°-(50°+50°)=80°.
新知巩固
2.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC,
∴ AD⊥BC.
1
2
解: (1) ∵AB=AC,BD=DC,
∴∠1=∠2=∠BAC.
∵∠BAC=110°,
∴∠1=∠2=55°.
新知巩固
3.如图,AB=AD,CB=CD,连接AC,BD.
求证:AC⊥BD.
C
B
A
D
证明:∵AB=AD,CB=CD,
∴点A、C在BD的垂直平分线上.
∴ AC垂直平分BD,
∴ AC⊥BD.
新知巩固
4.已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:DE=DF.
D
A
B
C
F
E
证明:连接AD.
∵ AB=AC,D是BC的中点,
∴ AD平分∠BAC.
∵ DE⊥AB,DF⊥AC,
∴ DE=DF.
等腰三角形底边中点到两腰的距离相等.
课堂小结
等腰三角形
定义
性质
有两条边相等的三角形叫作等腰三角形.相等的边叫作腰.
等边对等角
三线合一
等腰三角形底边上的高线、中线及顶角平分线重合.
常用辅助线:作顶角平分线、底边上的高、底边上的中线是常见的辅助线.
感谢聆听!
1.5 等腰三角形
第1课时 等腰三角形的性质
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历等腰三角形性质的探究过程,体验研究几何图形的基本过程.
掌握等腰三角形的性质定理,并能应用它们进行计算和证明,发展推理能力.
3. 会利用基本作图作三角形:已知底边及底边上的高作等腰三角形.
问题引入
如图,把一张长方形纸片对折,沿虚线剪下并展开.
得到的三角形有什么特征?
新知探究
这个三角形有两条边相等,有两个角相等.
概念引入
有两条边相等的三角形叫作等腰三角形(isosceles triangle),相等的边叫作腰.
A
B
C
腰
腰
如图,在等腰三角形ABC中,AB=AC.
新知探究
A
B
C
D
等腰三角形中哪两个角相等?如何证明?
证明:作边BC的中线AD,则BD=CD.
在△ABD和△ACD中,
∴ △ABD ≌ △ACD (SSS).
∴ ∠B=∠C.
还有其它证明方法吗?请你试一试.
新知探究
A
B
C
D
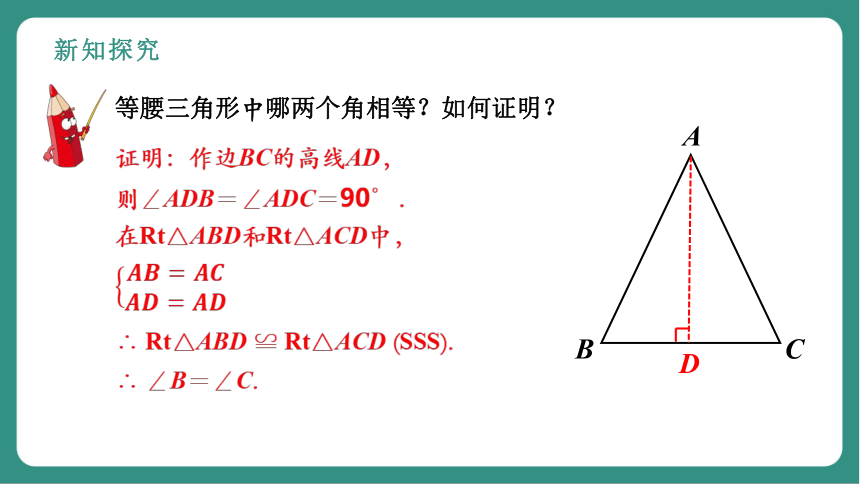
等腰三角形中哪两个角相等?如何证明?
证明:作边BC的高线AD,
则∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
∴ Rt△ABD ≌ Rt△ACD (SSS).
∴ ∠B=∠C.
新知探究
A
B
C
D
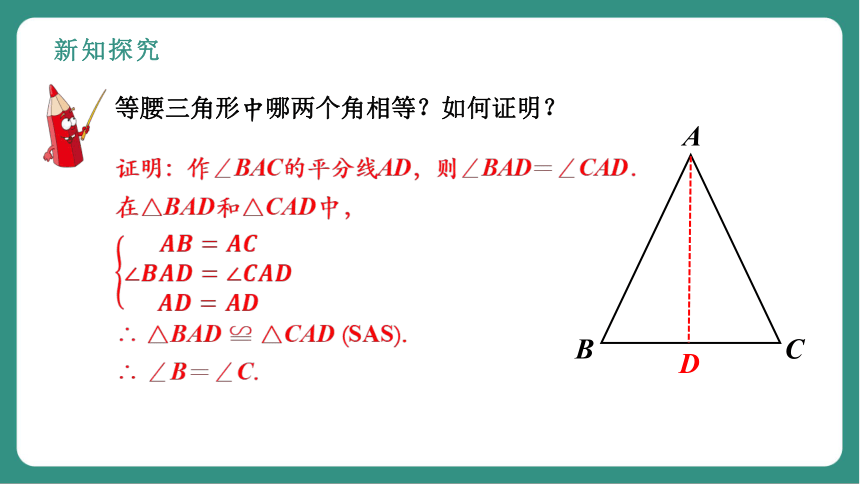
等腰三角形中哪两个角相等?如何证明?
证明:作∠BAC的平分线AD,则∠BAD=∠CAD.
在△BAD和△CAD中,
∴ △BAD ≌ △CAD (SAS).
∴ ∠B=∠C.
新知探究
A
B
C
D
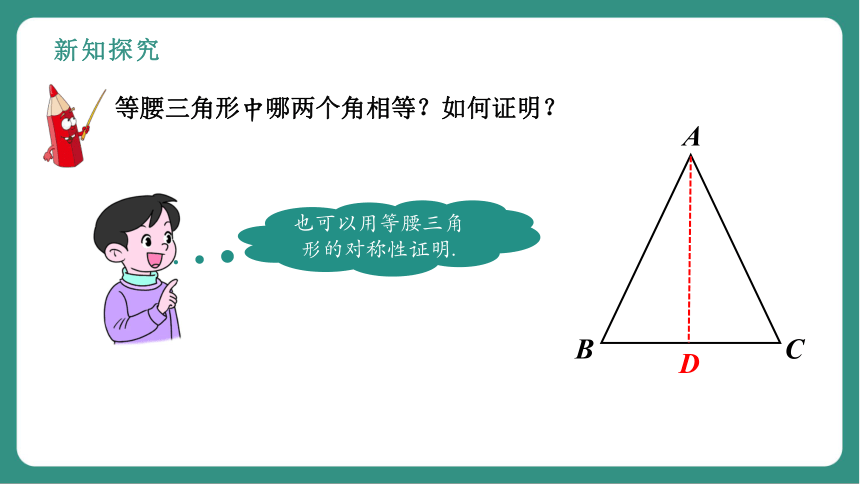
等腰三角形中哪两个角相等?如何证明?
也可以用等腰三角形的对称性证明.
概念引入
等腰三角形中两个相等的角叫作底角.
A
B
C
底角
底角
新知归纳
等腰三角形的两底角相等(简称“等边对等角”).
等腰三角形的性质定理1:
A
B
C
在△ABC中,
∵AB=AC,
∴∠B=∠C (等边对等角).
符号语言:
新知探究
A
B
C
D
由以上证明过程,你还有什么发现?
由以上证明可得,
△ABD≌△ACD,
∴∠BAD=∠CAD,
即AD是△ABC的角平分线.
由△ABD≌△ACD,
∴∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°.
∴AD⊥BC,即AD是△ABC的高.
新知归纳
等腰三角形底边上的高线、中线及顶角平分线重合
(简称“三线合一”).
等腰三角形的性质定理2:
注意:应用“三线合一”的前提条件:
一是等腰三角形;二是三线中要具备一线.
归纳总结
在△ABC中,AB=AC.
(1)∵AD⊥BC,∴AD平分∠BAC,且BD=CD;
(2)∵BD=CD,∴AD平分∠BAC,且AD⊥BC;
(3)∵AD平分∠BAC,∴BD=CD,且AD⊥BC.
A
B
C
D
符号语言:
记忆口诀:一顶三线合.
前提条件
三线中要具备一线
典例分析
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,求证:∠ADB=∠BAC.
A
B
C
D
要证∠ADB=∠BAC
只要找与∠1相等且与∠C也相等的角.
由于∠BAC=∠1+∠2,
∠ADB=∠C+∠2.
只要证∠1=∠C
怎么想
怎么写
?
?
典例分析
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,求证:∠ADB=∠BAC.
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠BAD=∠B(等边对等角)
∴∠C=∠BAD.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠CAD.
∴∠ADB=∠BAD+∠CAD.
∴∠ADB=∠BAC.
A
B
C
D
?
?
典例分析
变式 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
求∠BAC的度数.
解:设∠B=x°.
∵AD=BD,
∴∠BAD=∠B=x°.
∴∠ADC=∠BAD+∠B=(2x)°.
∵DC=AC,
∴∠DAC=∠ADC=(2x)°.
∵AB=AC,
∴∠C=∠B=x°.
∵∠C+∠DAC+∠ADC=180°,
∴x+2x+2x=180.
∴x=36,即∠B=36°.
∴∠BAC=180°-36°-36°=108°.
A
B
C
D
典例分析
例2 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
A
C
B
E
D
图①
G
证明:(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE.
典例分析
例2 已知点D、E在△ABC的边BC上,AB=AC.
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
A
F
C
B
E
D
图②
证明:(2)∵F为DE的中点,
∴DF=EF.
∵BD=CE,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
尝试交流
如图,已知线段a,h,用直尺和圆规作等腰三角形ABC,使底边BC=a,高AD=h.
a
h
作法:
1.作线段BC=a.
2.作线段BC的垂直平分线MN,MN交BC于点D.
3.在MN上截取线段DA,使AD=h.
4.连接AB、AC.
△ABC就是所求作的等腰三角形.
a
M
N
A
●
B
●
●
C
h
●
D
新知巩固
1.在△ABC中,AB=AC.
(1)如果有一个角等于120°,那么∠A=____°,∠B=____°,
∠C=____°;
(2)如果有一个角等于50°,那么另两个角分别等于多少度?
120
30
30
解:如果有一个角等于50°,有以下两种情况:
①当∠A=50°时,∠B=∠C=(180°-∠A)=(180°-50°)=65°.
②当∠B=50°时,∠C=∠B=50°,
∠A=180°-(∠B+∠C) =180°-(50°+50°)=80°.
新知巩固
2.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC,
∴ AD⊥BC.
1
2
解: (1) ∵AB=AC,BD=DC,
∴∠1=∠2=∠BAC.
∵∠BAC=110°,
∴∠1=∠2=55°.
新知巩固
3.如图,AB=AD,CB=CD,连接AC,BD.
求证:AC⊥BD.
C
B
A
D
证明:∵AB=AD,CB=CD,
∴点A、C在BD的垂直平分线上.
∴ AC垂直平分BD,
∴ AC⊥BD.
新知巩固
4.已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:DE=DF.
D
A
B
C
F
E
证明:连接AD.
∵ AB=AC,D是BC的中点,
∴ AD平分∠BAC.
∵ DE⊥AB,DF⊥AC,
∴ DE=DF.
等腰三角形底边中点到两腰的距离相等.
课堂小结
等腰三角形
定义
性质
有两条边相等的三角形叫作等腰三角形.相等的边叫作腰.
等边对等角
三线合一
等腰三角形底边上的高线、中线及顶角平分线重合.
常用辅助线:作顶角平分线、底边上的高、底边上的中线是常见的辅助线.
感谢聆听!
同课章节目录
