【新教材新课标】苏科版数学八年级上册1.4线段垂直平分线与角平分线(第1课时线段垂直平分线的性质)课件(共24张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.4线段垂直平分线与角平分线(第1课时线段垂直平分线的性质)课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 44.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:41:59 | ||
图片预览





文档简介
(共24张PPT)
1.4 线段垂直平分线与角平分线
第1课时 线段垂直平分线的性质
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历探索线段轴对称性的过程,进一步体会轴对称的特性,发展空间观念.
掌握线段垂直平分线的性质定理及其逆定理,并能应用它们进行计算、证明.
通过探索、猜测、证明的过程,进一步发展推理能力.
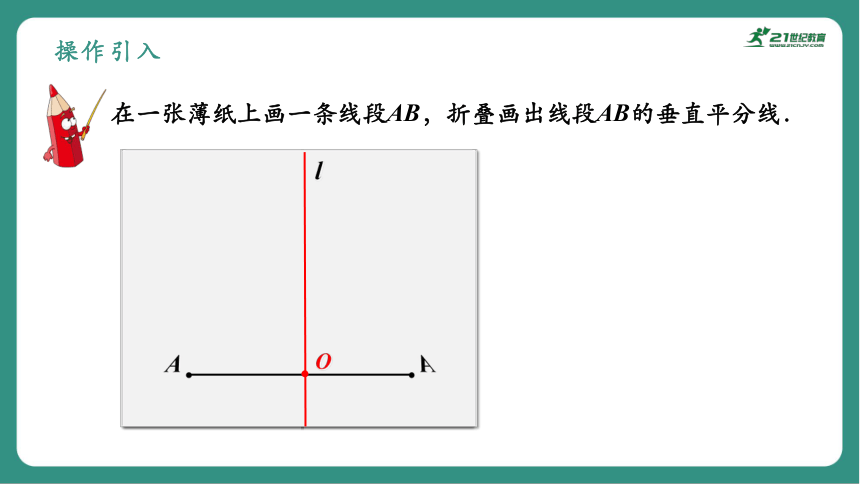
操作引入
在一张薄纸上画一条线段AB,折叠画出线段AB的垂直平分线.
●
●
A
B
●
O
l
●
●
A
B
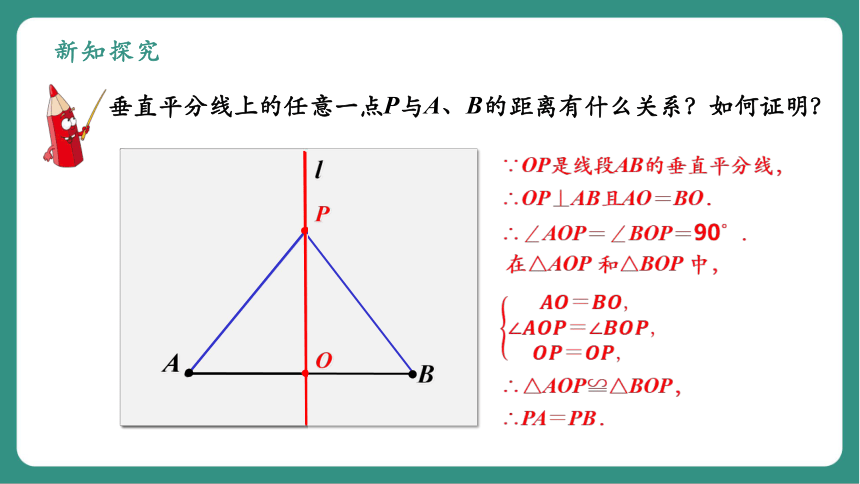
新知探究
垂直平分线上的任意一点P与A、B的距离有什么关系?如何证明?
●
O
l
●
P
∵OP是线段AB的垂直平分线,
∴OP⊥AB且AO=BO.
∴∠AOP=∠BOP=90°.
在△AOP 和△BOP 中,
∴△AOP≌△BOP,
∴PAPB.
新知归纳
线段垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质定理:
任意一点
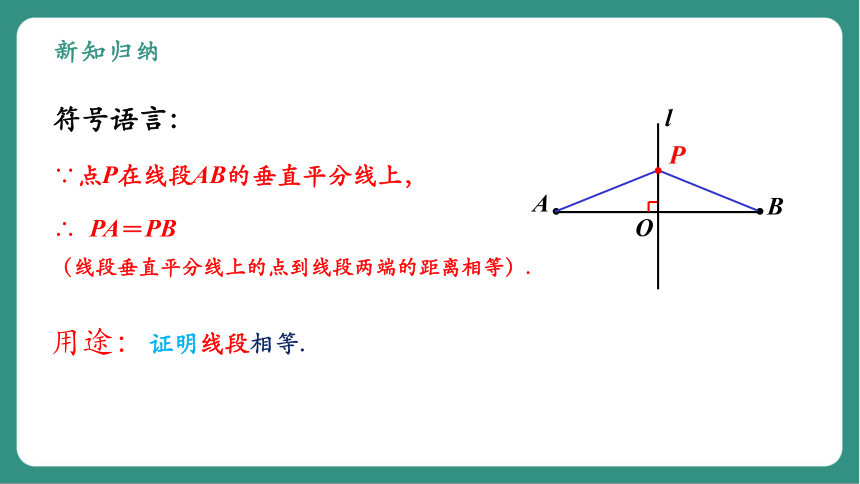
新知归纳
∵点P在线段AB的垂直平分线上,
∴ PA=PB
(线段垂直平分线上的点到线段两端的距离相等).
符号语言:
l
B
A
●
O
●
用途:
证明线段相等.
P
●
讨论交流
如果一个点到一条线段两端的距离相等,那么这个点一定在这条线段的垂直平分线上吗?如何证明?
A
B
●
Q
如图,当点Q在线段AB上时,如果QA=QB,那么Q是线段AB的中点,所以线段AB的垂直平分线一定经过点Q.
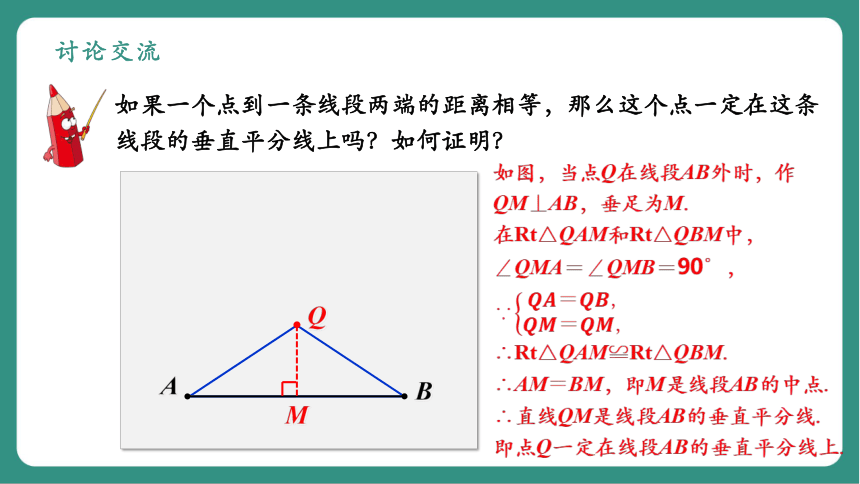
讨论交流
如果一个点到一条线段两端的距离相等,那么这个点一定在这条线段的垂直平分线上吗?如何证明?
A
B
●
Q
M
如图,当点Q在线段AB外时,作
QM⊥AB,垂足为M.
在Rt△QAM和Rt△QBM中,
∠QMA=∠QMB=90°,
∵
∴Rt△QAM≌Rt△QBM.
∴AMBM,即M是线段AB的中点.
∴直线QM是线段AB的垂直平分线.
即点Q一定在线段AB的垂直平分线上.
新知归纳
到线段两端距离相等的点在线段的垂直平分线上.
线段垂直平分线性质定理的逆定理:
线段的垂直平分线是到线段两端距离相等的点的集合.
新知归纳
∵PA=PB,
∴点P在线段AB的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
符号语言:
l
B
A
●
O
●
用途:
确定点在线段的垂直平分线上.
P
●
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
我们把两组邻边分别相等的四边形叫作“筝形”.
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
解:∠BAC=∠DAC,∠ACB=∠ACD,∠ABC=∠ADC,∠ABE=∠ADE,∠CBE=∠CDE,∠AEB=∠AED=∠CEB=∠CED.
在△ABC和△ADC 中,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,∠ACB=∠ACD,∠ABC=∠ADC.
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
在△ABE和△ADE 中,
∴△ABE≌△ADE.
∴∠ABE=∠ADE,∠AEB=∠AED.
同理:△ABE≌△ADE,
∴∠CBE=∠CDE,∠CEB=∠CED.
∵∠AEB=∠CED,∠AED=∠CEB,
∴∠AEB=∠AED=∠CEB=∠CED.
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
你还能得到哪些结论?
AC⊥BD,BE=EB
S四边形ABCD= BD.
直线AC是线段BD的垂直平分线
证明:连接OA、OB、OC.
∵ 点O在AB的垂直平分线l1上,
∴ OA=OB(线段垂直平分线的性质定理)
同理 OA=OC.
∴ OB=OC.
∴ 点O在BC的垂直平分线上
(线段垂直平分线性质定理的逆定理) .
典例分析
例1 如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O.
求证:点O在BC的垂直平分线上
B
A
C
O
l1
l2
归纳总结
三角形三条边的垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
已知线段的垂直平分线时,常考虑将线段垂直平分线上的点到线段两端的距离作出来.
典例分析
变式 利用网格在图中找一点O,使OA=OB=OC.
B
A
C
O
解:点O即为所求 .
新知巩固
1.如图,河边有两个村庄A,B.要在河岸CD上建一个自来水厂P,使水厂到A,B两村的距离相等,请确定点P的位置.
B
C
E
D
F
解:∵点P到A,B两村的距离相等,
∴点P在线段AB的垂直平分线上,即
线段AB的垂直平分线与CD的交点.
如图所示,点P即为所求.
P
A
新知巩固
2.如图,DE是△ABC的边AC的垂直平分线.已知BC=8,AB=10,求△EBC的周长.
B
A
C
D
E
解:∵DE是△ABC的边AC的垂直平分线,
∴AE=CE.
∴BE+CE=BE+AE=AB=10.
∵BC=8,
∴△EBC的周长=BE+CE+BC=10+8=18.
新知巩固
3.如图,AB=AE,BC=ED,AF垂直平分CD,垂足为F.
求证:∠B=∠E.
A
B
C
D
E
F
证明:连接AC,AD.
∵AF垂直平分CD,
∴AC=AD.
在△ABC和△AED 中,
∴△ABC≌△AED,
∴∠B=∠E.
思维提升
如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12 cm. (1)求BC的长;
解:(1)∵l1垂直平分AB,
∴DB=DA,
同理可得EA=EC.
∴BC=BD+DE+EC
=DA+DE+EA
=12 cm.
B
A
E
D
C
l1
O
l2
思维提升
(2)分别连接OA,OB,OC,若△OBC的周长为26 cm,求OA的长.
解:(2)∵l1垂直平分AB,
∴OB=OA.
同理可得OA=OC,
∴OA=OB=OC.
又∵△OBC的周长为26 cm,
BC=12 cm,
∴OB+OC=26-12=14(cm),
∴OB=OC=7 cm,
∴OA=7 cm.
B
A
E
D
C
l1
O
l2
课堂小结
线段垂直平分线的性质
性质定理
见垂直平分线,得线段相等
性质定理的逆定理
判断一个点是否在线段的垂直平分线上.
感谢聆听!
1.4 线段垂直平分线与角平分线
第1课时 线段垂直平分线的性质
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历探索线段轴对称性的过程,进一步体会轴对称的特性,发展空间观念.
掌握线段垂直平分线的性质定理及其逆定理,并能应用它们进行计算、证明.
通过探索、猜测、证明的过程,进一步发展推理能力.
操作引入
在一张薄纸上画一条线段AB,折叠画出线段AB的垂直平分线.
●
●
A
B
●
O
l
●
●
A
B
新知探究
垂直平分线上的任意一点P与A、B的距离有什么关系?如何证明?
●
O
l
●
P
∵OP是线段AB的垂直平分线,
∴OP⊥AB且AO=BO.
∴∠AOP=∠BOP=90°.
在△AOP 和△BOP 中,
∴△AOP≌△BOP,
∴PAPB.
新知归纳
线段垂直平分线上的点到线段两端的距离相等.
线段垂直平分线的性质定理:
任意一点
新知归纳
∵点P在线段AB的垂直平分线上,
∴ PA=PB
(线段垂直平分线上的点到线段两端的距离相等).
符号语言:
l
B
A
●
O
●
用途:
证明线段相等.
P
●
讨论交流
如果一个点到一条线段两端的距离相等,那么这个点一定在这条线段的垂直平分线上吗?如何证明?
A
B
●
Q
如图,当点Q在线段AB上时,如果QA=QB,那么Q是线段AB的中点,所以线段AB的垂直平分线一定经过点Q.
讨论交流
如果一个点到一条线段两端的距离相等,那么这个点一定在这条线段的垂直平分线上吗?如何证明?
A
B
●
Q
M
如图,当点Q在线段AB外时,作
QM⊥AB,垂足为M.
在Rt△QAM和Rt△QBM中,
∠QMA=∠QMB=90°,
∵
∴Rt△QAM≌Rt△QBM.
∴AMBM,即M是线段AB的中点.
∴直线QM是线段AB的垂直平分线.
即点Q一定在线段AB的垂直平分线上.
新知归纳
到线段两端距离相等的点在线段的垂直平分线上.
线段垂直平分线性质定理的逆定理:
线段的垂直平分线是到线段两端距离相等的点的集合.
新知归纳
∵PA=PB,
∴点P在线段AB的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
符号语言:
l
B
A
●
O
●
用途:
确定点在线段的垂直平分线上.
P
●
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
我们把两组邻边分别相等的四边形叫作“筝形”.
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
解:∠BAC=∠DAC,∠ACB=∠ACD,∠ABC=∠ADC,∠ABE=∠ADE,∠CBE=∠CDE,∠AEB=∠AED=∠CEB=∠CED.
在△ABC和△ADC 中,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,∠ACB=∠ACD,∠ABC=∠ADC.
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
在△ABE和△ADE 中,
∴△ABE≌△ADE.
∴∠ABE=∠ADE,∠AEB=∠AED.
同理:△ABE≌△ADE,
∴∠CBE=∠CDE,∠CEB=∠CED.
∵∠AEB=∠CED,∠AED=∠CEB,
∴∠AEB=∠AED=∠CEB=∠CED.
讨论交流
如图,AB=AD,CB=CD,AC、BD相交于点E. 你能在图中找到哪些相等的角?如何证明?
A
D
C
B
E
你还能得到哪些结论?
AC⊥BD,BE=EB
S四边形ABCD= BD.
直线AC是线段BD的垂直平分线
证明:连接OA、OB、OC.
∵ 点O在AB的垂直平分线l1上,
∴ OA=OB(线段垂直平分线的性质定理)
同理 OA=OC.
∴ OB=OC.
∴ 点O在BC的垂直平分线上
(线段垂直平分线性质定理的逆定理) .
典例分析
例1 如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O.
求证:点O在BC的垂直平分线上
B
A
C
O
l1
l2
归纳总结
三角形三条边的垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
已知线段的垂直平分线时,常考虑将线段垂直平分线上的点到线段两端的距离作出来.
典例分析
变式 利用网格在图中找一点O,使OA=OB=OC.
B
A
C
O
解:点O即为所求 .
新知巩固
1.如图,河边有两个村庄A,B.要在河岸CD上建一个自来水厂P,使水厂到A,B两村的距离相等,请确定点P的位置.
B
C
E
D
F
解:∵点P到A,B两村的距离相等,
∴点P在线段AB的垂直平分线上,即
线段AB的垂直平分线与CD的交点.
如图所示,点P即为所求.
P
A
新知巩固
2.如图,DE是△ABC的边AC的垂直平分线.已知BC=8,AB=10,求△EBC的周长.
B
A
C
D
E
解:∵DE是△ABC的边AC的垂直平分线,
∴AE=CE.
∴BE+CE=BE+AE=AB=10.
∵BC=8,
∴△EBC的周长=BE+CE+BC=10+8=18.
新知巩固
3.如图,AB=AE,BC=ED,AF垂直平分CD,垂足为F.
求证:∠B=∠E.
A
B
C
D
E
F
证明:连接AC,AD.
∵AF垂直平分CD,
∴AC=AD.
在△ABC和△AED 中,
∴△ABC≌△AED,
∴∠B=∠E.
思维提升
如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12 cm. (1)求BC的长;
解:(1)∵l1垂直平分AB,
∴DB=DA,
同理可得EA=EC.
∴BC=BD+DE+EC
=DA+DE+EA
=12 cm.
B
A
E
D
C
l1
O
l2
思维提升
(2)分别连接OA,OB,OC,若△OBC的周长为26 cm,求OA的长.
解:(2)∵l1垂直平分AB,
∴OB=OA.
同理可得OA=OC,
∴OA=OB=OC.
又∵△OBC的周长为26 cm,
BC=12 cm,
∴OB+OC=26-12=14(cm),
∴OB=OC=7 cm,
∴OA=7 cm.
B
A
E
D
C
l1
O
l2
课堂小结
线段垂直平分线的性质
性质定理
见垂直平分线,得线段相等
性质定理的逆定理
判断一个点是否在线段的垂直平分线上.
感谢聆听!
同课章节目录
