【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第6课时直角三角形全等的判定)课件(共22张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第6课时直角三角形全等的判定)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 55.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:41:32 | ||
图片预览





文档简介
(共22张PPT)
1.3 全等三角形的判定
第6课时 直角三角形全等的判定
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
探索并掌握直角三角形全等的“斜边、直角边”条件,并能利用这个条件判定两个直角三角形全等,发展推理能力.
会利用基本作图作三角形:已知一直角边和斜边作直角三角形. 理解尺规作图的基本原理和方法,发展空间观念.
问题引入
墙角的三角形置物架坏了,工人师傅量了斜边和一条直角边的长度就做了一个新的,你知道为什么吗?
讨论交流
判断两个直角三角形全等需几个条件?为什么?
因为直角相等,所以还需要两个条件.
讨论交流
判断两个直角三角形全等需几个条件?为什么?
两个锐角相等可以吗?
一边一角呢?两条边呢?
讨论交流
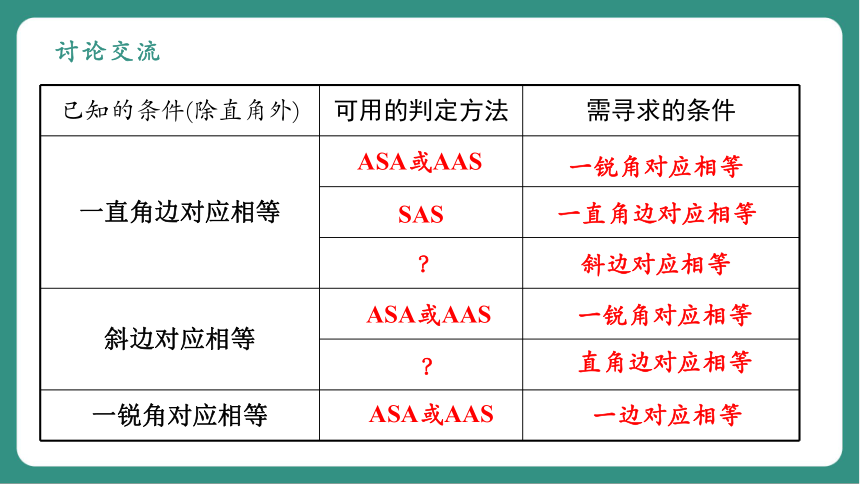
已知的条件(除直角外) 可用的判定方法 需寻求的条件
一直角边对应相等
斜边对应相等
一锐角对应相等
一锐角对应相等
ASA或AAS
一直角边对应相等
SAS
斜边对应相等
?
一锐角对应相等
ASA或AAS
直角边对应相等
?
一边对应相等
ASA或AAS
新知探究
如图,给定直角三角形ABC (Rt△ABC),按下列作法,在透明纸上用直尺和圆规作△A'B'C′.
B
C
A
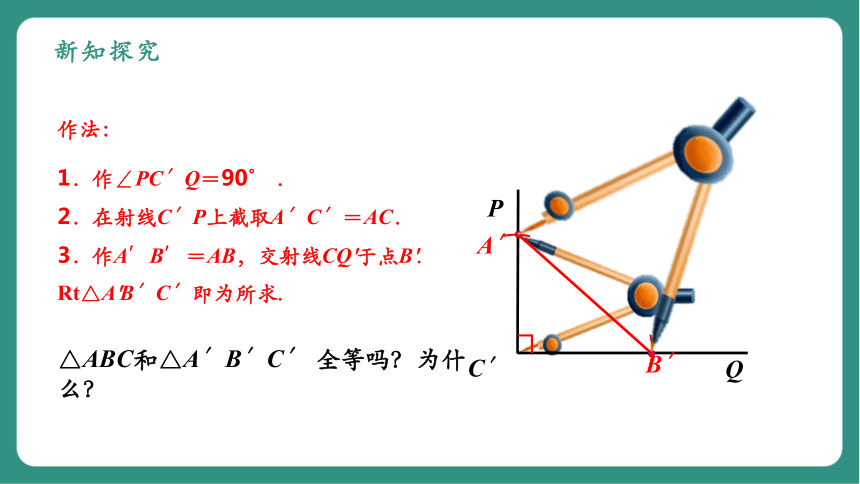
新知探究
作法:
1.作∠PC′Q=90° .
2.在射线C′P上截取A′C′=AC.
3.作A′B′=AB,交射线CQ'于点B'.
Rt△A'B′C′即为所求.
Q
C′
P
A′
B′
△ABC和△A′B′C′ 全等吗?为什么?
B
C
A
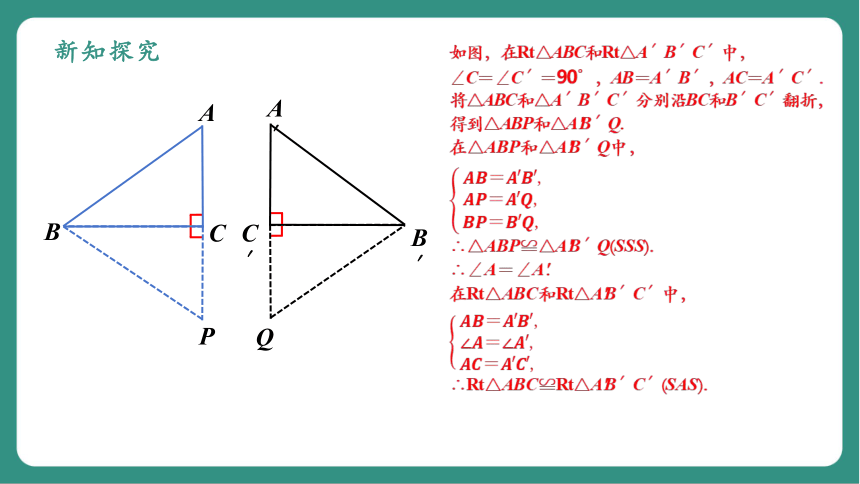
新知探究
C′
B′
A′
P
Q
如图,在Rt△ABC和Rt△A′B′C′中,
∠C=∠C′=90°,AB=A′B′,AC=A′C′.
将△ABC和△A′B′C′分别沿BC和B′C′翻折,
得到△ABP和△A'B′Q.
在△ABP和△A'B′Q中,
∴△ABP≌△A'B′Q(SSS).
∴∠A=∠A'.
在Rt△ABC和Rt△A'B′C′中,
∴Rt△ABC≌Rt△A'B′C′(SAS).
新知探究
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“HL”).
于是,我们得到如下定理:
前提
这个定理可以用来判定两个直角三角形全等.
新知探究
符号语言:
在Rt△ABC和Rt△A′B′C′中,
∠C=∠C′=90°,如果
那么 Rt△ABC≌Rt△ A′B′C′ (HL).
A
B
C
A ′
B′
C ′
不要丢了
\
\
\\
\\
典例分析
例1 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
A
D
C
B
O
分析:
1. AO与BO,CO与DO分别属于哪两个三角形?
2.证△ACO≌△BDO已有哪些条件?还缺什么条件?
3. AC、BD还属于哪两个三角形?
典例分析
证明:在△ABC 和△BAD 中,∠C=∠D=90°,
∴ Rt△ABC≌Rt△BAD (HL).
∴ AC=BD.
在△AOC 和△BOD 中,
∴△AOC≌△BOD,
∴AOBO,CODO.
A
D
C
B
O
例1 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
注意“HL”的前提条件是在直角三角形中.
典例分析
变式 已知:如图,AD、BC相交于点O,AC=BD,∠C=∠D=90°,求证:AD=BC.
证明:在△AOC 和△BOD 中,
∴△AOC≌△BOD(AAS)
∴AOBO,CODO.
∴AO+DOBO+CO (等式性质).
即ADBC
也可以证Rt△ABD≌Rt△BAC(HL)
A
D
C
B
O
典例分析
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
E
D
A
C
B
F
证明:∵ AD,AF分别是△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
在Rt△ADC和Rt△AFE中,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
在Rt△ADB和Rt△AFB中,
∴Rt△ADB≌Rt△AFB(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
新知巩固
A
D
B
C
1. 如图,方格纸中有格点A,B,C,D,以其中的三个点为顶点,画出所有的直角三角形,并找出其中全等的直角三角形.
Rt△ADC
Rt△ABD
Rt△CBD
Rt△ABD≌Rt△CBD
新知巩固
2. 如图,AC⊥CB,AD⊥DB,要证明△ACB≌△ADB,还需要什么条件?
D
A
B
C
解:∵AC⊥CB,AD⊥DB,
∴∠C=∠D=90°,
又∵AB=AB,
当添加条件AD=AC或BD=BC,
可用 HL证明△ABC≌△ABD;
当添加条件∠DAB=∠CAB或∠DBA=∠CBA,
可用AAS证明△ABC≌△ABD.
新知巩固
3. 如图,AD=BC,CA⊥AB,AC⊥CD. 求证:AD∥BC.
D
A
B
C
证明:∵ CA⊥AB,AC⊥CD,
∴∠BAC=∠DCA=90°.
在Rt△BAC和Rt△DCA中
∴Rt△BAC≌Rt△DCA(HL).
∴∠ACB=∠DAC,
∴ AD∥BC.
新知巩固
4. 如图,在△ABC中,AB=AC,AD是高,DE⊥AB,DF⊥AC,垂足分别为E,F. 求证:DE=DF.
D
A
B
C
E
F
证明:∵AD是高,
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中
∴Rt△ADB≌Rt△ADC(HL).
∴∠BAD=∠CAD.
新知巩固
4. 如图,在△ABC中,AB=AC,AD是高,DE⊥AB,DF⊥AC,垂足分别为E,F. 求证:DE=DF.
D
A
B
C
E
F
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在Rt△ADE和Rt△ADF中
∴Rt△ADE≌Rt△ADF(AAS).
∴DE=DF.
课堂小结
HL判定
条件
斜边+一条直角边(隐含条件:直角相等)
作图验证
应用
感谢聆听!
1.3 全等三角形的判定
第6课时 直角三角形全等的判定
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
探索并掌握直角三角形全等的“斜边、直角边”条件,并能利用这个条件判定两个直角三角形全等,发展推理能力.
会利用基本作图作三角形:已知一直角边和斜边作直角三角形. 理解尺规作图的基本原理和方法,发展空间观念.
问题引入
墙角的三角形置物架坏了,工人师傅量了斜边和一条直角边的长度就做了一个新的,你知道为什么吗?
讨论交流
判断两个直角三角形全等需几个条件?为什么?
因为直角相等,所以还需要两个条件.
讨论交流
判断两个直角三角形全等需几个条件?为什么?
两个锐角相等可以吗?
一边一角呢?两条边呢?
讨论交流
已知的条件(除直角外) 可用的判定方法 需寻求的条件
一直角边对应相等
斜边对应相等
一锐角对应相等
一锐角对应相等
ASA或AAS
一直角边对应相等
SAS
斜边对应相等
?
一锐角对应相等
ASA或AAS
直角边对应相等
?
一边对应相等
ASA或AAS
新知探究
如图,给定直角三角形ABC (Rt△ABC),按下列作法,在透明纸上用直尺和圆规作△A'B'C′.
B
C
A
新知探究
作法:
1.作∠PC′Q=90° .
2.在射线C′P上截取A′C′=AC.
3.作A′B′=AB,交射线CQ'于点B'.
Rt△A'B′C′即为所求.
Q
C′
P
A′
B′
△ABC和△A′B′C′ 全等吗?为什么?
B
C
A
新知探究
C′
B′
A′
P
Q
如图,在Rt△ABC和Rt△A′B′C′中,
∠C=∠C′=90°,AB=A′B′,AC=A′C′.
将△ABC和△A′B′C′分别沿BC和B′C′翻折,
得到△ABP和△A'B′Q.
在△ABP和△A'B′Q中,
∴△ABP≌△A'B′Q(SSS).
∴∠A=∠A'.
在Rt△ABC和Rt△A'B′C′中,
∴Rt△ABC≌Rt△A'B′C′(SAS).
新知探究
斜边和一条直角边分别相等的两个直角三角形全等
(简写成“HL”).
于是,我们得到如下定理:
前提
这个定理可以用来判定两个直角三角形全等.
新知探究
符号语言:
在Rt△ABC和Rt△A′B′C′中,
∠C=∠C′=90°,如果
那么 Rt△ABC≌Rt△ A′B′C′ (HL).
A
B
C
A ′
B′
C ′
不要丢了
\
\
\\
\\
典例分析
例1 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
A
D
C
B
O
分析:
1. AO与BO,CO与DO分别属于哪两个三角形?
2.证△ACO≌△BDO已有哪些条件?还缺什么条件?
3. AC、BD还属于哪两个三角形?
典例分析
证明:在△ABC 和△BAD 中,∠C=∠D=90°,
∴ Rt△ABC≌Rt△BAD (HL).
∴ AC=BD.
在△AOC 和△BOD 中,
∴△AOC≌△BOD,
∴AOBO,CODO.
A
D
C
B
O
例1 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
注意“HL”的前提条件是在直角三角形中.
典例分析
变式 已知:如图,AD、BC相交于点O,AC=BD,∠C=∠D=90°,求证:AD=BC.
证明:在△AOC 和△BOD 中,
∴△AOC≌△BOD(AAS)
∴AOBO,CODO.
∴AO+DOBO+CO (等式性质).
即ADBC
也可以证Rt△ABD≌Rt△BAC(HL)
A
D
C
B
O
典例分析
例2 如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
E
D
A
C
B
F
证明:∵ AD,AF分别是△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
在Rt△ADC和Rt△AFE中,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
在Rt△ADB和Rt△AFB中,
∴Rt△ADB≌Rt△AFB(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
新知巩固
A
D
B
C
1. 如图,方格纸中有格点A,B,C,D,以其中的三个点为顶点,画出所有的直角三角形,并找出其中全等的直角三角形.
Rt△ADC
Rt△ABD
Rt△CBD
Rt△ABD≌Rt△CBD
新知巩固
2. 如图,AC⊥CB,AD⊥DB,要证明△ACB≌△ADB,还需要什么条件?
D
A
B
C
解:∵AC⊥CB,AD⊥DB,
∴∠C=∠D=90°,
又∵AB=AB,
当添加条件AD=AC或BD=BC,
可用 HL证明△ABC≌△ABD;
当添加条件∠DAB=∠CAB或∠DBA=∠CBA,
可用AAS证明△ABC≌△ABD.
新知巩固
3. 如图,AD=BC,CA⊥AB,AC⊥CD. 求证:AD∥BC.
D
A
B
C
证明:∵ CA⊥AB,AC⊥CD,
∴∠BAC=∠DCA=90°.
在Rt△BAC和Rt△DCA中
∴Rt△BAC≌Rt△DCA(HL).
∴∠ACB=∠DAC,
∴ AD∥BC.
新知巩固
4. 如图,在△ABC中,AB=AC,AD是高,DE⊥AB,DF⊥AC,垂足分别为E,F. 求证:DE=DF.
D
A
B
C
E
F
证明:∵AD是高,
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中
∴Rt△ADB≌Rt△ADC(HL).
∴∠BAD=∠CAD.
新知巩固
4. 如图,在△ABC中,AB=AC,AD是高,DE⊥AB,DF⊥AC,垂足分别为E,F. 求证:DE=DF.
D
A
B
C
E
F
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在Rt△ADE和Rt△ADF中
∴Rt△ADE≌Rt△ADF(AAS).
∴DE=DF.
课堂小结
HL判定
条件
斜边+一条直角边(隐含条件:直角相等)
作图验证
应用
感谢聆听!
同课章节目录
