【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第5课时)课件(共18张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第5课时)课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 41.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:52:29 | ||
图片预览



文档简介
(共18张PPT)
1.3 全等三角形的判定
第5课时
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
进一步掌握SSS、SAS、ASA、AAS四种三角形全等的判定方法及其适用条件.
能在具体图形中识别出满足全等条件的两个三角形,并能按照清晰的步骤书写证明过程.
能利用全等三角形的性质进行简单的推理,解决像“证明边相等”、“证明角相等”这类问题.
问题引入
三角形全等满足的条件是什么?
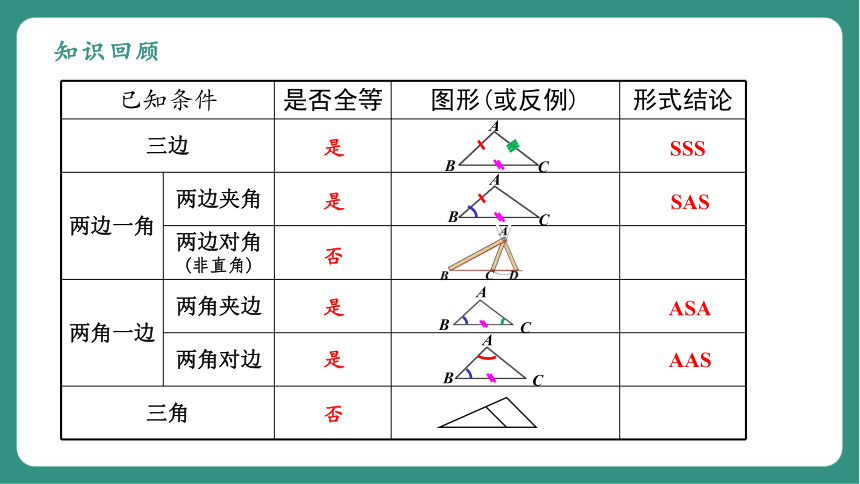
已知条件 是否全等 图形(或反例) 形式结论
三边
两边一角 两边夹角
两边对角 (非直角)
两角一边 两角夹边
两角对边
三角
知识回顾
SSS
SAS
ASA
AAS
是
是
否
是
是
否
A
B
C
A
B
C
A
B
C
A
B
C
典例分析
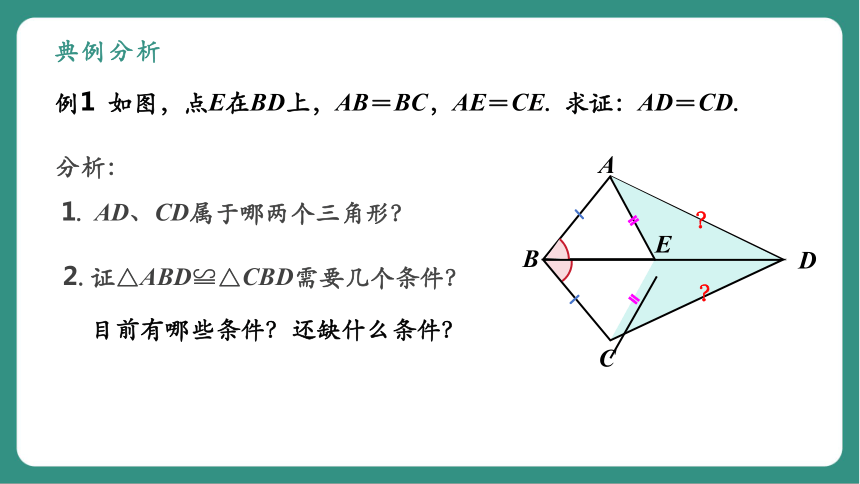
例1 如图,点E在BD上,AB=BC,AE=CE. 求证:AD=CD.
A
B
C
D
E
?
?
分析:
1. AD、CD属于哪两个三角形?
2. 证△ABD≌△CBD需要几个条件?
目前有哪些条件?还缺什么条件?
典例分析
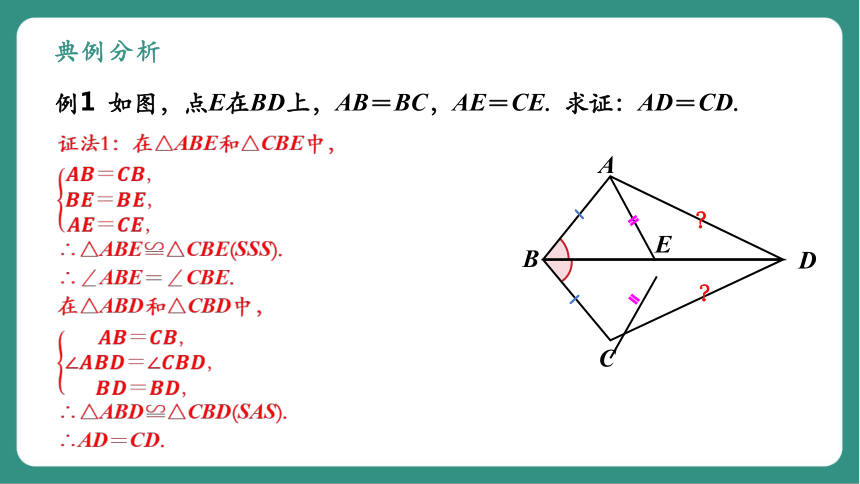
例1 如图,点E在BD上,AB=BC,AE=CE. 求证:AD=CD.
A
B
C
D
E
?
?
证法1:在△ABE和△CBE中,
∴△ABE≌△CBE(SSS).
∴∠ABE=∠CBE.
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS).
∴AD=CD.
典例分析
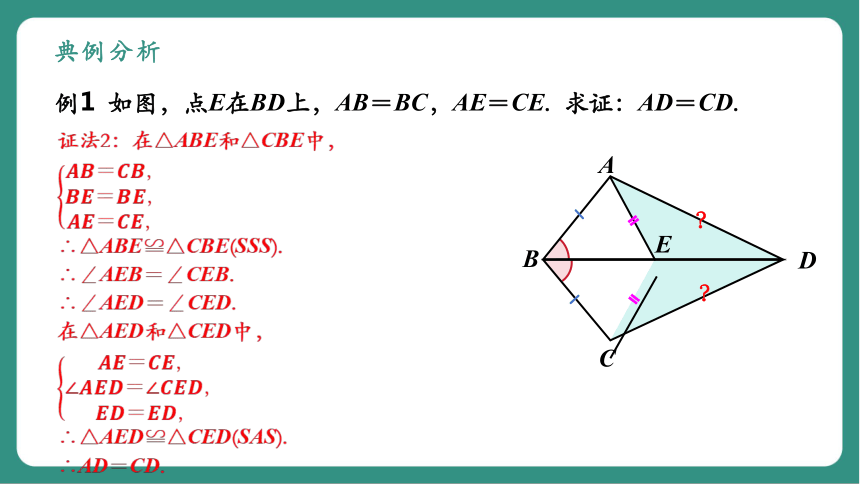
例1 如图,点E在BD上,AB=BC,AE=CE. 求证:AD=CD.
A
B
C
D
E
?
?
证法2:在△ABE和△CBE中,
∴△ABE≌△CBE(SSS).
∴∠AEB=∠CEB.
∴∠AED=∠CED.
在△AED和△CED中,
∴△AED≌△CED(SAS).
∴AD=CD.
典例分析
例2 如图,AB⊥BD,ED⊥BD,垂足分别为B,D,点C在BD上,AB=CD,BC=DE. 求证:AC与CE垂直且相等.
A
B
C
D
E
分析:
1. AC、CE属于哪两个三角形?
2. 在△ABC和△CDE中,有哪些条件?
3. 要证AC⊥CE,只要证哪个角是90°?
如何得到这个角是90°?
典例分析
例2 如图,AB⊥BD,ED⊥BD,垂足分别为B,D,点C在BD上,AB=CD,BC=DE. 求证:AC与CE垂直且相等.
A
B
C
D
E
证明:∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°.
在△ABC和△CDE中,
∴△ABC≌△CDE (SAS).
∴∠A=∠ECD,AC=CE.
∵∠B=90°,
∴∠A+∠ACB=90°.
∴∠ECD+∠ACB=90°.
∴∠ACE=90°.
∴AC与CE垂直且相等.
新知巩固
1.如图,∠ABD=90°,AB=BD,AC⊥BC,DE⊥BC,垂足分别为C、E. (1)求证:△ABC≌△BDE;
解:(1)证明:∵AC⊥BC,DE⊥BC,
∴∠C=∠DEB=90°.
∴∠D+∠DBE=90°.
∵∠ABD=90°,
∴∠DBE+∠ABC=90°,
∴∠D=∠ABC.
在△ABC和△BDE中,
∴△ABC≌△BDE (AAS).
0
C
D
A
B
E
新知巩固
(2) 判断线段DE,CE,AC之间的数量关系,并证明你的结论.
解:(2) DE=AC+CE.
证明如下:∵△ABC≌△BDE,
∴ AC=BE,BC=DE.
∵BC=BE+CE,
∴ DE=AC+CE.
0
C
D
A
B
E
新知巩固
2. 如图,在△ABC中,AB=AC,高BD,CE交于点O.
求证:(1) BO=OC.
A
B
C
E
D
O
证明:(1)∵BD,CE是高线,
∴∠ADB=∠AEC=∠BEO=∠CDO=90°.
在△ABD和△ACE中,
∴△ABD≌△ACE (AAS).
∴AD=AE,
新知巩固
2. 如图,在△ABC中,AB=AC,高BD,CE交于点O.
求证:(1) BO=OC.
A
B
C
E
D
O
∴ AB-AE=AC-AD,
即BE=CD.
在△BEO和△CDO中,
∴△BEO≌△CDO (AAS).
∴OB=OC.
新知巩固
2. 如图,在△ABC中,AB=AC,高BD,CE交于点O.
(2) 若∠ABC=50°,求∠BOC的度数.
A
B
C
E
D
O
解:(2)∵∠ABC=50°,∠BEC=90°,
∴∠ECB=40°.
∵△ABD≌△ACE,
∴BD=CE.
在△BCD和△CBE中,
∴△BCD≌△CBE (SAS).
∴∠DBC=∠ECB=40°.
∴∠BOC=180°-∠ECB-∠DBC=180°-40°-40°=100°.
新知巩固
3.如图,AD,BF相交于点O,AB=DF. 点E,C在BF上,BE=FC,AC=DE. 求证:AO=DO,BO=FO.
A
B
C
E
D
F
O
证明: ∵BE=FC,
∴ BE+CE=FC+CE,
即 BC=FE.
在△ABC和△DFE中,
∴△ABC≌△DFE (SSS).
∴∠ABO=∠DFO.
新知巩固
3.如图,AD,BF相交于点O,AB=DF. 点E,C在BF上,BE=FC,AC=DE. 求证:AO=DO,BO=FO.
A
B
C
E
D
F
O
在△ABO和△DFO中,
∴△ABO≌△DFO (AAS).
∴AO=DO,BO=FO.
课堂小结
(1)直接条件:即已知中直接给出的三角形的对应边或对应角.
证明三角形全等的“三类条件”:
(2)隐含条件:即已知没有给出,但通过读图得到的条件.
如:公共边、公共角、对顶角、直角相等.
(3)间接条件:即已知中所给条件不是三角形的对应边和对应角,需要进一步推理.
①等边、等角加(减)等边、等角,其和(差)相等;
②同角或等角的余(补)角相等;
③根据角平分线、平行线得角相等,由中线的定义得边相等.
感谢聆听!
1.3 全等三角形的判定
第5课时
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
进一步掌握SSS、SAS、ASA、AAS四种三角形全等的判定方法及其适用条件.
能在具体图形中识别出满足全等条件的两个三角形,并能按照清晰的步骤书写证明过程.
能利用全等三角形的性质进行简单的推理,解决像“证明边相等”、“证明角相等”这类问题.
问题引入
三角形全等满足的条件是什么?
已知条件 是否全等 图形(或反例) 形式结论
三边
两边一角 两边夹角
两边对角 (非直角)
两角一边 两角夹边
两角对边
三角
知识回顾
SSS
SAS
ASA
AAS
是
是
否
是
是
否
A
B
C
A
B
C
A
B
C
A
B
C
典例分析
例1 如图,点E在BD上,AB=BC,AE=CE. 求证:AD=CD.
A
B
C
D
E
?
?
分析:
1. AD、CD属于哪两个三角形?
2. 证△ABD≌△CBD需要几个条件?
目前有哪些条件?还缺什么条件?
典例分析
例1 如图,点E在BD上,AB=BC,AE=CE. 求证:AD=CD.
A
B
C
D
E
?
?
证法1:在△ABE和△CBE中,
∴△ABE≌△CBE(SSS).
∴∠ABE=∠CBE.
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS).
∴AD=CD.
典例分析
例1 如图,点E在BD上,AB=BC,AE=CE. 求证:AD=CD.
A
B
C
D
E
?
?
证法2:在△ABE和△CBE中,
∴△ABE≌△CBE(SSS).
∴∠AEB=∠CEB.
∴∠AED=∠CED.
在△AED和△CED中,
∴△AED≌△CED(SAS).
∴AD=CD.
典例分析
例2 如图,AB⊥BD,ED⊥BD,垂足分别为B,D,点C在BD上,AB=CD,BC=DE. 求证:AC与CE垂直且相等.
A
B
C
D
E
分析:
1. AC、CE属于哪两个三角形?
2. 在△ABC和△CDE中,有哪些条件?
3. 要证AC⊥CE,只要证哪个角是90°?
如何得到这个角是90°?
典例分析
例2 如图,AB⊥BD,ED⊥BD,垂足分别为B,D,点C在BD上,AB=CD,BC=DE. 求证:AC与CE垂直且相等.
A
B
C
D
E
证明:∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°.
在△ABC和△CDE中,
∴△ABC≌△CDE (SAS).
∴∠A=∠ECD,AC=CE.
∵∠B=90°,
∴∠A+∠ACB=90°.
∴∠ECD+∠ACB=90°.
∴∠ACE=90°.
∴AC与CE垂直且相等.
新知巩固
1.如图,∠ABD=90°,AB=BD,AC⊥BC,DE⊥BC,垂足分别为C、E. (1)求证:△ABC≌△BDE;
解:(1)证明:∵AC⊥BC,DE⊥BC,
∴∠C=∠DEB=90°.
∴∠D+∠DBE=90°.
∵∠ABD=90°,
∴∠DBE+∠ABC=90°,
∴∠D=∠ABC.
在△ABC和△BDE中,
∴△ABC≌△BDE (AAS).
0
C
D
A
B
E
新知巩固
(2) 判断线段DE,CE,AC之间的数量关系,并证明你的结论.
解:(2) DE=AC+CE.
证明如下:∵△ABC≌△BDE,
∴ AC=BE,BC=DE.
∵BC=BE+CE,
∴ DE=AC+CE.
0
C
D
A
B
E
新知巩固
2. 如图,在△ABC中,AB=AC,高BD,CE交于点O.
求证:(1) BO=OC.
A
B
C
E
D
O
证明:(1)∵BD,CE是高线,
∴∠ADB=∠AEC=∠BEO=∠CDO=90°.
在△ABD和△ACE中,
∴△ABD≌△ACE (AAS).
∴AD=AE,
新知巩固
2. 如图,在△ABC中,AB=AC,高BD,CE交于点O.
求证:(1) BO=OC.
A
B
C
E
D
O
∴ AB-AE=AC-AD,
即BE=CD.
在△BEO和△CDO中,
∴△BEO≌△CDO (AAS).
∴OB=OC.
新知巩固
2. 如图,在△ABC中,AB=AC,高BD,CE交于点O.
(2) 若∠ABC=50°,求∠BOC的度数.
A
B
C
E
D
O
解:(2)∵∠ABC=50°,∠BEC=90°,
∴∠ECB=40°.
∵△ABD≌△ACE,
∴BD=CE.
在△BCD和△CBE中,
∴△BCD≌△CBE (SAS).
∴∠DBC=∠ECB=40°.
∴∠BOC=180°-∠ECB-∠DBC=180°-40°-40°=100°.
新知巩固
3.如图,AD,BF相交于点O,AB=DF. 点E,C在BF上,BE=FC,AC=DE. 求证:AO=DO,BO=FO.
A
B
C
E
D
F
O
证明: ∵BE=FC,
∴ BE+CE=FC+CE,
即 BC=FE.
在△ABC和△DFE中,
∴△ABC≌△DFE (SSS).
∴∠ABO=∠DFO.
新知巩固
3.如图,AD,BF相交于点O,AB=DF. 点E,C在BF上,BE=FC,AC=DE. 求证:AO=DO,BO=FO.
A
B
C
E
D
F
O
在△ABO和△DFO中,
∴△ABO≌△DFO (AAS).
∴AO=DO,BO=FO.
课堂小结
(1)直接条件:即已知中直接给出的三角形的对应边或对应角.
证明三角形全等的“三类条件”:
(2)隐含条件:即已知没有给出,但通过读图得到的条件.
如:公共边、公共角、对顶角、直角相等.
(3)间接条件:即已知中所给条件不是三角形的对应边和对应角,需要进一步推理.
①等边、等角加(减)等边、等角,其和(差)相等;
②同角或等角的余(补)角相等;
③根据角平分线、平行线得角相等,由中线的定义得边相等.
感谢聆听!
同课章节目录
