【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第4课时边边边)课件(共21张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第4课时边边边)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 64.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:52:07 | ||
图片预览



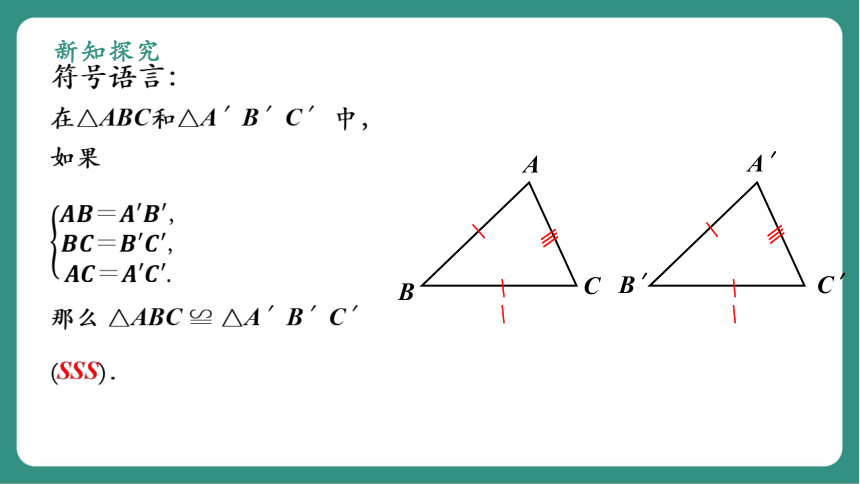
文档简介
(共21张PPT)
1.3 全等三角形的判定
第4课时 边边边
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
探索并掌握三角形全等的“边边边”条件,并能利用这个条件判定两个三角形全等,发展推理能力.
会利用基本作图作三角形:已知三边作三角形,理解尺规作图的基本原理和方法,发展空间观念.
了解三角形的稳定性及其在生活中的应用.
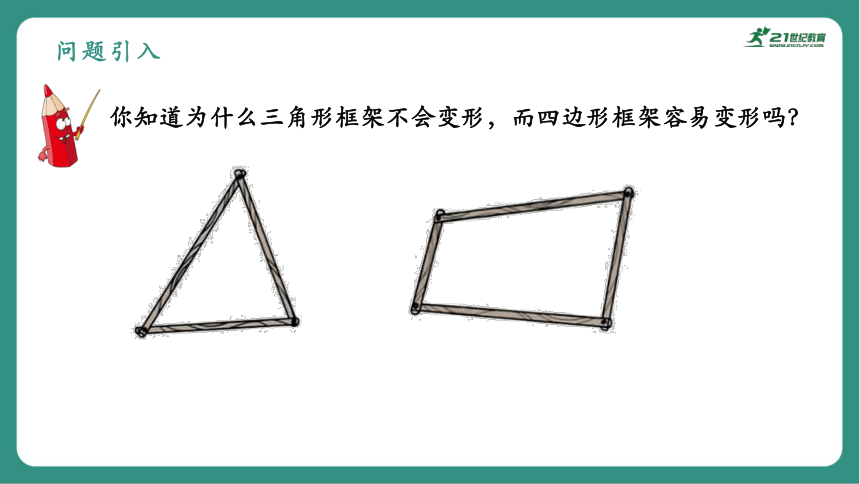
问题引入
你知道为什么三角形框架不会变形,而四边形框架容易变形吗?
知识回顾
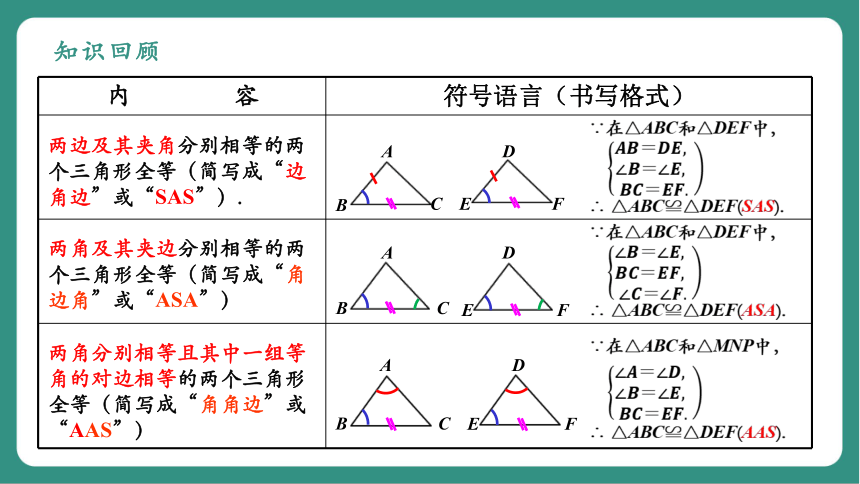
内 容 符号语言(书写格式)
两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”)
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
∵在△ABC和△DEF中,
∴ △ABC≌△DEF(SAS).
∵在△ABC和△DEF中,
∴ △ABC≌△DEF(ASA).
∵在△ABC和△MNP中,
∴ △ABC≌△DEF(AAS).
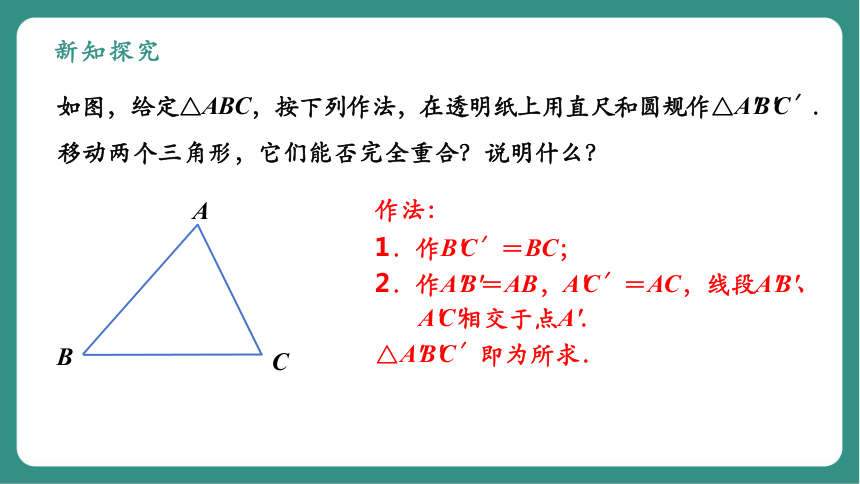
新知探究
如图,给定△ABC,按下列作法,在透明纸上用直尺和圆规作△A'B'C′.
B
C
A
作法:
1.作B'C′=BC;
2.作A'B'=AB,A'C′=AC,线段A'B'、
A'C'相交于点A'.
△A'B'C′即为所求.
移动两个三角形,它们能否完全重合?说明什么?
新知探究
三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
通过实践,人们得到了如下基本事实:
这个基本事实可以用来判定两个三角形全等.
符号语言:
在△ABC和△A′B′C′ 中,如果
那么 △ABC ≌ △A′B′C′ (SSS).
新知探究
A
B
C
A′
B′
C′
\\
\
≡
\\
\
≡
典例分析
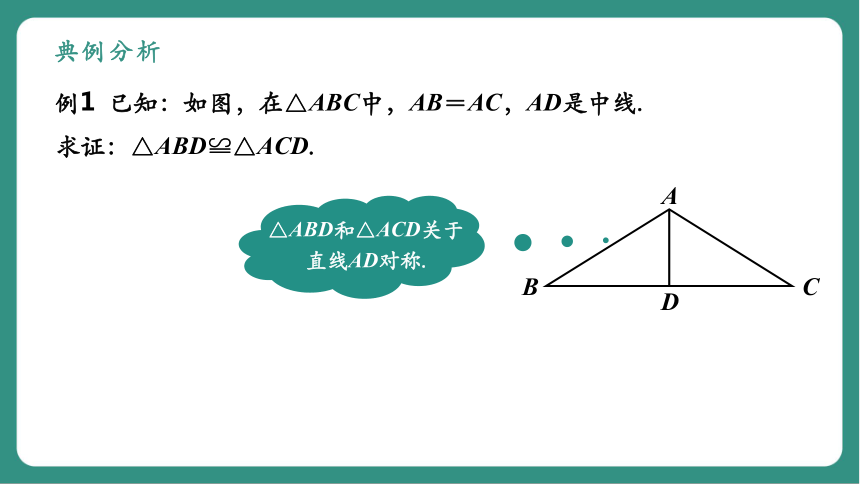
例1 已知:如图,在△ABC中,AB=AC,AD是中线.
求证:△ABD≌△ACD.
A
B
C
D
△ABD和△ACD关于直线AD对称.
典例分析
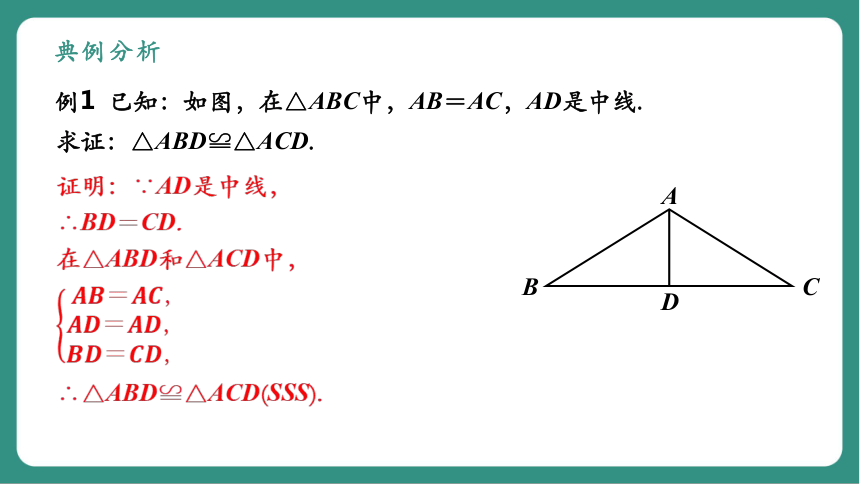
例1 已知:如图,在△ABC中,AB=AC,AD是中线.
求证:△ABD≌△ACD.
A
B
C
D
证明:∵AD是中线,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
典例分析
变式 已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C.
A
B
C
D
证明:作△ABC的中线AD.
∵AD是中线,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
可以作△ABC的角平分线或高吗?
典例分析
例2 已知:如图,AB=DE,AC=DF,BE=CF.
求证:△ABC≌△DEF.
A
B
C
D
E
F
其中一个三角形沿直线BC平移后,能与另一个三角形重合.
典例分析
例2 已知:如图,AB=DE,AC=DF,BE=CF.
求证:△ABC≌△DEF.
A
B
C
D
E
F
证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
∴ △ABC≌△DEF (SSS).
典例分析
变式 已知,AB=DC,DB=AC.
求证:∠ABD=∠DCA.
A
C
B
D
证明:连接AD .
在△ABD和△DCA中,
∴△ABD≌△DCA (SSS),
∴∠ABD=∠DCA.
可以连接B C吗?
新知巩固
1. 如图,四边形ABCD是正方形,连接AC. 求∠BAC的度数.
A
C
B
D
证明:∵四边形ABCD是正方形,
∴AB=BC=DC=AD,∠BAD=90°.
在△ABC和△ADC中,
∴△ABC≌△ADC (SSS),
∴∠BAC=∠DAC.
∵∠BAC+∠DAC=∠BAD=90°,
∴∠BAC=45°.
新知巩固
2. 如图,点C,D在AB上,PA=PB,AC=BD,PC=PD.
求证:△PAD≌△PBC.
证明:∵AC=BD,
∴AC+CD=BD+EC.
即AD=BC.
在△PAD和△PBC中,
∴△PAD≌△PBC.
A
P
C
B
D
新知巩固
3.已知:如图,AB=CD,AD=CB,
求证:(1)∠A=∠C;(2)AB∥DC,AD∥BC.
A
C
D
B
证明:(1)连接BD .
在△ABD和△CDB中,
∴△ABD≌△CDB.
∴∠A=∠C.
(2) ∵ △ABD≌△CDB,
∴∠ABD=∠CDB, ∠ADB=∠CBD .
∴AB∥DC,AD∥BC.
讨论交流
你知道为什么三角形框架不会变形了吗?
如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定. 三角形的这个性质叫做三角形的稳定性.
讨论交流
三角形的稳定性在生活中有广泛的应用.你能举出一些例子吗
空调外机支架
塔式起重机
讨论交流
三角形的稳定性在生活中有广泛的应用.你能举出一些例子吗
课堂小结
SSS判定
条件
三边
作图验证
应用
初步了解添加辅助线构造全等三角形
三角形的稳定性
感谢聆听!
1.3 全等三角形的判定
第4课时 边边边
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
探索并掌握三角形全等的“边边边”条件,并能利用这个条件判定两个三角形全等,发展推理能力.
会利用基本作图作三角形:已知三边作三角形,理解尺规作图的基本原理和方法,发展空间观念.
了解三角形的稳定性及其在生活中的应用.
问题引入
你知道为什么三角形框架不会变形,而四边形框架容易变形吗?
知识回顾
内 容 符号语言(书写格式)
两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”)
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
∵在△ABC和△DEF中,
∴ △ABC≌△DEF(SAS).
∵在△ABC和△DEF中,
∴ △ABC≌△DEF(ASA).
∵在△ABC和△MNP中,
∴ △ABC≌△DEF(AAS).
新知探究
如图,给定△ABC,按下列作法,在透明纸上用直尺和圆规作△A'B'C′.
B
C
A
作法:
1.作B'C′=BC;
2.作A'B'=AB,A'C′=AC,线段A'B'、
A'C'相交于点A'.
△A'B'C′即为所求.
移动两个三角形,它们能否完全重合?说明什么?
新知探究
三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
通过实践,人们得到了如下基本事实:
这个基本事实可以用来判定两个三角形全等.
符号语言:
在△ABC和△A′B′C′ 中,如果
那么 △ABC ≌ △A′B′C′ (SSS).
新知探究
A
B
C
A′
B′
C′
\\
\
≡
\\
\
≡
典例分析
例1 已知:如图,在△ABC中,AB=AC,AD是中线.
求证:△ABD≌△ACD.
A
B
C
D
△ABD和△ACD关于直线AD对称.
典例分析
例1 已知:如图,在△ABC中,AB=AC,AD是中线.
求证:△ABD≌△ACD.
A
B
C
D
证明:∵AD是中线,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
典例分析
变式 已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C.
A
B
C
D
证明:作△ABC的中线AD.
∵AD是中线,
∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
可以作△ABC的角平分线或高吗?
典例分析
例2 已知:如图,AB=DE,AC=DF,BE=CF.
求证:△ABC≌△DEF.
A
B
C
D
E
F
其中一个三角形沿直线BC平移后,能与另一个三角形重合.
典例分析
例2 已知:如图,AB=DE,AC=DF,BE=CF.
求证:△ABC≌△DEF.
A
B
C
D
E
F
证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
∴ △ABC≌△DEF (SSS).
典例分析
变式 已知,AB=DC,DB=AC.
求证:∠ABD=∠DCA.
A
C
B
D
证明:连接AD .
在△ABD和△DCA中,
∴△ABD≌△DCA (SSS),
∴∠ABD=∠DCA.
可以连接B C吗?
新知巩固
1. 如图,四边形ABCD是正方形,连接AC. 求∠BAC的度数.
A
C
B
D
证明:∵四边形ABCD是正方形,
∴AB=BC=DC=AD,∠BAD=90°.
在△ABC和△ADC中,
∴△ABC≌△ADC (SSS),
∴∠BAC=∠DAC.
∵∠BAC+∠DAC=∠BAD=90°,
∴∠BAC=45°.
新知巩固
2. 如图,点C,D在AB上,PA=PB,AC=BD,PC=PD.
求证:△PAD≌△PBC.
证明:∵AC=BD,
∴AC+CD=BD+EC.
即AD=BC.
在△PAD和△PBC中,
∴△PAD≌△PBC.
A
P
C
B
D
新知巩固
3.已知:如图,AB=CD,AD=CB,
求证:(1)∠A=∠C;(2)AB∥DC,AD∥BC.
A
C
D
B
证明:(1)连接BD .
在△ABD和△CDB中,
∴△ABD≌△CDB.
∴∠A=∠C.
(2) ∵ △ABD≌△CDB,
∴∠ABD=∠CDB, ∠ADB=∠CBD .
∴AB∥DC,AD∥BC.
讨论交流
你知道为什么三角形框架不会变形了吗?
如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定. 三角形的这个性质叫做三角形的稳定性.
讨论交流
三角形的稳定性在生活中有广泛的应用.你能举出一些例子吗
空调外机支架
塔式起重机
讨论交流
三角形的稳定性在生活中有广泛的应用.你能举出一些例子吗
课堂小结
SSS判定
条件
三边
作图验证
应用
初步了解添加辅助线构造全等三角形
三角形的稳定性
感谢聆听!
同课章节目录
