【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第2课时角边角)课件(共15张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.3全等三角形的判定(第2课时角边角)课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 46.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:51:46 | ||
图片预览



文档简介
(共15张PPT)
1.3 全等三角形的判定
第2课时 角边角
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历探索三角形全等的条件的过程,体会分析问题的方法,积累数学活动的经验.
探索并掌握三角形全等的“角边角”条件,并能利用这个条件判定两个三角形全等,发展推理能力.
会利用基本作图作三角形:已知两角及其夹边作三角形,理解尺规作图的基本原理和方法,发展空间观念.
新知探究
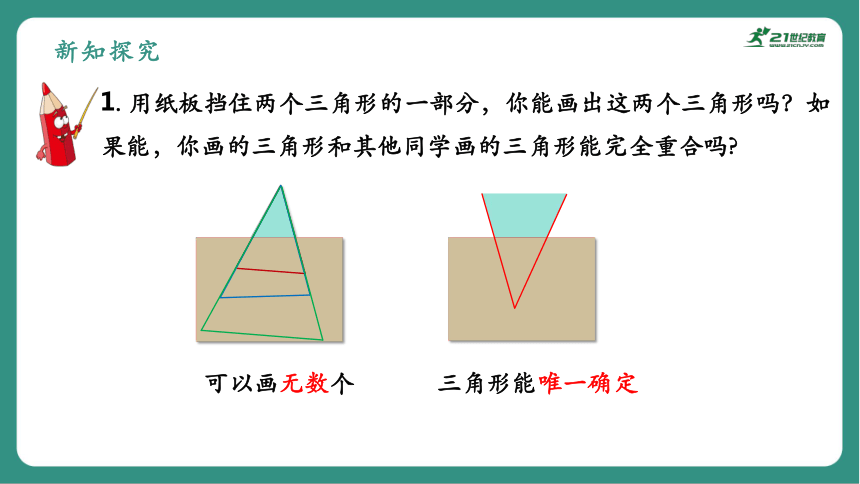
1. 用纸板挡住两个三角形的一部分,你能画出这两个三角形吗?如果能,你画的三角形和其他同学画的三角形能完全重合吗
可以画无数个
三角形能唯一确定
新知探究
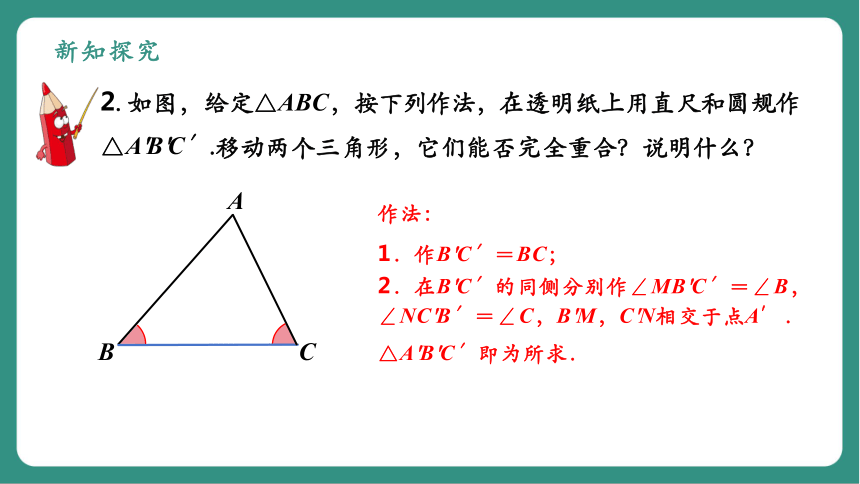
2. 如图,给定△ABC,按下列作法,在透明纸上用直尺和圆规作△A'B'C′.
作法:
1.作B'C′=BC;
2.在B'C′的同侧分别作∠MB'C′=∠B,
∠NC'B′=∠C,B'M,C'N相交于点A′.
△A'B'C′即为所求.
B
C
A
移动两个三角形,它们能否完全重合?说明什么?
新知探究
两角及其夹边分别相等的两个三角形全等.
(简写成“角边角”或“ASA”)
以上实践告诉我们判定两个三角形全等的一个基本事实:
这个基本事实可以用来判定两个三角形全等.
新知探究
\
A
B
C
\
A′
B′
C′
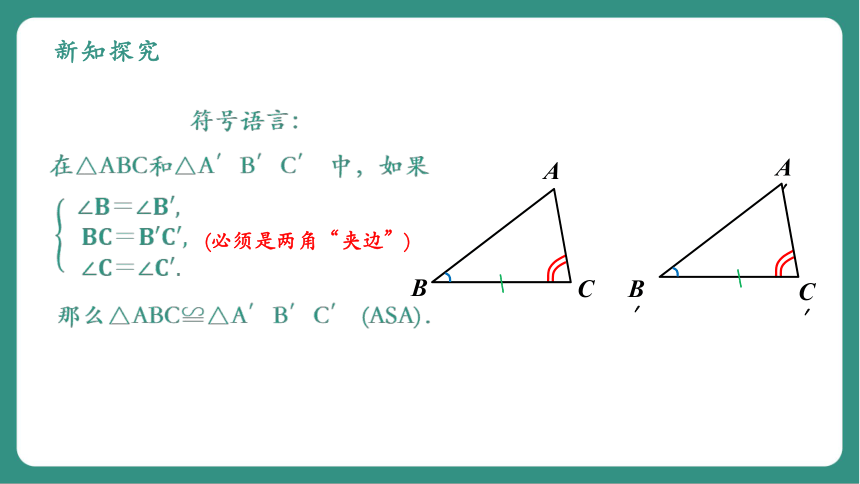
符号语言:
在△ABC和△A′B′C′ 中,如果
那么△ABC≌△A′B′C′ (ASA).
(必须是两角“夹边”)
典例分析
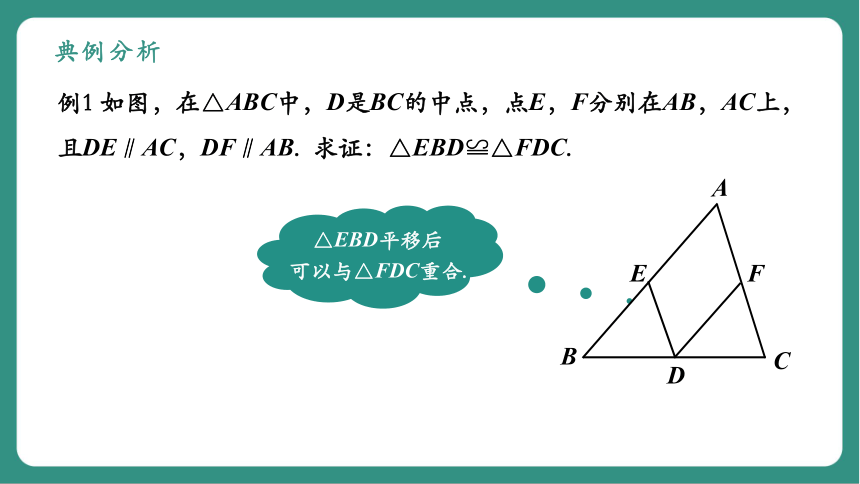
例1 如图,在△ABC中,D是BC的中点,点E,F分别在AB,AC上,且DE∥AC,DF∥AB. 求证:△EBD≌△FDC.
△EBD平移后
可以与△FDC重合.
D
A
E
B
C
F
典例分析
例1 如图,在△ABC中,D是BC的中点,点E,F分别在AB,AC上,且DE∥AC,DF∥AB. 求证:△EBD≌△FDC.
D
A
E
B
C
F
证明:∵DE∥AC,DF∥AB,
∴∠EDB=∠C,∠B=∠FDC(两直线平行,同位角相等).
∵D是BC的中点,
∴BD=DC.
在△EBD和△FDC中,
∴ △EBD≌△FDC (ASA).
典例分析
例2 如图,要测量河两岸相对的A,B两点之间的距离,可以在与AB垂直的河岸BF上取C,D两点,且使BC=DC. 从点D出发沿与河岸BF垂直的方向移动到点E,使点A,C,E在一条直线上. 测量DE的长就能知道A,B两点之间的距离. 请说明理由.
解:∵AB⊥BF,ED⊥BF(已知),
∴∠ABC=∠EDC=90°(垂直定义).
在△ABC和△EDC中,
∴△ ABC ≌△ EDC(ASA).
∴BA=DE (全等三角形的对应边相等),
∴ 测量DE的长就能知道A,B两点之间的距离.
新知巩固
1. 找出图中的全等三角形,并说明理由.
B
A
C
75°
7
25°
Y
X
Z
7
60°
50°
Q
P
R
110°
7
25°
70°
50°
7
W
S
T
F
D
E
110°
25°
60°
7
75°
25°
7
G
M
N
(1)
(2)
(3)
(4)
(5)
(6)
解:(1)和(6),(2)和(4),(3)和(5),根据基本事实“ASA”.
新知巩固
2. 如图,∠ABC=∠DCB,∠1=∠2. 求证:AB=DC.
B
A
C
1
D
2
证明:∵∠ABC=∠DCB,∠1=∠2,
∴∠ABC-∠1=∠DCB-∠2,
即∠DBC=∠ACB.
在△ABC和△DCB中,
∴ △ABC≌△DCB (ASA).
∴AB=DC.
思维提升
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
∴ △AOD≌△COB (ASA).
A
C
B
D
O
问:这位同学的回答及证明过程正确吗?为什么?
思维提升
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
解:这位同学的解法错误.
因为两角夹边对应相等的两个三角形全等.
本题中,∠A与∠AOD的夹边是OA,∠C与∠BOC的夹边是OC,
因为OA≠OC,所以不能证明两三角形全等.
A
C
B
D
O
课堂小结
ASA判定
条件
两角+夹边
作图验证
应用
找"夹边"→两角的公共边
证角等→利用平行线/对顶角等工具
感谢聆听!
1.3 全等三角形的判定
第2课时 角边角
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历探索三角形全等的条件的过程,体会分析问题的方法,积累数学活动的经验.
探索并掌握三角形全等的“角边角”条件,并能利用这个条件判定两个三角形全等,发展推理能力.
会利用基本作图作三角形:已知两角及其夹边作三角形,理解尺规作图的基本原理和方法,发展空间观念.
新知探究
1. 用纸板挡住两个三角形的一部分,你能画出这两个三角形吗?如果能,你画的三角形和其他同学画的三角形能完全重合吗
可以画无数个
三角形能唯一确定
新知探究
2. 如图,给定△ABC,按下列作法,在透明纸上用直尺和圆规作△A'B'C′.
作法:
1.作B'C′=BC;
2.在B'C′的同侧分别作∠MB'C′=∠B,
∠NC'B′=∠C,B'M,C'N相交于点A′.
△A'B'C′即为所求.
B
C
A
移动两个三角形,它们能否完全重合?说明什么?
新知探究
两角及其夹边分别相等的两个三角形全等.
(简写成“角边角”或“ASA”)
以上实践告诉我们判定两个三角形全等的一个基本事实:
这个基本事实可以用来判定两个三角形全等.
新知探究
\
A
B
C
\
A′
B′
C′
符号语言:
在△ABC和△A′B′C′ 中,如果
那么△ABC≌△A′B′C′ (ASA).
(必须是两角“夹边”)
典例分析
例1 如图,在△ABC中,D是BC的中点,点E,F分别在AB,AC上,且DE∥AC,DF∥AB. 求证:△EBD≌△FDC.
△EBD平移后
可以与△FDC重合.
D
A
E
B
C
F
典例分析
例1 如图,在△ABC中,D是BC的中点,点E,F分别在AB,AC上,且DE∥AC,DF∥AB. 求证:△EBD≌△FDC.
D
A
E
B
C
F
证明:∵DE∥AC,DF∥AB,
∴∠EDB=∠C,∠B=∠FDC(两直线平行,同位角相等).
∵D是BC的中点,
∴BD=DC.
在△EBD和△FDC中,
∴ △EBD≌△FDC (ASA).
典例分析
例2 如图,要测量河两岸相对的A,B两点之间的距离,可以在与AB垂直的河岸BF上取C,D两点,且使BC=DC. 从点D出发沿与河岸BF垂直的方向移动到点E,使点A,C,E在一条直线上. 测量DE的长就能知道A,B两点之间的距离. 请说明理由.
解:∵AB⊥BF,ED⊥BF(已知),
∴∠ABC=∠EDC=90°(垂直定义).
在△ABC和△EDC中,
∴△ ABC ≌△ EDC(ASA).
∴BA=DE (全等三角形的对应边相等),
∴ 测量DE的长就能知道A,B两点之间的距离.
新知巩固
1. 找出图中的全等三角形,并说明理由.
B
A
C
75°
7
25°
Y
X
Z
7
60°
50°
Q
P
R
110°
7
25°
70°
50°
7
W
S
T
F
D
E
110°
25°
60°
7
75°
25°
7
G
M
N
(1)
(2)
(3)
(4)
(5)
(6)
解:(1)和(6),(2)和(4),(3)和(5),根据基本事实“ASA”.
新知巩固
2. 如图,∠ABC=∠DCB,∠1=∠2. 求证:AB=DC.
B
A
C
1
D
2
证明:∵∠ABC=∠DCB,∠1=∠2,
∴∠ABC-∠1=∠DCB-∠2,
即∠DBC=∠ACB.
在△ABC和△DCB中,
∴ △ABC≌△DCB (ASA).
∴AB=DC.
思维提升
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
∴ △AOD≌△COB (ASA).
A
C
B
D
O
问:这位同学的回答及证明过程正确吗?为什么?
思维提升
阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
解:这位同学的解法错误.
因为两角夹边对应相等的两个三角形全等.
本题中,∠A与∠AOD的夹边是OA,∠C与∠BOC的夹边是OC,
因为OA≠OC,所以不能证明两三角形全等.
A
C
B
D
O
课堂小结
ASA判定
条件
两角+夹边
作图验证
应用
找"夹边"→两角的公共边
证角等→利用平行线/对顶角等工具
感谢聆听!
同课章节目录
