【新教材新课标】苏科版数学八年级上册1.2全等三角形课件(共22张PPT)
文档属性
| 名称 | 【新教材新课标】苏科版数学八年级上册1.2全等三角形课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 41.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 05:50:57 | ||
图片预览




文档简介
(共22张PPT)
1.2 全等三角形
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历三角形平移、轴对称、旋转的变化过程,认识全等三角形,发展空间观念.
理解全等三角形的概念,能识别全等三角形中的对应顶点、对应边和对应角,并会用符号表示两个三角形全等.
掌握全等三角形的性质,并能进行简单的推理和计算,发展推理能力和运算能力.
知识回顾
B
C
A
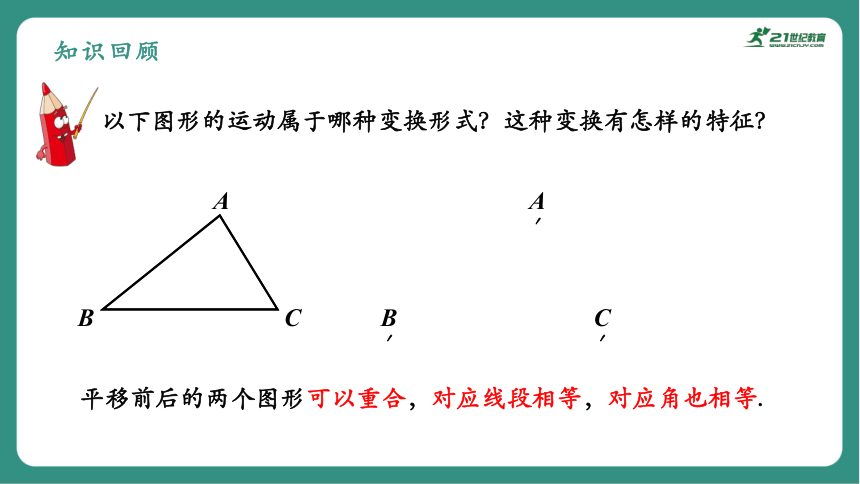
以下图形的运动属于哪种变换形式?这种变换有怎样的特征?
A′
B′
C′
平移前后的两个图形可以重合,对应线段相等,对应角也相等.
知识回顾
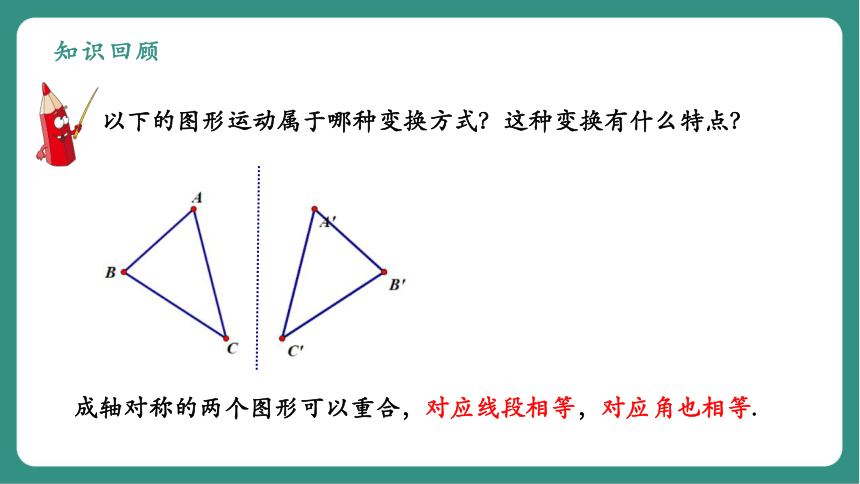
以下的图形运动属于哪种变换方式?这种变换有什么特点?
成轴对称的两个图形可以重合,对应线段相等,对应角也相等.
知识回顾
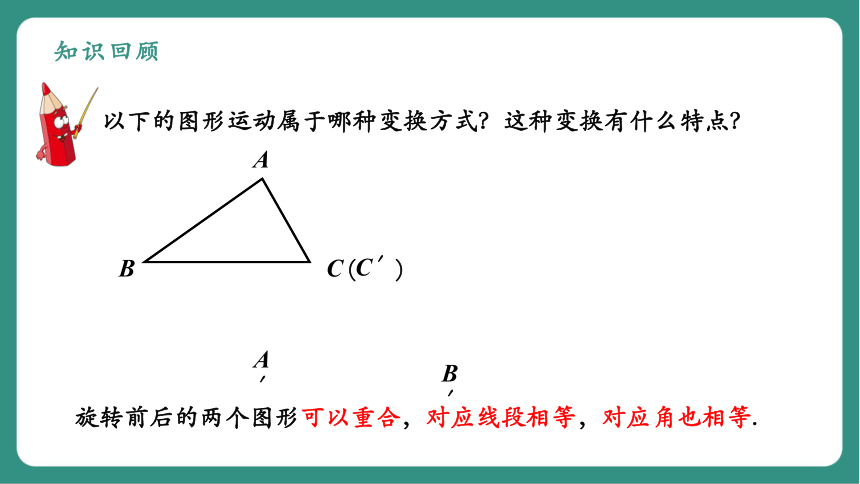
以下的图形运动属于哪种变换方式?这种变换有什么特点?
B
C
A
B′
(C′)
A′
旋转前后的两个图形可以重合,对应线段相等,对应角也相等.
概念引入
我们把两个能完全重合的三角形叫作全等三角形.
一个三角形经过平移、轴对称或旋转变换后得到另一个三角形,这两个三角形可以重合.
新知巩固
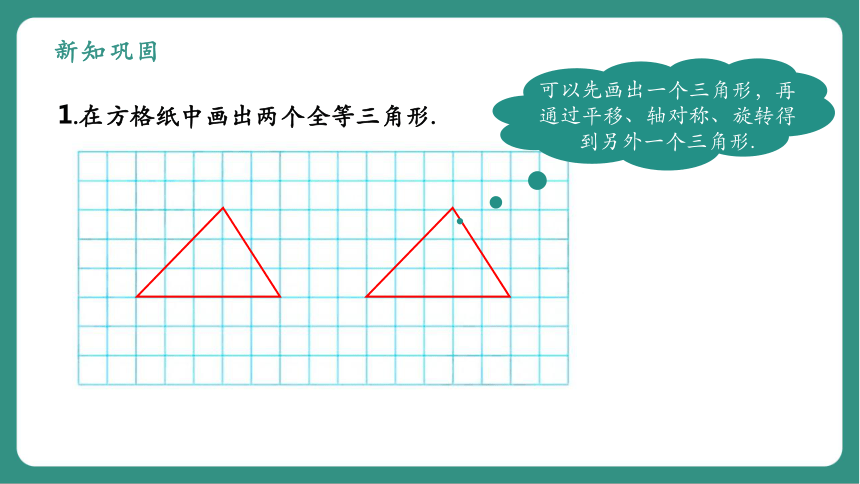
1.在方格纸中画出两个全等三角形.
可以先画出一个三角形,再通过平移、轴对称、旋转得到另外一个三角形.
新知巩固
2.把图中的等腰三角形分成两个全等三角形.
全等三角形如何表示呢?
B
C
A
新知探究
B′
C′
A′
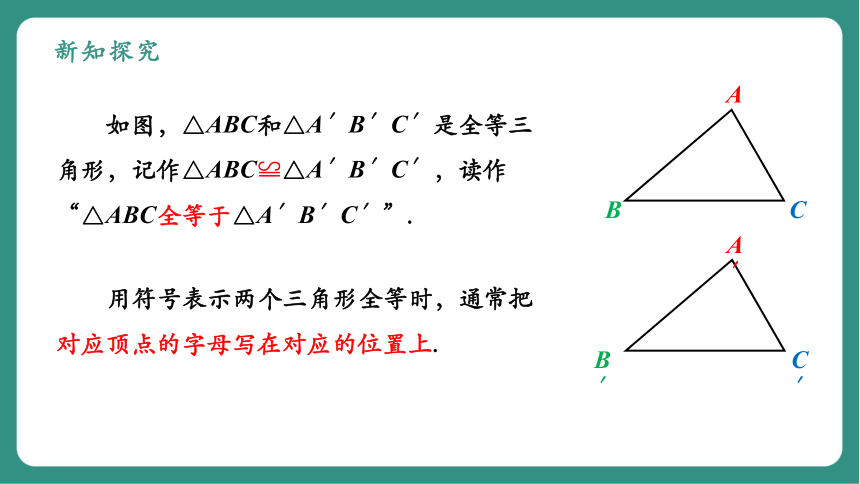
如图,△ABC和△A′B′C′是全等三角形,记作△ABC≌△A′B′C′,读作“△ABC全等于△A′B′C′”.
用符号表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
B
C
A
新知探究
B′
C′
A′
顶点A和A',B和B′,C和C′是对应顶点;
AB和A'B′,BC和B′C′,AC和A′C′是对应边;
∠A和∠A',∠B和∠B′,∠C和∠C′是对应角.
全等三角形的对应边、对应角有什么关系呢?
新知归纳
全等三角形的对应边相等,对应角相等.
全等三角形的性质:
B
C
A
B′
C′
A′
如果△ABC≌△A'B'C′,
那么 AB=A'B',AC=A'C',BC=B'C',
∠A=∠A',∠B=∠B',∠C=∠C'.
新知巩固
1. 如图,△OMQ≌△OPN,写出这两个三角形中的对应边和对应角.
Q
O
M
P
N
解:对应边为MQ和PN,MO和PO,OQ和ON;
对应角为∠M和∠P,∠Q和∠N,∠MOQ和∠PON.
新知巩固
2. 如图,△ABC≌△CDA,写出图中相等的边和角.
B
A
C
D
解:相等的边:AB=CD,AC=CA,AD=CB;
相等的角:∠BAC=∠DCA,∠B=∠D,∠ACB=∠CAD.
注意:对应顶点的字母写在对应的位置上.
典例分析
证明:∵△ABC≌△EFD,
∴ ∠B=∠F (全等三角形的对应角相等).
∴ AB∥EF (内错角相等,两直线平行).
例1 如图,已知△ABC≌△EFD.
求证:AB∥EF.
B
A
C
E
D
F
典例分析
变式 如图,当△DEF沿BC所在直线平移时,你可以找到哪些始终保持平行的直线?
B
A
C
E
D
F
始终保持平行的直线有
DE与AC,
EF与AB.
典例分析
例2 如图,△ABE≌△ACF,点E在AC上,点F在AB上.
(1)判断BF与CE是否相等,并证明你的结论;
B
O
F
A
E
C
证明:(1) BF=CE,理由如下,
∵△ABE≌△ACF,
∴ AB=AC ,AE=AF
(全等三角形的对应边相等).
∵BF=AB-AF,CE=AC-AE,
∴ BF=CE .
典例分析
例2 如图,△ABE≌△ACF,点E在AC上,点F在AB上.
(2)判断∠BFO与∠CEO是否相等,并证明你的结论.
B
O
F
A
E
C
证明:(2)∠BFO=∠CEO,理由如下,
∵△ABE≌△ACF,
∴ ∠B=∠C (全等三角形的对应角相等).
∵∠BFO=∠A+∠C,
∠CEO=∠A+∠B,
∴ ∠BFO=∠CEO.
新知巩固
1. 如图,△ABC≌△DCB,AC与BD相交于点E,若∠ACB=40°,求∠BEC的度数.
C
B
A
D
E
解:∵△ABC≌△DCB,∠ACB=40°,
∴∠DBC=∠ACB=40°.
∴∠BEC=180°-∠DBC-∠ACB
=180°-40°-40°
=100°.
2. 如图,△ABC≌△DBC,∠A=45°,∠ACD=76°. 求△BCD各内角的度数.
新知巩固
C
B
A
D
解:∵△ABC≌△DBC,∠A=45°,
∴∠ACB=∠DCB ,∠D=∠A=45°,
∵∠ACD=76°,
∴∠DCB=∠ACD=×76°=38°,
∴∠CBD=180°-∠D-∠DCB
=180°-45°-38 °
=97°.
新知巩固
3. 如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边,
∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B=35°,AB=3cm,
BC=1cm,求出∠E、∠ ADE的度数和线段DE、AE 的长度.
B
C
E
D
A
解:∵ △ABC≌△AED (已知),
∴∠E=∠B=35°(全等三角形对应角相等).
∠ADE=∠ACB=180°-25°-35°=120 °, (全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm.
(全等三角形对应边相等)
课堂小结
全等三角形
定义
两个能完全重合的三角形
表示方法
“≌”读作“全等于”
有关概念
对应顶点、对应边、对应角
性质
对应边相等、对应角相等
感谢聆听!
1.2 全等三角形
第一章 三角形
苏科版数学(新教材)八年级上册
学 习 目 标
1
2
3
经历三角形平移、轴对称、旋转的变化过程,认识全等三角形,发展空间观念.
理解全等三角形的概念,能识别全等三角形中的对应顶点、对应边和对应角,并会用符号表示两个三角形全等.
掌握全等三角形的性质,并能进行简单的推理和计算,发展推理能力和运算能力.
知识回顾
B
C
A
以下图形的运动属于哪种变换形式?这种变换有怎样的特征?
A′
B′
C′
平移前后的两个图形可以重合,对应线段相等,对应角也相等.
知识回顾
以下的图形运动属于哪种变换方式?这种变换有什么特点?
成轴对称的两个图形可以重合,对应线段相等,对应角也相等.
知识回顾
以下的图形运动属于哪种变换方式?这种变换有什么特点?
B
C
A
B′
(C′)
A′
旋转前后的两个图形可以重合,对应线段相等,对应角也相等.
概念引入
我们把两个能完全重合的三角形叫作全等三角形.
一个三角形经过平移、轴对称或旋转变换后得到另一个三角形,这两个三角形可以重合.
新知巩固
1.在方格纸中画出两个全等三角形.
可以先画出一个三角形,再通过平移、轴对称、旋转得到另外一个三角形.
新知巩固
2.把图中的等腰三角形分成两个全等三角形.
全等三角形如何表示呢?
B
C
A
新知探究
B′
C′
A′
如图,△ABC和△A′B′C′是全等三角形,记作△ABC≌△A′B′C′,读作“△ABC全等于△A′B′C′”.
用符号表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
B
C
A
新知探究
B′
C′
A′
顶点A和A',B和B′,C和C′是对应顶点;
AB和A'B′,BC和B′C′,AC和A′C′是对应边;
∠A和∠A',∠B和∠B′,∠C和∠C′是对应角.
全等三角形的对应边、对应角有什么关系呢?
新知归纳
全等三角形的对应边相等,对应角相等.
全等三角形的性质:
B
C
A
B′
C′
A′
如果△ABC≌△A'B'C′,
那么 AB=A'B',AC=A'C',BC=B'C',
∠A=∠A',∠B=∠B',∠C=∠C'.
新知巩固
1. 如图,△OMQ≌△OPN,写出这两个三角形中的对应边和对应角.
Q
O
M
P
N
解:对应边为MQ和PN,MO和PO,OQ和ON;
对应角为∠M和∠P,∠Q和∠N,∠MOQ和∠PON.
新知巩固
2. 如图,△ABC≌△CDA,写出图中相等的边和角.
B
A
C
D
解:相等的边:AB=CD,AC=CA,AD=CB;
相等的角:∠BAC=∠DCA,∠B=∠D,∠ACB=∠CAD.
注意:对应顶点的字母写在对应的位置上.
典例分析
证明:∵△ABC≌△EFD,
∴ ∠B=∠F (全等三角形的对应角相等).
∴ AB∥EF (内错角相等,两直线平行).
例1 如图,已知△ABC≌△EFD.
求证:AB∥EF.
B
A
C
E
D
F
典例分析
变式 如图,当△DEF沿BC所在直线平移时,你可以找到哪些始终保持平行的直线?
B
A
C
E
D
F
始终保持平行的直线有
DE与AC,
EF与AB.
典例分析
例2 如图,△ABE≌△ACF,点E在AC上,点F在AB上.
(1)判断BF与CE是否相等,并证明你的结论;
B
O
F
A
E
C
证明:(1) BF=CE,理由如下,
∵△ABE≌△ACF,
∴ AB=AC ,AE=AF
(全等三角形的对应边相等).
∵BF=AB-AF,CE=AC-AE,
∴ BF=CE .
典例分析
例2 如图,△ABE≌△ACF,点E在AC上,点F在AB上.
(2)判断∠BFO与∠CEO是否相等,并证明你的结论.
B
O
F
A
E
C
证明:(2)∠BFO=∠CEO,理由如下,
∵△ABE≌△ACF,
∴ ∠B=∠C (全等三角形的对应角相等).
∵∠BFO=∠A+∠C,
∠CEO=∠A+∠B,
∴ ∠BFO=∠CEO.
新知巩固
1. 如图,△ABC≌△DCB,AC与BD相交于点E,若∠ACB=40°,求∠BEC的度数.
C
B
A
D
E
解:∵△ABC≌△DCB,∠ACB=40°,
∴∠DBC=∠ACB=40°.
∴∠BEC=180°-∠DBC-∠ACB
=180°-40°-40°
=100°.
2. 如图,△ABC≌△DBC,∠A=45°,∠ACD=76°. 求△BCD各内角的度数.
新知巩固
C
B
A
D
解:∵△ABC≌△DBC,∠A=45°,
∴∠ACB=∠DCB ,∠D=∠A=45°,
∵∠ACD=76°,
∴∠DCB=∠ACD=×76°=38°,
∴∠CBD=180°-∠D-∠DCB
=180°-45°-38 °
=97°.
新知巩固
3. 如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边,
∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B=35°,AB=3cm,
BC=1cm,求出∠E、∠ ADE的度数和线段DE、AE 的长度.
B
C
E
D
A
解:∵ △ABC≌△AED (已知),
∴∠E=∠B=35°(全等三角形对应角相等).
∠ADE=∠ACB=180°-25°-35°=120 °, (全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm.
(全等三角形对应边相等)
课堂小结
全等三角形
定义
两个能完全重合的三角形
表示方法
“≌”读作“全等于”
有关概念
对应顶点、对应边、对应角
性质
对应边相等、对应角相等
感谢聆听!
同课章节目录
