第二十一章一元二次方程 章末过关检测试题 2025-2026学年上期初中数学人教版九年级上册
文档属性
| 名称 | 第二十一章一元二次方程 章末过关检测试题 2025-2026学年上期初中数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 837.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 11:40:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十一章一元二次方程 章末过关检测试题
2025-2026学年上期初中数学人教版九年级上册
一、单选题
1.对于关于的一元二次方程,下列说法:
①若,则;
②若关于的方程有两个不相等的实根,则方程必有两个不相等的实数根;
③若是方程的一个根,则;
其中所有正确说法的序号是( )
A.① B.①② C.①③ D.①②③
2.定义新运算:.若方程有两个相等正实数根,且(其中),则的值为( )
A. B.4 C. D.2
3.已知和是方程的两个解,则的值为( )
A. B.2023 C. D.2021
4.某服装店购进一款印有“龘”字图案的上衣,据店长统计,该款上衣1月份销售量为150件,3月份销售量为216件,则该款上衣销售量的月平均增长率为( )
A. B. C. D.
5.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,…,第n行有n个点,…,前n行的点数和不能是以下哪个结果( )
A.820 B.600 C.465 D.210
6.若两数的差为4,且它们的积为45,则这两个数为( )
A.,9 B.,5 C.9,5 D.,或9,5
7.已知、是方程的两根,且,则的值等于
A. B. C. D.
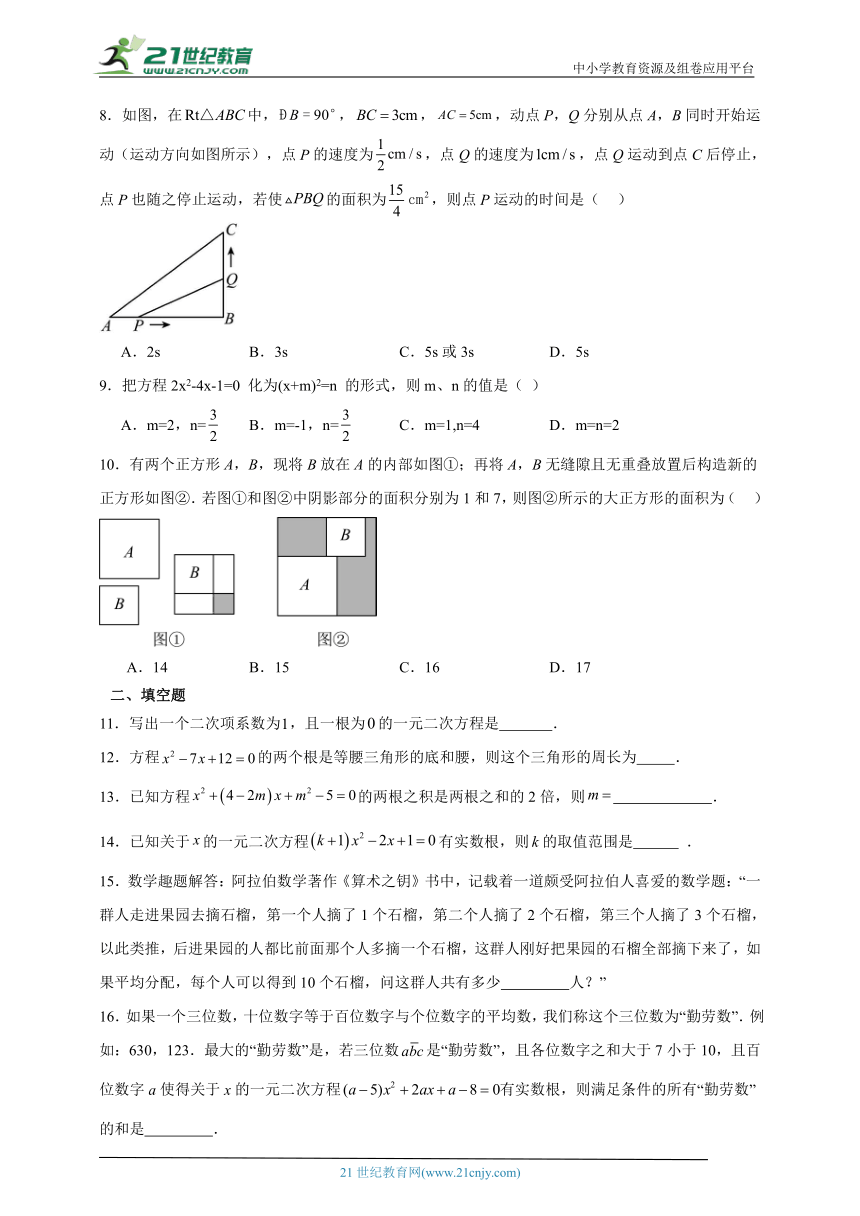
8.如图,在中,,,,动点P,Q分别从点A,B同时开始运动(运动方向如图所示),点P的速度为,点Q的速度为,点Q运动到点C后停止,点P也随之停止运动,若使的面积为,则点P运动的时间是( )
A.2s B.3s C.5s或3s D.5s
9.把方程2x2-4x-1=0 化为(x+m)2=n 的形式,则m、n的值是( )
A.m=2,n= B.m=-1,n= C.m=1,n=4 D.m=n=2
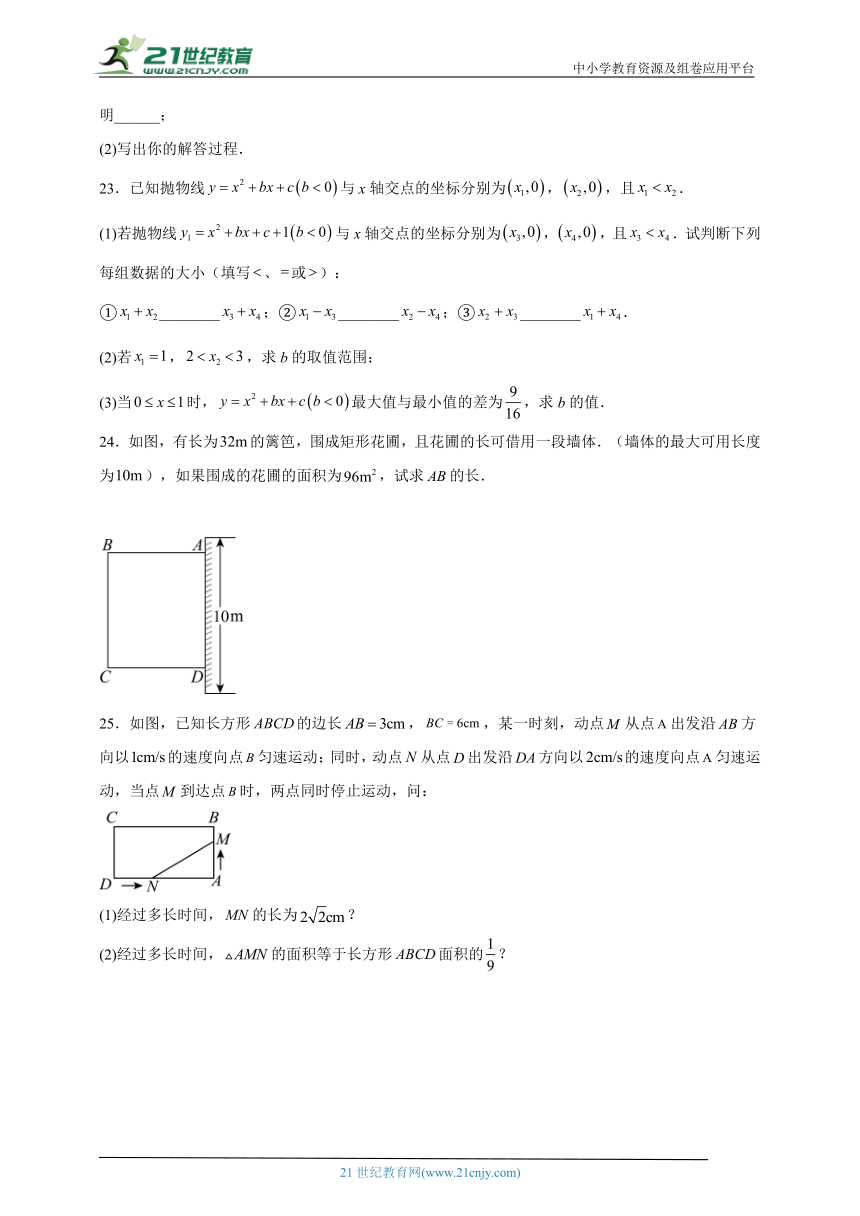
10.有两个正方形A,B,现将B放在A的内部如图①;再将A,B无缝隙且无重叠放置后构造新的正方形如图②.若图①和图②中阴影部分的面积分别为1和7,则图②所示的大正方形的面积为( )
A.14 B.15 C.16 D.17
二、填空题
11.写出一个二次项系数为,且一根为的一元二次方程是 .
12.方程的两个根是等腰三角形的底和腰,则这个三角形的周长为 .
13.已知方程的两根之积是两根之和的2倍,则 .
14.已知关于的一元二次方程有实数根,则的取值范围是 .
15.数学趣题解答:阿拉伯数学著作《算术之钥》书中,记载着一道颇受阿拉伯人喜爱的数学题:“一群人走进果园去摘石榴,第一个人摘了1个石榴,第二个人摘了2个石榴,第三个人摘了3个石榴,以此类推,后进果园的人都比前面那个人多摘一个石榴,这群人刚好把果园的石榴全部摘下来了,如果平均分配,每个人可以得到10个石榴,问这群人共有多少 人?”
16.如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“勤劳数”.例如:630,123.最大的“勤劳数”是,若三位数是“勤劳数”,且各位数字之和大于7小于10,且百位数字a使得关于x的一元二次方程有实数根,则满足条件的所有“勤劳数”的和是 .
三、解答题
17.用合适的方法解方程:
(1);
(2);
(3);
(4).
18.若一元二次方程的右边被墨水污染▊.
(1)若方程的一个解为时,求“▊”的值;
(2)若“▊”表示,求.
19.已知关于的方程
(1)求证:无论取何值,原方程总有两个不相等的实数根.
(2)若方程的一个根是1,求的值及方程的另一个根 .
20.已知关于的一元二次方程.
(1)求证:无论为何值,该方程总有两个不等实根.
(2)当的斜边,且两直角边恰好是这个方程的两个根,求的值.
21.某网店以每件40元的价格购进一批商品,若以单价50元销售,每月可售出200件,调查表明:单价每上涨1元,该商品每月的销售量就减少10件.为了尽可能的减少快递支出,网店决定采取适当的涨价措施.设每件商品涨价x元.据此规律,请回答:
(1)该网店月销售量减少_______件,每件商品盈利________元(用含x的代数式表示);
(2)在上述条件下,每件商品售价多少元时,网店月盈利可达到2000元?
22.小颖与小明两位同学解方程过程如下框:
小颖: 两边同除以,得. 小明: 移项,得, 提取公因式,得. 所以,或, 解得,.
(1)你认为他们的过程是否正确?若正确请在括号内打“√”;若错误请在括号内打“×”:小颖______,小明______;
(2)写出你的解答过程.
23.已知抛物线与x轴交点的坐标分别为,,且.
(1)若抛物线与x轴交点的坐标分别为,,且.试判断下列每组数据的大小(填写、或):
①________;②________;③________.
(2)若,,求b的取值范围;
(3)当时,最大值与最小值的差为,求b的值.
24.如图,有长为的篱笆,围成矩形花圃,且花圃的长可借用一段墙体.(墙体的最大可用长度为),如果围成的花圃的面积为,试求的长.
25.如图,已知长方形的边长,,某一时刻,动点从点出发沿方向以的速度向点匀速运动;同时,动点从点出发沿方向以的速度向点匀速运动,当点到达点时,两点同时停止运动,问:
(1)经过多长时间,的长为?
(2)经过多长时间,的面积等于长方形面积的?
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C A B D C B B B
1.B
【分析】本题主要考查了一元二次方程根的判别式,一元二次方程的根,
将代入计算判断①;再根据方程有两个不相等的实数根可得,然后根据一元二次方程根的判别式解答②;接下来将代入方程可知,可解答③.
【详解】解:∵,
∴,
∴.
所以①正确;
∵方程有两个不相等的实数根,
∴.
方程中,
∴该方程有两个不相等的实数根.
所以②正确;
将代入方程,
可得,
∴.
所以③不正确.
正确的有①②.
故选:B.
2.B
【分析】本题考查了根的判别式,一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.根据判别式的意义得到,解得,,再利用方程有两个相等的正实数解,所以,则.利用新定义得到,然后整理后利用因式分解得到,从而得到的值.
【详解】解:∵方程有两个相等实数根,
∴,
解得,,
当时方程有两个相等的负实数解,
∴,
∵,
∴,
整理得,
,
而,
∴,
即.
故选:B.
3.C
【分析】本题考查了根与系数的关系的运用,由根与系数的关系可以求出,,然后变形为,再整体代入可以求出其值.
【详解】解:∵和是方程的两个解,
∴,,
∴,
∴
,
故选:C.
4.A
【分析】本题考查了列一元二次方程,找准等量关系、正确列出方程是解题的关键.
该款上衣销售量的月平均增长率为,根据3月份销售量和1月份销售量列出一元二次方程求解即可.
【详解】解:该款上衣销售量的月平均增长率为,
由题意可得:,
解得:或不合题意舍弃,
所以该款上衣销售量的月平均增长率为.
故选A.
5.B
【分析】本题考查了一元二次方方程的应用,先求出前行的点数之和,再分别求出该代数式的值分别为、600、465、210时的值,判断即可得解.
【详解】解:由题意可得:前行的点数之和为,
若前行的点数之和为,则,
解得:(舍去)或,即前行的点数之和为,故A不符合题意;
若前行的点数之和为600,则,
解得:,不是整数,即不存在前行的点数之和为600,故B符合题意;
若前行的点数之和为465,则,
解得:或(舍去),即前行的点数之和为465,故C不符合题意;
若前行的点数之和为210,则,
解得:或(舍去),即前行的点数之和为210,故D不符合题意;
故选:B.
6.D
【分析】设较小的数为x,那么较大的数应该为,根据“积为45”可得出:,解方程即可求得这两个数.
【详解】解:设较小的数为x,根据题意得,
解得,.
那么这两个数就应该是5,9或,.
故选:D
【点睛】本题考查了一元二次方程的应用,解题关键是根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
7.C
【详解】试题解析:∵m,n是方程x2﹣2x﹣1=0的两根
∴m2﹣2m=1,n2﹣2n=1
∴7m2﹣14m=7(m2﹣2m)=7,3n2﹣6n=3(n2﹣2n)=3
∵(7m2﹣14m+a)(3n2﹣6n﹣7)=8
∴(7+a)×(﹣4)=8
∴a=﹣9.
故选C.
8.B
【分析】先求解,设运动时间为,可得,,再利用面积建立方程求解即可.
【详解】解:∵,,,
∴,
设运动时间为,
∴,,
∵的面积为,即
,解得:,.
当时,,不成立,舍去,
∴,
故选B.
【点睛】本题考查的是一元二次方程的应用,勾股定理的应用,理解题意,熟练的建立方程求解是解本题的关键.
9.B
【详解】解:∵2x2﹣4x﹣1=0,∴2x2﹣4x=1,∴x2﹣2x=,∴x2﹣2x+1=+1,∴(x﹣1)2=,∴m=﹣1,n=.故选B.
10.B
【分析】此题主要考查了正方形的性质,准确识图,熟练掌握正方形的性质,并根据正方形的面积公式构造方程是解决问题的关键.设正方形B的边长为a,其中,依题意由图①得阴影部分为正方形,且边长为1,则正方形A的边长为,依题意得图②中大正方形的边长为,则,由此解出,进而再求出图②中大正方形的面积即可.
【详解】解:设正方形B的边长为a,其中,
∵将B放在A的内部如图①所示,阴影部分的面积为1,
∴阴影部分为正方形,且边长为1,
∴图①中大正方形的边长为,
即正方形A的边长为,
又∵将A,B无缝隙且无重叠放置后构造新的正方形如图②所示:
∴图②中大正方形的边长为:,
∵图②中阴影部分的面积为7,
∴,
整理得:,
解得:,(不合题意,舍去),
∴图②中大正方形的边长为:
∴图②中大正方形的面积为15.
故选:B.
11.(答案不唯一)
【分析】本题主要考查了一元二次方程的一般形式,熟练掌握一元二次方程的一般形式是解答本题的关键.根据一元二次方程的一般形式写出符合题意的方程即可.
【详解】解:由题意知二次项系数为,且一根为的一元二次方程可以是,
故答案为:(答案不唯一).
12.10或11
【分析】此题考查了解一元二次方程因式分解法,等腰三角形的定义,利用因式分解法求出方程的解得到的值,确定出底与腰,即可求出周长.熟练掌握因式分解法是解本题的关键.
【详解】解:,
,
解得:,,
若3为底,4为腰,三角形三边为3,4,4,周长为;
若3为腰,4为底,三角形三边为3,3,4,周长为.
则这个三角形的周长为10或11,
故答案为:10或11.
13.1
【分析】本题考查了一元二次方程的根与系数的关系和一元二次方程的根的判别式等知识,属于常考题型,熟练掌握一元二次方程的基本知识是解题关键.根据一元二次方程的根与系数的关系可得,解方程即可求出m的值,再代入原方程检验即得答案.
【详解】解:设方程的两个根分别为,,
则,,
根据题意得:,即,
解得或;
当时,原方程为,;
当时,原方程为,,舍去.
∴.
故答案为:1.
14.且
【分析】本题考查了一元二次方程的定义,一元二次方程根的判别式,由题意可得且,解不等式即可求解,掌握以上知识点是解题的关键.
【详解】解:由题意得,且,
解得且,
故答案为:且.
15.19
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
设这群人共有x人,则共摘了个石榴,根据“如果平均分配,每个人可以得到10个石榴”,可列出关于x的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】解:设这群人共有x人,则共摘了个石榴,
根据题意得:,
整理得:,
解得:(不符合题意,舍去),,
∴这群人共有19人.
故答案为:19.
16.
【分析】本题考查根的判别式,根据题意正确找出等量关系列式计算是解决本题的关键.
根据“百位数字使得一元二次方程有实数根”,得到列出关于的不等式,解之得到的取值范围,根据“各位数字之和大于小于得出各位数字之和为或,集合“勤劳数”的定义,分情况讨论可能的数,从而得到对应的“勤劳数”.
【详解】解:根据题意得:,
解得:
∵各位数字之和大于小于,
或,
又∵,
(舍去)或,
若则,该数为,
若则,该数为,
答: 这个“勤劳数” 432或630,
满足条件的所有“勤劳数”的和是,
故答案为:.
17.(1),
(2),
(3)
(4)
【分析】本题考查解一元二次方程,解答此类问题的关键是根据方程的特点,选取合适的方法解方程.
(1)直接利用开方法求解即可;
(2)根据公式法可以解答此方程;
(3)先移项,根据因式分解法可以解答此方程;
(4)先移项,然后根据因式分解法解答此方程.
【详解】(1)解:
或,
解得:,;
(2)解:,
,,,
,
,
,;
(3)解:,
,
,
,
,
解得:;
(4)解:,
,
,
,
解得:.
18.(1)
(2),
【分析】本题考查一元二次方程的解与解一元二次方程,解题的关键是掌握一元二次方程的解,解一元二次方程的方法.
(1)把代入,解出▊,即可;
(2)根据题意,可得方程为,解出方程,即可.
【详解】(1)解:把代入,
∴,
∴“▊”的值为.
(2)解:由题意得,方程为,
∴,
∵,
∴,
∴,.
19.(1)见解析
(2),方程的另一个根为
【分析】本题考查了一元二次方程根的判别式以及根与系数的关系,熟练掌握以上知识点是解题的关键.
(1)根据根的判别式的符号来判定该方程的根的情况;
(2)设方程的另外一个根为,利用根与系数的关系列出关于和的二元一次方程组,解之即可得到答案.
【详解】(1)证明:
无论取何值,原方程总有两个不相等的实数根.
(2)解:设方程的另外一个根为,则
解得:,
故的值为,方程的另一个根为.
20.(1)见解析
(2)
【分析】本题考查了一元二次方程根与系数的关系和根的判别式及勾股定理,解题的关键是掌握相关知识.
(1)根据即可证明无论取什么实数值,该方程总有两个不相等的实数根;
(2)根据勾股定理及根与系数的关系列出关于的方程,解出即可得出答案.
【详解】(1)解:关于的一元二次方程,
,
,
,
无论为何值,,
无论为何值,该方程总有两个不等实根;
(2)解:和恰好是方程的两个根,
,,
是直角三角形,斜边为,
,
,
,
化简得,
解得或,
又时,,不合题意舍去,
.
21.(1)10x,10+x;
(2)每件商品售价为60元时,网店月盈利可达到2000元.
【分析】(1)根据题中已知条件“每件40元的价格购进一批商品,若以单价50元销售,每月可售出200件,调查表明:单价每上涨1元,该商品每月的销售量就减少10件”即可表示;
(2)利用销量×每件的利润=总利润列方程求解即可.
【详解】(1)解:由题意每件商品涨价x元,销量减少10x件,
每件盈利:50-40+x=(10+x)元,
故答案为:10x,10+x;
(2)解:设每件商品涨价x元,网店月盈利可达到2000元,
则,
解得:(舍去)
售价为50+10=60(元),
即每件商品售价为60元时,网店月盈利可达到2000元.
【点睛】本题考查一元二次方程的应用,根据题意找到等量关系列方程是解题的关键.
22.(1)×,×
(2)见解析
【分析】本题考查了因式分解法解一元二次方程.熟练掌握因式分解法解一元二次方程是解题的关键.
(1)根据因式分解法解一元二次方程判断即可;
(2)根据因式分解法解一元二次方程求解即可.
【详解】(1)解:由题意知,小颖×,小明×,
故答案为:×,×;
(2)解:,
,
,
∴或,
解得,,.
23.(1);;;
(2)
(3)b的值为或.
【分析】本题考查根与系数的关系,二次函数图像与性质,不等式性质,二次函数最值情况,解题的关键在于熟练掌握二次函数图像与性质.
(1)根据根与系数的关系得到,以及,即可判断①,利用二次函数的图像与性质得到,进而得到,利用不等式性质变形,即可判断②③.
(2)根据题意得到,结合进行求解,即可解题;
(3)根据题意得到抛物线顶点坐标为,对称轴为;当时,,当时,,由最大值与最小值的差为,分以下三种情况:①当在取得最大值,在取得最小值时,②当在取得最大值,在顶点取得最小值时,③当在取得最大值,在顶点取得最小值时,建立等式求解,即可解题.
【详解】(1)解: 与x轴交点的坐标分别为,,且,
,且抛物线开口向上,
与x轴交点的坐标分别为,,且.
即向上平移1个单位,
,且,
①;
,
,即②;
,即③.
故答案为;;;;
(2)解:,,
,
,
;
(3)解:抛物线顶点坐标为,
对称轴为;
当时,,
当时,,
①当,则,
那么,在取得最大值,在取得最小值时,
有,解得(不符合题意,舍去);
②当,解得,
那么,在取得最大值,在顶点取得最小值时,
有,解得(不符合题意,舍去)或,
③当,解得,
那么,在取得最大值,在顶点取得最小值时,
有,解得(不符合题意,舍去)或;
综上所述,b的值为或.
24.的长为12米
【分析】本题考查了二次函数的应用,根据题意列出函数关系式是解答本类题目的关键.设的长为,则,根据围成的花圃的面积为建立方程求解,排除不符合实际的解,即可得出结果.
【详解】解:设的长为,则,
由已知,,
则
依据题意列方程得:,
解得:(舍),
答:的长为12米.
25.(1)经过或之后,的长为cm;
(2)秒或秒.
【分析】本题考查了一元二次方程的应用,勾股定理,熟练掌握知识点的应用是解题的关键.
()设经过后,则,,,然后由勾股定理列出方程,然后解方程即可;
()设经过秒,由题意得,,,由的面积等于长方形面积的,列出方程,然后解方程即可;
【详解】(1)设经过后,则,,,的长为cm,
根据题意,由勾股定理得:,
即,
解得:,,
答:经过或之后,的长为cm;
(2)设经过秒,的面积等于矩形面积的,
由题意得,,,
∵矩形中,,,
∴,,
∴矩形的面积为:,
∴的面积,
整理得:,
解得,,
答:经过秒或秒,的面积等于长方形面积的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十一章一元二次方程 章末过关检测试题
2025-2026学年上期初中数学人教版九年级上册
一、单选题
1.对于关于的一元二次方程,下列说法:
①若,则;
②若关于的方程有两个不相等的实根,则方程必有两个不相等的实数根;
③若是方程的一个根,则;
其中所有正确说法的序号是( )
A.① B.①② C.①③ D.①②③
2.定义新运算:.若方程有两个相等正实数根,且(其中),则的值为( )
A. B.4 C. D.2
3.已知和是方程的两个解,则的值为( )
A. B.2023 C. D.2021
4.某服装店购进一款印有“龘”字图案的上衣,据店长统计,该款上衣1月份销售量为150件,3月份销售量为216件,则该款上衣销售量的月平均增长率为( )
A. B. C. D.
5.如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,…,第n行有n个点,…,前n行的点数和不能是以下哪个结果( )
A.820 B.600 C.465 D.210
6.若两数的差为4,且它们的积为45,则这两个数为( )
A.,9 B.,5 C.9,5 D.,或9,5
7.已知、是方程的两根,且,则的值等于
A. B. C. D.
8.如图,在中,,,,动点P,Q分别从点A,B同时开始运动(运动方向如图所示),点P的速度为,点Q的速度为,点Q运动到点C后停止,点P也随之停止运动,若使的面积为,则点P运动的时间是( )
A.2s B.3s C.5s或3s D.5s
9.把方程2x2-4x-1=0 化为(x+m)2=n 的形式,则m、n的值是( )
A.m=2,n= B.m=-1,n= C.m=1,n=4 D.m=n=2
10.有两个正方形A,B,现将B放在A的内部如图①;再将A,B无缝隙且无重叠放置后构造新的正方形如图②.若图①和图②中阴影部分的面积分别为1和7,则图②所示的大正方形的面积为( )
A.14 B.15 C.16 D.17
二、填空题
11.写出一个二次项系数为,且一根为的一元二次方程是 .
12.方程的两个根是等腰三角形的底和腰,则这个三角形的周长为 .
13.已知方程的两根之积是两根之和的2倍,则 .
14.已知关于的一元二次方程有实数根,则的取值范围是 .
15.数学趣题解答:阿拉伯数学著作《算术之钥》书中,记载着一道颇受阿拉伯人喜爱的数学题:“一群人走进果园去摘石榴,第一个人摘了1个石榴,第二个人摘了2个石榴,第三个人摘了3个石榴,以此类推,后进果园的人都比前面那个人多摘一个石榴,这群人刚好把果园的石榴全部摘下来了,如果平均分配,每个人可以得到10个石榴,问这群人共有多少 人?”
16.如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“勤劳数”.例如:630,123.最大的“勤劳数”是,若三位数是“勤劳数”,且各位数字之和大于7小于10,且百位数字a使得关于x的一元二次方程有实数根,则满足条件的所有“勤劳数”的和是 .
三、解答题
17.用合适的方法解方程:
(1);
(2);
(3);
(4).
18.若一元二次方程的右边被墨水污染▊.
(1)若方程的一个解为时,求“▊”的值;
(2)若“▊”表示,求.
19.已知关于的方程
(1)求证:无论取何值,原方程总有两个不相等的实数根.
(2)若方程的一个根是1,求的值及方程的另一个根 .
20.已知关于的一元二次方程.
(1)求证:无论为何值,该方程总有两个不等实根.
(2)当的斜边,且两直角边恰好是这个方程的两个根,求的值.
21.某网店以每件40元的价格购进一批商品,若以单价50元销售,每月可售出200件,调查表明:单价每上涨1元,该商品每月的销售量就减少10件.为了尽可能的减少快递支出,网店决定采取适当的涨价措施.设每件商品涨价x元.据此规律,请回答:
(1)该网店月销售量减少_______件,每件商品盈利________元(用含x的代数式表示);
(2)在上述条件下,每件商品售价多少元时,网店月盈利可达到2000元?
22.小颖与小明两位同学解方程过程如下框:
小颖: 两边同除以,得. 小明: 移项,得, 提取公因式,得. 所以,或, 解得,.
(1)你认为他们的过程是否正确?若正确请在括号内打“√”;若错误请在括号内打“×”:小颖______,小明______;
(2)写出你的解答过程.
23.已知抛物线与x轴交点的坐标分别为,,且.
(1)若抛物线与x轴交点的坐标分别为,,且.试判断下列每组数据的大小(填写、或):
①________;②________;③________.
(2)若,,求b的取值范围;
(3)当时,最大值与最小值的差为,求b的值.
24.如图,有长为的篱笆,围成矩形花圃,且花圃的长可借用一段墙体.(墙体的最大可用长度为),如果围成的花圃的面积为,试求的长.
25.如图,已知长方形的边长,,某一时刻,动点从点出发沿方向以的速度向点匀速运动;同时,动点从点出发沿方向以的速度向点匀速运动,当点到达点时,两点同时停止运动,问:
(1)经过多长时间,的长为?
(2)经过多长时间,的面积等于长方形面积的?
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C A B D C B B B
1.B
【分析】本题主要考查了一元二次方程根的判别式,一元二次方程的根,
将代入计算判断①;再根据方程有两个不相等的实数根可得,然后根据一元二次方程根的判别式解答②;接下来将代入方程可知,可解答③.
【详解】解:∵,
∴,
∴.
所以①正确;
∵方程有两个不相等的实数根,
∴.
方程中,
∴该方程有两个不相等的实数根.
所以②正确;
将代入方程,
可得,
∴.
所以③不正确.
正确的有①②.
故选:B.
2.B
【分析】本题考查了根的判别式,一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.根据判别式的意义得到,解得,,再利用方程有两个相等的正实数解,所以,则.利用新定义得到,然后整理后利用因式分解得到,从而得到的值.
【详解】解:∵方程有两个相等实数根,
∴,
解得,,
当时方程有两个相等的负实数解,
∴,
∵,
∴,
整理得,
,
而,
∴,
即.
故选:B.
3.C
【分析】本题考查了根与系数的关系的运用,由根与系数的关系可以求出,,然后变形为,再整体代入可以求出其值.
【详解】解:∵和是方程的两个解,
∴,,
∴,
∴
,
故选:C.
4.A
【分析】本题考查了列一元二次方程,找准等量关系、正确列出方程是解题的关键.
该款上衣销售量的月平均增长率为,根据3月份销售量和1月份销售量列出一元二次方程求解即可.
【详解】解:该款上衣销售量的月平均增长率为,
由题意可得:,
解得:或不合题意舍弃,
所以该款上衣销售量的月平均增长率为.
故选A.
5.B
【分析】本题考查了一元二次方方程的应用,先求出前行的点数之和,再分别求出该代数式的值分别为、600、465、210时的值,判断即可得解.
【详解】解:由题意可得:前行的点数之和为,
若前行的点数之和为,则,
解得:(舍去)或,即前行的点数之和为,故A不符合题意;
若前行的点数之和为600,则,
解得:,不是整数,即不存在前行的点数之和为600,故B符合题意;
若前行的点数之和为465,则,
解得:或(舍去),即前行的点数之和为465,故C不符合题意;
若前行的点数之和为210,则,
解得:或(舍去),即前行的点数之和为210,故D不符合题意;
故选:B.
6.D
【分析】设较小的数为x,那么较大的数应该为,根据“积为45”可得出:,解方程即可求得这两个数.
【详解】解:设较小的数为x,根据题意得,
解得,.
那么这两个数就应该是5,9或,.
故选:D
【点睛】本题考查了一元二次方程的应用,解题关键是根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
7.C
【详解】试题解析:∵m,n是方程x2﹣2x﹣1=0的两根
∴m2﹣2m=1,n2﹣2n=1
∴7m2﹣14m=7(m2﹣2m)=7,3n2﹣6n=3(n2﹣2n)=3
∵(7m2﹣14m+a)(3n2﹣6n﹣7)=8
∴(7+a)×(﹣4)=8
∴a=﹣9.
故选C.
8.B
【分析】先求解,设运动时间为,可得,,再利用面积建立方程求解即可.
【详解】解:∵,,,
∴,
设运动时间为,
∴,,
∵的面积为,即
,解得:,.
当时,,不成立,舍去,
∴,
故选B.
【点睛】本题考查的是一元二次方程的应用,勾股定理的应用,理解题意,熟练的建立方程求解是解本题的关键.
9.B
【详解】解:∵2x2﹣4x﹣1=0,∴2x2﹣4x=1,∴x2﹣2x=,∴x2﹣2x+1=+1,∴(x﹣1)2=,∴m=﹣1,n=.故选B.
10.B
【分析】此题主要考查了正方形的性质,准确识图,熟练掌握正方形的性质,并根据正方形的面积公式构造方程是解决问题的关键.设正方形B的边长为a,其中,依题意由图①得阴影部分为正方形,且边长为1,则正方形A的边长为,依题意得图②中大正方形的边长为,则,由此解出,进而再求出图②中大正方形的面积即可.
【详解】解:设正方形B的边长为a,其中,
∵将B放在A的内部如图①所示,阴影部分的面积为1,
∴阴影部分为正方形,且边长为1,
∴图①中大正方形的边长为,
即正方形A的边长为,
又∵将A,B无缝隙且无重叠放置后构造新的正方形如图②所示:
∴图②中大正方形的边长为:,
∵图②中阴影部分的面积为7,
∴,
整理得:,
解得:,(不合题意,舍去),
∴图②中大正方形的边长为:
∴图②中大正方形的面积为15.
故选:B.
11.(答案不唯一)
【分析】本题主要考查了一元二次方程的一般形式,熟练掌握一元二次方程的一般形式是解答本题的关键.根据一元二次方程的一般形式写出符合题意的方程即可.
【详解】解:由题意知二次项系数为,且一根为的一元二次方程可以是,
故答案为:(答案不唯一).
12.10或11
【分析】此题考查了解一元二次方程因式分解法,等腰三角形的定义,利用因式分解法求出方程的解得到的值,确定出底与腰,即可求出周长.熟练掌握因式分解法是解本题的关键.
【详解】解:,
,
解得:,,
若3为底,4为腰,三角形三边为3,4,4,周长为;
若3为腰,4为底,三角形三边为3,3,4,周长为.
则这个三角形的周长为10或11,
故答案为:10或11.
13.1
【分析】本题考查了一元二次方程的根与系数的关系和一元二次方程的根的判别式等知识,属于常考题型,熟练掌握一元二次方程的基本知识是解题关键.根据一元二次方程的根与系数的关系可得,解方程即可求出m的值,再代入原方程检验即得答案.
【详解】解:设方程的两个根分别为,,
则,,
根据题意得:,即,
解得或;
当时,原方程为,;
当时,原方程为,,舍去.
∴.
故答案为:1.
14.且
【分析】本题考查了一元二次方程的定义,一元二次方程根的判别式,由题意可得且,解不等式即可求解,掌握以上知识点是解题的关键.
【详解】解:由题意得,且,
解得且,
故答案为:且.
15.19
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
设这群人共有x人,则共摘了个石榴,根据“如果平均分配,每个人可以得到10个石榴”,可列出关于x的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】解:设这群人共有x人,则共摘了个石榴,
根据题意得:,
整理得:,
解得:(不符合题意,舍去),,
∴这群人共有19人.
故答案为:19.
16.
【分析】本题考查根的判别式,根据题意正确找出等量关系列式计算是解决本题的关键.
根据“百位数字使得一元二次方程有实数根”,得到列出关于的不等式,解之得到的取值范围,根据“各位数字之和大于小于得出各位数字之和为或,集合“勤劳数”的定义,分情况讨论可能的数,从而得到对应的“勤劳数”.
【详解】解:根据题意得:,
解得:
∵各位数字之和大于小于,
或,
又∵,
(舍去)或,
若则,该数为,
若则,该数为,
答: 这个“勤劳数” 432或630,
满足条件的所有“勤劳数”的和是,
故答案为:.
17.(1),
(2),
(3)
(4)
【分析】本题考查解一元二次方程,解答此类问题的关键是根据方程的特点,选取合适的方法解方程.
(1)直接利用开方法求解即可;
(2)根据公式法可以解答此方程;
(3)先移项,根据因式分解法可以解答此方程;
(4)先移项,然后根据因式分解法解答此方程.
【详解】(1)解:
或,
解得:,;
(2)解:,
,,,
,
,
,;
(3)解:,
,
,
,
,
解得:;
(4)解:,
,
,
,
解得:.
18.(1)
(2),
【分析】本题考查一元二次方程的解与解一元二次方程,解题的关键是掌握一元二次方程的解,解一元二次方程的方法.
(1)把代入,解出▊,即可;
(2)根据题意,可得方程为,解出方程,即可.
【详解】(1)解:把代入,
∴,
∴“▊”的值为.
(2)解:由题意得,方程为,
∴,
∵,
∴,
∴,.
19.(1)见解析
(2),方程的另一个根为
【分析】本题考查了一元二次方程根的判别式以及根与系数的关系,熟练掌握以上知识点是解题的关键.
(1)根据根的判别式的符号来判定该方程的根的情况;
(2)设方程的另外一个根为,利用根与系数的关系列出关于和的二元一次方程组,解之即可得到答案.
【详解】(1)证明:
无论取何值,原方程总有两个不相等的实数根.
(2)解:设方程的另外一个根为,则
解得:,
故的值为,方程的另一个根为.
20.(1)见解析
(2)
【分析】本题考查了一元二次方程根与系数的关系和根的判别式及勾股定理,解题的关键是掌握相关知识.
(1)根据即可证明无论取什么实数值,该方程总有两个不相等的实数根;
(2)根据勾股定理及根与系数的关系列出关于的方程,解出即可得出答案.
【详解】(1)解:关于的一元二次方程,
,
,
,
无论为何值,,
无论为何值,该方程总有两个不等实根;
(2)解:和恰好是方程的两个根,
,,
是直角三角形,斜边为,
,
,
,
化简得,
解得或,
又时,,不合题意舍去,
.
21.(1)10x,10+x;
(2)每件商品售价为60元时,网店月盈利可达到2000元.
【分析】(1)根据题中已知条件“每件40元的价格购进一批商品,若以单价50元销售,每月可售出200件,调查表明:单价每上涨1元,该商品每月的销售量就减少10件”即可表示;
(2)利用销量×每件的利润=总利润列方程求解即可.
【详解】(1)解:由题意每件商品涨价x元,销量减少10x件,
每件盈利:50-40+x=(10+x)元,
故答案为:10x,10+x;
(2)解:设每件商品涨价x元,网店月盈利可达到2000元,
则,
解得:(舍去)
售价为50+10=60(元),
即每件商品售价为60元时,网店月盈利可达到2000元.
【点睛】本题考查一元二次方程的应用,根据题意找到等量关系列方程是解题的关键.
22.(1)×,×
(2)见解析
【分析】本题考查了因式分解法解一元二次方程.熟练掌握因式分解法解一元二次方程是解题的关键.
(1)根据因式分解法解一元二次方程判断即可;
(2)根据因式分解法解一元二次方程求解即可.
【详解】(1)解:由题意知,小颖×,小明×,
故答案为:×,×;
(2)解:,
,
,
∴或,
解得,,.
23.(1);;;
(2)
(3)b的值为或.
【分析】本题考查根与系数的关系,二次函数图像与性质,不等式性质,二次函数最值情况,解题的关键在于熟练掌握二次函数图像与性质.
(1)根据根与系数的关系得到,以及,即可判断①,利用二次函数的图像与性质得到,进而得到,利用不等式性质变形,即可判断②③.
(2)根据题意得到,结合进行求解,即可解题;
(3)根据题意得到抛物线顶点坐标为,对称轴为;当时,,当时,,由最大值与最小值的差为,分以下三种情况:①当在取得最大值,在取得最小值时,②当在取得最大值,在顶点取得最小值时,③当在取得最大值,在顶点取得最小值时,建立等式求解,即可解题.
【详解】(1)解: 与x轴交点的坐标分别为,,且,
,且抛物线开口向上,
与x轴交点的坐标分别为,,且.
即向上平移1个单位,
,且,
①;
,
,即②;
,即③.
故答案为;;;;
(2)解:,,
,
,
;
(3)解:抛物线顶点坐标为,
对称轴为;
当时,,
当时,,
①当,则,
那么,在取得最大值,在取得最小值时,
有,解得(不符合题意,舍去);
②当,解得,
那么,在取得最大值,在顶点取得最小值时,
有,解得(不符合题意,舍去)或,
③当,解得,
那么,在取得最大值,在顶点取得最小值时,
有,解得(不符合题意,舍去)或;
综上所述,b的值为或.
24.的长为12米
【分析】本题考查了二次函数的应用,根据题意列出函数关系式是解答本类题目的关键.设的长为,则,根据围成的花圃的面积为建立方程求解,排除不符合实际的解,即可得出结果.
【详解】解:设的长为,则,
由已知,,
则
依据题意列方程得:,
解得:(舍),
答:的长为12米.
25.(1)经过或之后,的长为cm;
(2)秒或秒.
【分析】本题考查了一元二次方程的应用,勾股定理,熟练掌握知识点的应用是解题的关键.
()设经过后,则,,,然后由勾股定理列出方程,然后解方程即可;
()设经过秒,由题意得,,,由的面积等于长方形面积的,列出方程,然后解方程即可;
【详解】(1)设经过后,则,,,的长为cm,
根据题意,由勾股定理得:,
即,
解得:,,
答:经过或之后,的长为cm;
(2)设经过秒,的面积等于矩形面积的,
由题意得,,,
∵矩形中,,,
∴,,
∴矩形的面积为:,
∴的面积,
整理得:,
解得,,
答:经过秒或秒,的面积等于长方形面积的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
