第十三章 三角形 专题-- 三角形平分线夹角和求角度问题 专题练 2025-2026学年上期初中数学人教版(2024)八年级上册
文档属性
| 名称 | 第十三章 三角形 专题-- 三角形平分线夹角和求角度问题 专题练 2025-2026学年上期初中数学人教版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 11:59:58 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
三角形 专题-- 三角形平分线夹角和求角度问题 专题练 2025-2026学年上期初中数学人教版(2024)八年级上册
一、单选题
1.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
A.10 ° B.20 °
C.30° D.40°
2.如图,为直角三角形,,为的平分线,与的平分线交于点E,是的外角平分线,与相交于点G,则与的和为( )
A. B. C. D.
3.如图,平分交的平分线于,交的外角平分线于,若,则的度数为( )
A. B. C. D.
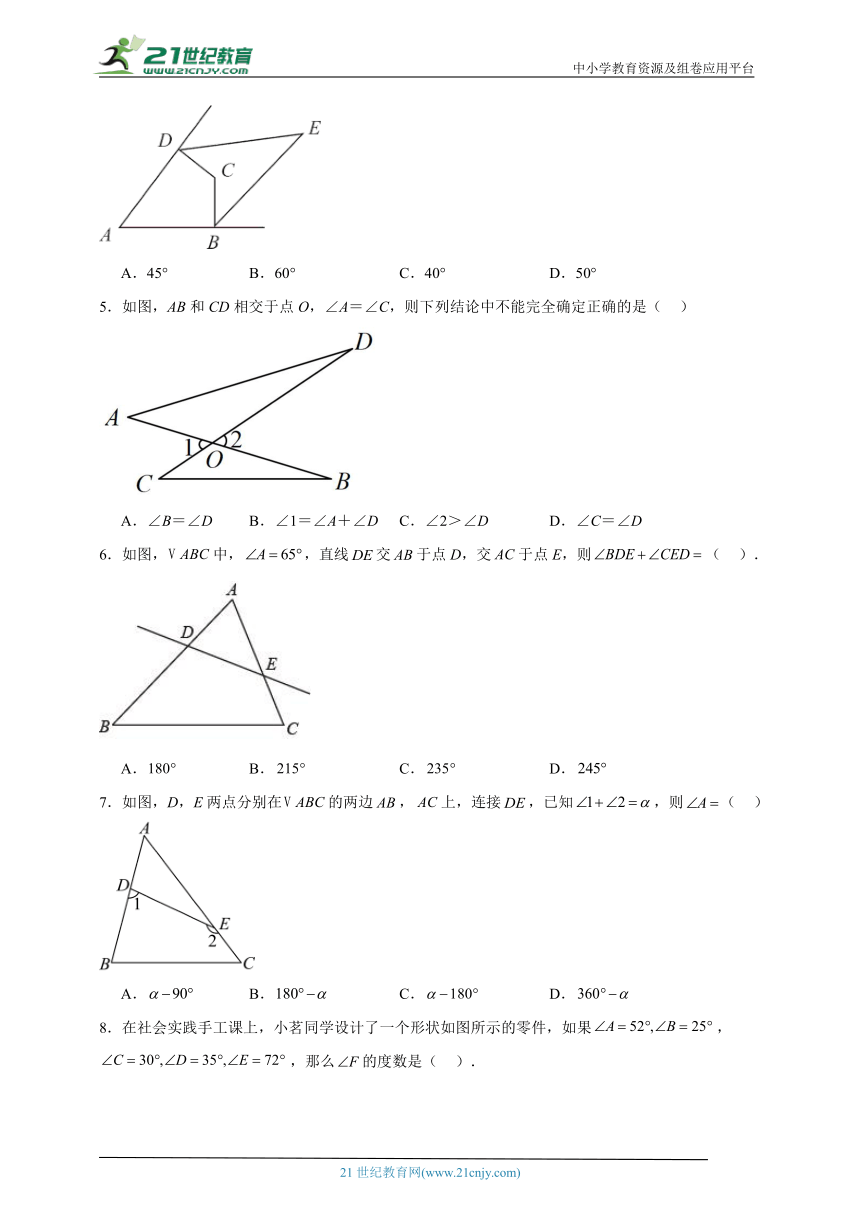
4.如图,四边形中,,与、相邻的两外角平分线交于点E,若,则的度数为( )
A.45° B.60° C.40° D.50°
5.如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
6.如图,中,,直线交于点D,交于点E,则( ).
A. B. C. D.
7.如图,D,E两点分别在的两边,上,连接,已知,则( )
A. B. C. D.
8.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果,,那么的度数是( ).
A. B. C. D.
二、填空题
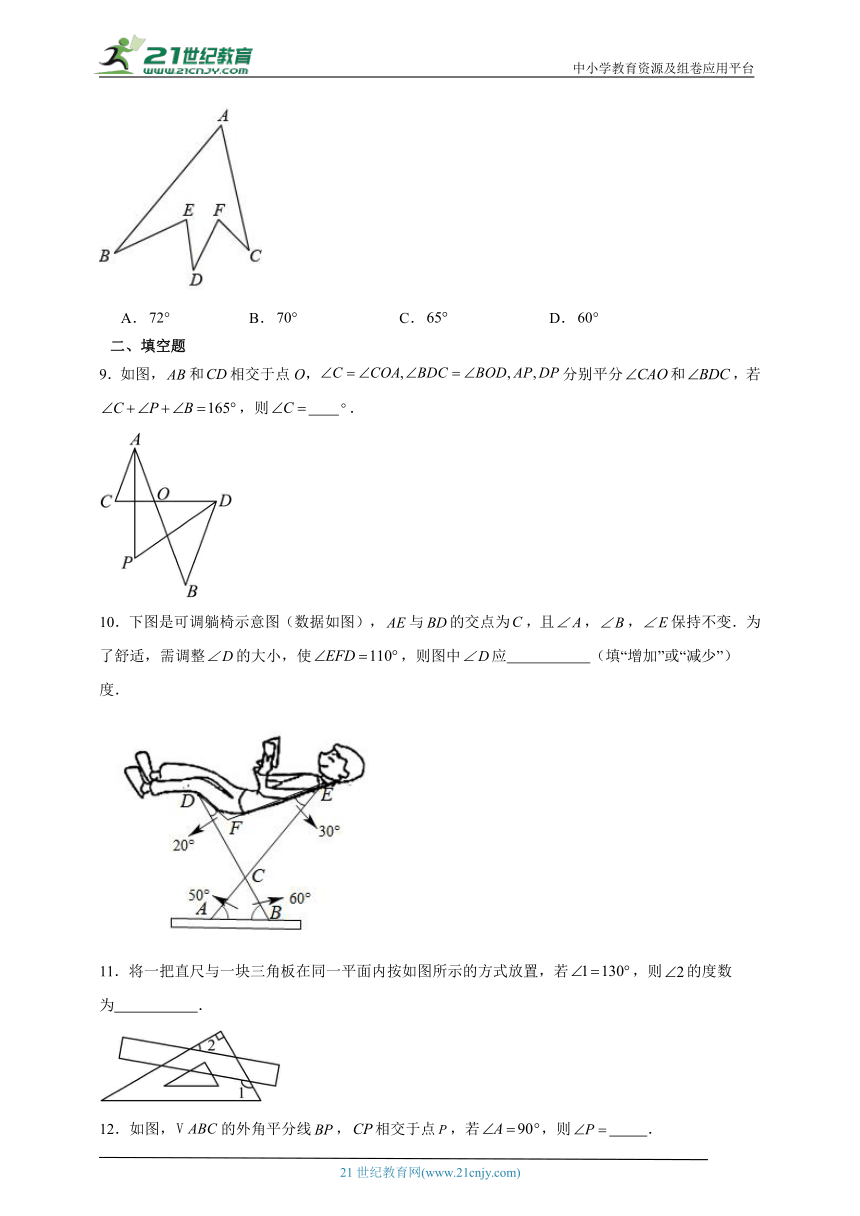
9.如图,和相交于点O,分别平分和,若,则 .
10.下图是可调躺椅示意图(数据如图),与的交点为,且,,保持不变.为了舒适,需调整的大小,使,则图中应 (填“增加”或“减少”) 度.
11.将一把直尺与一块三角板在同一平面内按如图所示的方式放置,若,则的度数为 .
12.如图,的外角平分线,相交于点,若,则 .
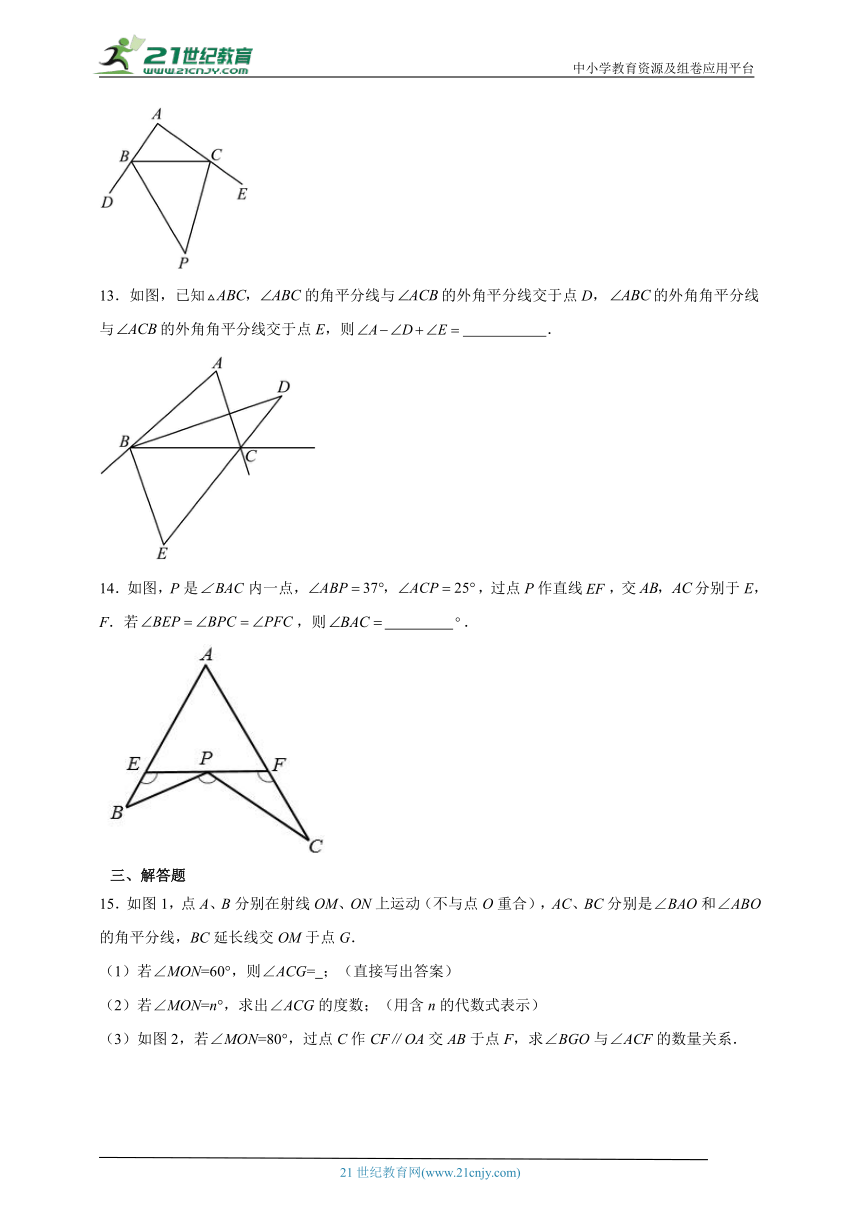
13.如图,已知的角平分线与的外角平分线交于点D,的外角角平分线与的外角角平分线交于点E,则 .
14.如图,P是内一点,,过点P作直线,交分别于E,F.若,则 .
三、解答题
15.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= ;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.
16.如图1,AD、BC交于点O,得到的数学基本图形我们称之为‘8’字形ABCD.
(1)试说明:∠A+∠B=∠C+∠D;
(2)如图2,∠ABC和∠ADC的平分线相交于E,尝试用(1)中的数学基本图形和结论,猜想∠E与∠A、∠C之间的数量关系并说明理由.
17.如图,已知在中,,、分别平分、,相交于点,、分别平分、,相交于点,求、的度数.
18.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
19.如图,在中,分别是的外角平分线,
(1)若,求的度数为 .
(2)若时,求的度数?
20.如图,在锐角三角形中,点,分别在边,上,于点,于点,,求证:.
21.如图,已知于点F ,, 与 互余,求证: .
证明: (已知),
(____________),
(____________),
与 互余(已知),
,
(____________),
(____________),
(____________),
(____________).
22.如图,在四边形中,,.
(1)______度;(用含,的代数式表示)
(2)若,平分与相邻的外角,平分交于点,交于点,判断与的位置关系,并说明理由.
23.如图,在中,直角顶点在直线上,过点、分别作直线的垂线,垂足分别为、求证:.
参考答案
题号 1 2 3 4 5 6 7 8
答案 A D C C D D C B
1.A
【分析】利用四边形内角和是360°可以求得∠DAB+∠ABC=160°.然后由角平分线的性质,邻补角的定义求得∠PAB+∠ABP= ∠DAB+∠ABC+(180 ∠ABC)=90+ (∠DAB+∠ABC)=170,所以根据△ABP的内角和定理求得∠P的度数即可.
【详解】解:如图,
∵∠D+∠C=200 ,∠DAB+∠ABC+∠C+∠D=360,
∴∠DAB+∠ABC=160.
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,
∴∠PAB+∠ABP=∠DAB+∠ABC+(180 ∠ABC)=90+(∠DAB+∠ABC)=170,
∴∠P=180 (∠PAB+∠ABP)=10.
故选:A.
2.D
【分析】利用三角形内角和定理,角平分线的定义求出,,推出,可得结论.
【详解】解:∵,
∴,
∵,分别平分,,
∴,
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,故D正确.
故选:D.
【点睛】本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
3.C
【分析】本题考查角平分线性质、三角形外角的性质、三角形内角和,根据题意得到,推出,根据角平分线性质推出与的和,利用三角形内角和即可解题.
【详解】解:平分,平分,
,,
,
,
,
,
平分,
,
,
.
故选:C.
4.C
【分析】运用四边形的内角和等于,可求的度数,再利用角平分线的性质及三角形的外角性质可求的度数.
【详解】解:如图,连接并延长,
∵,,
∴,
∵、相邻的两外角平分线交于点,
∴,
∵,,
即
∴.
故选:.
【点睛】本题运用四边形的内角和、角平分线的性质及三角形的外角性质,解题关键是准确计算.
5.D
【分析】利用三角形的外角性质,对顶角相等逐一判断即可.
【详解】∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,
∴∠B=∠D,
∵∠1=∠2=∠A+∠D,
∴∠2>∠D,
故选项A,B,C正确,
故选D.
【点睛】本题考查了对顶角的性质,三角形外角的性质,熟练掌握并运用两条性质是解题的关键.
6.D
【分析】
根据三角形内角和定理求出,根据平角的概念计算即可.
【详解】
解:,
,
,
故选:D.
【点睛】本题考查的是三角形内角和定理的应用,掌握三角形内角和等于是解题的关键.
7.C
【分析】本题考查邻补角性质,三角形内角和定理,熟练掌握三角形内角和定理是解题的关键.
先根据邻补角性质求得,再根据三角形内角和定理求解即可.
【详解】解:∵,,
∴,
∵,
∴,
故选:C.
8.B
【分析】延长BE交CF的延长线于O,连接AO,根据三角形内角和定理求出再利用邻补角的性质求出,再根据四边形的内角和求出,根据邻补角的性质即可求出的度数.
【详解】延长BE交CF的延长线于O,连接AO,如图,
∵
∴
同理得
∵
∴
∵
∴
∴
∴,
故选:B.
【点睛】本题考查三角形内角和定理,多边形内角和,三角形的外角的性质,邻补角的性质,解题关键是会添加辅助线,将已知条件联系起来进行求解.三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和;邻补角性质:邻补角互补;多边形内角和:.
9.70
【分析】根据三角形内角和定理可得,设,则,再由分别平分和,可得,,再根据三角形内角和定理可得,从而得到,然后根据得到关于x的方程,即可求解.
【详解】解:如图,
∵,
∴,
∴,
∴,
设,则,
∵分别平分和,
∴,,
∵,,
∴,
∴,
∴,
∵
∴,
解得:,
即.
故答案为:70
【点睛】本题主要考查了三角形内角和定理,一元一次方程的应用,利用参数思想构建方程是解题的关键.
10. 减少 10
【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系,进行计算即可判断.
【详解】解:∵∠A+∠B=50°+60°=110°,
∴∠ACB=180°-110°=70°,
∴∠DCE=70°,
如图,连接CF并延长,
∴∠DFM=∠D+∠DCF=20°+∠DCF,
∠EFM=∠E+∠ECF=30°+∠ECF,
∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,
要使∠EFD=110°,则∠EFD减少了10°,
若只调整∠D的大小,
由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠ D+100°,
因此应将∠D减少10度;
故答案为:①减少;②10.
【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.
11./40度
【分析】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键,根据平行线的性质可得,然后利用三角形外角的性质进行计算即可解答.
【详解】解:如图:
由题意得:,
∴,
∵是的一个外角,
∴,
∵,
∴,
故答案为:.
12.
【分析】本题考查了直角三角形的性质,三角形内角和定理,角平分线的定义,根据直角三角形的性质得到,进而得到,再根据角平分线的定义,三角形内角和定理计算即可,掌握直角三角形的两锐角互余是解题的关键.
【详解】∵,
∴,
∴,
∵,分别为,的平分线,
∴,,
∴,
∴,
故答案为:.
13./90度
【分析】该题主要考查了角形内角和定理,三角形角平分线以及三角形外角的性质,解题的关键是理解题意.
根据角平分线得出,根据三角形外角的性质即可得,再根据内角和定理得出,即可求解.
【详解】解:∵的角平分线与的外角平分线交于点D,的外角角平分线与的外角角平分线交于点E,
∴,
∴,
∴
∴,
∵,,
∴,
∴,
∴
故答案为:.
14.56
【分析】如图,连接,由题意知,,则,由,可知,则,根据,即,计算求解即可.
【详解】解:如图,连接,
由题意知,,
∴,
∵,
∴,,
∵,
∴,
解得,
故答案为:56.
【点睛】本题考查了三角形内角和定理.解题的关键在于明确角度之间的数量关系.
15.(1)60°;(2)90°-n°;(3)∠BGO-∠ACF=50°
【分析】(1)根据三角形内角和定理求出∠BAO+∠ABO,根据角平分线的定义、三角形的外角性质计算,得到答案;
(2)仿照(1)的解法解答;
(3)根据平行线的性质得到∠ACF=∠CAG,根据(2)的结论解答.
【详解】解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°-n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°-n°,
∴∠ACG=∠CBA+∠CAB=90°-n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG,
由(2)得:∠ACG=90°-×80°=50°.
∴∠BGO-∠ACF=50°.
【点睛】本题考查的是角平分线的定义、平行线的性质、三角形的外角性质,掌握两直线平行、内错角相等是解题的关键.
16.(1)见解析;(2)2∠E=∠A+∠C,理由见解析
【分析】(1)利用三角形内角和定理:,结合对顶角相等可得结论.
(2)利用(1)中结论,设∠ABE=∠EBC=x,∠ADE=∠EDC=y,可得∠A+x=∠E+y,∠C+y=∠E+x,两式相加可得结论.
【详解】解:(1)证明:∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)结论:2∠E=∠A+∠C.
理由:∵∠ABC和∠ADC的平分线相交于E,
∴设∠ABE=∠EBC=x,∠ADE=∠EDC=y,
∵∠A+x=∠E+y,∠C+y=∠E+x,
∴∠A+∠C=∠E+∠E,
∴2∠E=∠A+∠C .
【点睛】本题考查的是三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识.
17.;.
【分析】根据三角形内角平分线的交角的基本图形和结论即可得出答案
【详解】解:由三角形内角平分线的交角的基本图形和结论得,;
;
、分别平分、,相交于点,
是的平分线,
.
【点睛】本题考查了三角形的内角和定理,以及三角形的角平分线的性质,熟练掌握相关的知识点是解题的关键.
18..
【分析】根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC,在根据角平分线的性质即可得出
【详解】解:由燕尾角的基本图形与结论可得,
①
②
是的平分线,是的平分线
,.
①-②得,.
【点睛】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.
19.(1)
(2)
【分析】本题考查了与角平分线有关的三角形内角和问题,解题关键是运用三角形的内角和等于180度,以及角平分线平分角的知识结合一起解答,在求角度时,有时不一定需要每个角都求出来,可以利用整体思想.
(1)先由邻补角求得,再根据角平分线以及三角形内角和求得,最后在中再次运用三角形内角和即可求解;
(2)求解方法同(1).
【详解】(1)解:∵,
∴,
∵分别是的外角平分线,
∴,
∴,
∴,
故答案为:;
(2)解:∵,
∴,
∴,
∵分别是的外角平分线,
∴,
∴,
∴.
20.证明见解析
【分析】本题考查了垂直的定义,直角三角形两锐角互余,等角的余角相等,掌握知识点的应用是解题的关键.
由,则,再通过等角的余角相等得出.
【详解】证明:∵,
∴,
∴,
∵,
∴.
21.垂线的定义;直角三角形两个锐角互余;同角的余角相等;已知;两直线平行,内错角相等;等量代换
【分析】本题主要考查了垂线的定义,平行线的性质,同角的余角相等,直角三角形的性质,根据已给推理过程,结合垂线的定义,平行线的性质,同角的余角相等,三角形内角和定理进行证明即可.
【详解】证明: (已知),
(垂线的定义),
(直角三角形两个锐角互余),
与 互余(已知),
,
(同角的余角相等),
(已知),
(两直线平行,内错角相等),
(等量代换).
22.(1);
(2),理由见解析.
【分析】本题主要考查了四边形内角和问题,角平分线的定义,三角形外角的定义以及性质等知识.
(1)由四边形内角和为即可解题.
(2)由平角的定义得出,由(1)可得出,可得出,由角平分线的定义可得出,由三角形外角的定义以及性质可得出,,即可得出,则
【详解】(1)解:∵,,,
∴,
故答案为:.
(2),理由如下:
,
.
.
平分,平分,
,.
.
,
.
.
23.见解析
【分析】本题主要考查了余角的性质,直角三角形两锐角互余:根据,可得,再利用垂直定义可得,从而可得,然后利用同角的余角相等即可求证.
【详解】证明:,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
三角形 专题-- 三角形平分线夹角和求角度问题 专题练 2025-2026学年上期初中数学人教版(2024)八年级上册
一、单选题
1.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
A.10 ° B.20 °
C.30° D.40°
2.如图,为直角三角形,,为的平分线,与的平分线交于点E,是的外角平分线,与相交于点G,则与的和为( )
A. B. C. D.
3.如图,平分交的平分线于,交的外角平分线于,若,则的度数为( )
A. B. C. D.
4.如图,四边形中,,与、相邻的两外角平分线交于点E,若,则的度数为( )
A.45° B.60° C.40° D.50°
5.如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
6.如图,中,,直线交于点D,交于点E,则( ).
A. B. C. D.
7.如图,D,E两点分别在的两边,上,连接,已知,则( )
A. B. C. D.
8.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果,,那么的度数是( ).
A. B. C. D.
二、填空题
9.如图,和相交于点O,分别平分和,若,则 .
10.下图是可调躺椅示意图(数据如图),与的交点为,且,,保持不变.为了舒适,需调整的大小,使,则图中应 (填“增加”或“减少”) 度.
11.将一把直尺与一块三角板在同一平面内按如图所示的方式放置,若,则的度数为 .
12.如图,的外角平分线,相交于点,若,则 .
13.如图,已知的角平分线与的外角平分线交于点D,的外角角平分线与的外角角平分线交于点E,则 .
14.如图,P是内一点,,过点P作直线,交分别于E,F.若,则 .
三、解答题
15.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= ;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.
16.如图1,AD、BC交于点O,得到的数学基本图形我们称之为‘8’字形ABCD.
(1)试说明:∠A+∠B=∠C+∠D;
(2)如图2,∠ABC和∠ADC的平分线相交于E,尝试用(1)中的数学基本图形和结论,猜想∠E与∠A、∠C之间的数量关系并说明理由.
17.如图,已知在中,,、分别平分、,相交于点,、分别平分、,相交于点,求、的度数.
18.如图,是的平分线,CH是的平分线,与CH交于点,若,,求的度数.
19.如图,在中,分别是的外角平分线,
(1)若,求的度数为 .
(2)若时,求的度数?
20.如图,在锐角三角形中,点,分别在边,上,于点,于点,,求证:.
21.如图,已知于点F ,, 与 互余,求证: .
证明: (已知),
(____________),
(____________),
与 互余(已知),
,
(____________),
(____________),
(____________),
(____________).
22.如图,在四边形中,,.
(1)______度;(用含,的代数式表示)
(2)若,平分与相邻的外角,平分交于点,交于点,判断与的位置关系,并说明理由.
23.如图,在中,直角顶点在直线上,过点、分别作直线的垂线,垂足分别为、求证:.
参考答案
题号 1 2 3 4 5 6 7 8
答案 A D C C D D C B
1.A
【分析】利用四边形内角和是360°可以求得∠DAB+∠ABC=160°.然后由角平分线的性质,邻补角的定义求得∠PAB+∠ABP= ∠DAB+∠ABC+(180 ∠ABC)=90+ (∠DAB+∠ABC)=170,所以根据△ABP的内角和定理求得∠P的度数即可.
【详解】解:如图,
∵∠D+∠C=200 ,∠DAB+∠ABC+∠C+∠D=360,
∴∠DAB+∠ABC=160.
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,
∴∠PAB+∠ABP=∠DAB+∠ABC+(180 ∠ABC)=90+(∠DAB+∠ABC)=170,
∴∠P=180 (∠PAB+∠ABP)=10.
故选:A.
2.D
【分析】利用三角形内角和定理,角平分线的定义求出,,推出,可得结论.
【详解】解:∵,
∴,
∵,分别平分,,
∴,
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,故D正确.
故选:D.
【点睛】本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
3.C
【分析】本题考查角平分线性质、三角形外角的性质、三角形内角和,根据题意得到,推出,根据角平分线性质推出与的和,利用三角形内角和即可解题.
【详解】解:平分,平分,
,,
,
,
,
,
平分,
,
,
.
故选:C.
4.C
【分析】运用四边形的内角和等于,可求的度数,再利用角平分线的性质及三角形的外角性质可求的度数.
【详解】解:如图,连接并延长,
∵,,
∴,
∵、相邻的两外角平分线交于点,
∴,
∵,,
即
∴.
故选:.
【点睛】本题运用四边形的内角和、角平分线的性质及三角形的外角性质,解题关键是准确计算.
5.D
【分析】利用三角形的外角性质,对顶角相等逐一判断即可.
【详解】∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,
∴∠B=∠D,
∵∠1=∠2=∠A+∠D,
∴∠2>∠D,
故选项A,B,C正确,
故选D.
【点睛】本题考查了对顶角的性质,三角形外角的性质,熟练掌握并运用两条性质是解题的关键.
6.D
【分析】
根据三角形内角和定理求出,根据平角的概念计算即可.
【详解】
解:,
,
,
故选:D.
【点睛】本题考查的是三角形内角和定理的应用,掌握三角形内角和等于是解题的关键.
7.C
【分析】本题考查邻补角性质,三角形内角和定理,熟练掌握三角形内角和定理是解题的关键.
先根据邻补角性质求得,再根据三角形内角和定理求解即可.
【详解】解:∵,,
∴,
∵,
∴,
故选:C.
8.B
【分析】延长BE交CF的延长线于O,连接AO,根据三角形内角和定理求出再利用邻补角的性质求出,再根据四边形的内角和求出,根据邻补角的性质即可求出的度数.
【详解】延长BE交CF的延长线于O,连接AO,如图,
∵
∴
同理得
∵
∴
∵
∴
∴
∴,
故选:B.
【点睛】本题考查三角形内角和定理,多边形内角和,三角形的外角的性质,邻补角的性质,解题关键是会添加辅助线,将已知条件联系起来进行求解.三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和;邻补角性质:邻补角互补;多边形内角和:.
9.70
【分析】根据三角形内角和定理可得,设,则,再由分别平分和,可得,,再根据三角形内角和定理可得,从而得到,然后根据得到关于x的方程,即可求解.
【详解】解:如图,
∵,
∴,
∴,
∴,
设,则,
∵分别平分和,
∴,,
∵,,
∴,
∴,
∴,
∵
∴,
解得:,
即.
故答案为:70
【点睛】本题主要考查了三角形内角和定理,一元一次方程的应用,利用参数思想构建方程是解题的关键.
10. 减少 10
【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系,进行计算即可判断.
【详解】解:∵∠A+∠B=50°+60°=110°,
∴∠ACB=180°-110°=70°,
∴∠DCE=70°,
如图,连接CF并延长,
∴∠DFM=∠D+∠DCF=20°+∠DCF,
∠EFM=∠E+∠ECF=30°+∠ECF,
∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,
要使∠EFD=110°,则∠EFD减少了10°,
若只调整∠D的大小,
由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠ D+100°,
因此应将∠D减少10度;
故答案为:①减少;②10.
【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.
11./40度
【分析】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键,根据平行线的性质可得,然后利用三角形外角的性质进行计算即可解答.
【详解】解:如图:
由题意得:,
∴,
∵是的一个外角,
∴,
∵,
∴,
故答案为:.
12.
【分析】本题考查了直角三角形的性质,三角形内角和定理,角平分线的定义,根据直角三角形的性质得到,进而得到,再根据角平分线的定义,三角形内角和定理计算即可,掌握直角三角形的两锐角互余是解题的关键.
【详解】∵,
∴,
∴,
∵,分别为,的平分线,
∴,,
∴,
∴,
故答案为:.
13./90度
【分析】该题主要考查了角形内角和定理,三角形角平分线以及三角形外角的性质,解题的关键是理解题意.
根据角平分线得出,根据三角形外角的性质即可得,再根据内角和定理得出,即可求解.
【详解】解:∵的角平分线与的外角平分线交于点D,的外角角平分线与的外角角平分线交于点E,
∴,
∴,
∴
∴,
∵,,
∴,
∴,
∴
故答案为:.
14.56
【分析】如图,连接,由题意知,,则,由,可知,则,根据,即,计算求解即可.
【详解】解:如图,连接,
由题意知,,
∴,
∵,
∴,,
∵,
∴,
解得,
故答案为:56.
【点睛】本题考查了三角形内角和定理.解题的关键在于明确角度之间的数量关系.
15.(1)60°;(2)90°-n°;(3)∠BGO-∠ACF=50°
【分析】(1)根据三角形内角和定理求出∠BAO+∠ABO,根据角平分线的定义、三角形的外角性质计算,得到答案;
(2)仿照(1)的解法解答;
(3)根据平行线的性质得到∠ACF=∠CAG,根据(2)的结论解答.
【详解】解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°-n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°-n°,
∴∠ACG=∠CBA+∠CAB=90°-n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG,
由(2)得:∠ACG=90°-×80°=50°.
∴∠BGO-∠ACF=50°.
【点睛】本题考查的是角平分线的定义、平行线的性质、三角形的外角性质,掌握两直线平行、内错角相等是解题的关键.
16.(1)见解析;(2)2∠E=∠A+∠C,理由见解析
【分析】(1)利用三角形内角和定理:,结合对顶角相等可得结论.
(2)利用(1)中结论,设∠ABE=∠EBC=x,∠ADE=∠EDC=y,可得∠A+x=∠E+y,∠C+y=∠E+x,两式相加可得结论.
【详解】解:(1)证明:∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)结论:2∠E=∠A+∠C.
理由:∵∠ABC和∠ADC的平分线相交于E,
∴设∠ABE=∠EBC=x,∠ADE=∠EDC=y,
∵∠A+x=∠E+y,∠C+y=∠E+x,
∴∠A+∠C=∠E+∠E,
∴2∠E=∠A+∠C .
【点睛】本题考查的是三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识.
17.;.
【分析】根据三角形内角平分线的交角的基本图形和结论即可得出答案
【详解】解:由三角形内角平分线的交角的基本图形和结论得,;
;
、分别平分、,相交于点,
是的平分线,
.
【点睛】本题考查了三角形的内角和定理,以及三角形的角平分线的性质,熟练掌握相关的知识点是解题的关键.
18..
【分析】根据三角形的外角的性质得出燕尾角的基本图形的结论得出∠BDC、∠BOC,在根据角平分线的性质即可得出
【详解】解:由燕尾角的基本图形与结论可得,
①
②
是的平分线,是的平分线
,.
①-②得,.
【点睛】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.
19.(1)
(2)
【分析】本题考查了与角平分线有关的三角形内角和问题,解题关键是运用三角形的内角和等于180度,以及角平分线平分角的知识结合一起解答,在求角度时,有时不一定需要每个角都求出来,可以利用整体思想.
(1)先由邻补角求得,再根据角平分线以及三角形内角和求得,最后在中再次运用三角形内角和即可求解;
(2)求解方法同(1).
【详解】(1)解:∵,
∴,
∵分别是的外角平分线,
∴,
∴,
∴,
故答案为:;
(2)解:∵,
∴,
∴,
∵分别是的外角平分线,
∴,
∴,
∴.
20.证明见解析
【分析】本题考查了垂直的定义,直角三角形两锐角互余,等角的余角相等,掌握知识点的应用是解题的关键.
由,则,再通过等角的余角相等得出.
【详解】证明:∵,
∴,
∴,
∵,
∴.
21.垂线的定义;直角三角形两个锐角互余;同角的余角相等;已知;两直线平行,内错角相等;等量代换
【分析】本题主要考查了垂线的定义,平行线的性质,同角的余角相等,直角三角形的性质,根据已给推理过程,结合垂线的定义,平行线的性质,同角的余角相等,三角形内角和定理进行证明即可.
【详解】证明: (已知),
(垂线的定义),
(直角三角形两个锐角互余),
与 互余(已知),
,
(同角的余角相等),
(已知),
(两直线平行,内错角相等),
(等量代换).
22.(1);
(2),理由见解析.
【分析】本题主要考查了四边形内角和问题,角平分线的定义,三角形外角的定义以及性质等知识.
(1)由四边形内角和为即可解题.
(2)由平角的定义得出,由(1)可得出,可得出,由角平分线的定义可得出,由三角形外角的定义以及性质可得出,,即可得出,则
【详解】(1)解:∵,,,
∴,
故答案为:.
(2),理由如下:
,
.
.
平分,平分,
,.
.
,
.
.
23.见解析
【分析】本题主要考查了余角的性质,直角三角形两锐角互余:根据,可得,再利用垂直定义可得,从而可得,然后利用同角的余角相等即可求证.
【详解】证明:,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
