第1章一元二次方程检测卷(含解析)-数学九年级上册苏科版
文档属性
| 名称 | 第1章一元二次方程检测卷(含解析)-数学九年级上册苏科版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 07:35:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1章一元二次方程检测卷-数学九年级上册苏科版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.若关于x的一元二次方程配方后得到方程,则c的值为( )
A. B.2 C. D.4
3.若是关于x的一元二次方程的一个根,则代数式的值为( )
A. B.1 C. D.2025
4.某公司2025年2月份的利润比1月份的利润增长了,3月份的利润比2月份的利润下降了,则该公司3月份比1月份利润增长了( )
A. B. C. D.
5.定义新运算:,例如:.若关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C. D.
6.已知关于的一元二次方程有两个相等的实数根,则的值是( ).
A. B.或
C.或 D.或
7.定义新运算:对于两个不相等的实数,,我们规定符号表示,中的较大值,如:,等等;按照这个规定,若,则的值是( )
A.5 B.5或 C.5或3 D.3或0
8.4月23日为“世界读书日”,全国国民阅读调查结果发布,2022年和2024年我国成年国民人均纸质图书阅读量分别为4.65本和4.76本,设平均每年阅读量的增长率为,那么可列方程是( )
A.
B.
C.
D.
二、填空题
9.已知关于x方程的一个根为4,则方程的另一个根为 .
10.若关于x的一元二次方程无实数根,则c的取值范围是 .
11.已知关于x的方程若方程的一个根是,则方程的另一个根是 .
12.我国南宋数学家杨辉所著《田亩比类乘除算法》中记载了这样一道题:“直田积八百二十八步,只云阔不及长一十三步,问阔及长各几步”其大意为:一个矩形的面积为828平方步,宽比长少13步,问宽和长各多少步?设矩形的宽为步,根据题意,可列方程为 .
13.将一元二次方程化成(、为常数)的形式,则的值为 .
14.若,是方程的两个实数根,且,则m的值为 .
15.如图,在中,,,,动点P从点C出发,以2的速度沿方向运动;同时动点Q从点B出发,以1的速度沿方向运动.则运动 秒后 P、Q两点相距25.
16.在菱形中,点、分别是、边上的点,将沿翻折在同一平面内,使点的对应点落在上,与的角平分线交于点,点为的中点,连接,若,,,则 .
三、解答题
17.解方程:
(1);
(2).
18.已知,是关于x的一元二次方程的两实数根.
(1)求m的取值范围;
(2)已知等腰的底边,若,恰好是另外两边的边长,求这个三角形的周长.
19.某种商品在某电商平台1月份的销量是5万件,3月份的销量是万件.
(1)若该平台1月份到3月份销量的月平均增长率都相同,求月平均增长率是多少?
(2)某商场销售这种商品,每件进价为40元.市场调研发现:当每件售价为80元时,平均每天能售出20件;而当售价每降低1元时,平均每天就能多售出4件.为尽量减少库存,商场决定降价促销,若想使这种商品的销售利润平均每天达到1400元,每件售价应降低多少元?
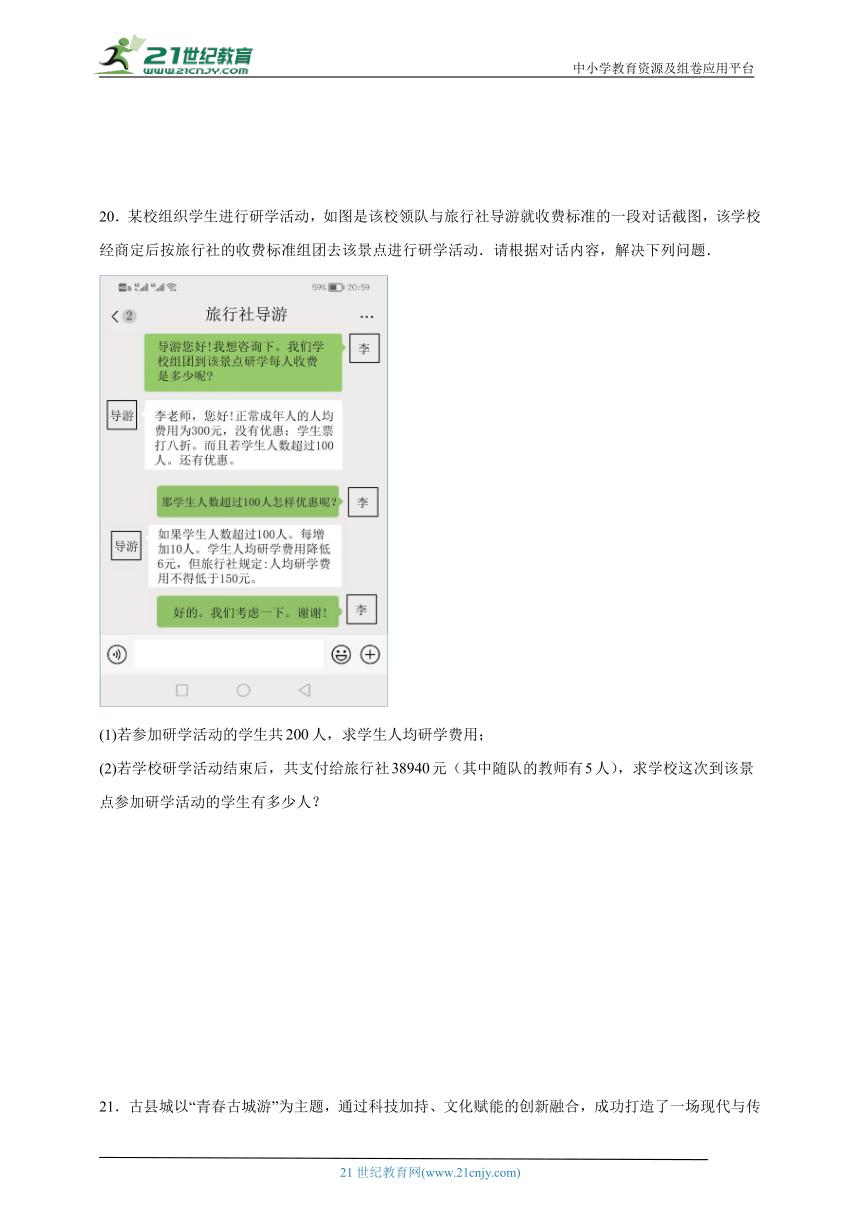
20.某校组织学生进行研学活动,如图是该校领队与旅行社导游就收费标准的一段对话截图,该学校经商定后按旅行社的收费标准组团去该景点进行研学活动.请根据对话内容,解决下列问题.
(1)若参加研学活动的学生共人,求学生人均研学费用;
(2)若学校研学活动结束后,共支付给旅行社元(其中随队的教师有人),求学校这次到该景点参加研学活动的学生有多少人?
21.古县城以“青春古城游”为主题,通过科技加持、文化赋能的创新融合,成功打造了一场现代与传统交织的文旅盛宴.
(1)【科技加持】千架无人机腾空而起,在夜幕绘就“古城星空”,吸引不少游客驻足观看.据统计,假期第一天古县城累计接待游客约5万人次,第三天接待游客达7.2万人次.求游客人数从假期第一天到第三天的日平均增长率.
(2)【文化赋能】烟火气十足的“去古城赶集”汇集非遗手作,地方美食等,重现古城商贸活力.如景区推出古城著名景点冰箱贴:每个冰箱贴的成本为5元,当售价为10元时,平均每天可售出500个;当售价每降低0.5元,平均每天可多售出25个.若要使每天销售冰箱贴获利1800元,则售价应降低多少元?
22.如果关于x的一元二次方程有两个实数根,其中一个实数根是另一个实数根的倍,那么称这样的方程是“倍根方程”.例如一元二次方程的两个根是,,则方程是“倍根方程”.
(1)通过计算,判断是否是“倍根方程”;
(2)若关于的方程是“倍根方程”,求代数式的值;
(3)已知关于的一元二次方程(是常数)是“倍根方程”,请直接写出的值.
《第1章一元二次方程检测卷-数学九年级上册苏科版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D A D C C B B
1.A
【分析】本题考查了一元二次方程的定义,根据一元二次方程的定义(整式方程、一个未知数、未知数最高次数为2)逐一判断选项.
【详解】解:选项A:方程为整式方程,仅含未知数,且的最高次数为2,符合一元二次方程的定义,是一元二次方程;
选项B:方程中含分式,分母含未知数,不是整式方程,不符合一元二次方程的定义,不是一元二次方程;
选项C:方程含两个未知数和,不符合一元二次方程的定义,不是一元二次方程;
选项D:方程化简后为,是一元一次方程,最高次数为1,不符合一元二次方程的定义,不是一元二次方程.
故选:A.
2.D
【分析】本题考查了一元二次方程的配方法,将配方建立等式是解决本题的关键.
将原方程进行配方,比较配方后的常数项,建立等式求解c的值即可.
【详解】解:原方程为,移项得,
配方得:,
因为配方后的方程为,因此有:,
即,解得:.
故选:D.
3.A
【分析】本题考查了一元二次方程的解,熟知相关知识是解题的关键;
将代入方程,利用方程根的定义直接计算代数式的值即可.
【详解】解:∵是方程的根,
∴将代入得:,
移项得:.
故代数式的值为,
故选A.
4.D
【分析】本题考查增长率的实际应用和代数式的运算,解题关键是设1月利润为基础量,通过表示出2月、3月利润,推导3月相对1月的增长关系 .
设1月份利润为1,计算2月份增长后的利润,再计算3月份下降后的利润,最后求3月份相对于1月份的增长率.
【详解】解:设1月份利润为1(单位利润),根据题意得
2月份利润为,
3月份利润为
3月份相对于1月份的增长率为
故选:D.
5.C
【分析】本题主要考查了已知一元二次方程根的情况求参数的取值范围,解题的关键是熟练掌握当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程没有实数根.
先根据题目所给新定义运算法则,得出,再根据“该方程有两个不相等的实数根”得出,列出不等式求解即可.
【详解】解:∵,
∴,即,
∵该方程有两个不相等的实数根,
∴,
解得:.
故选:C.
6.C
【分析】本题考查了一元二次方程根的判别式以及解一元二次方程,掌握,方程有两个不相等的实数根;,方程有两个相等的实数根;,方程没有实数根是解题关键.根据一元二次方程根的判别式,当判别式Δ=0时,方程有两个相等的实数根,计算判别式并解方程即可确定k的值.
【详解】解:关于的一元二次方程有两个相等的实数根,
,
,
或,
解得:或,
故选:C.
7.B
【分析】本题考查了新定义,解一元二次方程 因式分解法.
根据新定义得出求解即可.
【详解】解:∵,,
∴,
即,
∴,
解得.
故选B.
8.B
【分析】本题考查了一元二次方程的应用,根据2022年人均纸质图书阅读量年均增长率年人均纸质图书阅读量列出方程即可.
本题考查平均增长率问题,需根据连续两年的增长率建立方程.
【详解】解:设每年增长率为,可列方程为,
故选:B.
9.
【分析】本题考查根与系数的关系,熟练掌握根与系数的关系,是解题的关键,根据根与系数的关系,得到两根之和为2,进行求解即可.
【详解】解:由题意,可知,方程的两根之和为2,
∵关于x方程的一个根为4,
∴方程的另一个根为;
故答案为:
10.
【分析】本题主要考查了一元二次方程根的判别式.一元二次方程根的判别式.,一元二次方程有两个不相等的实数根;,一元二次方程有两个相等的实数根;,一元二次方程没有实数根.熟练掌握是解决问题的关键.
根据方程无实数根,得,即可得到答案.
【详解】解:∵关于x的一元二次方程无实数根,
∴,
解得.
故答案为:.
11.
【分析】本题考查了解一元二次方程.将已知的方程的根代入方程,求出m的值,然后再解方程求另一个根.
【详解】解:∵方程的一个根是,
∴,
解得:,
方程即为,
解得:,
方程的另一个根是.
故答案为:.
12.
【分析】本题考查了由实际问题抽象出一元二次方程以及数学常识.由矩形的宽及长与宽之间的关系可得出矩形的长为步,再利用矩形的面积公式即可得出关于的一元二次方程,此题得解.
【详解】解:∵矩形的宽为步,且宽比长少13步,
∴矩形的长为步.
依题意,得:.
故答案为:.
13.
【分析】本题考查了利用配方法解一元二次方程,代数式求值,先把移到右边,再方程两边加上,把方程组配成的形式,进而得到的值,最后代入到代数式计算即可求解,掌握配方法是解题的关键.
【详解】解:∵,
∴,
∴,
即,
∴,,
∴,
故答案为:.
14.
【分析】此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合是解题的关键.首先根据根的判别式求得m的取值范围,然后由根与系数的关系来求m的值.
【详解】解:∵,是方程的两个实数根,
∴,
,
解得,
,是方程的两个实数根,
,
又,
,
即,
解得,或,
又,
的值是.
故答案为:
15.10
【分析】本题考查了动点问题、勾股定理及解一元二次方程,根据题意用时间准确表示出,的长并找到等量关系是解题的关键.设运动时间为x秒,则,,根据图形知,根据勾股定理列出方程,解出即可.
【详解】解:设运动x秒后P、Q两点相距25,
则,,
由题意,得,
整理得:,
解得:,不合题意,舍去,
故答案为:
16.
【分析】本题考查了菱形的性质,勾股定理,角直角三角形的性质,解一元二次方程,直角三角形的性质等知识点,难度较大.
连接,过点作交延长线于点,作交于点,过点作于点,可得, ,设,则,则,由翻折得到,设,在中由勾股定理建立方程,解得:(舍),在中,由勾股定理求得,再由勾股定理求解,由勾股定理求解,可得,再由斜边中线得到.
【详解】解:连接,过点作交延长线于点,作交于点,过点作于点,
∵四边形是菱形,
∴,
∴,,
∴在中,,在中,,
设,则,
∴,
∵,
∴,
∵翻折,
∴,设,
∵在中,,
∴,
解得:(舍),
∴,,
∴,
∴在中,,
∵,
∴,
∵,
∴,
解得:,
∵与的角平分线交于点,
∴,
∵,
∴,
∴,
∴
∵点为的中点,
∴,
故答案为:.
17.(1)
(2)
【分析】本题主要考查解一元二次方程,解题的关键是根据方程的特点选择合适的方法求解.
(1)将方程左边因式分解为,再求解.
(2) 利用直接开平方法将原方程转化为两个一元一次方程,再求解即可.
【详解】(1)解:∵,
∴,
则或,
解得;
(2)∵,
∴或,
解得,.
18.(1)且
(2)10
【分析】本题考查了根的判别式、一元二次方程的定义、三角形的三边关系以及等腰三角形的性质;
(1)利用二次项系数非零及根的判别式,可列出关于m的一元一次不等式组,解之可得出m的取值范围;
(2)利用等腰三角形的性质,可得出,进而可得出,解之可得出m的值,将其代入原方程,可求出,的值,再利用三角形的周长公式,即可求出结论.
【详解】(1)解:∵,是关于x的一元二次方程的两实数根,
∴,
解得:且,
∴m的取值范围为且;
(2)解:∵等腰的底边,且,恰好是另外两边的边长,
∴,
∴,
解得:,
∴原方程为,
∴,
∵3,3,4可以组成三角形,
∴这个三角形的周长为.
19.(1)
(2)30元
【分析】本题主要考查了一元二次方程的应用,找准等量关系、正确列出一元二次方程是解题的关键.
(1)设月平均增长率是x,然后根据题意列出关于x的一元二次方程求解即可;
(2)设售价应降低y元,则每件的销售利润为元,每天可售出件,再利用总利润、每件的销售利润和日销售量的关系列出关于y的一元二次方程求解即可.
【详解】(1)解:设月平均增长率是x,
由题意可得:,
解得:,不符合题意,舍去
答:月平均增长率是
(2)解:设售价应降低y元,则每件的销售利润为元,每天可售出件,
由题意可得:,
整理得:,
解得:,,
又要尽量减少库存,
答:每件售价应降低30元.
20.(1)学生人均研学费用为元
(2)学校这次到该景点参加研学活动的学生有人
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)由题意列式计算即可;
(2)设学校这次到该景点参加研学活动的学生有人,根据共支付给旅行社38940元其中随队的领队、教师共人,列出一元二次方程,解之取符合题意的值即可.
【详解】(1)解:由题意可知,(元),
答:学生人均研学费用为元;
(2)解:设学校这次到该景点参加研学活动的学生有人,则学生人均研学活动费用为:
元,
依题意得:,
整理得:,
解得:,,
当时,,符合题意;
当时,,不符合题意,舍去;
答:学校这次到该景点参加研学活动的学生有人.
21.(1)
(2)2元
【分析】本题考查了一元二次方程在增长率问题和销售问题中的应用,根据题意,找到等量关系,正确列出方程是解题的关键.
(1)设日平均增长率为x,根据题意列出一元二次方程求解即可;
(2)设售价降低a元,根据题意列出一元二次方程求解即可.
【详解】(1)解:设日平均增长率为x,
解得 ,(舍)
答:日平均增长率为.
(2)解:设售价降低a元,
,
解得 ,(负值不合题意,舍去)
答:售价应降低2元.
22.(1)是“倍根方程”,理由见解析;
(2)当时,;当时,;
(3)的值为或.
【分析】本题主要考查了根与系数的关系,解一元二次方程,代数式求值,掌握知识点的应用是解题的关键.
()利用因式分解法解方程得,,然后根据“倍根方程”定义即可;
()由得,,根据“倍根方程”定义可得或,然后代入求解即可;
()由关于的一元二次方程(是常数)是“倍根方程”,设较小的根为,较大的为,根据根与系数的关系得,然后解方程即可.
【详解】(1)解:是“倍根方程”,理由,
∴,,
∴,
∴是“倍根方程”;
(2)解:由得,,
∵关于的方程是“倍根方程”,
∴或,
∴或,
当时,;
当时,;
(3)解:∵关于的一元二次方程(是常数)是“倍根方程”,
∴设较小的根为,较大的为,
∴,
解得:或,
∴的值为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1章一元二次方程检测卷-数学九年级上册苏科版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.若关于x的一元二次方程配方后得到方程,则c的值为( )
A. B.2 C. D.4
3.若是关于x的一元二次方程的一个根,则代数式的值为( )
A. B.1 C. D.2025
4.某公司2025年2月份的利润比1月份的利润增长了,3月份的利润比2月份的利润下降了,则该公司3月份比1月份利润增长了( )
A. B. C. D.
5.定义新运算:,例如:.若关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C. D.
6.已知关于的一元二次方程有两个相等的实数根,则的值是( ).
A. B.或
C.或 D.或
7.定义新运算:对于两个不相等的实数,,我们规定符号表示,中的较大值,如:,等等;按照这个规定,若,则的值是( )
A.5 B.5或 C.5或3 D.3或0
8.4月23日为“世界读书日”,全国国民阅读调查结果发布,2022年和2024年我国成年国民人均纸质图书阅读量分别为4.65本和4.76本,设平均每年阅读量的增长率为,那么可列方程是( )
A.
B.
C.
D.
二、填空题
9.已知关于x方程的一个根为4,则方程的另一个根为 .
10.若关于x的一元二次方程无实数根,则c的取值范围是 .
11.已知关于x的方程若方程的一个根是,则方程的另一个根是 .
12.我国南宋数学家杨辉所著《田亩比类乘除算法》中记载了这样一道题:“直田积八百二十八步,只云阔不及长一十三步,问阔及长各几步”其大意为:一个矩形的面积为828平方步,宽比长少13步,问宽和长各多少步?设矩形的宽为步,根据题意,可列方程为 .
13.将一元二次方程化成(、为常数)的形式,则的值为 .
14.若,是方程的两个实数根,且,则m的值为 .
15.如图,在中,,,,动点P从点C出发,以2的速度沿方向运动;同时动点Q从点B出发,以1的速度沿方向运动.则运动 秒后 P、Q两点相距25.
16.在菱形中,点、分别是、边上的点,将沿翻折在同一平面内,使点的对应点落在上,与的角平分线交于点,点为的中点,连接,若,,,则 .
三、解答题
17.解方程:
(1);
(2).
18.已知,是关于x的一元二次方程的两实数根.
(1)求m的取值范围;
(2)已知等腰的底边,若,恰好是另外两边的边长,求这个三角形的周长.
19.某种商品在某电商平台1月份的销量是5万件,3月份的销量是万件.
(1)若该平台1月份到3月份销量的月平均增长率都相同,求月平均增长率是多少?
(2)某商场销售这种商品,每件进价为40元.市场调研发现:当每件售价为80元时,平均每天能售出20件;而当售价每降低1元时,平均每天就能多售出4件.为尽量减少库存,商场决定降价促销,若想使这种商品的销售利润平均每天达到1400元,每件售价应降低多少元?
20.某校组织学生进行研学活动,如图是该校领队与旅行社导游就收费标准的一段对话截图,该学校经商定后按旅行社的收费标准组团去该景点进行研学活动.请根据对话内容,解决下列问题.
(1)若参加研学活动的学生共人,求学生人均研学费用;
(2)若学校研学活动结束后,共支付给旅行社元(其中随队的教师有人),求学校这次到该景点参加研学活动的学生有多少人?
21.古县城以“青春古城游”为主题,通过科技加持、文化赋能的创新融合,成功打造了一场现代与传统交织的文旅盛宴.
(1)【科技加持】千架无人机腾空而起,在夜幕绘就“古城星空”,吸引不少游客驻足观看.据统计,假期第一天古县城累计接待游客约5万人次,第三天接待游客达7.2万人次.求游客人数从假期第一天到第三天的日平均增长率.
(2)【文化赋能】烟火气十足的“去古城赶集”汇集非遗手作,地方美食等,重现古城商贸活力.如景区推出古城著名景点冰箱贴:每个冰箱贴的成本为5元,当售价为10元时,平均每天可售出500个;当售价每降低0.5元,平均每天可多售出25个.若要使每天销售冰箱贴获利1800元,则售价应降低多少元?
22.如果关于x的一元二次方程有两个实数根,其中一个实数根是另一个实数根的倍,那么称这样的方程是“倍根方程”.例如一元二次方程的两个根是,,则方程是“倍根方程”.
(1)通过计算,判断是否是“倍根方程”;
(2)若关于的方程是“倍根方程”,求代数式的值;
(3)已知关于的一元二次方程(是常数)是“倍根方程”,请直接写出的值.
《第1章一元二次方程检测卷-数学九年级上册苏科版》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D A D C C B B
1.A
【分析】本题考查了一元二次方程的定义,根据一元二次方程的定义(整式方程、一个未知数、未知数最高次数为2)逐一判断选项.
【详解】解:选项A:方程为整式方程,仅含未知数,且的最高次数为2,符合一元二次方程的定义,是一元二次方程;
选项B:方程中含分式,分母含未知数,不是整式方程,不符合一元二次方程的定义,不是一元二次方程;
选项C:方程含两个未知数和,不符合一元二次方程的定义,不是一元二次方程;
选项D:方程化简后为,是一元一次方程,最高次数为1,不符合一元二次方程的定义,不是一元二次方程.
故选:A.
2.D
【分析】本题考查了一元二次方程的配方法,将配方建立等式是解决本题的关键.
将原方程进行配方,比较配方后的常数项,建立等式求解c的值即可.
【详解】解:原方程为,移项得,
配方得:,
因为配方后的方程为,因此有:,
即,解得:.
故选:D.
3.A
【分析】本题考查了一元二次方程的解,熟知相关知识是解题的关键;
将代入方程,利用方程根的定义直接计算代数式的值即可.
【详解】解:∵是方程的根,
∴将代入得:,
移项得:.
故代数式的值为,
故选A.
4.D
【分析】本题考查增长率的实际应用和代数式的运算,解题关键是设1月利润为基础量,通过表示出2月、3月利润,推导3月相对1月的增长关系 .
设1月份利润为1,计算2月份增长后的利润,再计算3月份下降后的利润,最后求3月份相对于1月份的增长率.
【详解】解:设1月份利润为1(单位利润),根据题意得
2月份利润为,
3月份利润为
3月份相对于1月份的增长率为
故选:D.
5.C
【分析】本题主要考查了已知一元二次方程根的情况求参数的取值范围,解题的关键是熟练掌握当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程没有实数根.
先根据题目所给新定义运算法则,得出,再根据“该方程有两个不相等的实数根”得出,列出不等式求解即可.
【详解】解:∵,
∴,即,
∵该方程有两个不相等的实数根,
∴,
解得:.
故选:C.
6.C
【分析】本题考查了一元二次方程根的判别式以及解一元二次方程,掌握,方程有两个不相等的实数根;,方程有两个相等的实数根;,方程没有实数根是解题关键.根据一元二次方程根的判别式,当判别式Δ=0时,方程有两个相等的实数根,计算判别式并解方程即可确定k的值.
【详解】解:关于的一元二次方程有两个相等的实数根,
,
,
或,
解得:或,
故选:C.
7.B
【分析】本题考查了新定义,解一元二次方程 因式分解法.
根据新定义得出求解即可.
【详解】解:∵,,
∴,
即,
∴,
解得.
故选B.
8.B
【分析】本题考查了一元二次方程的应用,根据2022年人均纸质图书阅读量年均增长率年人均纸质图书阅读量列出方程即可.
本题考查平均增长率问题,需根据连续两年的增长率建立方程.
【详解】解:设每年增长率为,可列方程为,
故选:B.
9.
【分析】本题考查根与系数的关系,熟练掌握根与系数的关系,是解题的关键,根据根与系数的关系,得到两根之和为2,进行求解即可.
【详解】解:由题意,可知,方程的两根之和为2,
∵关于x方程的一个根为4,
∴方程的另一个根为;
故答案为:
10.
【分析】本题主要考查了一元二次方程根的判别式.一元二次方程根的判别式.,一元二次方程有两个不相等的实数根;,一元二次方程有两个相等的实数根;,一元二次方程没有实数根.熟练掌握是解决问题的关键.
根据方程无实数根,得,即可得到答案.
【详解】解:∵关于x的一元二次方程无实数根,
∴,
解得.
故答案为:.
11.
【分析】本题考查了解一元二次方程.将已知的方程的根代入方程,求出m的值,然后再解方程求另一个根.
【详解】解:∵方程的一个根是,
∴,
解得:,
方程即为,
解得:,
方程的另一个根是.
故答案为:.
12.
【分析】本题考查了由实际问题抽象出一元二次方程以及数学常识.由矩形的宽及长与宽之间的关系可得出矩形的长为步,再利用矩形的面积公式即可得出关于的一元二次方程,此题得解.
【详解】解:∵矩形的宽为步,且宽比长少13步,
∴矩形的长为步.
依题意,得:.
故答案为:.
13.
【分析】本题考查了利用配方法解一元二次方程,代数式求值,先把移到右边,再方程两边加上,把方程组配成的形式,进而得到的值,最后代入到代数式计算即可求解,掌握配方法是解题的关键.
【详解】解:∵,
∴,
∴,
即,
∴,,
∴,
故答案为:.
14.
【分析】此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合是解题的关键.首先根据根的判别式求得m的取值范围,然后由根与系数的关系来求m的值.
【详解】解:∵,是方程的两个实数根,
∴,
,
解得,
,是方程的两个实数根,
,
又,
,
即,
解得,或,
又,
的值是.
故答案为:
15.10
【分析】本题考查了动点问题、勾股定理及解一元二次方程,根据题意用时间准确表示出,的长并找到等量关系是解题的关键.设运动时间为x秒,则,,根据图形知,根据勾股定理列出方程,解出即可.
【详解】解:设运动x秒后P、Q两点相距25,
则,,
由题意,得,
整理得:,
解得:,不合题意,舍去,
故答案为:
16.
【分析】本题考查了菱形的性质,勾股定理,角直角三角形的性质,解一元二次方程,直角三角形的性质等知识点,难度较大.
连接,过点作交延长线于点,作交于点,过点作于点,可得, ,设,则,则,由翻折得到,设,在中由勾股定理建立方程,解得:(舍),在中,由勾股定理求得,再由勾股定理求解,由勾股定理求解,可得,再由斜边中线得到.
【详解】解:连接,过点作交延长线于点,作交于点,过点作于点,
∵四边形是菱形,
∴,
∴,,
∴在中,,在中,,
设,则,
∴,
∵,
∴,
∵翻折,
∴,设,
∵在中,,
∴,
解得:(舍),
∴,,
∴,
∴在中,,
∵,
∴,
∵,
∴,
解得:,
∵与的角平分线交于点,
∴,
∵,
∴,
∴,
∴
∵点为的中点,
∴,
故答案为:.
17.(1)
(2)
【分析】本题主要考查解一元二次方程,解题的关键是根据方程的特点选择合适的方法求解.
(1)将方程左边因式分解为,再求解.
(2) 利用直接开平方法将原方程转化为两个一元一次方程,再求解即可.
【详解】(1)解:∵,
∴,
则或,
解得;
(2)∵,
∴或,
解得,.
18.(1)且
(2)10
【分析】本题考查了根的判别式、一元二次方程的定义、三角形的三边关系以及等腰三角形的性质;
(1)利用二次项系数非零及根的判别式,可列出关于m的一元一次不等式组,解之可得出m的取值范围;
(2)利用等腰三角形的性质,可得出,进而可得出,解之可得出m的值,将其代入原方程,可求出,的值,再利用三角形的周长公式,即可求出结论.
【详解】(1)解:∵,是关于x的一元二次方程的两实数根,
∴,
解得:且,
∴m的取值范围为且;
(2)解:∵等腰的底边,且,恰好是另外两边的边长,
∴,
∴,
解得:,
∴原方程为,
∴,
∵3,3,4可以组成三角形,
∴这个三角形的周长为.
19.(1)
(2)30元
【分析】本题主要考查了一元二次方程的应用,找准等量关系、正确列出一元二次方程是解题的关键.
(1)设月平均增长率是x,然后根据题意列出关于x的一元二次方程求解即可;
(2)设售价应降低y元,则每件的销售利润为元,每天可售出件,再利用总利润、每件的销售利润和日销售量的关系列出关于y的一元二次方程求解即可.
【详解】(1)解:设月平均增长率是x,
由题意可得:,
解得:,不符合题意,舍去
答:月平均增长率是
(2)解:设售价应降低y元,则每件的销售利润为元,每天可售出件,
由题意可得:,
整理得:,
解得:,,
又要尽量减少库存,
答:每件售价应降低30元.
20.(1)学生人均研学费用为元
(2)学校这次到该景点参加研学活动的学生有人
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)由题意列式计算即可;
(2)设学校这次到该景点参加研学活动的学生有人,根据共支付给旅行社38940元其中随队的领队、教师共人,列出一元二次方程,解之取符合题意的值即可.
【详解】(1)解:由题意可知,(元),
答:学生人均研学费用为元;
(2)解:设学校这次到该景点参加研学活动的学生有人,则学生人均研学活动费用为:
元,
依题意得:,
整理得:,
解得:,,
当时,,符合题意;
当时,,不符合题意,舍去;
答:学校这次到该景点参加研学活动的学生有人.
21.(1)
(2)2元
【分析】本题考查了一元二次方程在增长率问题和销售问题中的应用,根据题意,找到等量关系,正确列出方程是解题的关键.
(1)设日平均增长率为x,根据题意列出一元二次方程求解即可;
(2)设售价降低a元,根据题意列出一元二次方程求解即可.
【详解】(1)解:设日平均增长率为x,
解得 ,(舍)
答:日平均增长率为.
(2)解:设售价降低a元,
,
解得 ,(负值不合题意,舍去)
答:售价应降低2元.
22.(1)是“倍根方程”,理由见解析;
(2)当时,;当时,;
(3)的值为或.
【分析】本题主要考查了根与系数的关系,解一元二次方程,代数式求值,掌握知识点的应用是解题的关键.
()利用因式分解法解方程得,,然后根据“倍根方程”定义即可;
()由得,,根据“倍根方程”定义可得或,然后代入求解即可;
()由关于的一元二次方程(是常数)是“倍根方程”,设较小的根为,较大的为,根据根与系数的关系得,然后解方程即可.
【详解】(1)解:是“倍根方程”,理由,
∴,,
∴,
∴是“倍根方程”;
(2)解:由得,,
∵关于的方程是“倍根方程”,
∴或,
∴或,
当时,;
当时,;
(3)解:∵关于的一元二次方程(是常数)是“倍根方程”,
∴设较小的根为,较大的为,
∴,
解得:或,
∴的值为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
