第五章 统计与概率 增分测评卷
文档属性
| 名称 | 第五章 统计与概率 增分测评卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 356.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2026-02-06 00:00:00 | ||
图片预览



文档简介
(
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第五章 统计与概率
全卷满分150分 考试用时120分钟
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.古代科举制度始于隋而成于唐,完备于宋,明代则是其发展的鼎盛阶段,其中表现之一为会试分南卷、北卷、中卷,并按比例录取,录取比例为11∶7∶2.若明宣德五年会试录取人数为100,则中卷录取人数为( )
A.10 B.15
C.30 D.35
2.某课外小组为了了解什么样的方式最能增强同学们进行垃圾分类的意识,随机对该校同学进行问卷调查,根据调查结果,得到如图所示的统计图,已知每个回答该问卷的同学都只能在问卷的五个选项中选择一个,则以下结论中错误的是( )
A.回答该问卷的总人数不可能是100
B.回答该问卷的同学中,选择“设置分类明确的垃圾桶”的人数最多
C.回答该问卷的同学中,选择“学校团委会宣传”的人数最少
D.回答该问卷的同学中,选择“播放公益广告”的比选择“学校要求”的少8人
3.抛掷一枚质地均匀的正方体骰子,观察向上一面的点数,则下列是互斥事件但不是对立事件的是( )
A.“大于3点”与“不大于3点” B.“大于3点”与“小于2点”
C.“大于3点”与“小于4点” D.“大于3点”与“小于5点”
4.为了加强对学生的营养健康监测,某校在3 000名学生中,抽查了100名学生的体重数据情况.根据所得数据绘制样本的频率分布直方图如图所示(同一组的数据用该组区间的中点值作代表),则下列结论不正确的是( )
A.样本数据的众数为65
B.该校学生中体重低于65 kg的学生大约为1 200人
C.样本数据的80%分位数为72.5
D.样本数据的平均值为66.75
5.一个袋中装有四个形状、大小完全相同的球,球的编号分别为1,2,3,4.先从袋中随机取一个球,记该球的编号为m,将球放回袋中,再从袋中随机取一个球,记该球的编号为n,则m≥n+1的概率为( )
A.
6.排球比赛的规则是5局3胜制(无平局),在某次排球比赛中,甲队在每局比赛中获胜的概率都相等,均为,前2局中乙队以2∶0领先,则最后乙队获胜的概率是( )
A.
7.已知x1,x2,…,xn的平均数为,y1,y2,…,ym的平均数为,且,若x1,x2,…,xn,y1,y2,…,ym的平均数,其中0A.nm C.n=m D.不能确定
8.根据气象学上的标准,连续5天的日平均气温低于10 ℃即为入冬,某地将连续5天的日平均气温的记录数据(记录数据都是自然数)作为一组样本,现有4组样本①②③④,它们各自的数据特征如下:①平均数<4;②平均数<4且极差小于或等于3;③平均数<4且标准差s≤4;④众数等于5且极差小于或等于4.
则4组样本中一定符合入冬标准的有( )
A.1组 B.2组 C.3组 D.4组
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品,若用C表示抽到次品这一事件,则下列说法不正确的是( )
A.事件C发生的概率为 B.事件C发生的频率为
C.事件C发生的概率接近 D.每抽10台电视机,必有1台次品
10.下图为2022年2月至2023年2月建筑业和服务业的商务活动指数,该指数等于50%反映该行业经济与上月比较无变化,大于50%反映该行业经济比上月总体上升,小于50%反映该行业经济比上月总体下降,则下列说法正确的是( )
A.2022年9月至12月服务业经济持续下降
B.2022年9月至12月建筑业经济持续下降
C.2022年5月建筑业经济上升幅度最小
D.2023年2月服务业经济上升幅度最大
11.算盘是我国古代一项伟大的发明,是一类重要的计算工具.现有一把初始状态的算盘如图所示,自右向左,分别表示个位、十位、百位、千位等,上面一粒珠子(简称上珠)代表5,下面一粒珠子(简称下珠)代表1,五粒下珠表示的数的大小等于同组一粒上珠表示的数的大小.例如,个位拨动一粒上珠、十位拨动一粒下珠至梁上,表示数字15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,设事件A=“表示的四位数能被3整除”,B=“表示的四位数能被5整除”,则( )
A.P(A)=
C.P(A∪B)=
三、填空题(本题共3小题,每小题5分,共15分)
12.已知三个事件A,B,C两两互斥,且P(A)=0.3,P()=0.6,P(C)=0.2,则P(A∪B∪C)= .
13.如图所示的茎叶图记录了甲、乙两支篮球队各6名队员某场比赛的得分数据(单位:分).若这两组数据的中位数相等,且平均值也相等,则x+y= .
14.甲、乙两个袋子中分别装有若干个大小和质地均相同的红球和绿球,甲、乙两个袋子中的球的个数之比为1∶3,已知从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率为p.若从甲袋中有放回地摸球,每次摸出一个,直至第2次摸到红球即停止,则恰好摸4次停止的概率为 ;若将甲、乙两个袋子中的球装在一起后,从中摸出一个红球的概率是,则p的值为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
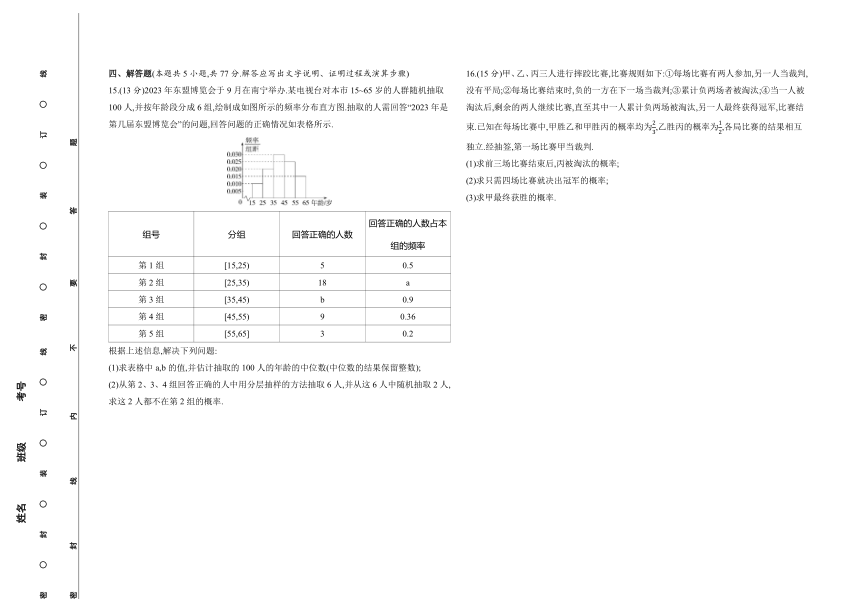
15.(13分)2023年东盟博览会于9月在南宁举办.某电视台对本市15~65岁的人群随机抽取100人,并按年龄段分成6组,绘制成如图所示的频率分布直方图.抽取的人需回答“2023年是第几届东盟博览会”的问题,回答问题的正确情况如表格所示.
组号 分组 回答正确的人数 回答正确的人数占本组的频率
第1组 [15,25) 5 0.5
第2组 [25,35) 18 a
第3组 [35,45) b 0.9
第4组 [45,55) 9 0.36
第5组 [55,65] 3 0.2
根据上述信息,解决下列问题:
(1)求表格中a,b的值,并估计抽取的100人的年龄的中位数(中位数的结果保留整数);
(2)从第2、3、4组回答正确的人中用分层抽样的方法抽取6人,并从这6人中随机抽取2人,求这2人都不在第2组的概率.
16.(15分)甲、乙、丙三人进行摔跤比赛,比赛规则如下:①每场比赛有两人参加,另一人当裁判,没有平局;②每场比赛结束时,负的一方在下一场当裁判;③累计负两场者被淘汰;④当一人被淘汰后,剩余的两人继续比赛,直至其中一人累计负两场被淘汰,另一人最终获得冠军,比赛结束.已知在每场比赛中,甲胜乙和甲胜丙的概率均为,乙胜丙的概率为,各局比赛的结果相互独立.经抽签,第一场比赛甲当裁判.
(1)求前三场比赛结束后,丙被淘汰的概率;
(2)求只需四场比赛就决出冠军的概率;
(3)求甲最终获胜的概率.
17.(15分)有一家经销鲜花产品的微店,为保障售出的百合花的品质,每天从云南鲜花基地空运固定数量的百合花,若有剩余,则免费分赠给第二天购花的顾客,若不足,则从本地鲜花供应商处进货.某年四月前10天,微店百合花的售价为每枝2元,从云南空运来的百合花每枝进价为1.6元,本地供应商处的百合花每枝进价为1.8元.微店这10天的订单中百合花的日需求量(单位:枝)依次为251,255,231,243,263,241,265,255,244,252.
(1)求该年四月前10天订单中百合花日需求量的平均数和众数,并完成频率分布直方图;
(2)预计该年四月的后20天的订单中,百合花日需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(1)中频率分布直方图判断微店每天从云南鲜花基地固定空运250枝,还是255枝百合花,四月后20天百合花的销售总利润更大(同一组中的需求量数据用该组区间的中点值作代表,各区间的概率用该区间的频率代替).
18.(17分)某企业生产两种电路子模块R,Q,如图所示.要求在每个模块中,不同位置接入不同类型的电子元件,且备选电子元件为A,B,C型.假设不同位置的元件是否正常工作不受其他元件影响.在电路子模块R中,当1号位与2号位元件中至少有一个正常工作时,电路子模块才能正常工作;在电路子模块Q中,当1号位元件正常工作,且2号位与3号位元件中至少有一个正常工作时,电路子模块才能正常工作.
(1)若A,B型备选电子元件正常工作的概率分别为0.9,0.8,依次接入位置1,2,求此时电路子模块R能正常工作的概率;
(2)若A,B,C型备选电子元件正常工作的概率分别为0.7,0.8,0.9,如何接入备选电子元件,电路子模块Q能正常工作的概率最大 并说明理由.
19.(17分)某玻璃工艺品加工厂有2条生产线用于生产某款产品,每条生产线一天能生产200件该产品,该产品市场评级规定:评分在10分及以上的为A等品,低于10分的为B等品.厂家将A等品售价定为2 000元/件,B等品售价定为1 200元/件.下面是检验员在现有生产线上随机抽取的16件产品的评分(单位:分):
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得≈0.045,其中xi为抽取的第i件产品的评分(单位:分),i=1,2,…,16.
该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费1 500万元,改进后该条生产线产能不变,但生产出的每件产品的评分均提高0.05分,已知该厂现有1 500万元的资金.
(1)若厂家用这1 500万元改进一条生产线,根据随机抽取的16件产品的评分,估计:
①改进后该生产线生产的产品中A等品所占的比例;
②改进后该厂生产的所有产品评分的平均数和方差;
(2)某金融机构向该厂推销一款年收益率为8.2%的理财产品,请你利用所学知识分析,将这1 500万元用于购买该款理财产品所获得的收益与用于改进一条生产线使产品评分提高所增加的收益相比,一年后哪种方案的收益更大.(一年按365天计算)
答案与解析
第五章 统计与概率
1.A 2.D 3.B 4.A 5.C 6.B
7.A 8.B 9.ACD 10.ACD 11.ACD
1.A 依题意知,中卷录取人数为100×=10.
2.D 根据题意,当回答该问卷的总人数为100时,选择③④的同学人数不是整数,所以总人数不可能是100,故A中结论正确;
从题中统计图可得回答该问卷的同学中,选择⑤的人数最多,选择③的人数最少,故B、C中结论正确;
回答该问卷的同学中,选择“播放公益广告”的人数比选择“学校要求”的人数少8%,故D中结论错误.
3.B 对于A,事件“大于3点”指“点数为4或5或6”,事件“不大于3点”指“点数为1或2或3”,
所以事件“大于3点”与“不大于3点”不可能同时发生,且两事件的和事件为必然事件,所以事件“大于3点”与事件“不大于3点”是互斥事件,且是对立事件,A错误;
对于B,事件“小于2点”指“点数为1”,所以事件“大于3点”与“小于2点”不可能同时发生,但它们的和事件不是必然事件,所以事件“大于3点”与事件“小于2点”为互斥事件,但不是对立事件,B正确;
对于C,事件“小于4点”指“点数为1或2或3”,
所以事件“大于3点”与“小于4点”不可能同时发生,且两事件的和事件为必然事件,所以事件“大于3点”与事件“小于4点”是互斥事件,且是对立事件,C错误;
对于D,事件“小于5点”指“点数为1或2或3或4”,
所以事件“大于3点”与“小于5点”可能同时发生,
所以事件“大于3点”与事件“小于5点”不是互斥事件,D错误.故选B.
4.A 对于A,样本数据的众数为67.5,故A中结论错误;
对于B,该校学生中低于65 kg的学生大约为3 000×(0.03+0.05)×5=1 200(人),故B中结论正确;
对于C,体重在[55,70)内的频率为(0.03+0.05+0.06)×5=0.7,
体重在[55,75)内的频率为(0.03+0.05+0.06+0.04)×5=0.9,
故80%分位数在[70,75)内,设其为x,则0.7+0.04×(x-70)=0.8,得x=72.5,故C中结论正确;
对于D,样本数据的平均值为57.5×0.15+62.5×0.25+67.5×0.3+72.5×0.2+77.5×0.1=66.75,故D中结论正确.故选A.
5.C 样本空间Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)},共16个样本点,其中满足m≥n+1的样本点有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),共6个,故所求概率P=.
6.B 最后乙队获胜包含3种情况:(1)第三局乙胜;(2)第三局甲胜,第四局乙胜;(3)第三局和第四局都是甲胜,第五局乙胜.
故最后乙队获胜的概率P=,故选B.
7.A 由题意得,
=,
所以=1-a,又0所以0<,所以n8.B ①举反例:0,0,0,4,11,其平均数=3<4,但不符合入冬标准;
②假设有数据大于或等于10,由极差小于或等于3可知,该组数据中的最小值大于或等于7,此时数据的平均数必然大于7,与<4矛盾,假设错误,则此组数据全部小于10,符合入冬标准;
③举反例:1,1,1,1,11,其平均数=3<4,标准差s=4,但不符合入冬标准;
④当众数等于5且极差小于或等于4时,该组数据中最大的数不超过9,符合入冬标准.故选B.
9.ACD 事件C发生的频率为,因为只进行了一次试验,所以不能得出概率接近的结论,当然每抽10台电视机,必有1台次品也不一定发生.
10.ACD A选项,根据服务业商务活动指数折线图可知,2022年9月至12月服务业经济持续下降,所以A正确.
B选项,根据建筑业商务活动指数折线图可知,2022年9月至12月建筑业经济持续上升,所以B错误.
C选项,根据建筑业商务活动指数折线图可知,2022年5月建筑业经济上升幅度最小,所以C正确.
D选项,根据服务业商务活动指数折线图可知,2023年2月服务业经济上升幅度最大,所以D正确.
11.ACD 将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,所得四位数可能为1 111,1 115,1 151,1 155,1 511,1 515,1 551,1 555,5 111,5 115,5 151,5 155,5 511,5 515,5 551,5 555,共16个样本点.
事件A包含的样本点有1 155,1 515,1 551,5 115,5 151,5 511,共6个,因此P(A)=;
事件B包含的样本点有1 115,1 155,1 515,1 555,5 115,5 155,5 515,5 555,共8个,因此P(B)=;
事件A∪B包含的样本点有1 115,1 155,1 515,1 551,1 555,5 115,5 151,5 155,5 511,5 515,5 555,共11个,因此P(A∪B)=;
事件AB包含的样本点有1 155,1 515,5 115,共3个,因此P(AB)=.故选ACD.
12.答案 0.9
解析 因为P()=0.6,所以P(B)=1-P()=0.4.
因为三个事件A,B,C两两互斥,所以P(A∪B∪C)=P(A)+P(B)+P(C)=0.9.
13.答案 9
解析 甲的中位数为=18,乙的中位数为,
因为两组数据的中位数相等,所以=18,解得y=7,所以乙的平均值为=18,又两组数据的平均值相等,所以=18,解得x=2.所以x+y=9.
14.答案
解析 由题意得,恰好摸4次停止,说明前3次恰好只摸到1次红球,且第4次摸到红球,则其概率为.
设甲、乙两个袋子中的球的个数分别为a,3a,则甲袋中有个红球,乙袋中有3ap个红球.将甲、乙两个袋子中的球装在一起后,袋中共有4a个球,其中有个红球,则有,解得p=.
15.解析 (1)a==0.9,b=100×0.03×10×0.9=27.(2分)
因为年龄在[15,35)内的频率为(0.01+0.02)×10=0.3,在[15,45)内的频率为(0.01+0.02+0.03)×10=0.6,所以中位数在区间[35,45)内,(3分)
设中位数为x,则(x-35)×0.03=0.5-0.3,解得x≈42,
所以估计抽取的100人的年龄的中位数为42岁.(6分)
(2)由(1)可知第2、3、4组回答正确的共有18+27+9=54(人),(7分)
所以利用分层抽样的方法抽取6人,第2组抽取×6=2(人),记为m1,m2;第3组抽取×6=3(人),记为n1,n2,n3;第4组抽取×6=1(人),记为s.(10分)
该试验的样本空间Ω={m1m2,m1n1,m1n2,m1n3,m1s,m2n1,m2n2,m2n3,m2s,n1n2,n1n3,n1s,n2n3,n2s,n3s},
记事件M=“这2人都不在第2组”,则M={n1n2,n1n3,n1s,n2n3,n2s,n3s},(12分)
故P(M)=.(13分)
16.解析 (1)记事件A为甲胜乙,则P(A)=,
记事件B为甲胜丙,则P(B)=,
记事件C为乙胜丙,则P(C)=,(3分)
设前三场比赛结束后,丙被淘汰的概率为P1,
则P1=P(C.(5分)
(2)设只需四场比赛就决出冠军的概率为P2,
则P2=P(CBAB)
=.(10分)
(3)因为甲胜乙和甲胜丙的概率均为,且乙胜丙和丙胜乙的概率均为,第一场比赛甲当裁判,所以以后的比赛相对于甲而言,可将乙、丙视为同一人,设每一场比赛中甲胜为事件D,甲当裁判为事件E,甲最终获胜的概率为P3,则P(D)=.(15分)
17.解析 (1)由题中数据知四月前10天订单中百合花日需求量的众数为255枝,平均数×(231+241+243+244+251+252+255+255+263+265)=250(枝).(3分)
频率分布直方图如下:
(7分)
(2)设订单中百合花日需求量为a枝.
由(1)中频率分布直方图,知a的可能取值为235,245,255,265,相应频率分别为0.1,0.3,0.4,0.2,
则后20天中,a取235,245,255,265的天数分别为2,6,8,4.(9分)
若空运250枝,则当a=235时,当日利润为235×2-250×1.6=70(元),
当a=245时,当日利润为245×2-250×1.6=90(元),
当a=255时,当日利润为255×2-250×1.6-5×1.8=101(元),
当a=265时,当日利润为265×2-250×1.6-15×1.8=103(元),
故四月后20天百合花的销售总利润为70×2+90×6+101×8+103×4=1 900(元).(11分)
若空运255枝,则当a=235时,当日利润为235×2-255×1.6=62(元),
当a=245时,当日利润为245×2-255×1.6=82(元),
当a=255时,当日利润为255×2-255×1.6=102(元),
当a=265时,当日利润为265×2-255×1.6-10×1.8=104(元),
故四月后20天百合花的销售总利润为62×2+82×6+102×8+104×4=1 848(元).(13分)
因为1 900>1 848,所以微店每天从云南鲜花基地固定空运250枝百合花,四月后20天百合花的销售总利润更大.(15分)
18.解析 (1)设事件M,N分别表示A,B型备选电子元件正常工作,则P(M)=0.9,P(N)=0.8,且M,N相互独立.
所以电路子模块R不能正常工作的概率为P()=(1-0.9)×(1-0.8)=0.02,(4分)
因此电路子模块R能正常工作的概率为1-0.02=0.98.(6分)
(2)当1号位接入C型备选电子元件时,电路子模块Q能正常工作的概率最大.理由如下:
用事件D,E,F分别表示A,B,C型备选电子元件正常工作,则P(D)=0.7,P(E)=0.8,P(F)=0.9,且D,E,F相互独立.(9分)
若1号位元件为A型备选电子元件,则电路子模块Q能正常工作的概率为P(D)[1-P()]=P(D)[P(E)+P(F)-P(EF)]=0.7×(0.8+0.9-0.8×0.9)=0.686;(11分)
若1号位元件为B型备选电子元件,则电路子模块Q能正常工作的概率为P(E)[1-P()]=P(E)[P(D)+P(F)-P(DF)]=0.8×(0.7+0.9-0.7×0.9)=0.776;(13分)
若1号位元件为C型备选电子元件,则电路子模块Q能正常工作的概率为P(F)[1-P()]=P(F)[P(D)+P(E)-P(DE)]=0.9×(0.7+0.8-0.7×0.8)=0.846.(15分)
由于0.846>0.776>0.686,因此当1号位接入C型备选电子元件时,电路子模块Q能正常工作的概率最大.(17分)
19.解析 (1)①改进后,随机抽取的16件产品的评分(单位:分)依次变为
10.00 10.17 10.01 10.01 10.06 9.97 10.03 10.09
10.31 9.96 10.18 10.07 9.27 10.09 10.10 10.00
其中A等品有13件,所以估计改进后该生产线生产的产品中A等品所占的比例为.(4分)
②设未改进的生产线生产出的产品评分为yi(i=1,2,3,…,200)分,经过改进的生产线生产出的产品评分为zi(i=1,2,3,…,200)分,其中zi=yi+0.05.
用样本估计总体可知=9.97,
所以+0.05=10.02,(7分)
所以估计改进后该厂生产的所有产品评分的平均数为=9.995(分).(9分)
用样本估计总体可知≈0.045,
所以=0.045.(11分)
所以估计改进后该厂生产的所有产品评分的方差为
=
=0.045 625.(13分)
(2)将这1 500万元用于改进一条生产线,一年后因产品评分提高而增加的收益为(2 000-1 200)××200×365-1 500×104=325×104(元)=325(万元);将这1 500万元用于购买理财产品,一年后的收益为1 500×8.2%=123(万元).(16分)
因为325>123,所以将这1 500万元用于改进一条生产线,一年后的收益更大.(17分)
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第五章 统计与概率
全卷满分150分 考试用时120分钟
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.古代科举制度始于隋而成于唐,完备于宋,明代则是其发展的鼎盛阶段,其中表现之一为会试分南卷、北卷、中卷,并按比例录取,录取比例为11∶7∶2.若明宣德五年会试录取人数为100,则中卷录取人数为( )
A.10 B.15
C.30 D.35
2.某课外小组为了了解什么样的方式最能增强同学们进行垃圾分类的意识,随机对该校同学进行问卷调查,根据调查结果,得到如图所示的统计图,已知每个回答该问卷的同学都只能在问卷的五个选项中选择一个,则以下结论中错误的是( )
A.回答该问卷的总人数不可能是100
B.回答该问卷的同学中,选择“设置分类明确的垃圾桶”的人数最多
C.回答该问卷的同学中,选择“学校团委会宣传”的人数最少
D.回答该问卷的同学中,选择“播放公益广告”的比选择“学校要求”的少8人
3.抛掷一枚质地均匀的正方体骰子,观察向上一面的点数,则下列是互斥事件但不是对立事件的是( )
A.“大于3点”与“不大于3点” B.“大于3点”与“小于2点”
C.“大于3点”与“小于4点” D.“大于3点”与“小于5点”
4.为了加强对学生的营养健康监测,某校在3 000名学生中,抽查了100名学生的体重数据情况.根据所得数据绘制样本的频率分布直方图如图所示(同一组的数据用该组区间的中点值作代表),则下列结论不正确的是( )
A.样本数据的众数为65
B.该校学生中体重低于65 kg的学生大约为1 200人
C.样本数据的80%分位数为72.5
D.样本数据的平均值为66.75
5.一个袋中装有四个形状、大小完全相同的球,球的编号分别为1,2,3,4.先从袋中随机取一个球,记该球的编号为m,将球放回袋中,再从袋中随机取一个球,记该球的编号为n,则m≥n+1的概率为( )
A.
6.排球比赛的规则是5局3胜制(无平局),在某次排球比赛中,甲队在每局比赛中获胜的概率都相等,均为,前2局中乙队以2∶0领先,则最后乙队获胜的概率是( )
A.
7.已知x1,x2,…,xn的平均数为,y1,y2,…,ym的平均数为,且,若x1,x2,…,xn,y1,y2,…,ym的平均数,其中0
8.根据气象学上的标准,连续5天的日平均气温低于10 ℃即为入冬,某地将连续5天的日平均气温的记录数据(记录数据都是自然数)作为一组样本,现有4组样本①②③④,它们各自的数据特征如下:①平均数<4;②平均数<4且极差小于或等于3;③平均数<4且标准差s≤4;④众数等于5且极差小于或等于4.
则4组样本中一定符合入冬标准的有( )
A.1组 B.2组 C.3组 D.4组
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品,若用C表示抽到次品这一事件,则下列说法不正确的是( )
A.事件C发生的概率为 B.事件C发生的频率为
C.事件C发生的概率接近 D.每抽10台电视机,必有1台次品
10.下图为2022年2月至2023年2月建筑业和服务业的商务活动指数,该指数等于50%反映该行业经济与上月比较无变化,大于50%反映该行业经济比上月总体上升,小于50%反映该行业经济比上月总体下降,则下列说法正确的是( )
A.2022年9月至12月服务业经济持续下降
B.2022年9月至12月建筑业经济持续下降
C.2022年5月建筑业经济上升幅度最小
D.2023年2月服务业经济上升幅度最大
11.算盘是我国古代一项伟大的发明,是一类重要的计算工具.现有一把初始状态的算盘如图所示,自右向左,分别表示个位、十位、百位、千位等,上面一粒珠子(简称上珠)代表5,下面一粒珠子(简称下珠)代表1,五粒下珠表示的数的大小等于同组一粒上珠表示的数的大小.例如,个位拨动一粒上珠、十位拨动一粒下珠至梁上,表示数字15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,设事件A=“表示的四位数能被3整除”,B=“表示的四位数能被5整除”,则( )
A.P(A)=
C.P(A∪B)=
三、填空题(本题共3小题,每小题5分,共15分)
12.已知三个事件A,B,C两两互斥,且P(A)=0.3,P()=0.6,P(C)=0.2,则P(A∪B∪C)= .
13.如图所示的茎叶图记录了甲、乙两支篮球队各6名队员某场比赛的得分数据(单位:分).若这两组数据的中位数相等,且平均值也相等,则x+y= .
14.甲、乙两个袋子中分别装有若干个大小和质地均相同的红球和绿球,甲、乙两个袋子中的球的个数之比为1∶3,已知从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率为p.若从甲袋中有放回地摸球,每次摸出一个,直至第2次摸到红球即停止,则恰好摸4次停止的概率为 ;若将甲、乙两个袋子中的球装在一起后,从中摸出一个红球的概率是,则p的值为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)2023年东盟博览会于9月在南宁举办.某电视台对本市15~65岁的人群随机抽取100人,并按年龄段分成6组,绘制成如图所示的频率分布直方图.抽取的人需回答“2023年是第几届东盟博览会”的问题,回答问题的正确情况如表格所示.
组号 分组 回答正确的人数 回答正确的人数占本组的频率
第1组 [15,25) 5 0.5
第2组 [25,35) 18 a
第3组 [35,45) b 0.9
第4组 [45,55) 9 0.36
第5组 [55,65] 3 0.2
根据上述信息,解决下列问题:
(1)求表格中a,b的值,并估计抽取的100人的年龄的中位数(中位数的结果保留整数);
(2)从第2、3、4组回答正确的人中用分层抽样的方法抽取6人,并从这6人中随机抽取2人,求这2人都不在第2组的概率.
16.(15分)甲、乙、丙三人进行摔跤比赛,比赛规则如下:①每场比赛有两人参加,另一人当裁判,没有平局;②每场比赛结束时,负的一方在下一场当裁判;③累计负两场者被淘汰;④当一人被淘汰后,剩余的两人继续比赛,直至其中一人累计负两场被淘汰,另一人最终获得冠军,比赛结束.已知在每场比赛中,甲胜乙和甲胜丙的概率均为,乙胜丙的概率为,各局比赛的结果相互独立.经抽签,第一场比赛甲当裁判.
(1)求前三场比赛结束后,丙被淘汰的概率;
(2)求只需四场比赛就决出冠军的概率;
(3)求甲最终获胜的概率.
17.(15分)有一家经销鲜花产品的微店,为保障售出的百合花的品质,每天从云南鲜花基地空运固定数量的百合花,若有剩余,则免费分赠给第二天购花的顾客,若不足,则从本地鲜花供应商处进货.某年四月前10天,微店百合花的售价为每枝2元,从云南空运来的百合花每枝进价为1.6元,本地供应商处的百合花每枝进价为1.8元.微店这10天的订单中百合花的日需求量(单位:枝)依次为251,255,231,243,263,241,265,255,244,252.
(1)求该年四月前10天订单中百合花日需求量的平均数和众数,并完成频率分布直方图;
(2)预计该年四月的后20天的订单中,百合花日需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(1)中频率分布直方图判断微店每天从云南鲜花基地固定空运250枝,还是255枝百合花,四月后20天百合花的销售总利润更大(同一组中的需求量数据用该组区间的中点值作代表,各区间的概率用该区间的频率代替).
18.(17分)某企业生产两种电路子模块R,Q,如图所示.要求在每个模块中,不同位置接入不同类型的电子元件,且备选电子元件为A,B,C型.假设不同位置的元件是否正常工作不受其他元件影响.在电路子模块R中,当1号位与2号位元件中至少有一个正常工作时,电路子模块才能正常工作;在电路子模块Q中,当1号位元件正常工作,且2号位与3号位元件中至少有一个正常工作时,电路子模块才能正常工作.
(1)若A,B型备选电子元件正常工作的概率分别为0.9,0.8,依次接入位置1,2,求此时电路子模块R能正常工作的概率;
(2)若A,B,C型备选电子元件正常工作的概率分别为0.7,0.8,0.9,如何接入备选电子元件,电路子模块Q能正常工作的概率最大 并说明理由.
19.(17分)某玻璃工艺品加工厂有2条生产线用于生产某款产品,每条生产线一天能生产200件该产品,该产品市场评级规定:评分在10分及以上的为A等品,低于10分的为B等品.厂家将A等品售价定为2 000元/件,B等品售价定为1 200元/件.下面是检验员在现有生产线上随机抽取的16件产品的评分(单位:分):
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得≈0.045,其中xi为抽取的第i件产品的评分(单位:分),i=1,2,…,16.
该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费1 500万元,改进后该条生产线产能不变,但生产出的每件产品的评分均提高0.05分,已知该厂现有1 500万元的资金.
(1)若厂家用这1 500万元改进一条生产线,根据随机抽取的16件产品的评分,估计:
①改进后该生产线生产的产品中A等品所占的比例;
②改进后该厂生产的所有产品评分的平均数和方差;
(2)某金融机构向该厂推销一款年收益率为8.2%的理财产品,请你利用所学知识分析,将这1 500万元用于购买该款理财产品所获得的收益与用于改进一条生产线使产品评分提高所增加的收益相比,一年后哪种方案的收益更大.(一年按365天计算)
答案与解析
第五章 统计与概率
1.A 2.D 3.B 4.A 5.C 6.B
7.A 8.B 9.ACD 10.ACD 11.ACD
1.A 依题意知,中卷录取人数为100×=10.
2.D 根据题意,当回答该问卷的总人数为100时,选择③④的同学人数不是整数,所以总人数不可能是100,故A中结论正确;
从题中统计图可得回答该问卷的同学中,选择⑤的人数最多,选择③的人数最少,故B、C中结论正确;
回答该问卷的同学中,选择“播放公益广告”的人数比选择“学校要求”的人数少8%,故D中结论错误.
3.B 对于A,事件“大于3点”指“点数为4或5或6”,事件“不大于3点”指“点数为1或2或3”,
所以事件“大于3点”与“不大于3点”不可能同时发生,且两事件的和事件为必然事件,所以事件“大于3点”与事件“不大于3点”是互斥事件,且是对立事件,A错误;
对于B,事件“小于2点”指“点数为1”,所以事件“大于3点”与“小于2点”不可能同时发生,但它们的和事件不是必然事件,所以事件“大于3点”与事件“小于2点”为互斥事件,但不是对立事件,B正确;
对于C,事件“小于4点”指“点数为1或2或3”,
所以事件“大于3点”与“小于4点”不可能同时发生,且两事件的和事件为必然事件,所以事件“大于3点”与事件“小于4点”是互斥事件,且是对立事件,C错误;
对于D,事件“小于5点”指“点数为1或2或3或4”,
所以事件“大于3点”与“小于5点”可能同时发生,
所以事件“大于3点”与事件“小于5点”不是互斥事件,D错误.故选B.
4.A 对于A,样本数据的众数为67.5,故A中结论错误;
对于B,该校学生中低于65 kg的学生大约为3 000×(0.03+0.05)×5=1 200(人),故B中结论正确;
对于C,体重在[55,70)内的频率为(0.03+0.05+0.06)×5=0.7,
体重在[55,75)内的频率为(0.03+0.05+0.06+0.04)×5=0.9,
故80%分位数在[70,75)内,设其为x,则0.7+0.04×(x-70)=0.8,得x=72.5,故C中结论正确;
对于D,样本数据的平均值为57.5×0.15+62.5×0.25+67.5×0.3+72.5×0.2+77.5×0.1=66.75,故D中结论正确.故选A.
5.C 样本空间Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)},共16个样本点,其中满足m≥n+1的样本点有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),共6个,故所求概率P=.
6.B 最后乙队获胜包含3种情况:(1)第三局乙胜;(2)第三局甲胜,第四局乙胜;(3)第三局和第四局都是甲胜,第五局乙胜.
故最后乙队获胜的概率P=,故选B.
7.A 由题意得,
=,
所以=1-a,又0
②假设有数据大于或等于10,由极差小于或等于3可知,该组数据中的最小值大于或等于7,此时数据的平均数必然大于7,与<4矛盾,假设错误,则此组数据全部小于10,符合入冬标准;
③举反例:1,1,1,1,11,其平均数=3<4,标准差s=4,但不符合入冬标准;
④当众数等于5且极差小于或等于4时,该组数据中最大的数不超过9,符合入冬标准.故选B.
9.ACD 事件C发生的频率为,因为只进行了一次试验,所以不能得出概率接近的结论,当然每抽10台电视机,必有1台次品也不一定发生.
10.ACD A选项,根据服务业商务活动指数折线图可知,2022年9月至12月服务业经济持续下降,所以A正确.
B选项,根据建筑业商务活动指数折线图可知,2022年9月至12月建筑业经济持续上升,所以B错误.
C选项,根据建筑业商务活动指数折线图可知,2022年5月建筑业经济上升幅度最小,所以C正确.
D选项,根据服务业商务活动指数折线图可知,2023年2月服务业经济上升幅度最大,所以D正确.
11.ACD 将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,所得四位数可能为1 111,1 115,1 151,1 155,1 511,1 515,1 551,1 555,5 111,5 115,5 151,5 155,5 511,5 515,5 551,5 555,共16个样本点.
事件A包含的样本点有1 155,1 515,1 551,5 115,5 151,5 511,共6个,因此P(A)=;
事件B包含的样本点有1 115,1 155,1 515,1 555,5 115,5 155,5 515,5 555,共8个,因此P(B)=;
事件A∪B包含的样本点有1 115,1 155,1 515,1 551,1 555,5 115,5 151,5 155,5 511,5 515,5 555,共11个,因此P(A∪B)=;
事件AB包含的样本点有1 155,1 515,5 115,共3个,因此P(AB)=.故选ACD.
12.答案 0.9
解析 因为P()=0.6,所以P(B)=1-P()=0.4.
因为三个事件A,B,C两两互斥,所以P(A∪B∪C)=P(A)+P(B)+P(C)=0.9.
13.答案 9
解析 甲的中位数为=18,乙的中位数为,
因为两组数据的中位数相等,所以=18,解得y=7,所以乙的平均值为=18,又两组数据的平均值相等,所以=18,解得x=2.所以x+y=9.
14.答案
解析 由题意得,恰好摸4次停止,说明前3次恰好只摸到1次红球,且第4次摸到红球,则其概率为.
设甲、乙两个袋子中的球的个数分别为a,3a,则甲袋中有个红球,乙袋中有3ap个红球.将甲、乙两个袋子中的球装在一起后,袋中共有4a个球,其中有个红球,则有,解得p=.
15.解析 (1)a==0.9,b=100×0.03×10×0.9=27.(2分)
因为年龄在[15,35)内的频率为(0.01+0.02)×10=0.3,在[15,45)内的频率为(0.01+0.02+0.03)×10=0.6,所以中位数在区间[35,45)内,(3分)
设中位数为x,则(x-35)×0.03=0.5-0.3,解得x≈42,
所以估计抽取的100人的年龄的中位数为42岁.(6分)
(2)由(1)可知第2、3、4组回答正确的共有18+27+9=54(人),(7分)
所以利用分层抽样的方法抽取6人,第2组抽取×6=2(人),记为m1,m2;第3组抽取×6=3(人),记为n1,n2,n3;第4组抽取×6=1(人),记为s.(10分)
该试验的样本空间Ω={m1m2,m1n1,m1n2,m1n3,m1s,m2n1,m2n2,m2n3,m2s,n1n2,n1n3,n1s,n2n3,n2s,n3s},
记事件M=“这2人都不在第2组”,则M={n1n2,n1n3,n1s,n2n3,n2s,n3s},(12分)
故P(M)=.(13分)
16.解析 (1)记事件A为甲胜乙,则P(A)=,
记事件B为甲胜丙,则P(B)=,
记事件C为乙胜丙,则P(C)=,(3分)
设前三场比赛结束后,丙被淘汰的概率为P1,
则P1=P(C.(5分)
(2)设只需四场比赛就决出冠军的概率为P2,
则P2=P(CBAB)
=.(10分)
(3)因为甲胜乙和甲胜丙的概率均为,且乙胜丙和丙胜乙的概率均为,第一场比赛甲当裁判,所以以后的比赛相对于甲而言,可将乙、丙视为同一人,设每一场比赛中甲胜为事件D,甲当裁判为事件E,甲最终获胜的概率为P3,则P(D)=.(15分)
17.解析 (1)由题中数据知四月前10天订单中百合花日需求量的众数为255枝,平均数×(231+241+243+244+251+252+255+255+263+265)=250(枝).(3分)
频率分布直方图如下:
(7分)
(2)设订单中百合花日需求量为a枝.
由(1)中频率分布直方图,知a的可能取值为235,245,255,265,相应频率分别为0.1,0.3,0.4,0.2,
则后20天中,a取235,245,255,265的天数分别为2,6,8,4.(9分)
若空运250枝,则当a=235时,当日利润为235×2-250×1.6=70(元),
当a=245时,当日利润为245×2-250×1.6=90(元),
当a=255时,当日利润为255×2-250×1.6-5×1.8=101(元),
当a=265时,当日利润为265×2-250×1.6-15×1.8=103(元),
故四月后20天百合花的销售总利润为70×2+90×6+101×8+103×4=1 900(元).(11分)
若空运255枝,则当a=235时,当日利润为235×2-255×1.6=62(元),
当a=245时,当日利润为245×2-255×1.6=82(元),
当a=255时,当日利润为255×2-255×1.6=102(元),
当a=265时,当日利润为265×2-255×1.6-10×1.8=104(元),
故四月后20天百合花的销售总利润为62×2+82×6+102×8+104×4=1 848(元).(13分)
因为1 900>1 848,所以微店每天从云南鲜花基地固定空运250枝百合花,四月后20天百合花的销售总利润更大.(15分)
18.解析 (1)设事件M,N分别表示A,B型备选电子元件正常工作,则P(M)=0.9,P(N)=0.8,且M,N相互独立.
所以电路子模块R不能正常工作的概率为P()=(1-0.9)×(1-0.8)=0.02,(4分)
因此电路子模块R能正常工作的概率为1-0.02=0.98.(6分)
(2)当1号位接入C型备选电子元件时,电路子模块Q能正常工作的概率最大.理由如下:
用事件D,E,F分别表示A,B,C型备选电子元件正常工作,则P(D)=0.7,P(E)=0.8,P(F)=0.9,且D,E,F相互独立.(9分)
若1号位元件为A型备选电子元件,则电路子模块Q能正常工作的概率为P(D)[1-P()]=P(D)[P(E)+P(F)-P(EF)]=0.7×(0.8+0.9-0.8×0.9)=0.686;(11分)
若1号位元件为B型备选电子元件,则电路子模块Q能正常工作的概率为P(E)[1-P()]=P(E)[P(D)+P(F)-P(DF)]=0.8×(0.7+0.9-0.7×0.9)=0.776;(13分)
若1号位元件为C型备选电子元件,则电路子模块Q能正常工作的概率为P(F)[1-P()]=P(F)[P(D)+P(E)-P(DE)]=0.9×(0.7+0.8-0.7×0.8)=0.846.(15分)
由于0.846>0.776>0.686,因此当1号位接入C型备选电子元件时,电路子模块Q能正常工作的概率最大.(17分)
19.解析 (1)①改进后,随机抽取的16件产品的评分(单位:分)依次变为
10.00 10.17 10.01 10.01 10.06 9.97 10.03 10.09
10.31 9.96 10.18 10.07 9.27 10.09 10.10 10.00
其中A等品有13件,所以估计改进后该生产线生产的产品中A等品所占的比例为.(4分)
②设未改进的生产线生产出的产品评分为yi(i=1,2,3,…,200)分,经过改进的生产线生产出的产品评分为zi(i=1,2,3,…,200)分,其中zi=yi+0.05.
用样本估计总体可知=9.97,
所以+0.05=10.02,(7分)
所以估计改进后该厂生产的所有产品评分的平均数为=9.995(分).(9分)
用样本估计总体可知≈0.045,
所以=0.045.(11分)
所以估计改进后该厂生产的所有产品评分的方差为
=
=0.045 625.(13分)
(2)将这1 500万元用于改进一条生产线,一年后因产品评分提高而增加的收益为(2 000-1 200)××200×365-1 500×104=325×104(元)=325(万元);将这1 500万元用于购买理财产品,一年后的收益为1 500×8.2%=123(万元).(16分)
因为325>123,所以将这1 500万元用于改进一条生产线,一年后的收益更大.(17分)
