华师七上1.6.1有理数的加法法则 课件(共28张PPT)
文档属性
| 名称 | 华师七上1.6.1有理数的加法法则 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 874.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 08:36:15 | ||
图片预览






文档简介
(共28张PPT)
(华师大版)七年级
上
1.6.1有理数的加法法则
有理数
第1章
“—”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
内容总览
目录
教学目标
1.通过借助数轴理解有理数加法的意义,体会数形结合的思想方法.
2.掌握有理数加法法则,能熟练进行有理数的加法运算,提高运算能力.
新知导入
魏晋时期的数学家刘徽在其著作《九章算术注》中用不同颜色的算筹 (小棍形状的记数工作) 分别表示正数和负数 (红色为正,黑色为负). 你能写出下列算筹表示的数和最终结果吗?
( ) + ( ) =
+2
-4
请思考有负数的加法如何计算?
问题:小明在一条东西向的跑道上,先走了20m,又走了30m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米
新知讲解
我们知道,求两次运动的总结果,可以用加法来解答.可是上述问题不能得到确定的答案,因为小明最后所在的位置与行走方向有关.
探索:
不妨规定向东为正,向西为负.
(1)若两次都是向东走,很明显,一共向东走了50m.
写成算式是:(+20) +(+30)=+50,
即小明位于原来位置的东边50m处.
这一运算过程在数轴上可表示为下图.
新知讲解
0
10
20
30
40
50
20
30
50
东
西
-10
探索:
不妨规定向东为正,向西为负.
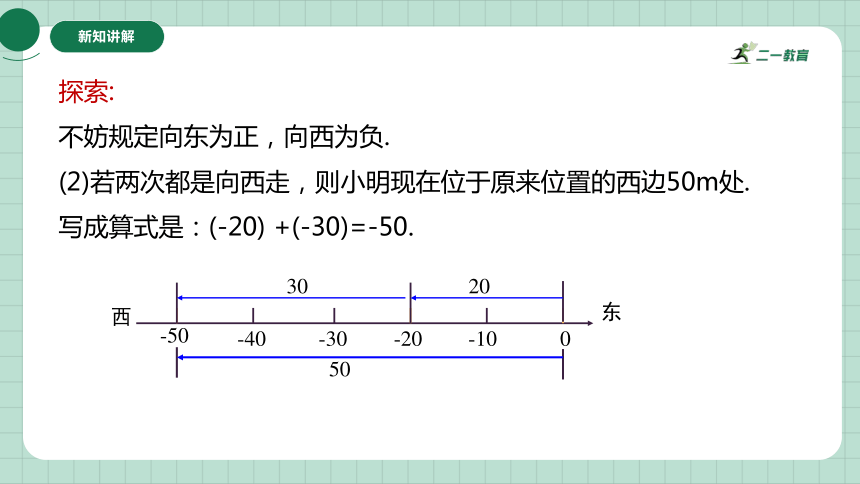
(2)若两次都是向西走,则小明现在位于原来位置的西边50m处.
写成算式是:(-20) +(-30)=-50.
新知讲解
-10
0
-20
-30
-40
-50
20
30
50
东
西
新知讲解
(+20)+(+30)= +(20+30)=+50
(- 20)+(-30)= -(20+30)= -50
加数
加数
和
观察上面两个式子,你发现了什么?
同号两数相加,取与加数相同的正负号,并把绝对值相加;
有理数的加法法则一
探索:
不妨规定向东为正,向西为负.
(3)若第一次向东起20m,第二次向西走30m.在数轴上.我们可以看到,小明位于原来位置的西边10m处.
新知讲解
东
-10
10
30
20
-20
0
20
30
10
(+20)+(-30)=-10
西
探索:
不妨规定向东为正,向西为负.
(4)先向西走20米,再向东走30米.
新知讲解
东
-10
10
30
20
-20
0
20
30
10
(-20)+(+30)= +10
西
后两种情形中两个加数的正负号不同(通常可称为异号),让我们再试几次(下列算式中,各个加数的正负号和绝对值仍分别表示运动的方向和路程) :
新知讲解
(+4) +(-3)=( ),
(+3) +(- 10)=( ),
(-5) +(+7)=( ),
(-6) +2=( ).
+1
-7
+2
-4
新知讲解
(+20) +(-30)=-(30-20)=-10.
(-20) +(+30)=+(30-20)=+10.
加数
加数
和
观察上面两个式子,你发现了什么?
绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值.
有理数的加法法则二
探索:
不妨规定向东为正,向西为负.
还有两种特殊情形:
第一次向西走了30m,第二次向东走了30m.
写成算式是:(-30) +(+30)=( );
新知讲解
0
互为相反数的两个数相加得0.
有理数的加法法则三
探索:
不妨规定向东为正,向西为负.
还有两种特殊情形:
第一次向西走了30m,第二次没走,
写成算式是:(-30) +0=( ).
新知讲解
-30
一个数与0相加,仍得这个数 .
有理数的加法法则四
新知讲解
有理数的加法法则:
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数 .
这里从运算角度反映了相反数的一个特性.
新知讲解
注意:
一个有理数由正负号和绝对值两部分组成,进行加法运算时,应注意先确定和的正负号,再确定绝对值.
例1 计算:
(1)(+2)+(-11); (2)(-12)+(+12);
(3)(-)+(-); (4)(-3.4)+4.3 .
新知讲解
解:(1)(+2)+ (-11)=-(11-2)=-9.
(2) (-12) +(+12)=0.
(3)(-)+(-)=-(+)=-1;
(4)(-3.4)+4.3=+(4.3-3.4)=0.9.
依据有理数加法法则二
依据有理数加法法则三
依据有理数加法法则一
依据有理数加法法则二
有理数的加法法则,还可以帮助我们进一步理解相反数的意义,它告诉我们:两个数互为相反数的特征是这两个数的和为0.
新知讲解
一方面,由法则3,如果两个数a、b互为相反数,那么a+b=0;
另一方面,如果a+b=0,那么a、b互为相反数.
这是因为,如果a、6不互为相反数,那么无论它们是同号、异号(绝对值不相等)还是只有一个数为0,由法则1、2、4知,它们的和都不可能为0.
新知讲解
有理数加法的运算步骤:
1.先判断类型 (同号、异号等);
2.再确定和的正负号;
3.最后确定和的绝对值.
课堂练习
基础题
1.下列运算正确的是( )
A.(-2)+(-2)=0 B.(-6)+(+4)=-10
C.(+12)+(+3)=-15 D.(+21)+(-2)=19
2.有下列说法:①若两个加数都是正数,其和一定为正数;
②若两个数的和是正数,则这两个加数一定都为正数;
③若两个加数都是负数,其和一定为负数;
④若两个数的和是负数,则这两个加数一定都为负数.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
D
C
课堂练习
基础题
3.已知=8,=3,a<b,则a+b=_________.
-5或-11
(1) (-0.6)+(-2.7); (2) 3.7+(-8.4);
(3) 3.22+1.78; (4) 7+(-3.3);
(5) 0+(-5.8); (6) 2025+(-2025).
4. 计算:
解:(1) (-0.6)+(-2.7)=-(0.6+2.7)=-3.3.
(2) 3.7+(-8.4)=-(8.4-3.7)=-4.7.
(3) 3.22+1.78=+(3.22+1.78)=5.
(4) 7+(-3.3)=+(7-3.3)=3.7.
课堂练习
1.若知有理数a,b,c在数轴上的位置如图所示,则下列结论中错误的是( )
A. a+b<0 B. b+c<0 C. a+b+c<0 D. |a+b|=a+b
D
a
c
0
b
提升题
课堂练习
提升题
2.已知[x]表示不超过x的最大整数.如:[3.2]=3,[﹣0.7]=﹣1.
现定义:{x}=[x]﹣x,如{1.5}=[1.5]﹣1.5=﹣0.5,则{3.9}+{﹣}=_______.
-1.4
课堂练习
拓展题
|(+4)+(+7)| |+4|+|+7|;
|(-4)+(-7)| |-4|+|-7|;
|(+4)+(-7)| |+4|+|-7|;
|0+(-7)| 0+|-7|;
(2)做完上述这组填空题,你可以得出什么结论?请用字母表述你的结论.
解:(2)两个有理数和的绝对值小于或等于这两个数的绝对值的和,用字母表示+ b |≤| a |+| b |( a , b 为有理数).
=
=
<
=
解:(2)两个有理数和的绝对值小于或等于这两个数的绝对值的和,
用字母表示为| a + b |≤| a |+| b |( a , b 为有理数).
(新考法)(1)试用“>”“<”或“=”填空:
课堂总结
有理数的加法法则:
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数 .
板书设计
有理数的加法法则:
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数 .
课题:1.6.1有理数的加法法则
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
上
1.6.1有理数的加法法则
有理数
第1章
“—”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
内容总览
目录
教学目标
1.通过借助数轴理解有理数加法的意义,体会数形结合的思想方法.
2.掌握有理数加法法则,能熟练进行有理数的加法运算,提高运算能力.
新知导入
魏晋时期的数学家刘徽在其著作《九章算术注》中用不同颜色的算筹 (小棍形状的记数工作) 分别表示正数和负数 (红色为正,黑色为负). 你能写出下列算筹表示的数和最终结果吗?
( ) + ( ) =
+2
-4
请思考有负数的加法如何计算?
问题:小明在一条东西向的跑道上,先走了20m,又走了30m,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米
新知讲解
我们知道,求两次运动的总结果,可以用加法来解答.可是上述问题不能得到确定的答案,因为小明最后所在的位置与行走方向有关.
探索:
不妨规定向东为正,向西为负.
(1)若两次都是向东走,很明显,一共向东走了50m.
写成算式是:(+20) +(+30)=+50,
即小明位于原来位置的东边50m处.
这一运算过程在数轴上可表示为下图.
新知讲解
0
10
20
30
40
50
20
30
50
东
西
-10
探索:
不妨规定向东为正,向西为负.
(2)若两次都是向西走,则小明现在位于原来位置的西边50m处.
写成算式是:(-20) +(-30)=-50.
新知讲解
-10
0
-20
-30
-40
-50
20
30
50
东
西
新知讲解
(+20)+(+30)= +(20+30)=+50
(- 20)+(-30)= -(20+30)= -50
加数
加数
和
观察上面两个式子,你发现了什么?
同号两数相加,取与加数相同的正负号,并把绝对值相加;
有理数的加法法则一
探索:
不妨规定向东为正,向西为负.
(3)若第一次向东起20m,第二次向西走30m.在数轴上.我们可以看到,小明位于原来位置的西边10m处.
新知讲解
东
-10
10
30
20
-20
0
20
30
10
(+20)+(-30)=-10
西
探索:
不妨规定向东为正,向西为负.
(4)先向西走20米,再向东走30米.
新知讲解
东
-10
10
30
20
-20
0
20
30
10
(-20)+(+30)= +10
西
后两种情形中两个加数的正负号不同(通常可称为异号),让我们再试几次(下列算式中,各个加数的正负号和绝对值仍分别表示运动的方向和路程) :
新知讲解
(+4) +(-3)=( ),
(+3) +(- 10)=( ),
(-5) +(+7)=( ),
(-6) +2=( ).
+1
-7
+2
-4
新知讲解
(+20) +(-30)=-(30-20)=-10.
(-20) +(+30)=+(30-20)=+10.
加数
加数
和
观察上面两个式子,你发现了什么?
绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值.
有理数的加法法则二
探索:
不妨规定向东为正,向西为负.
还有两种特殊情形:
第一次向西走了30m,第二次向东走了30m.
写成算式是:(-30) +(+30)=( );
新知讲解
0
互为相反数的两个数相加得0.
有理数的加法法则三
探索:
不妨规定向东为正,向西为负.
还有两种特殊情形:
第一次向西走了30m,第二次没走,
写成算式是:(-30) +0=( ).
新知讲解
-30
一个数与0相加,仍得这个数 .
有理数的加法法则四
新知讲解
有理数的加法法则:
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数 .
这里从运算角度反映了相反数的一个特性.
新知讲解
注意:
一个有理数由正负号和绝对值两部分组成,进行加法运算时,应注意先确定和的正负号,再确定绝对值.
例1 计算:
(1)(+2)+(-11); (2)(-12)+(+12);
(3)(-)+(-); (4)(-3.4)+4.3 .
新知讲解
解:(1)(+2)+ (-11)=-(11-2)=-9.
(2) (-12) +(+12)=0.
(3)(-)+(-)=-(+)=-1;
(4)(-3.4)+4.3=+(4.3-3.4)=0.9.
依据有理数加法法则二
依据有理数加法法则三
依据有理数加法法则一
依据有理数加法法则二
有理数的加法法则,还可以帮助我们进一步理解相反数的意义,它告诉我们:两个数互为相反数的特征是这两个数的和为0.
新知讲解
一方面,由法则3,如果两个数a、b互为相反数,那么a+b=0;
另一方面,如果a+b=0,那么a、b互为相反数.
这是因为,如果a、6不互为相反数,那么无论它们是同号、异号(绝对值不相等)还是只有一个数为0,由法则1、2、4知,它们的和都不可能为0.
新知讲解
有理数加法的运算步骤:
1.先判断类型 (同号、异号等);
2.再确定和的正负号;
3.最后确定和的绝对值.
课堂练习
基础题
1.下列运算正确的是( )
A.(-2)+(-2)=0 B.(-6)+(+4)=-10
C.(+12)+(+3)=-15 D.(+21)+(-2)=19
2.有下列说法:①若两个加数都是正数,其和一定为正数;
②若两个数的和是正数,则这两个加数一定都为正数;
③若两个加数都是负数,其和一定为负数;
④若两个数的和是负数,则这两个加数一定都为负数.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
D
C
课堂练习
基础题
3.已知=8,=3,a<b,则a+b=_________.
-5或-11
(1) (-0.6)+(-2.7); (2) 3.7+(-8.4);
(3) 3.22+1.78; (4) 7+(-3.3);
(5) 0+(-5.8); (6) 2025+(-2025).
4. 计算:
解:(1) (-0.6)+(-2.7)=-(0.6+2.7)=-3.3.
(2) 3.7+(-8.4)=-(8.4-3.7)=-4.7.
(3) 3.22+1.78=+(3.22+1.78)=5.
(4) 7+(-3.3)=+(7-3.3)=3.7.
课堂练习
1.若知有理数a,b,c在数轴上的位置如图所示,则下列结论中错误的是( )
A. a+b<0 B. b+c<0 C. a+b+c<0 D. |a+b|=a+b
D
a
c
0
b
提升题
课堂练习
提升题
2.已知[x]表示不超过x的最大整数.如:[3.2]=3,[﹣0.7]=﹣1.
现定义:{x}=[x]﹣x,如{1.5}=[1.5]﹣1.5=﹣0.5,则{3.9}+{﹣}=_______.
-1.4
课堂练习
拓展题
|(+4)+(+7)| |+4|+|+7|;
|(-4)+(-7)| |-4|+|-7|;
|(+4)+(-7)| |+4|+|-7|;
|0+(-7)| 0+|-7|;
(2)做完上述这组填空题,你可以得出什么结论?请用字母表述你的结论.
解:(2)两个有理数和的绝对值小于或等于这两个数的绝对值的和,用字母表示+ b |≤| a |+| b |( a , b 为有理数).
=
=
<
=
解:(2)两个有理数和的绝对值小于或等于这两个数的绝对值的和,
用字母表示为| a + b |≤| a |+| b |( a , b 为有理数).
(新考法)(1)试用“>”“<”或“=”填空:
课堂总结
有理数的加法法则:
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数 .
板书设计
有理数的加法法则:
1.同号两数相加,取与加数相同的正负号,并把绝对值相加;
2.绝对值不相等的异号两数相加,取绝对值较大的加数的正负号,并用较大的绝对值减去较小的绝对值;
3.互为相反数的两个数相加得0;
4.一个数与0相加,仍得这个数 .
课题:1.6.1有理数的加法法则
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
